Study on OTFS Fractional Doppler Channel Estimation and Windowing in High-Speed Mobile Communication Systems
-
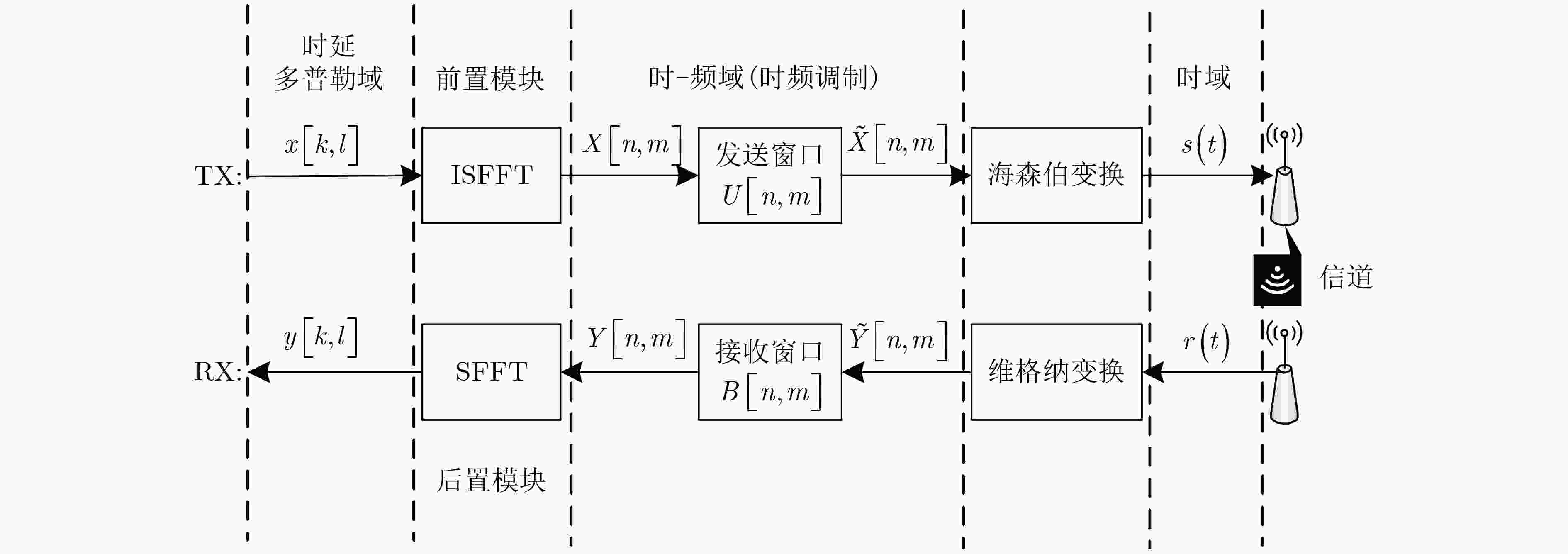
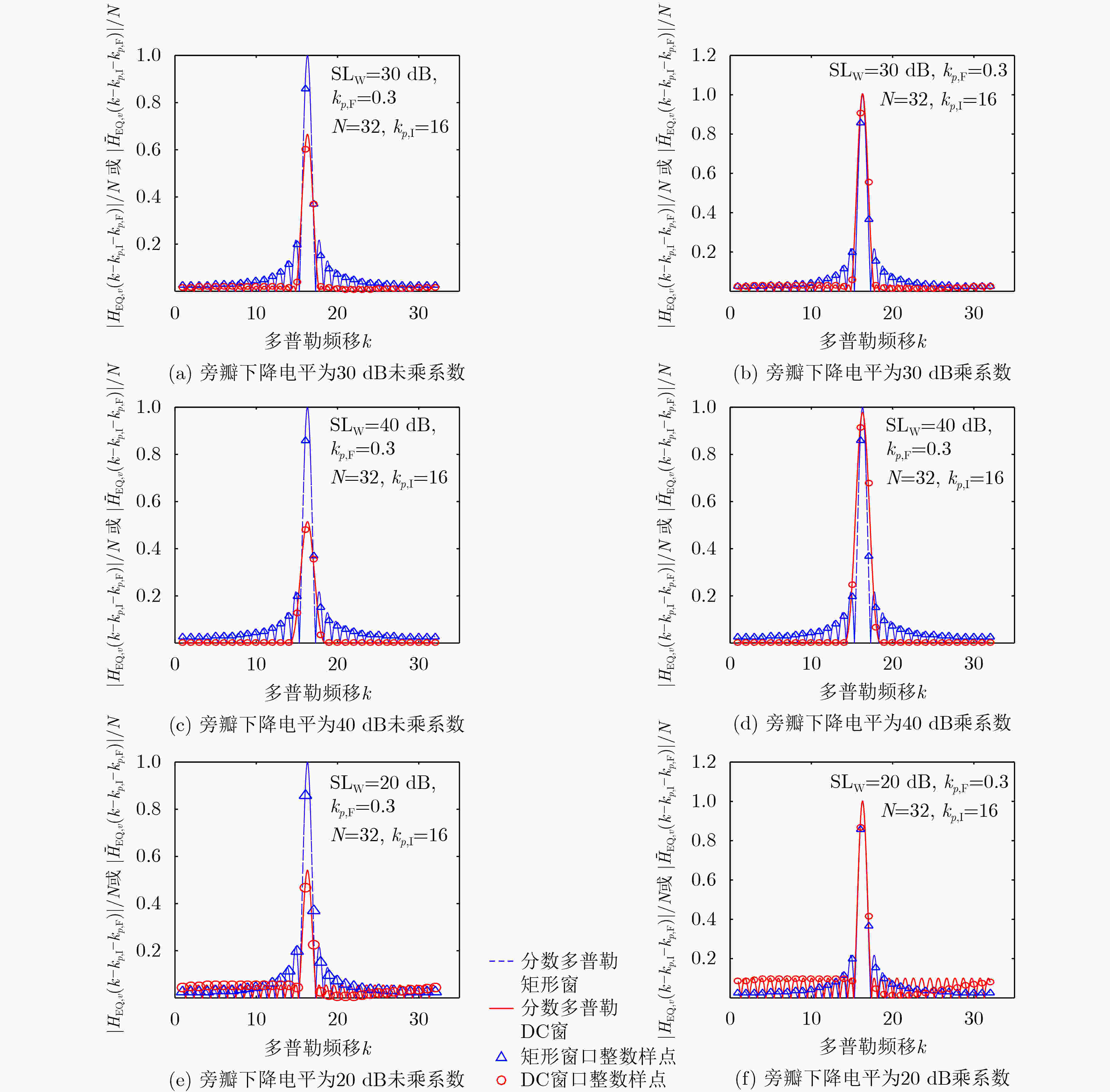
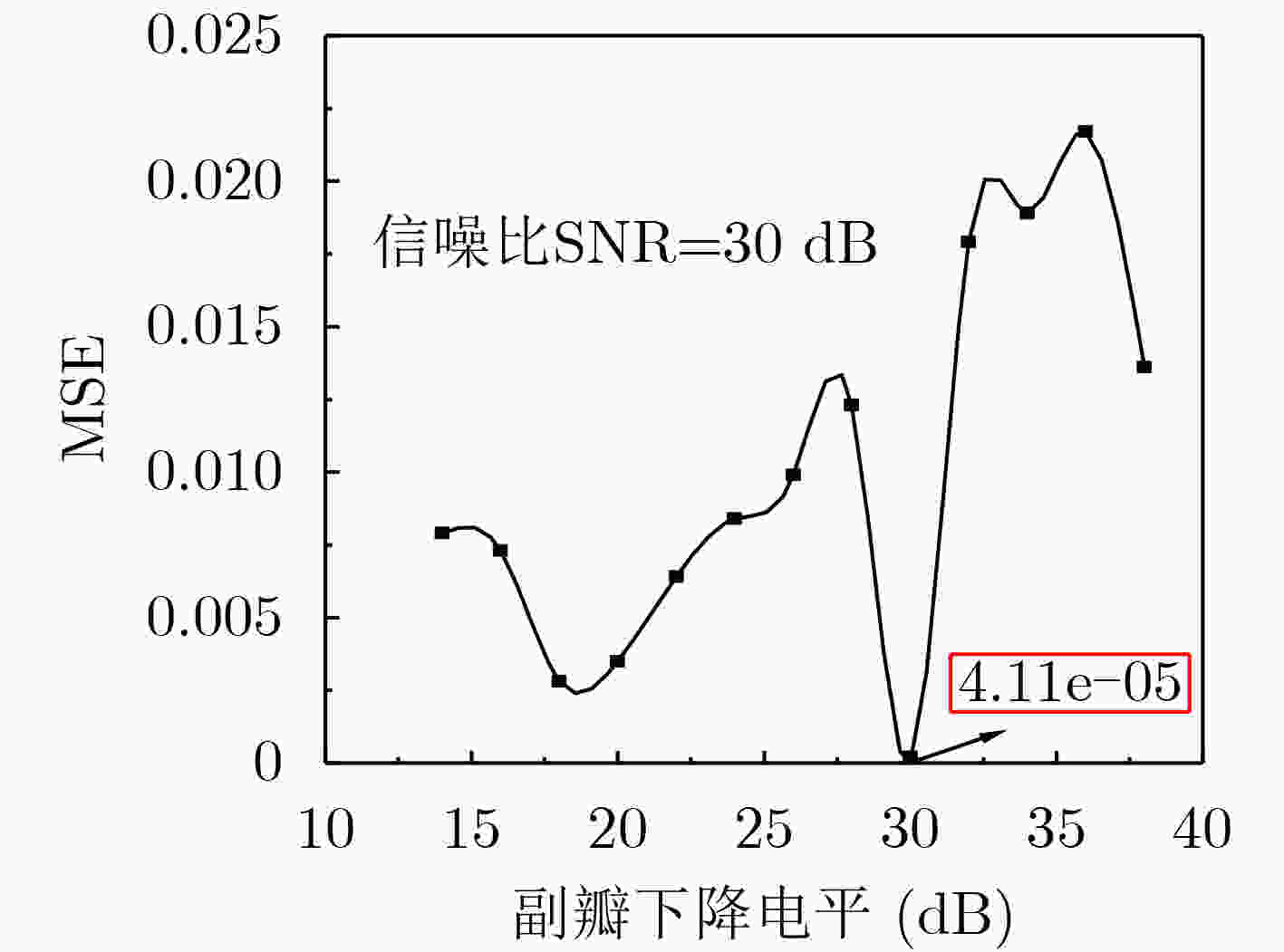
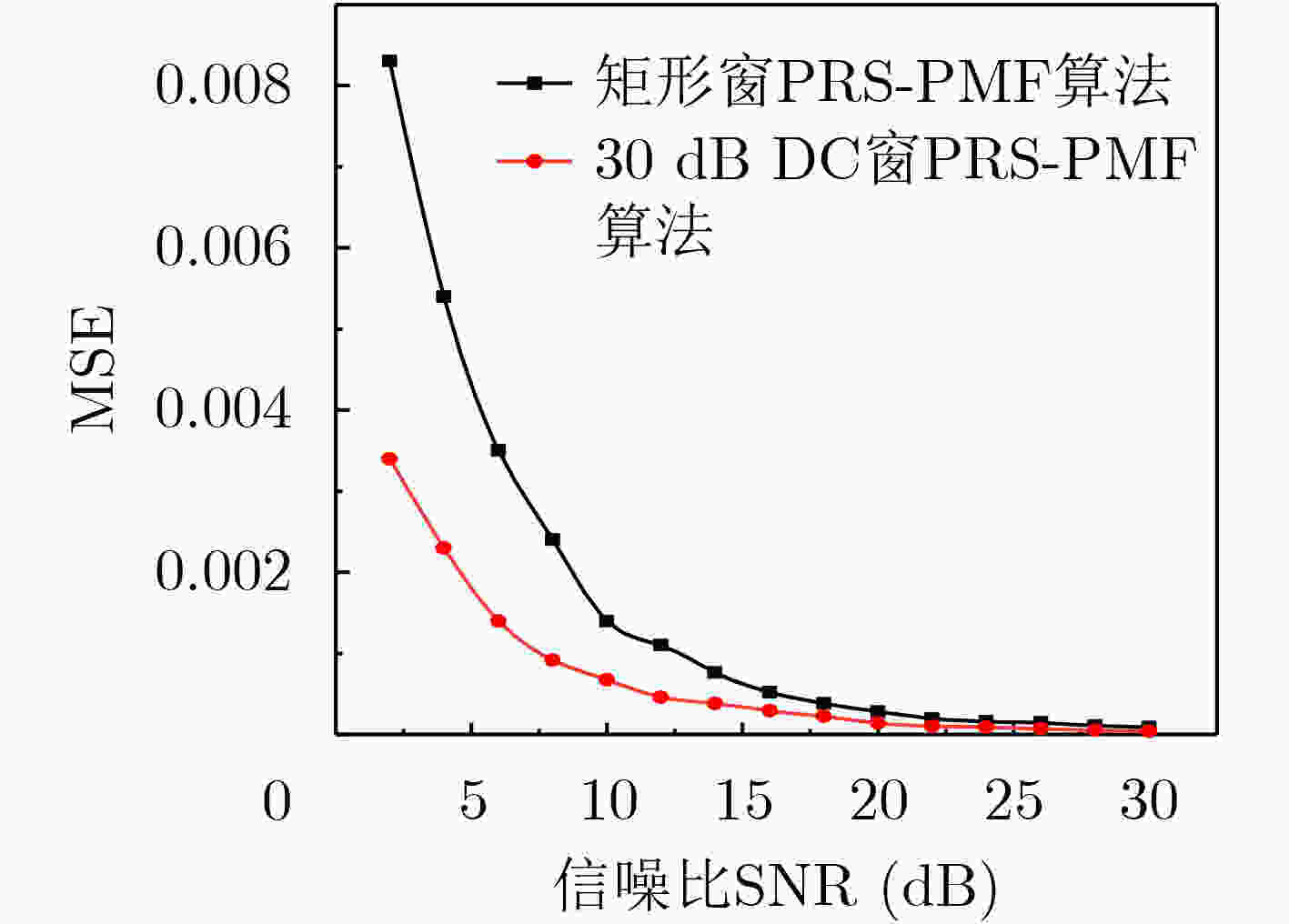
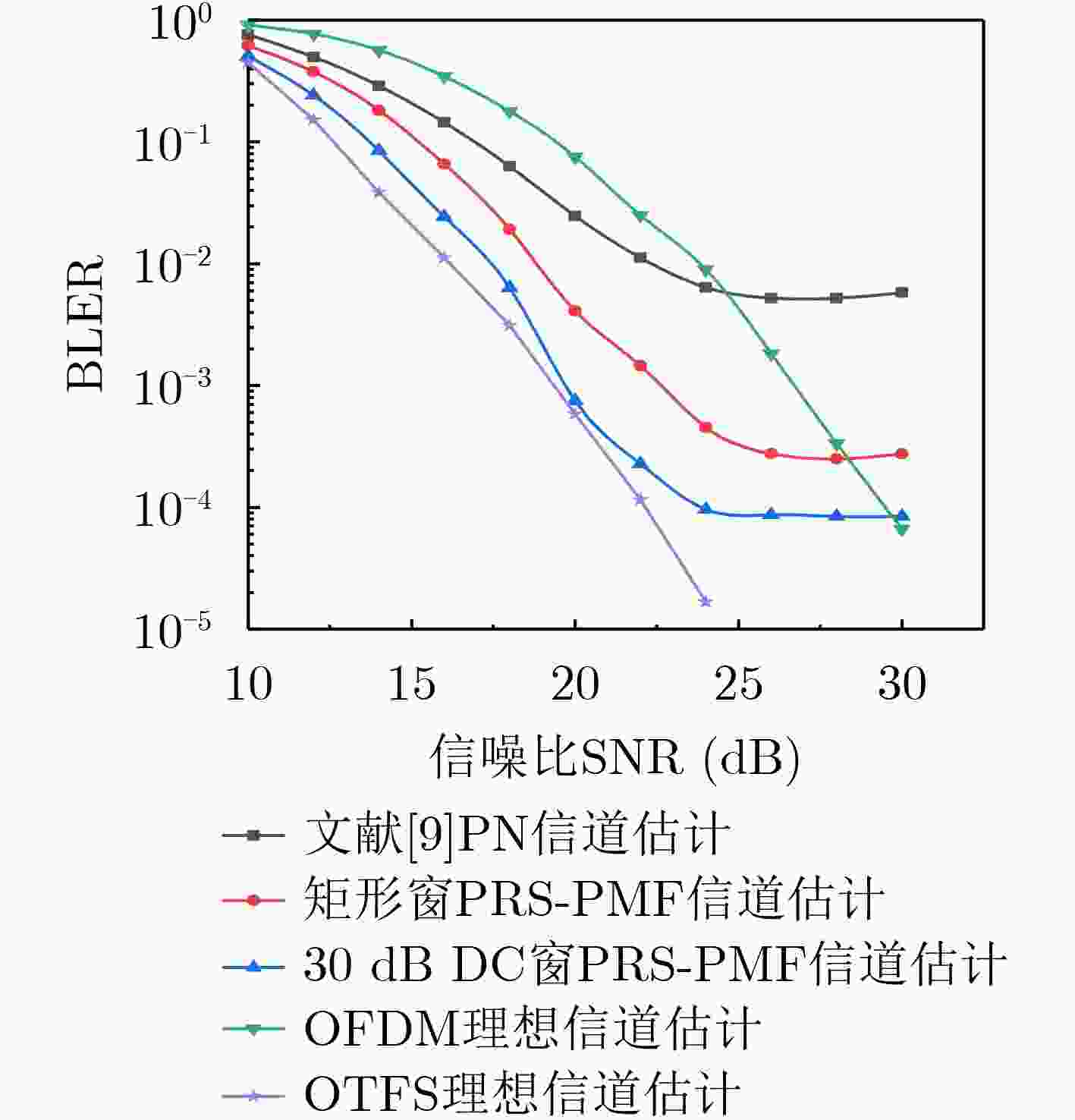
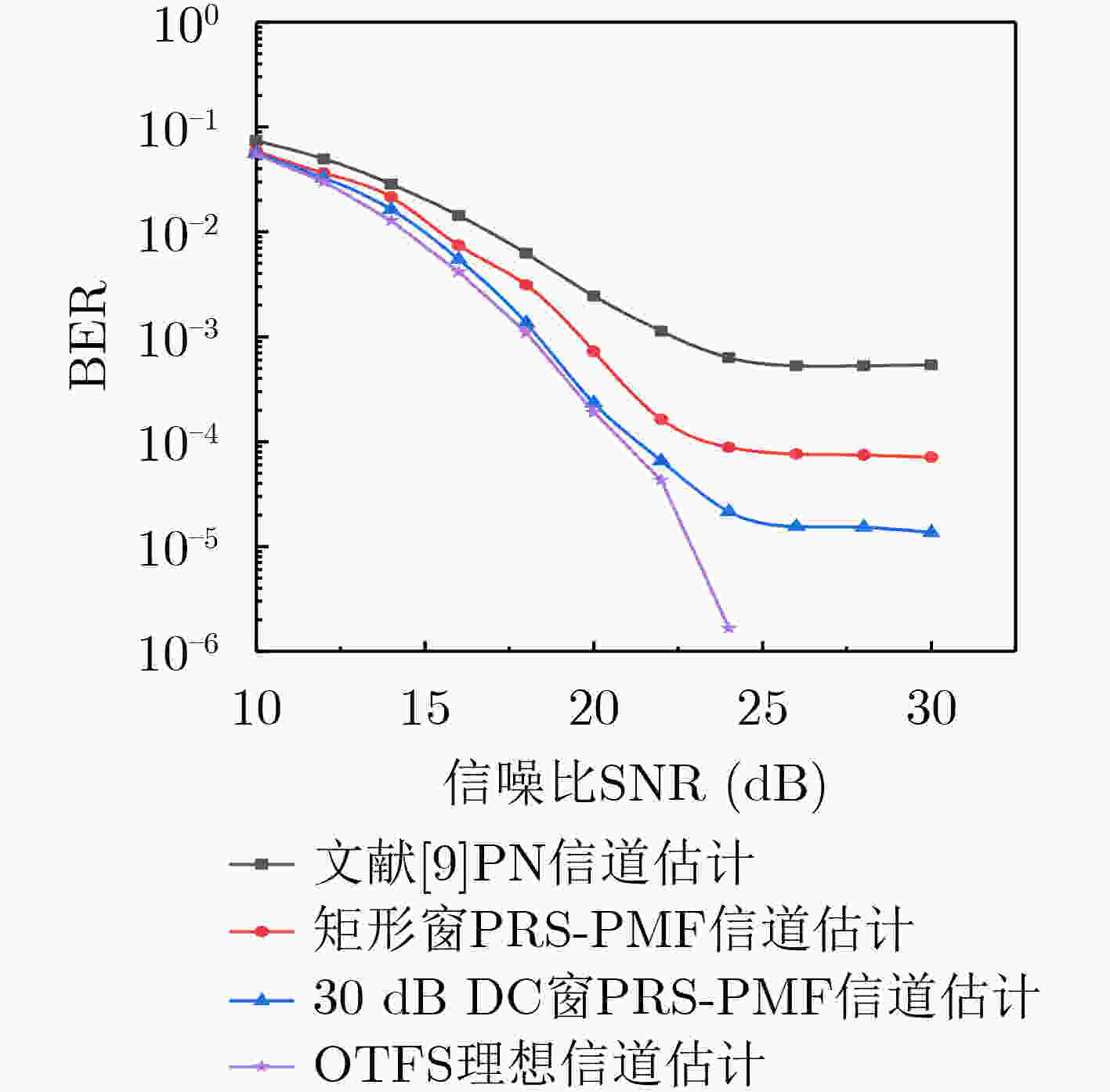
摘要: 针对正交时频空间(OTFS)调制系统中分数多普勒信道对应的物理路径信道状态信息估计困难及计算复杂度较高等问题，该文提出一种节省导频资源的脉冲匹配滤波(PRS-PMF)信道估计算法。该算法首先使用数据与导频联合成帧的嵌入式辅助导频方法获得等效信道的估计，然后通过互相关匹配滤波估计出各路径信道状态信息，相比于传统的脉冲导频互相关匹配滤波信道估计算法，能够在降低计算复杂度的同时减少导频资源的占用。在此基础上，对OTFS系统加窗，减少窗口响应主瓣的整数样点数量并降低旁瓣电平，有效改善了等效信道多普勒响应函数的自相关特性，从而降低了其他符号及噪声对估计符号的干扰。Abstract: In the Orthogonal Time-Frequency Space (OTFS) modulation system, it is difficult to estimate the Channel State Information (CSI) of physical path corresponding to fractional Doppler channel, and the computation is very complicated. To solve these problems, a channel estimation algorithm PRS-PMF (Pilot Resource Saving-Pulse Matched Filtering) for pulse matching filter which saves pilot resources is proposed. In the algorithm, the embedded auxiliary pilot is employed to obtain the equivalent channel estimation, then the CSI of each path is estimated through the cross-correlation matched filter. Compared with the traditional cross-correlation matched filter channel estimation algorithms, it can reduce the pilot resource occupy and the computational complexity. On this basis, the OTFS system is windowed to reduce the number of integer samples of the main lobe of the window response and reduce the side lobe level, which improves effectively the autocorrelation characteristics of the equivalent channel Doppler response function and thus reduces the interference of other symbols and noise on the estimated symbols.
-
图 5 不同旁瓣电平的DC窗口对加窗匹配函数
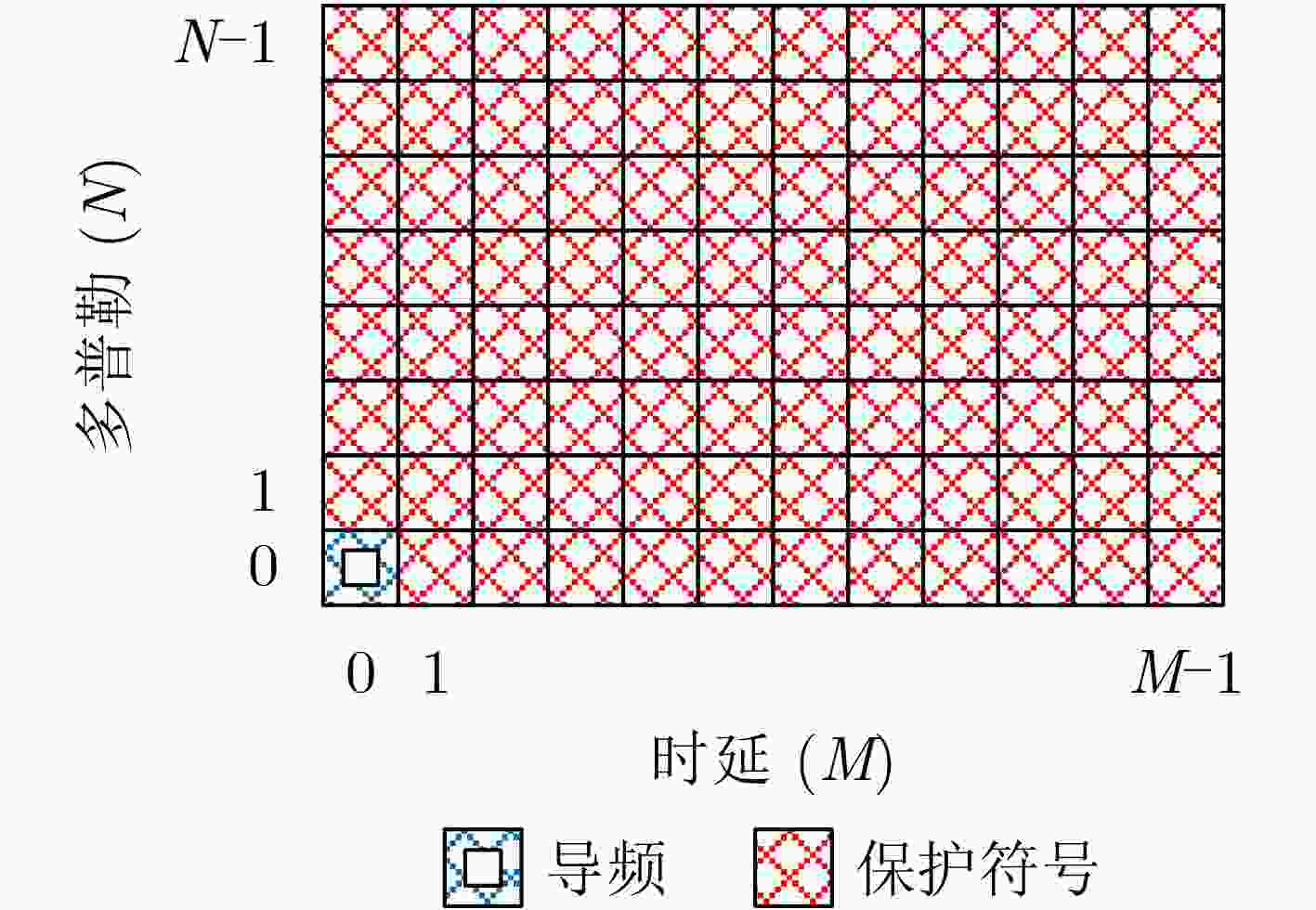
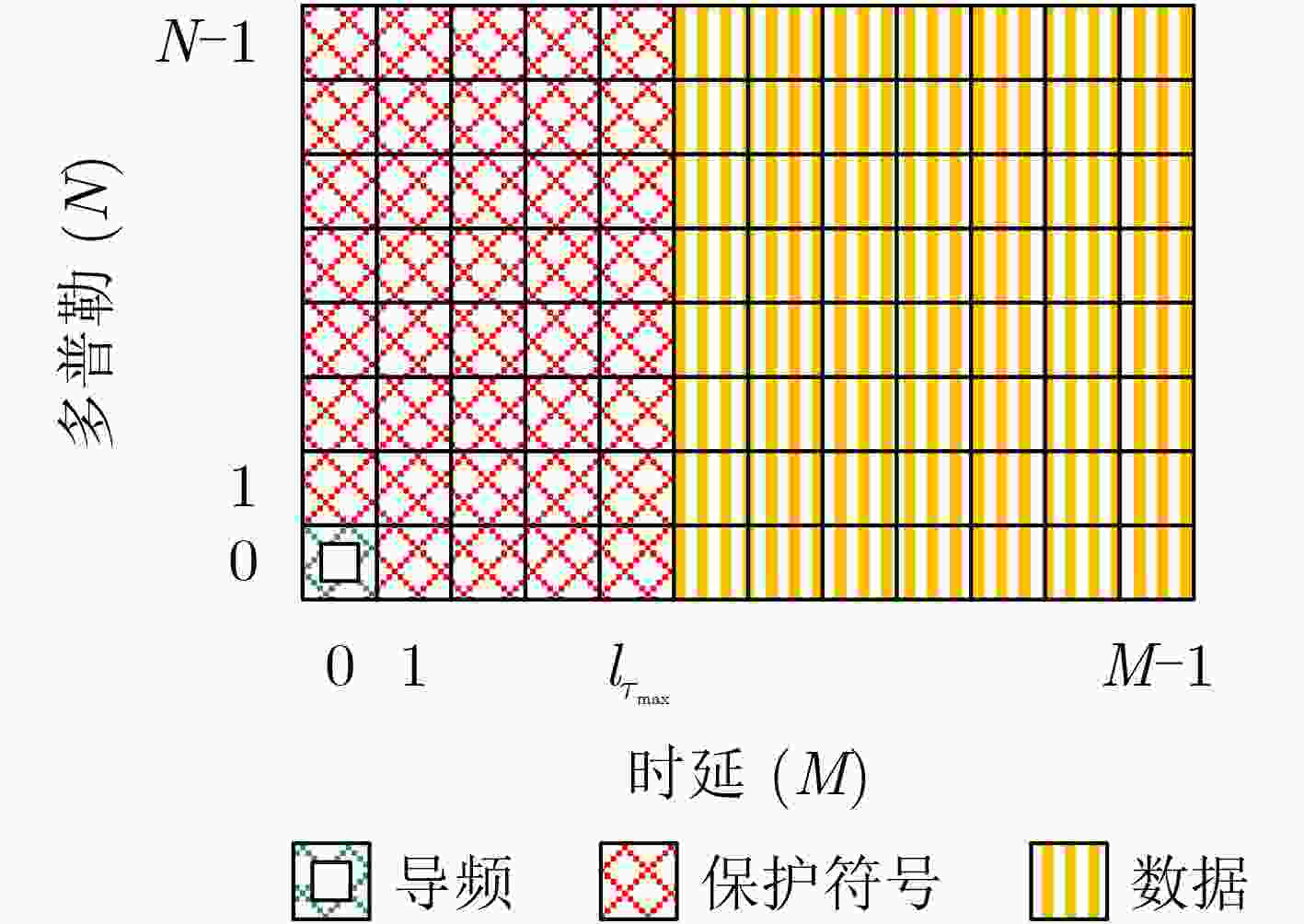
${\bar H_{{\text{EQ,}}\upsilon }}\left( {k - {k_{p,{\text{I}}}} - {k_{p,{\text{F}}}}} \right)$ 的影响表 1 导频图案资源占用率(%)比较
系统 嵌入式导频设计资源占用率$ {\eta _{{\text{PRS}}}} $ 文献[10]导频设计资源占用率$ \eta $ ${l_{{\tau _{\max }}}} = 3,M = 16$ 25.0 100 ${l_{{\tau _{\max }}}} = 6,M = 32$ 21.9 100 ${l_{{\tau _{\max }}}} = 16,M = 64$ 26.6 100 
下载: 导出CSV
表 3 本文PRS-PMF信道估计算法步骤
步骤 操作 描述 1 初始化 降低导频资源的信道响应$ {{\mathbf{\hat H}}_{{\text{EQ}}}} $，调节系数$\alpha $和$\beta $，噪声方差${\sigma ^2}$，$p \Leftarrow 1$ 2 遍历每个时延分量$\tilde l$并初始向量${\mathbf{h'}}$(1级循环) for每个时延分量$\tilde l$初始向量${\mathbf{h'}} \Leftarrow {{\mathbf{\hat H}}_{{\text{EQ}}}}\left[ {:,\tilde l} \right]$ 3 对于第$p$路径生成
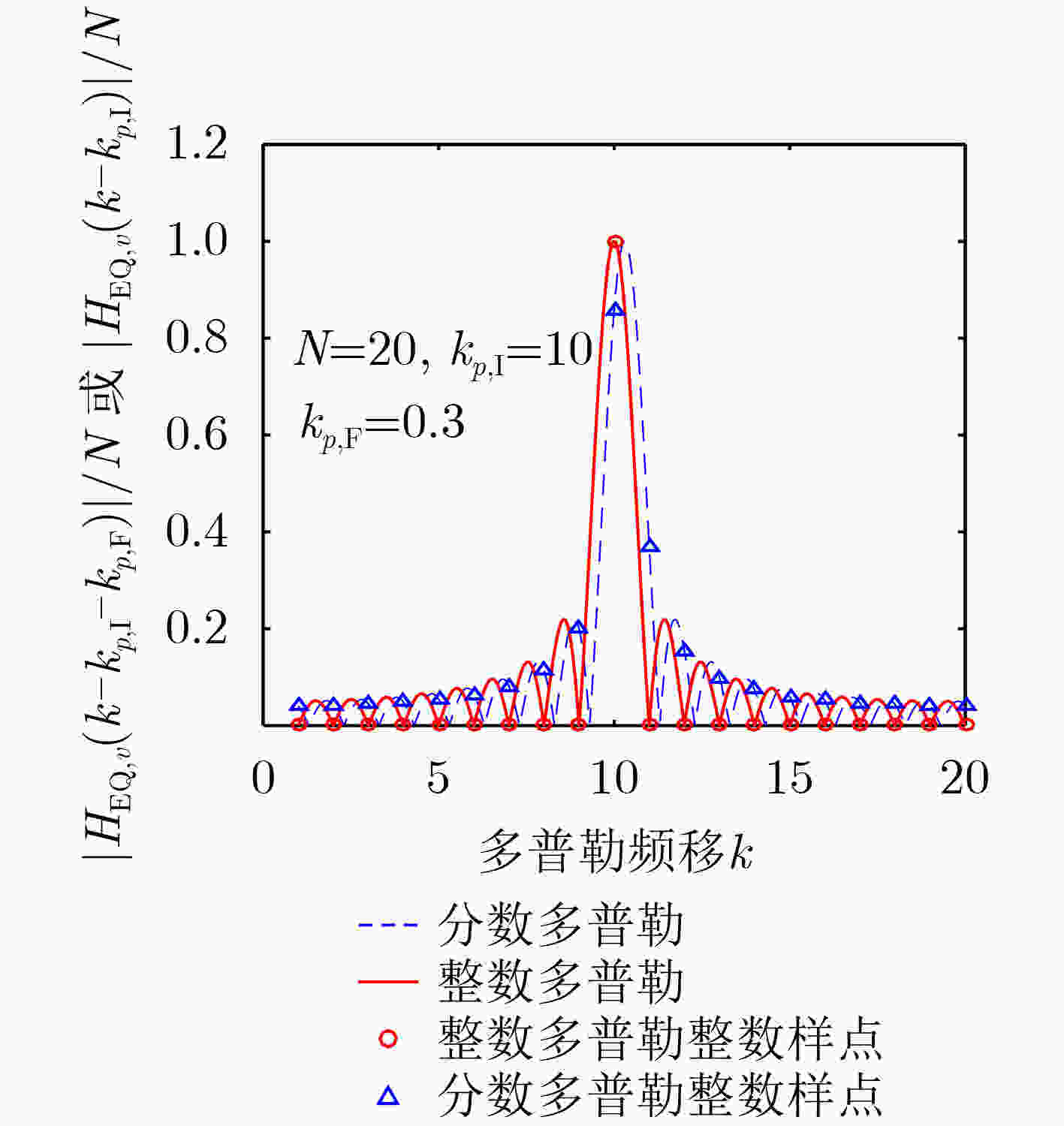
互相关矩阵(2级循环)for对于每个多普勒频移离散量整数部分$ {\tilde k_{\text{I}}} $和小数部分$ {\tilde k_{\text{F}}} $计算$ {R_{{\mathbf{h'}},{H_{{\text{EQ,}}\upsilon }}\left( {{{\tilde k}_{\text{I}}} + {{\tilde k}_{\text{F}}}} \right)}} $，组成向量$ {{\mathbf{R}}_{{\mathbf{h'}},{{\mathbf{H}}_{{\text{EQ,}}\upsilon }}}} $ 4 估算第$p$路径信道参数 寻找$ \left| {{{\mathbf{R}}_{{\mathbf{h'}},{{\mathbf{H}}_{{\text{EQ,}}\upsilon }}}}} \right| $最大时的$ {\tilde k_{\text{I}}} + {\tilde k_{\text{F}}} $，如果$ \left| {{{\mathbf{R}}_{{\mathbf{h'}},{H_{{\text{EQ,}}\upsilon }}\left( {{{\tilde k}_{\text{I}}} + {{\tilde k}_{\text{F}}}} \right)}}} \right| > {\hat h_{p - 1}} $，跳出循环，
否则根据式(14)估计各个参数5 更新${\mathbf{h'}}$ $ {\mathbf{h'}} \Leftarrow {\mathbf{h'}} - {\hat h_p}{{\text{e}}^{{\text{j}}{{\hat \phi }_p}}}{\hat \varphi _p}\left[ {{{\hat l}_p}} \right]{H_{{\text{EQ,}}\upsilon }}\left( {{{\hat k}_{p,{\text{I}}}} + {{\hat k}_{p,{\text{F}}}}} \right) $ 6 更新估计路径$p$ $p \Leftarrow p{\text{ + }}1$ 7 2级循环即关于$p$迭代
停止条件当满足$ \left| {{{\mathbf{R}}_{{\mathbf{h'}},{H_{{\text{EQ,}}\upsilon }}\left( {{{\hat k}_{p,{\text{I}}}} + {{\hat k}_{p,{\text{F}}}}} \right)}}} \right| < \left\{ \begin{gathered} \alpha \left| {\sum\nolimits_{d = 1}^N {{{\hat H}_{{\text{EQ}}}}\left[ {d,{{\hat l}_p}} \right]} } \right| \hfill \\ \beta \sigma \hfill \\ \end{gathered} \right. $ ，停止迭代转到步骤2，
否则转到步骤3继续迭代8 输出所有路径信道估计量 输出所有估计路径$p$的$ {\hat k_{p,{\text{I}}}} + {\hat k_{p,{\text{F}}}} $，$ {\hat l_p} $，$ {\hat h_p} $，$ {\hat \varphi _p} $，${{\rm{e}}^{ {\text{j} }{ {\hat \phi }_p} } }$
下载: 导出CSV
表 2 计算复杂度比较
系统 PRS-PMF算法计算复杂度 文献[10]算法计算复杂度 $N = 8,M = 16,P = 4$ $O\left( {15360} \right)$ $O\left( {40960} \right)$ $N = 16,M = 32,P = 6$ $O\left( {122880} \right)$ $O\left( {491520} \right)$ $N = 16,M = 64,P = 10$ $O\left( {409600} \right)$ $O\left( {1638400} \right)$
下载: 导出CSV
表 4 仿真参数设置
参数名称 参数数值 一个OTFS符号子载波数量(M) 256 OTFS符号数量(N) 32 载波频率$\left( {{f_c}} \right)$ 0.8 GHz 子载波间隔$\left( {\Delta f} \right)$ 15 kHz CP循环前缀长度$\left( {{M_{{\text{cp}}}}} \right)$ 17(6.67%M) 调制方式 16-QAM 信道编码 Turbo(1/2码率) 信道模型 EVA 用户速度 500 km/h 迭代停止系数$\alpha $ 1/100 迭代停止系数$\beta $ 1/40 搜索分数多普勒分辨率倒数$\left( D \right)$ 10 循环次数$\left( C \right)$ 20000
下载: 导出CSV
-
[1] HADANI R, RAKIB S, TSATSANIS M, et al. Orthogonal time frequency space modulation[C]. 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, USA, 2017: 1–6. [2] 解志斌, 薛同思, 田雨波, 等. 一种稀疏增强的压缩感知MIMO-OFDM信道估计算法[J]. 电子与信息学报, 2013, 35(3): 665–670. doi: 10.3724/SP.J.1146.2012.00860XIE Zhibin, XUE Tongsi, TIAN Yubo, et al. A sparsity enhanced channel estimation algorithm based on compressed sensing in MIMO-OFDM systems[J]. Journal of Electronics &Information Technology, 2013, 35(3): 665–670. doi: 10.3724/SP.J.1146.2012.00860 [3] SURABHI G D, AUGUSTINE R M, and CHOCKALINGAM A. On the diversity of uncoded OTFS modulation in doubly-dispersive channels[J]. IEEE Transactions on Wireless Communications, 2019, 18(6): 3049–3063. doi: 10.1109/TWC.2019.2909205 [4] DAS S and SCHNITER P. Max-SINR ISI/ICI-shaping multicarrier communication over the doubly dispersive channel[J]. IEEE Transactions on Signal Processing, 2007, 55(12): 5782–5795. doi: 10.1109/TSP.2007.901660 [5] SHEN Wenqian, DAI Linglong, AN Jianping, et al. Channel estimation for orthogonal time frequency space (OTFS) massive MIMO[J]. IEEE Transactions on Signal Processing, 2019, 67(16): 4204–4217. doi: 10.1109/TSP.2019.2919411 [6] RAVITEJA P, PHAN K T, JIN Qianyu, et al. Low-complexity iterative detection for orthogonal time frequency space modulation[C]. 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 2018: 1–6. [7] FISH A, GUREVICH S, HADANI R, et al. Delay-Doppler channel estimation in almost linear complexity[J]. IEEE Transactions on Information Theory, 2013, 59(11): 7632–7644. doi: 10.1109/TIT.2013.2273931 [8] RAVITEJA P, PHAN K T, and HONG Yi. Embedded pilot-aided channel estimation for OTFS in delay-Doppler channels[J]. IEEE Transactions on Vehicular Technology, 2019, 68(5): 4906–4917. doi: 10.1109/TVT.2019.2906357 [9] MURALI K R and CHOCKALINGAM A. On OTFS modulation for high-Doppler fading channels[C]. 2018 Information Theory and Applications Workshop (ITA), San Diego, USA, 2018: 1–10. [10] HASHIMOTO N, OSAWA N, YAMAZAKI K, et al. Channel estimation and equalization for CP-OFDM-based OTFS in fractional Doppler channels[C]. 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, Canada, 2021: 1–7. [11] 卢明飞, 彭思愿, 陈霸东. 最大互相关熵多凸组合自适应滤波算法[J]. 电子与信息学报, 2021, 43(2): 263–269. doi: 10.11999/JEIT200288LU Mingfei, PENG Siyuan, and CHEN Badong. Convex combination of multiple adaptive filters under the maximum correntropy criterion[J]. Journal of Electronics &Information Technology, 2021, 43(2): 263–269. doi: 10.11999/JEIT200288 [12] WEI Zhiqiang, YANG Weijie, LI Shuangyang, et al. Transmitter and receiver window designs for orthogonal time-frequency space modulation[J]. IEEE Transactions on Communications, 2021, 69(4): 2207–2223. doi: 10.1109/TCOMM.2021.3051386 [13] WEI Zhiqiang, NG D W K, and YUAN Jinhong. NOMA for hybrid mmWave communication systems with beamwidth control[J]. IEEE Journal of Selected Topics in Signal Processing, 2019, 13(3): 567–583. doi: 10.1109/JSTSP.2019.2901593 [14] 惠永涛, 李兵兵, 同钊, 等. 时频双选信道OFDM系统的低复杂度MMSE-SD算法[J]. 电子与信息学报, 2013, 35(2): 261–266. doi: 10.3724/SP.J.1146.2012.00805HUI Yongtao, LI Bingbing, TONG Zhao, et al. Low-complexity MMSE-SD algorithm for OFDM systems over doubly-selective channels[J]. Journal of Electronics &Information Technology, 2013, 35(2): 261–266. doi: 10.3724/SP.J.1146.2012.00805 -
下载:
图(9) / 表(4)
计量
- 文章访问数: 1157
- HTML全文浏览量: 485
- PDF下载量: 173
- 被引次数: 0
