Research on Optimization of Service Function Chain Path Based on Graph Attention Network
-
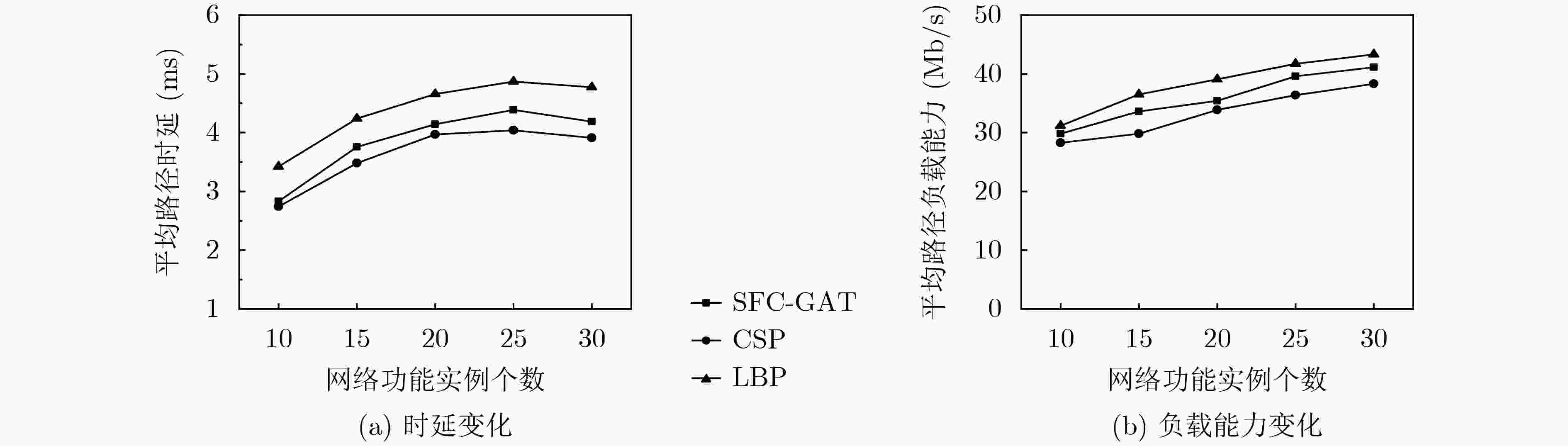
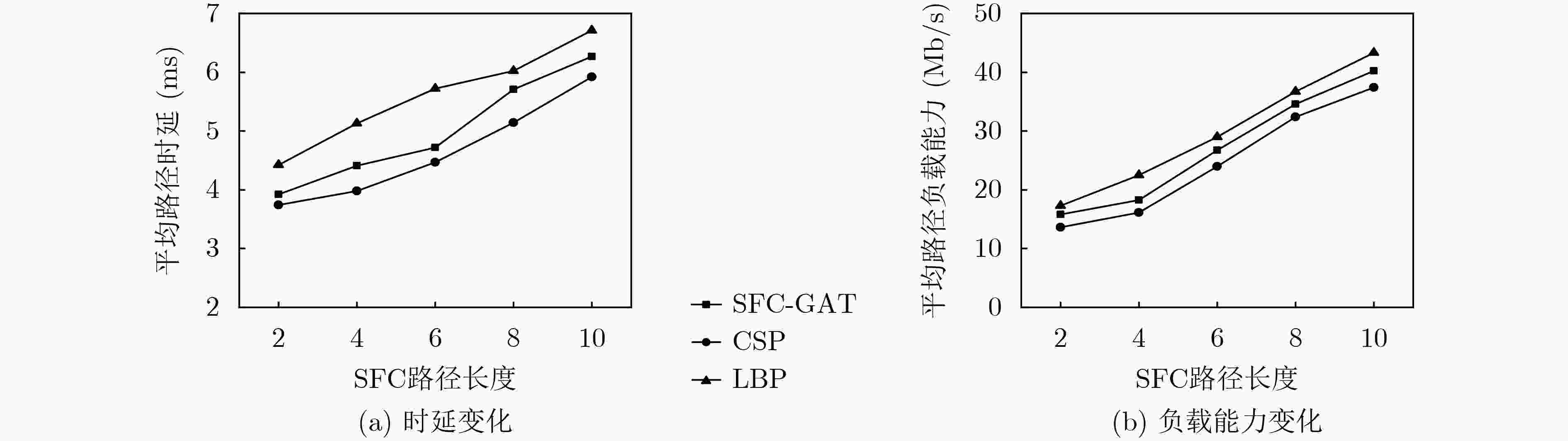
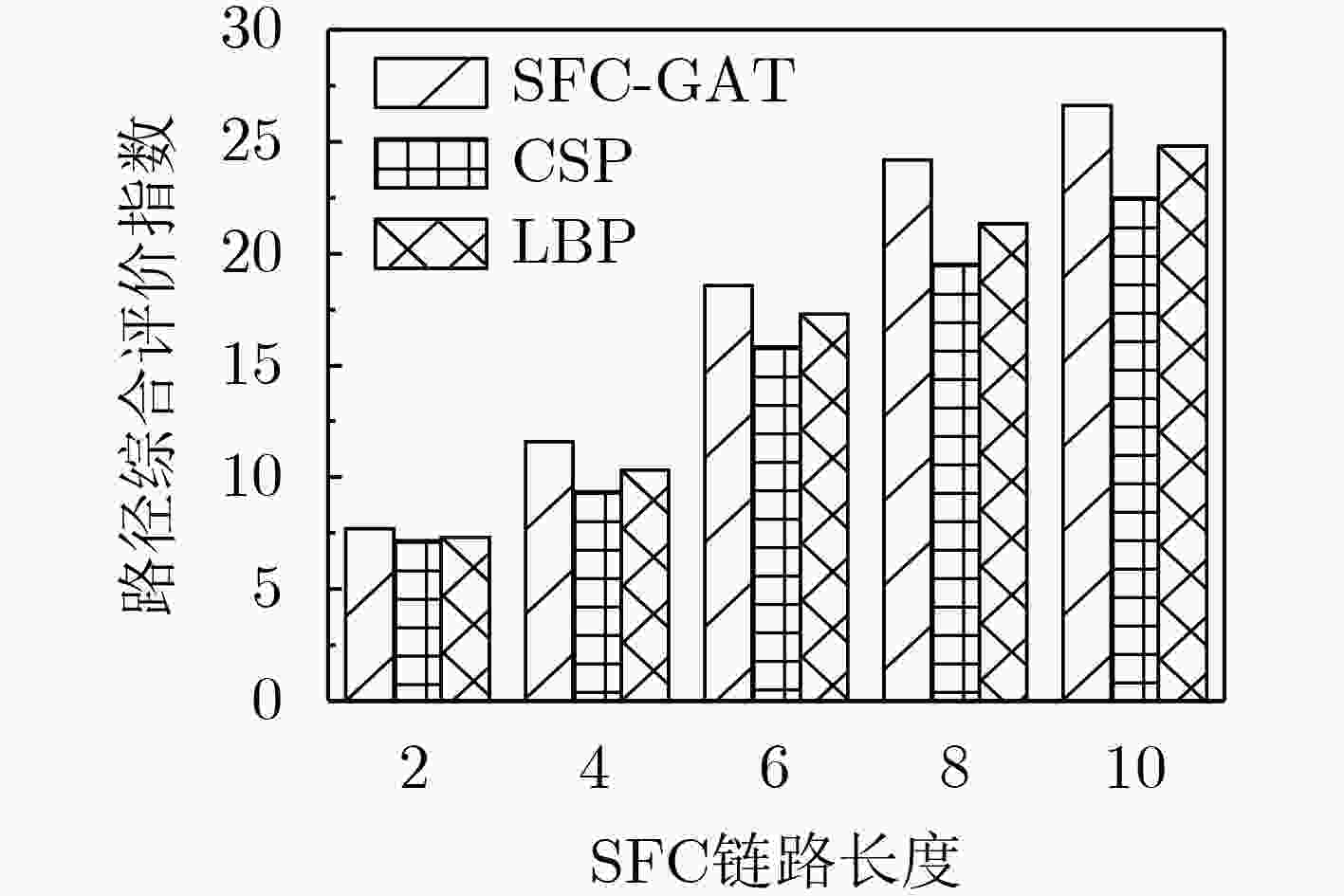
摘要: 服务功能链(SFC)路径生成旨在为用户提供高速率、低延迟的多样化网络功能定制服务。现有的SFC路径选择算法大多都针对特定网络拓扑结构或使用单一评价指标,存在泛化性弱、评价标准单一的问题。针对此,该文提出基于图注意力网络(GAT)的SFC路径选择优化模型(SFC-GAT),其核心不再固定网络拓扑结构,而是将SFC路径选择问题建模为路径注意力问题。通过重新设计路径选择图和路径更新策略方式,增强模型泛化性;从时延和负载能力综合角度评价路径优化效果,解决路径性能单一评价问题。仿真实验结果表明:相比于约束下最短路径和最小过载路径选择策略,SFC-GAT至少能提高12%和7%选择路径综合性能。Abstract: Service Function Chain (SFC) path generation aims to provide users with diversified network function customization services with high speed and low delay. Most of the existing SFC path selection algorithms aim at specific network topology or use a single evaluation index, which has the problems of weak generalization and single evaluation standard. In view of this, an SFC path selection optimization model (SFC-GAT) based on Graph ATtention network (GAT) is proposed. Its core is no longer to fix the network topology, but to model the SFC path selection problem as a path attention problem. The generalization of the model is enhanced by redesigning the path selection diagram and path update strategy; The effect of path optimization from the perspective of delay and load capacity is evaluated to solve the problem of single evaluation of path performance. The simulation results show that compared with the shortest path and minimum overload path selection strategy under constraints, SFC-GAT can improve the comprehensive performance of path selection by at least 12% and 7%.
-
表 1 GAT-SFC路径优化算法
输入 重构后SFC路径选择图$ G = \left( {u,V,E} \right) $ 输出 SFC预测路径 (1) Initialization (2) lr = 0.005 //学习率 (3) l2_coef = 0.0005 //权重衰减率 (4) Function GAT-SFC($ G=\left(u,V,E\right) $) (5) Initialization $ W $ //根据$ G $中节点的特征维度初始化 (6) For each $t\in \left\{1\cdots \mathrm{l}\mathrm{e}\mathrm{n}\left(u\right)-1\right\}$ //从第1层计算节点对
下层节点的注意力(7) For each $i\in \left\{1\cdots \mathrm{l}\mathrm{e}\mathrm{n}\left(t\right)\right\}$ //第t层一共多少个实例节点 (8) For each$j\in \left\{1\cdots \mathrm{l}\mathrm{e}\mathrm{n}(t+1)\right\}$//t+1层节点数量 (9) Update($ {\alpha }_{i,j}^{t,t+1} $) //根据式(7)计算两个节点之间的
注意力值(10) $ {p}_{\theta } $=$\mathrm{M}\mathrm{a}\mathrm{x}({\displaystyle\sum }_{i=1}^{n}{(\alpha }_{i,j}^{t,t+1})$ //根据式(8)整合预测结果,
得到预测路径(11) Loss = $ \mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(\mathrm{s}\mathrm{u}\mathrm{m}\right(L-{p}_{\theta })^2) $ //结果对比,计算损失值 (12) $ W $ = training(loss, lr, l2_coef) //更新权重 (13) End Function -
[1] PANDEY S, HONG J W K, and YOO J H. Q-Learning based SFC deployment on edge computing environment[C]. The 21st Asia-Pacific Network Operations and Management Symposium, Daegu, Korea (South), 2020: 220–226. [2] HUFF A, VENÂNCIO G, GARCIA V F, et al. Building multi-domain service function chains based on multiple NFV orchestrators[C]. 2020 IEEE Conference on Network Function Virtualization and Software Defined Networks, Leganes, Spain, 2020: 19–24. [3] 卢旭, 易波, 王兴伟, 等. SDN/NFV下的5G网络资源切片管理机制[J]. 小型微型计算机系统, 2021, 42(5): 1082–1087. doi: 10.3969/j.issn.1000-1220.2021.05.032LU Xu, YI Bo, WANG Xingwei, et al. 5G network resource slice management mechanism in software-defined networking/net-work function virtualization[J]. Journal of Chinese Computer Systems, 2021, 42(5): 1082–1087. doi: 10.3969/j.issn.1000-1220.2021.05.032 [4] Pham Chuan, Tran Nguyen H, Ren Shaolei, et al. Traffic-Aware and Energy-Efficient vNF Placement for Service Chaining: Joint Sampling and Matching Approach[J]. IEEE Transactions on Services Computing, 2020, 13(1): 172–185. doi: 10.1109/tsc.2017.2671867 [5] WANG Xiaolei, XIE Lijun, QIN Zhiqiang, et al. Clustering of virtual network function instances oriented to compatibility in 5G network[J]. China Communications, 2017, 14(12): 111–119. doi: 10.1109/cc.2017.8246341 [6] LIU Jiaqiang, LI Yong, ZHANG Ying, et al. Improve service chaining performance with optimized middlebox placement[J]. IEEE Transactions on Services Computing, 2017, 10(4): 560–573. doi: 10.1109/TSC.2015.2502252 [7] BREMLER-BARR A, HARCHOL Y, and HAY D. OpenBox: A software-defined framework for developing, deploying, and managing network functions[C]. 2016 ACM SIGCOMM Conference, Florianópolis, Brazil, 2016: 511–524. [8] GU Lin, ZENG Deze, LI Wei, et al. Intelligent VNF orchestration and flow scheduling via model-assisted deep reinforcement learning[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(2): 279–291. doi: 10.1109/JSAC.2019.2959182 [9] SUBRAMANYA T, HARUTYUNYAN D, and RIGGIO R. Machine learning-driven service function chain placement and scaling in MEC-enabled 5G networks[J]. Computer Networks, 2020, 166: 106980. doi: 10.1016/j.comnet.2019.106980 [10] CHOWDHURY P N, SHIVAKUMARA P, KANCHAN S, et al. Graph attention network for detecting license plates in crowded street scenes[J]. Pattern Recognition Letters, 2020, 140: 18–25. doi: 10.1016/j.patrec.2020.09.018 [11] 唐伦, 曹睿, 廖皓, 等. 基于深度强化学习的服务功能链可靠部署算法[J]. 电子与信息学报, 2020, 42(12): 2931–2938. doi: 10.11999/JEIT190969 [12] GU Yunjie, DING Yuehang, HU Yuxiang. Joint optimization of delay guarantees and resource allocation for service function Chaining[J]. IEICE Transactions on Information and Systems, 2019, E102.D(12): 2611–2614. [13] CLAYMAN S, MAINI E, GALIS A, et al. The dynamic placement of virtual network functions[C]. 2014 IEEE Network Operations and Management Symposium, Krakow, Poland, 2014: 1–9. [14] VELIČKOVIĆ P, CUCURULL G, CASANOVA A, et al. Graph attention networks[C]. The 6th International Conference on Learning Representations, Vancouver, Canada. 2018. [15] XIE Lijun, JIANG Yiming, WANG Binqiang, et al. An approach for network Function combination based on least busy placement algorithm[J]. China Communications, 2016, 13(S1): 167–176. -





 下载:
下载:



 下载:
下载:
