Motion Parameter Estimation Combined Smoothing Filter Algorithm Based on Gaussian Mixture Probability Hypothesis Density
-
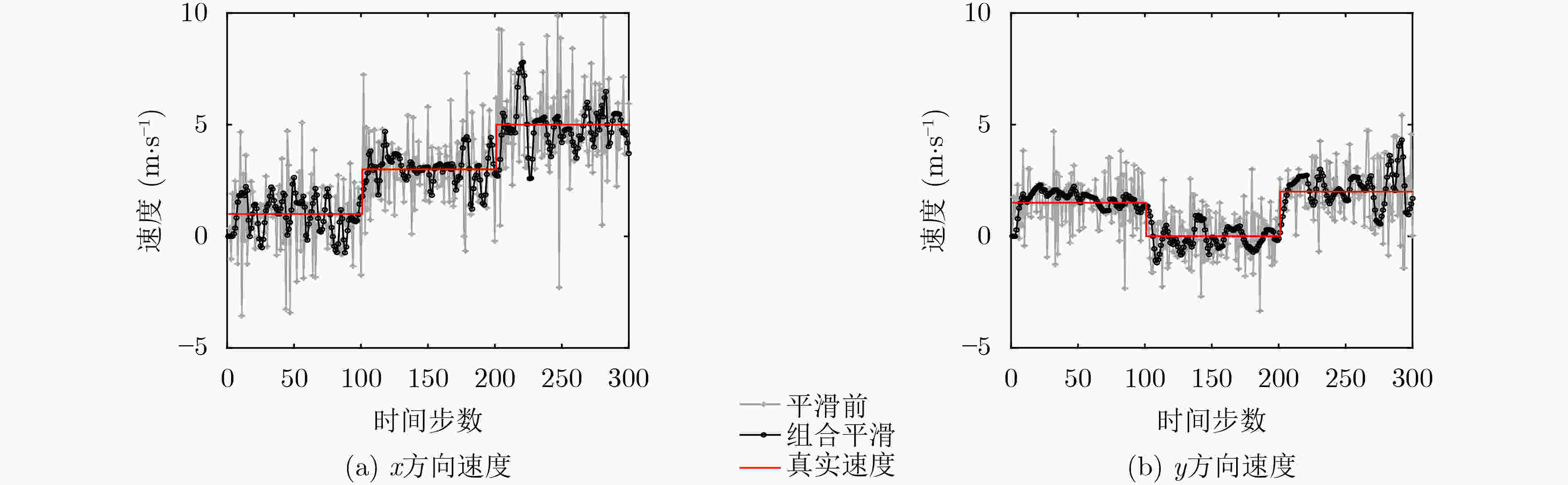
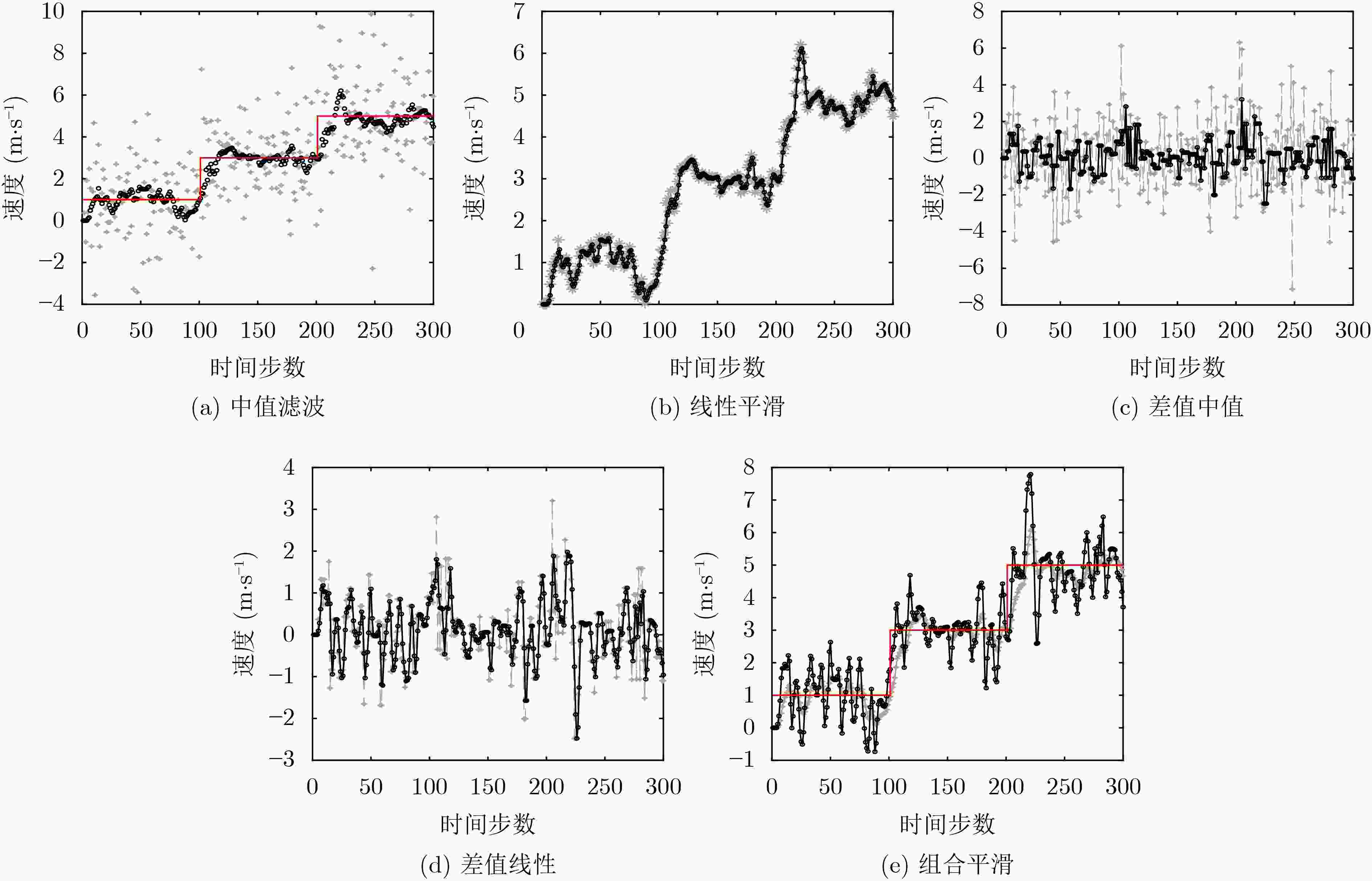
摘要: 针对高斯混合概率假设密度(GM-PHD)滤波器在目标速度未知或不准确时,目标状态估计性能较差,该文提出一种基于GM-PHD的运动参数估计组合平滑滤波算法。该算法通过目标状态提取速度信息,经过中值平滑和线性平滑组合处理提升速度估计准确性,然后将速度反馈给GM-PHD滤波器的状态转移方程,提高状态预测精度。仿真结果表明,目标速度未知或不准确时,所提算法能够明显改善GM-PHD滤波器状态估计性能。
-
关键词:
- 目标跟踪 /
- 高斯混合概率假设密度滤波 /
- 参数估计 /
- 组合平滑
Abstract: Considering poor performance of target state estimation for Gaussian Mixture Probability Hypothesis Density(GM-PHD) filter when the target velocity is unknown or inaccurate, a combined smoothing filtering algorithm for motion parameter estimation based on GM-PHD is proposed. The velocity information is extracted from the target state, and the accuracy of velocity estimation is improved through the combined processing of median smoothing and linear smoothing. Then, the velocity is fed back to the state transition equation of the GM-PHD filter to improve the accuracy of state prediction. Simulation results show that the proposed algorithm can significantly improve the state estimation performance of GM-PHD filter when the target velocity is unknown or inaccurate. -
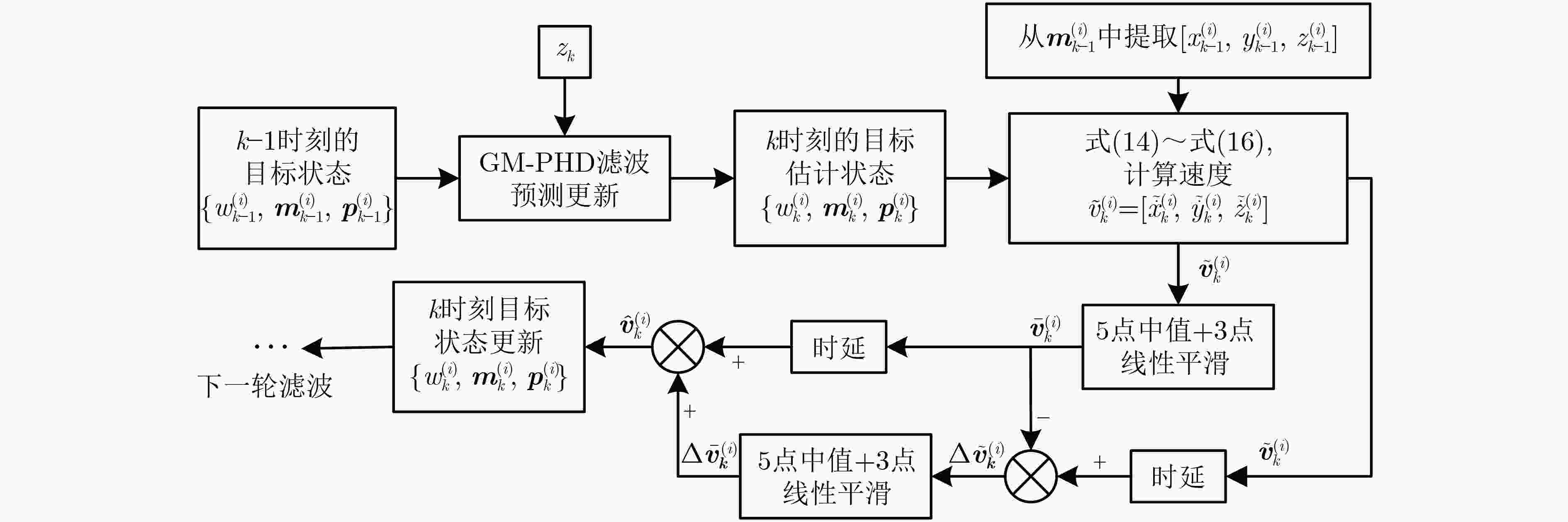
表 1 基于GM-PHD滤波器运动参数估计组合平滑算法
初始化$\tilde {\boldsymbol{v}} = \left[ {0,0,0,0} \right]$,$\Delta \tilde {\boldsymbol{v}} = \left[ {0,0,0,0} \right]$; 步骤1 由$\left\{ {w_{k - 1}^{\left( i \right)},{\boldsymbol{m}}_{k - 1}^{\left( i \right)},{\boldsymbol{p}}_{k - 1}^{\left( i \right)}} \right\}$进行GM-PHD滤波得到
$\left\{ {w_k^{\left( i \right)},{\boldsymbol{m}}_k^{\left( i \right)},{\boldsymbol{p}}_k^{\left( i \right)}} \right\}$;步骤2 从${\boldsymbol{m}}_{k - 1}^{\left( i \right)}$及${\boldsymbol{m}}_k^{\left( i \right)}$中获取$\left[ {x_{k - 1}^{\left( i \right)},y_{k - 1}^{\left( i \right)},z_{k - 1}^{\left( i \right)}} \right]$及
$\left[ {x_k^{\left( i \right)},y_k^{\left( i \right)},z_k^{\left( i \right)}} \right]$;步骤3 速度初步获取:根据式(14)~式(16)得到$\tilde{\dot{x}}_{k}^{\left( i \right)},\tilde{\dot{y}}_{k}^{\left( i \right)},\tilde{\dot{z}}_{k}^{\left( i \right)}$
后,送入组合平滑滤波器;步骤4 组合平滑处理:获得中值输出${{\boldsymbol{l}}_v}\left( k \right)$,再根据式(17)获得
$\bar {\boldsymbol{v}}_k^{\left( i \right)}$;步骤5 误差反馈:根据式(18)计算差值$\Delta \tilde {\boldsymbol{v}}_k^{\left( i \right)}$,经过中值滤波输
出${{\boldsymbol{l}}_{\Delta v}}\left( k \right)$,进行线性平滑输出$\Delta \bar {\boldsymbol{v}}_k^{\left( i \right)}$;步骤6 根据式(19)计算平滑滤波器的输出$\hat {\boldsymbol{v}}_k^{\left( i \right)}$; 步骤7 根据式(20)和式(21)更新$\tilde {\boldsymbol{m}}_k^{\left( i \right)}$和$\left\{ {w_k^{\left( i \right)},\tilde {\boldsymbol{m}}_k^{\left( i \right)},{\boldsymbol{p}}_k^{\left( i \right)}} \right\}$; 步骤8 下一时刻,重复步骤2~8。 表 2 实验参数设置
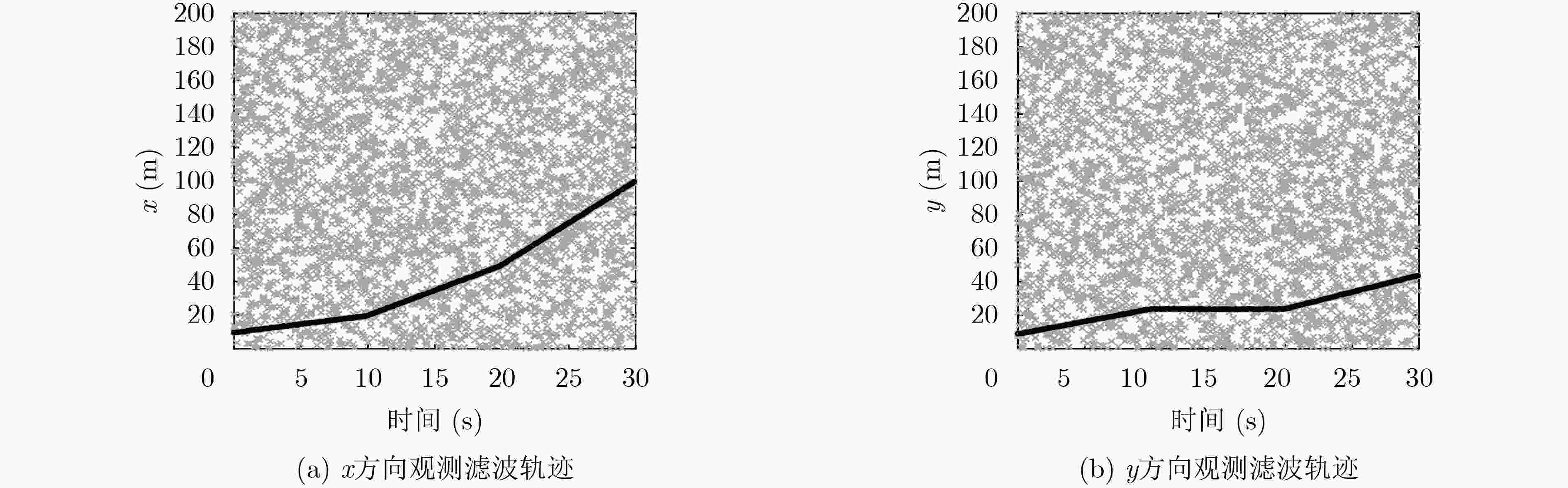
仿真参数 值 迭代时间间隔${{\mathit{\Delta}} _k}\left( s \right)$ 0.1 目标新生概率${p_{b,k}}$ 0.1 目标检测概率${p_{D,k}}$ 0.98 目标存活概率${p_{S,k}}$ 0.99 剪枝阈值$T$ 4 合并阈值$U$ 0.5 最大高斯分量数目${J_{\rm{max}}}$ 100 蒙特卡罗次数 100 杂波数$lc$ 20 过程噪声协方差${{\boldsymbol{Q}}_k}$ $1{0^{ - 2}}{{\boldsymbol{I}}_6}$ 表 3 不同过程噪声下算法的平均OSPA距离
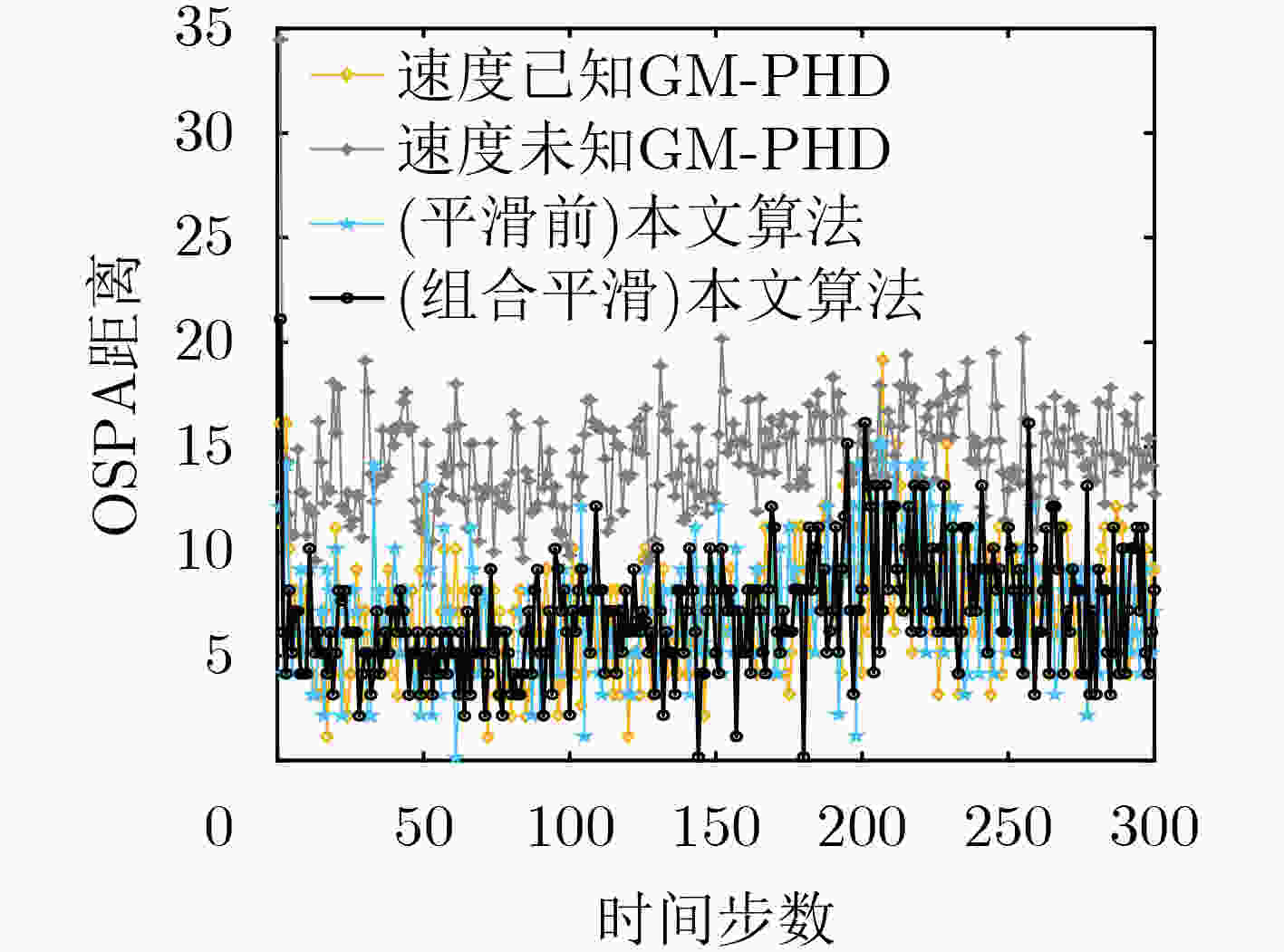
过程噪声(q) 0.005 0.01 0.050 0.100 0.500 速度未知GM-PHD 15.0502 14.4323 15.1557 15.1504 16.8850 (平滑前)本文算法 11.0243 7.0980 4.8090 5.0435 7.9587 (无差值补偿)本文算法 10.9665 7.1931 4.9964 5.0335 7.8285 (组合平滑)本文算法 10.7054 6.9934 4.7873 4.9872 7.5573 速度已知GM-PHD 10.9928 7.2449 5.0565 4.9300 7.9385 -
[1] MA Tianli, ZHANG Qi, CHEN Chaobo, et al. Tracking of maneuvering star-convex extended target using modified adaptive extended Kalman Filter[J]. IEEE Access, 2020, 8: 214030–214038. doi: 10.1109/ACCESS.2020.3029804 [2] XU Weijun. Adaptive probability hypothesis density filter for multi-target tracking with unknown measurement noise statistics[J]. Measurement and Control, 2021, 54(3/4): 279–291. [3] TIMOSHENKO A V, BABKIN Y V, SILANTYEV A B, et al. Detection and estimation of parameters of a random process set in multi-Scanning radar observation based on the "track-before-detect" methods[C]. 2021 Systems of Signals Generating and Processing in the Field of on Board Communications, Moscow, Russia, 2021: 1–5. [4] 杨丹, 姬红兵, 张永权. 未知杂波条件下样本集校正的势估计概率假设密度滤波算法[J]. 电子与信息学报, 2018, 40(4): 912–919. doi: 10.11999/JEIT170666YANG Dan, JI Hongbing, and ZHANG Yongquan. A cardinalized probability hypothesis density filter with unknown clutter estimation using corrected sample set[J]. Journal of Electronics &Information Technology, 2018, 40(4): 912–919. doi: 10.11999/JEIT170666 [5] ZHAO Shunyi, HUANG Biao, and LIU Fei. Linear optimal unbiased filter for time-variant systems without apriori information on initial conditions[J]. IEEE Transactions on Automatic Control, 2017, 62(2): 882–887. doi: 10.1109/TAC.2016.2557999 [6] TIAN Mingming, LIAO Guisheng, ZHU Shengqi, et al. A novel method for high-speed maneuvering target detection and motion parameters estimation[J]. Multidimensional Systems and Signal Processing, 2020, 31(4): 1625–1647. doi: 10.1007/s11045-020-00724-1 [7] 梁勇, 张友安, 刘京茂. 一种针对速度变化规律未知的导弹时间和角度控制方法[J]. 导弹与航天运载技术, 2019(6): 79–82. doi: 10.7654/j.issn.1004-7182.20190615LIANG Yong, ZHANG Youan, and LIU Jingmao. Impact time and impact angle control for missile with unknown velocity variation[J]. Missiles and Space Vehicles, 2019(6): 79–82. doi: 10.7654/j.issn.1004-7182.20190615 [8] 方卫红, 刘丽川, 杨继平, 等. 非迭代的波速未知声发射定位算法[J]. 后勤工程学院学报, 2016, 32(6): 1–7.FANG Weihong, LIU Lichuan, YANG Jiping, et al. A non-iterative AE source localization algorithm with unknown velocity[J]. Journal of Logistical Engineering University, 2016, 32(6): 1–7. [9] 刘哲, 卫军胡, 赵军, 等. 利用角度测量估计机动目标运动参数的方法[J]. 西安交通大学学报, 2009, 43(6): 67–71. doi: 10.3321/j.issn:0253-987X.2009.06.015LIU Zhe, WEI Junhu, ZHAO Jun, et al. A new parameter estimation method for flying target using bearing measurement[J]. Journal of Xi’an Jiaotong University, 2009, 43(6): 67–71. doi: 10.3321/j.issn:0253-987X.2009.06.015 [10] ZHANG Shuang, WANG Jun, ZHANG Xianchun, et al. Parameter adaptive tracking method for hypersonic vehicle with variable slip frequency model[C]. 2020 IEEE International Conference on Networking, Sensing and Control(ICNSC), Nanjing, China, 2020: 1–6. [11] VO B N and MA W K. The gaussian mixture probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4091–4104. doi: 10.1109/TSP.2006.881190 [12] 刘江义, 王春平. 基于双马尔科夫链的势概率假设密度滤波[J]. 电子与信息学报, 2019, 41(2): 492–497. doi: 10.11999/JEIT180352LIU Jiangyi and WANG Chunping. Cardinalized probability hypothesis density filter based on pairwise Markov chains[J]. Journal of Electronics &Information Technology, 2019, 41(2): 492–497. doi: 10.11999/JEIT180352 [13] 朱友清, 周石琳, 高贵. 结合聚类的GM-PHD滤波器辐射源群目标跟踪[J]. 系统工程与电子技术, 2015, 37(9): 1967–1973. doi: 10.3969/j.issn.1001-506X.2015.09.03ZHU Youqing, ZHOU Shilin, and GAO Gui. Emitter group targets tracking using GM-PHD filter combined with clustering[J]. Systems Engineering and Electronics, 2015, 37(9): 1967–1973. doi: 10.3969/j.issn.1001-506X.2015.09.03 [14] 罗纳德·马勒, 范红旗, 卢大威, 蔡飞, 译. 多源多目标统计信息融合进展[M]. 北京: 国防工业出版社, 2017: 2–22, 70–92.MAHLER R P S, FAN Hongqi, LU Dawei, and CAI Fei, translation. Advances in Statistical Multisource-Multitarget Information Fusion[M]. Beijing: National Defense Industry Press, 2017: 2–22, 70–92. [15] ZHANG Huanqing and GAO Li. An improved merging method for Gaussian mixture probability hypothesis density filter[J]. Optik, 2020, 207: 164282. doi: 10.1016/j.ijleo.2020.164282 [16] 张雪英. 数字语音处理及MATLAB仿真[M]. 2版. 北京: 电子工业出版社, 2016: 54–56.ZHANG Xueying. Digital Speech Processing and MATLAB Simulation[M]. 2nd ed. Beijing: Publishing House of Electronics Industry, 2016: 54–56. [17] WANG Yanhui, ZHANG Hongbin, and LI Yang. Iterated posterior linearization filters and smoothers with cross-correlated noises[J]. ISA Transactions, 2020, 100: 264–274. doi: 10.1016/j.isatra.2020.01.008 [18] SURENDRAN M, NATARAJAN S, BORDAS S P A, et al. Linear smoothed extended finite element method[J]. International Journal for Numerical Methods in Engineering, 2017, 112(12): 1733–1749. doi: 10.1002/nme.5579 [19] XIA Haiying, XIAO Yufang, SONG Shuxiang, et al. Quantum circuit design of approximate median filtering with noise tolerance threshold[J]. Quantum Information Processing, 2020, 19(6): 183. doi: 10.1007/s11128-020-02678-6 [20] EVERS C and NAYLOR P A. Optimized self-localization for SLAM in dynamic scenes using probability hypothesis density filters[J]. IEEE Transactions on Signal Processing, 2018, 66(4): 863–878. doi: 10.1109/TSP.2017.2775590 -





 下载:
下载:


 下载:
下载:
