Signal Parameter Estimation Algorithm for Orthogonal Dipole Array Based on Finite Rate of Innovation
-
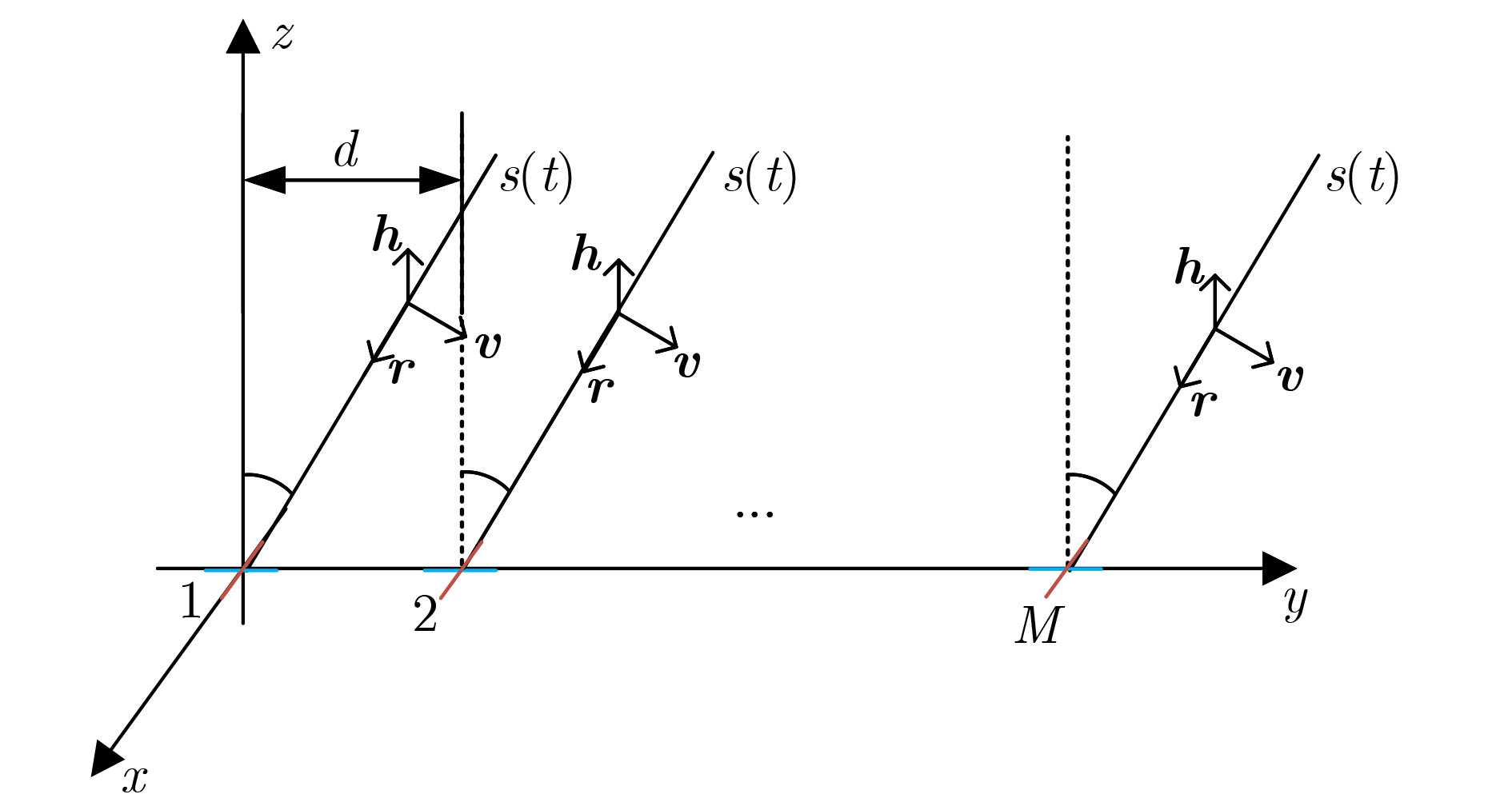
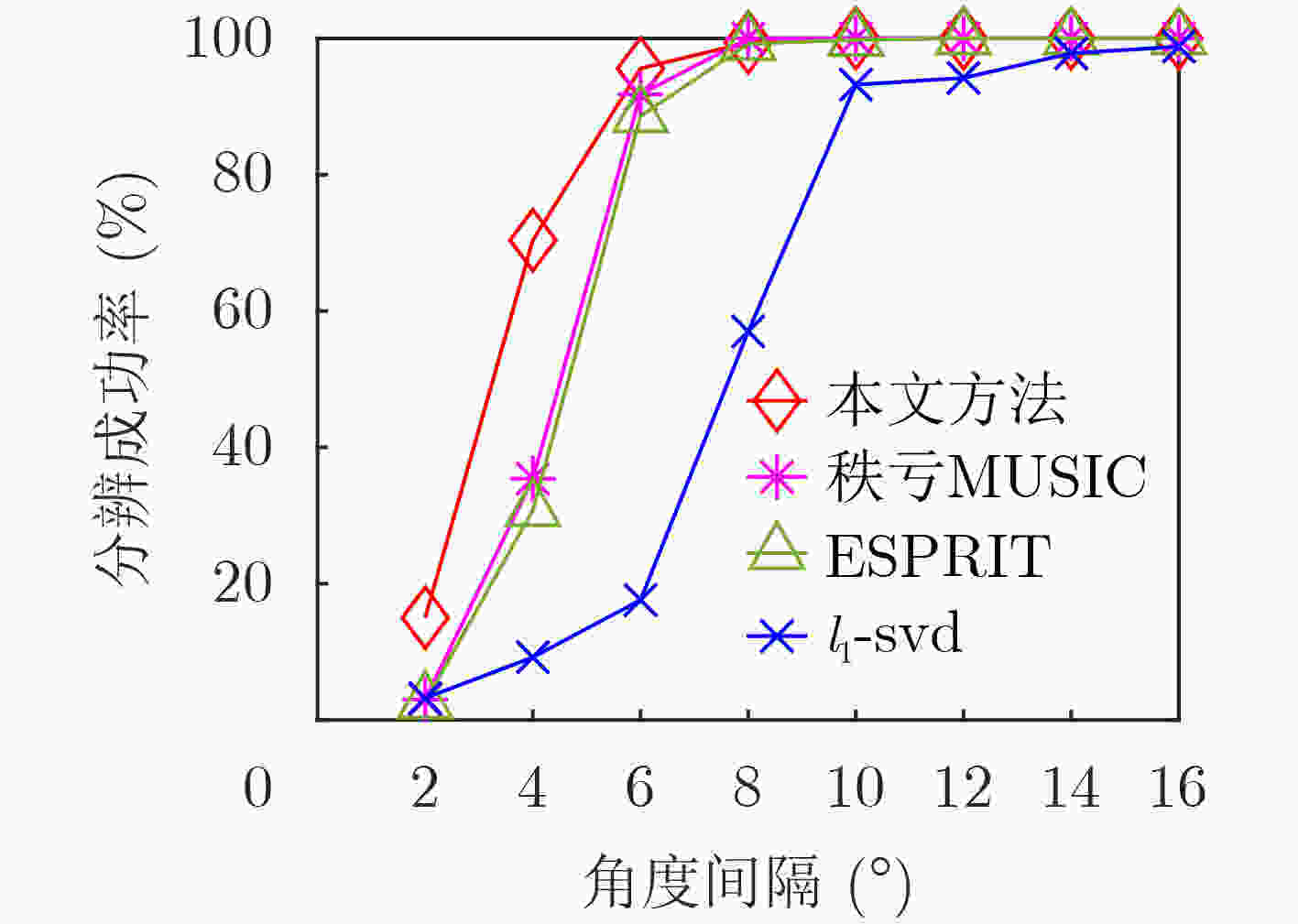
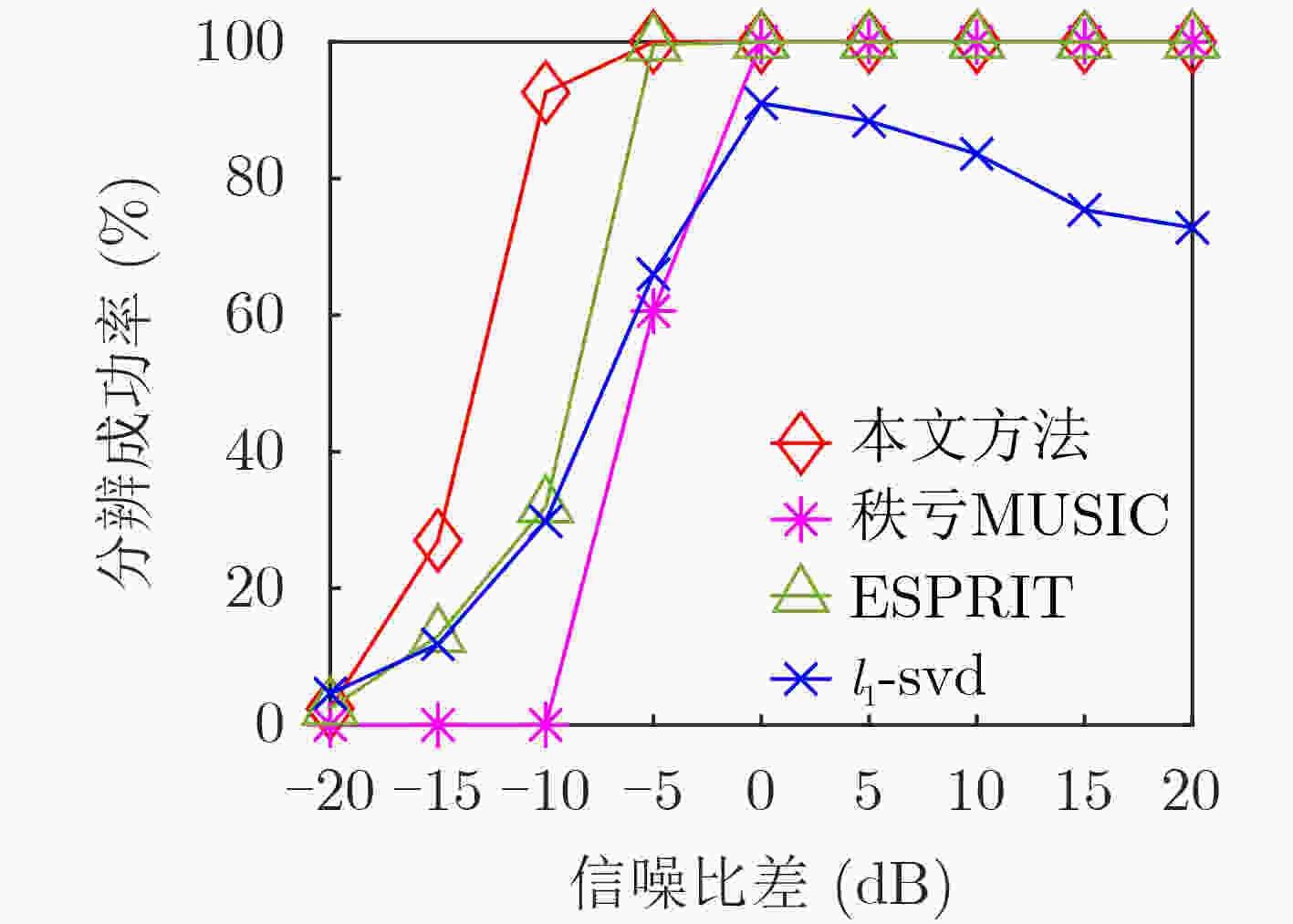
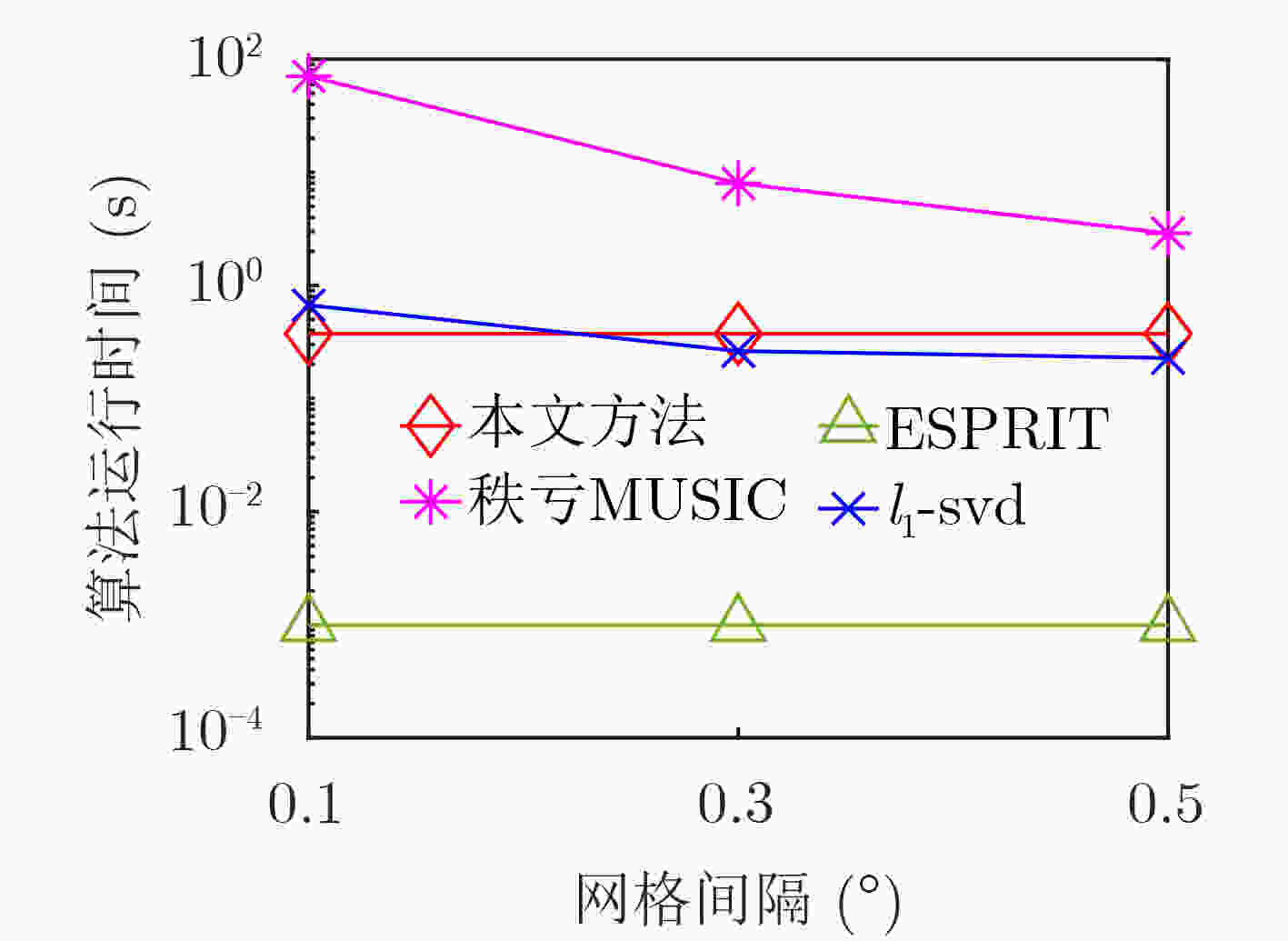
摘要: 为解决极化敏感阵列波达方向(DOA)估计中压缩感知类算法的网格失配问题,该文提出一种基于有限新息率(FRI)的正交偶极子阵列无网格信号参数估计算法。首先,利用均匀正交偶极子线阵中不同极化指向天线的两个子阵,求取其自相关矩阵之和,并通过协方差拟合准则恢复出满足Toeplitz结构的协方差矩阵。然后,利用该协方差矩阵构建FRI信号重构模型,求解以重构结果为系数的多项式的零点,就可以得到入射信号DOA参数的估计结果。最后,根据已估计出的DOA参数以及两个子阵的自相关矩阵和互相关矩阵,利用最小二乘法计算得到入射信号的极化参数估计结果。仿真实验表明,该算法与子空间类和压缩感知类算法相比,具有更高的估计精度及更好的角度分辨力。Abstract: To deal with the grid mismatch problem of compressed sensing algorithms in polarization-sensitive array Direction Of Arrival (DOA) estimation, a gridless signal parameter estimation algorithm for orthogonal dipole array based on Finite Rate of Innovation (FRI) is proposed. First, two sub-arrays of the uniform orthogonal dipole linear array with the different antenna polarization direction, are used to obtain the sum of their self-correlation covariance matrix, and the covariance matrix satisfying the Toeplitz structure is recovered through the covariance fitting criteria. Then, the covariance matrix is used to construct the FRI signal reconstruction model, and the zeros of the polynomial with the reconstruction result as the coefficient is solved to obtain the estimation result of the DOA parameter of the incident signal. Finally, using the estimated DOA parameters and the self-correlation covariance matrix and cross-correlation covariance matrix of the two sub-arrays, the least square method is used to calculate the polarization parameter estimation results of the incident signal. Simulation experiments show that this algorithm has higher estimation accuracy and angle resolution compared with subspace and compressed sensing algorithms.
-
表 1 算法流程
输入: 子阵1及子阵2接收的多快拍入射信号${{\boldsymbol{x}}_1}(t)$和${{\boldsymbol{x}}_2}(t)$; 初始化: 内部最大迭代次数${N_{{\rm{in}}} }$,外部最大迭代次数${N_{{\rm{out}}} }$,内部迭代次数$n = 1$,外部迭代次数$z = 1$,噪声容限$ \varepsilon $; 输出: 入射信源的DOA估计结果$ {\tilde \varphi _k} $及极化参数估计结果$ {\tilde \gamma _k} $和$ {\tilde \eta _k} $。 步骤1 计算${{\boldsymbol{x}}_1}(t)$和${{\boldsymbol{x}}_2}(t)$的自相关矩阵${{\boldsymbol{R}}_{11}}$, ${{\boldsymbol{R}}_{22}}$和互相关矩阵${{\boldsymbol{R}}_{12}}$,${{\boldsymbol{R}}_{21}}$,并计算${\boldsymbol{R}} = {{\boldsymbol{R}}_{11}} + {{\boldsymbol{R}}_{22}}$; 步骤2 求解式(13)中的半正定规划问题,得到优化变量$ {\boldsymbol{b}} $的结果$ {\boldsymbol{\tilde b}} $; 步骤3 根据式(16)和式(21)构造矩阵${\boldsymbol{\bar T}}({\boldsymbol{\tilde b}})$; 步骤4 随机初始化$ {{\boldsymbol{\bar c}}_0} \ne {\boldsymbol{0}} $; 步骤5 根据式(17)和式(21)构造矩阵$ {\boldsymbol{\bar R}}({{\boldsymbol{\bar c}}^{(n{{\rm{ - }}}1)}}) $; 步骤6 求解式(19)的非齐次线性方程组,得到$ {{\boldsymbol{\bar c}}^{(n)}} $并构造矩阵$ {\boldsymbol{\bar R}}({{\boldsymbol{\bar c}}^{(n)}}) $; 步骤7 求解式(20)的非齐次线性方程组,得到$ {{\boldsymbol{\bar b}}^{(n)}} $; 步骤8 判断$\left\| {{\boldsymbol{\bar {\tilde b}}} - {\boldsymbol{\bar b}}} \right\|_2^2 \le \varepsilon $是否成立,若成立,则进入步骤11,否则$n = n + 1$; 步骤9 判断$n \le {N_{{\rm{in}}} }$是否成立,若成立,则返回步骤5,否则$z = z + 1$; 步骤10 判断$z \le {N_{{\rm{out}}} }$是否成立,若成立,则返回步骤4,否则继续下一步骤; 步骤11 根据式将${{\boldsymbol{\bar c}}^{(n)}}$转换回复数形式${\boldsymbol{\tilde c}}$,并以${\boldsymbol{\tilde c}}$为系数,建立如式(14)的多项式,根据式(22)计算DOA参数$ {\tilde \varphi _k} $; 步骤12 将估计出的$ {\tilde \varphi _k} $代回$ {\boldsymbol{\tilde U}} = ({\boldsymbol{A}}_u^* \odot {{\boldsymbol{A}}_u}) $,并将${{\boldsymbol{R}}_{ij}}$向量化得到${{\boldsymbol{r}}_{ij}}$; 步骤13 根据式(23)计算$ {{\boldsymbol{\tilde p}}_{ij}} $; 步骤14 根据式(24)和式(25)计算得到极化参数估计结果$ {\tilde \gamma _k} $和$ {\tilde \eta _k} $。 -
[1] WAN Liangtian, LIU Kaihui, LIANG Yingchang, et al. DOA and polarization estimation for non-circular signals in 3-D millimeter wave polarized massive MIMO systems[J]. IEEE Transactions on Wireless Communications, 2021, 20(5): 3152–3167. doi: 10.1109/TWC.2020.3047866 [2] 王琦森, 余华, 李杰, 等. 基于稀疏贝叶斯学习的空间紧邻信号DOA估计算法[J]. 电子与信息学报, 2021, 43(3): 708–716. doi: 10.11999/JEIT200656WANG Qisen, YU Hua, LI Jie, et al. Sparse Bayesian learning based algorithm for DOA estimation of closely spaced signals[J]. Journal of Electronics &Information Technology, 2021, 43(3): 708–716. doi: 10.11999/JEIT200656 [3] 李槟槟, 张袁鹏, 陈辉, 等. 分离式长电偶极子稀疏阵列的相干信号多维参数联合估计[J]. 电子与信息学报, 2021, 43(9): 2695–2702. doi: 10.11999/JEIT200515LI Binbin, ZHANG Yuanpeng, CHEN Hui, et al. Coherent sources multidimensional parameters estimation with a sparse array of spatially spread long electric-dipoles[J]. Journal of Electronics &Information Technology, 2021, 43(9): 2695–2702. doi: 10.11999/JEIT200515 [4] SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830 [5] ROY R and KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 984–995. doi: 10.1109/29.32276 [6] FERRARA E and PARKS T. Direction finding with an array of antennas having diverse polarizations[J]. IEEE Transactions on Antennas and Propagation, 1983, 31(2): 231–236. doi: 10.1109/TAP.1983.1143038 [7] LI J. Direction and polarization estimation using arrays with small loops and short dipoles[J]. IEEE Transactions on Antennas and Propagation, 1993, 41(3): 379–387. doi: 10.1109/8.233120 [8] 徐友根, 刘志文. 残缺电磁矢量阵列直线信号波达方向估计[J]. 电子与信息学报, 2009, 31(4): 861–864. doi: 10.3724/SP.J.1146.2007.01471XU Yougen and LIU Zhiwen. DOA estimation of rectilinear signals using defective electromagnetic vector arrays[J]. Journal of Electronics &Information Technology, 2009, 31(4): 861–864. doi: 10.3724/SP.J.1146.2007.01471 [9] 徐丽琴, 李勇, 付银娟, 等. 基于降维实值ESPRIT的多输入多输出雷达波达方向估计[J]. 吉林大学学报:工学版, 2020, 50(3): 1113–1119. doi: 10.13229/j.cnki.jdxbgxb20190014XU Liqin, LI Yong, FU Yinjuan, et al. Reduced-dimensional real-valued ESPRIT algorithm for direction of arrival estimation in MIMO radar[J]. Journal of Jilin University:Engineering and Technology Edition, 2020, 50(3): 1113–1119. doi: 10.13229/j.cnki.jdxbgxb20190014 [10] 刘鲁涛, 王传宇. 基于极化敏感阵列均匀线阵的二维DOA估计[J]. 电子与信息学报, 2019, 41(10): 2350–2357. doi: 10.11999/JEIT180832LIU Lutao and WANG Chuanyu. Two dimensional DOA estimation based on polarization sensitive array and uniform linear array[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2350–2357. doi: 10.11999/JEIT180832 [11] BAIDOO E, HU Jurong, ZENG Bao, et al. Joint DOD and DOA estimation using tensor reconstruction based sparse representation approach for bistatic MIMO radar with unknown noise effect[J]. Signal Processing, 2021, 182: 107912. doi: 10.1016/j.sigpro.2020.107912 [12] CHALISE B K, ZHANG Y D, and HIMED B. Compressed sensing based joint DOA and polarization angle estimation for sparse arrays with dual-polarized antennas[C]. 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, USA, 2018: 251–255. [13] CHEN Tao, YANG Jian, WANG Weitong, et al. Generalized sparse polarization array for DOA estimation using compressive measurements[J]. Wireless Communications and Mobile Computing, 2021, 2021: 5539709. doi: 10.1155/2021/5539709 [14] VETTERLI M, MARZILIANO P, and BLU T. Sampling signals with finite rate of innovation[J]. IEEE Transactions on Signal Processing, 2002, 50(6): 1417–1428. doi: 10.1109/tsp.2002.1003065 [15] BLU T, DRAGOTTI P L, VETTERLI M, et al. Sparse sampling of signal innovations[J]. IEEE Signal Processing Magazine, 2008, 25(2): 31–40. doi: 10.1109/MSP.2007.914998 [16] PAN Haijie, BLU T, and VETTERLI M. Towards generalized FRI sampling with an application to source resolution in radioastronomy[J]. IEEE Transactions on Signal Processing, 2017, 65(4): 821–835. doi: 10.1109/TSP.2016.2625274 [17] PAN Hanjie, SCHEIBLER R, BEZZAM E, et al. FRIDA: FRI-based DOA estimation for arbitrary array layouts[C]. 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, USA, 2017: 3186–3190. [18] PAN Yujian, LUO Guoqing, JIN Huayan, et al. DOA estimation with planar array via spatial finite rate of innovation reconstruction[J]. Signal Processing, 2018, 153: 47–57. doi: 10.1016/j.sigpro.2018.07.001 [19] CHEN Tao, SHI Lin, and YU Yongzhi. Gridless DOA estimation with finite rate of innovation reconstruction based on symmetric Toeplitz covariance matrix[J]. EURASIP Journal on Advances in Signal Processing, 2020, 2020(1): 44. doi: 10.1186/s13634-020-00701-7 [20] YANG Zai, XIE Lihua, and ZHANG Cishen. A discretization-free sparse and parametric approach for linear array signal processing[J]. IEEE Transactions on Signal Processing, 2014, 62(19): 4959–4973. doi: 10.1109/TSP.2014.2339792 [21] BRESLER Y and MACOVSKI A. Exact maximum likelihood parameter estimation of superimposed exponential signals in noise[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1986, 34(5): 1081–1089. doi: 10.1109/TASSP.1986.1164949 [22] GILLIAM C and BLU T. Finding the minimum rate of innovation in the presence of noise[C]. 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 2016: 4019–4023. -





 下载:
下载:


 下载:
下载:
