带精英集并行遗传算法的无人机干扰资源调度

邓敏; 伍志高; 姚志强; 陈永其

doi:10.11999/JEIT210349

带精英集并行遗传算法的无人机干扰资源调度

doi: 10.11999/JEIT210349

邓敏^{1, 2, ,},
伍志高²,
姚志强²,
陈永其¹

1.
中国电子科技集团第36研究所通信信息控制和安全技术重点实验室嘉兴 314000
2.
湘潭大学自动化与电子信息学院湘潭 411105

基金项目: 湖南省自然科学基金(2019JJ50620)，国家重点研发计划(2020YFA0713502)，GF科技重点实验室基金(61421060404)

详细信息

作者简介:
邓敏：女，1987年生，讲师，研究方向为通信干扰对抗、认知无线电

伍志高：男，1997年生，硕士生，研究方向为干扰资源调度

姚志强：男，1975年生，教授，研究方向为导航定位、下一代宽带无线通信

陈永其：男，1969年生，研究员级高级工程师，研究方向为数字信号处理、特种通信

通讯作者:
邓敏　iemdeng@xtu.edu.cn

中图分类号: TN974; TN972
计量
- 文章访问数: 707
- HTML全文浏览量: 290
- PDF下载量: 72
- 被引次数: 6
出版历程
- 收稿日期: 2021-04-23
- 修回日期: 2021-10-12
- 网络出版日期: 2022-04-17
- 刊出日期: 2022-06-21

Unmanned Aerial Vehicle Jamming Resource Scheduling Based on Parallel Genetic Algorithm with Elite Set

1.
Science and Technology on Communication Information Security Control Laboratory, No. 36 Research Institute of China Electronics Technology Group Corporation, Jiaxing 314000, China
2.
School of Automation and Electronic Information, Xiangtan University, Xiangtan 411105, China

Funds: The Provincial Natural Science Foundation of Hunan (2019JJ50620), The National Key R&D Program of China (2020YFA0713502), The National Science Key Laboratory Foundation (61421060404)

摘要

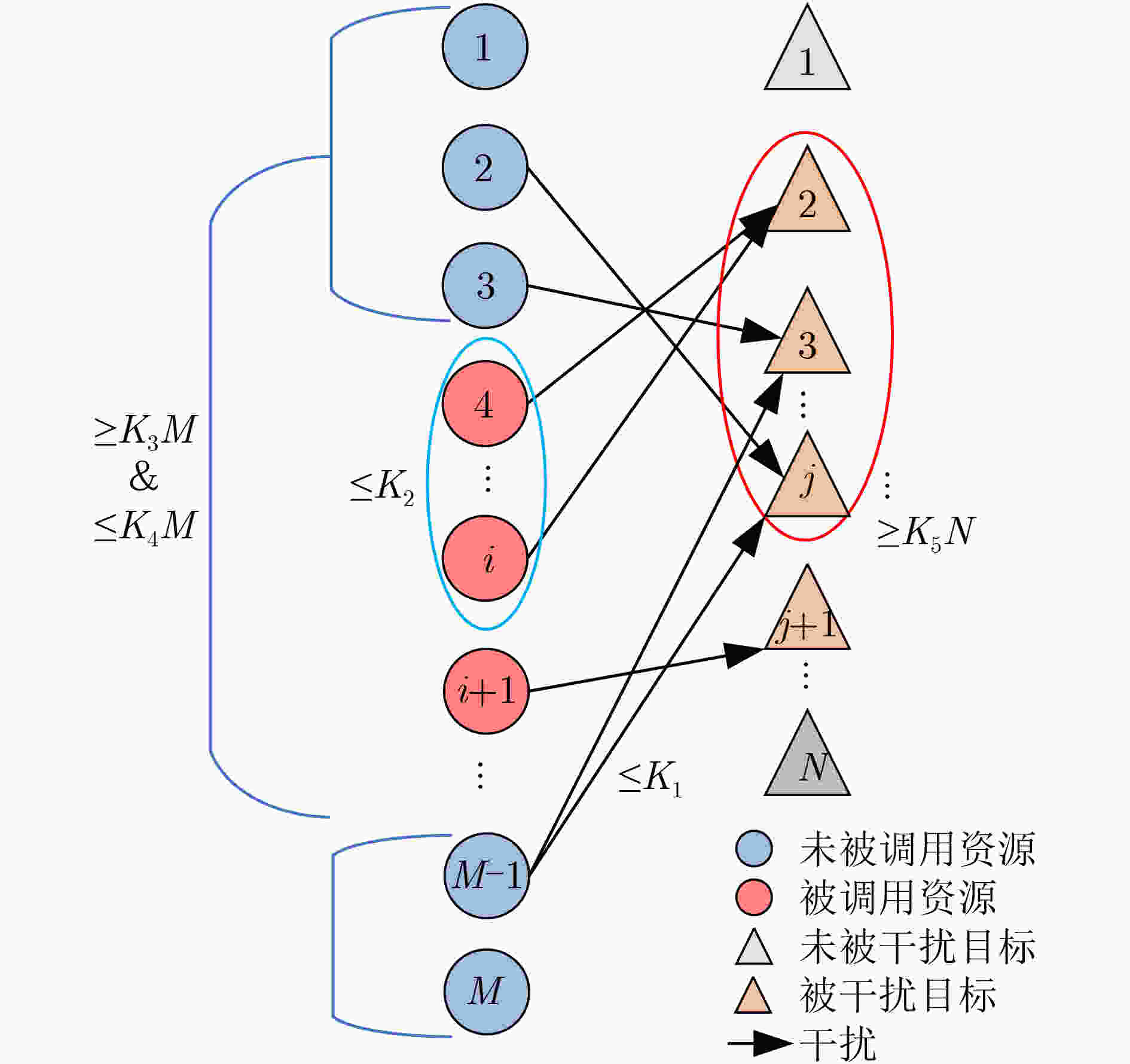
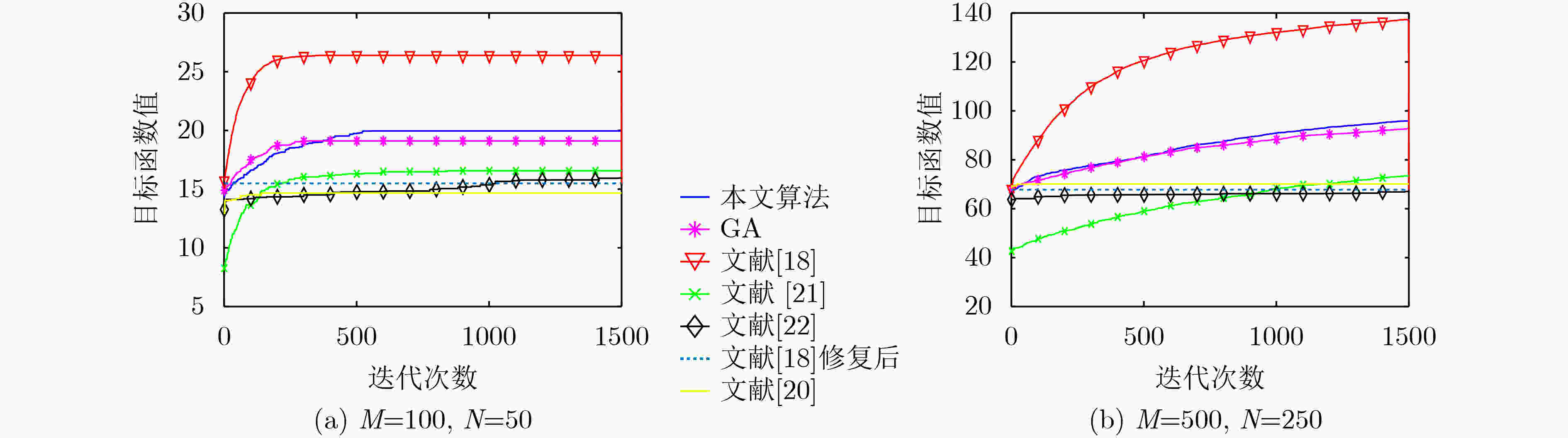
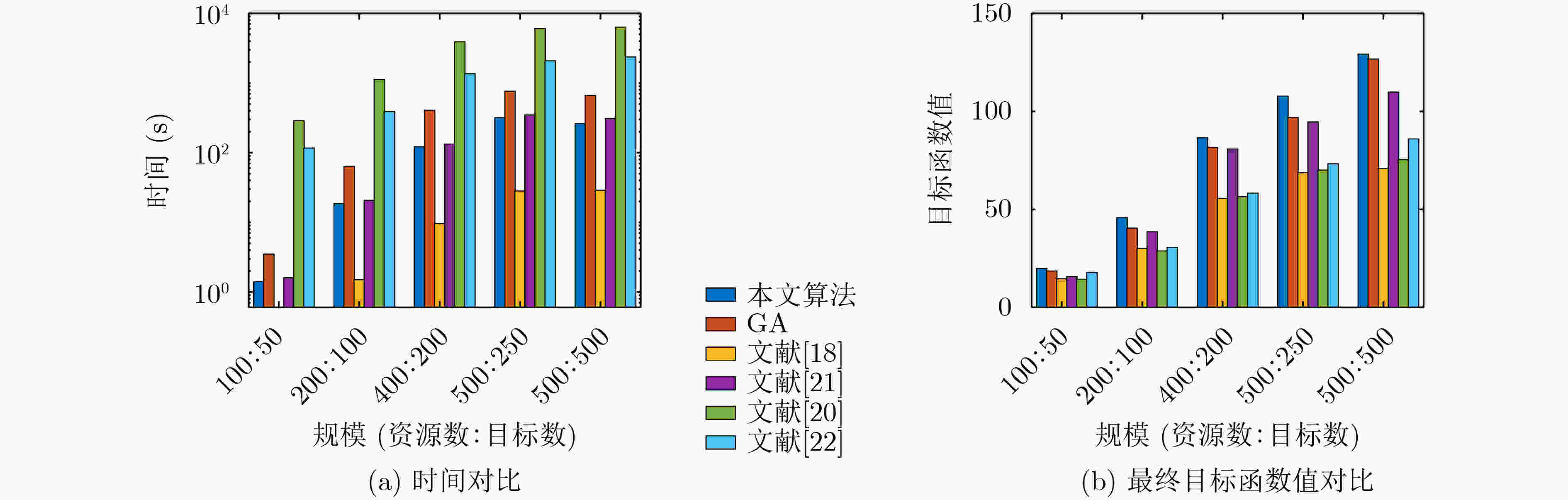
摘要: 在中大规模无人机干扰资源调度中，针对现有模型约束条件简单、调度算法适用规模较小的问题，该文提出了带最少任务数约束的资源调度模型，以最大化干扰效益和最小化成本为目标，用层次分析法对效益与成本指标赋权，并设计了一种用精英集加快收敛的改进并行遗传算法。在中等规模和500:500(干扰资源数:目标数)的更大规模仿真实验中，所提算法与遗传算法、非支配排序遗传算法II、修复遗传算法、基于岛屿模型的并行遗传算法和自适应模拟退火遗传禁忌搜索算法的性能相比，能在更短的时长内达到较优的目标函数值。
- 干扰对抗 /
- 资源调度 /
- 遗传算法 /
- 并行算法 /
- 混合模型
Abstract: In order to solve the optimization problem of jamming resource scheduling in medium and large-scale Unmanned Aerial Vehicle (UAV) jamming scenarios, a jamming resource scheduling model that can meet the minimum number of tasks constraint is proposed to improve the simple constraints and small-scale solution algorithms of the existing models. The interference benefit and cost indicators are weighted by the analytic hierarchy process. Then an improved parallel genetic algorithm is designed, where the elite set is introduced to accelerate the convergence of the algorithm. The simulation results in medium scale and larger scale jamming situations, such as 500:500 (number of jamming resources: number of targets) show that the proposed algorithm converges faster and achieves better objective function value than the existing representative and improved genetic algorithms.
- Interference countermeasure /
- Resource scheduling /
- Genetic algorithm /
- Parallel algorithm /
- Hybrid mode

HTML全文

1. 引言

随着科学技术的快速发展，探地雷达技术作为一种非侵入浅表地球物理探测技术，已在土建、环保与军事等诸多重要领域得以广泛应用^[1-5]。在对探地雷达系统电磁波束传播过程进行分析研究时，数值模拟是有效方法之一^[6]。近年来，针对探地雷达系统的建模与仿真分析，有不少研究工作先后提出了性能良好的数值模拟算法。时域有限差分法以其易于实现，且可以对色散、有损介质进行建模仿真而成为常用方法之一。在探地雷达系统工作过程中，由于其电磁脉冲特性参数会受到诸如传输介质介电特性等相关参数的影响，系统对探测目标或对象的测量精度受到不同程度影响。故而，在对探地雷达系统进行建模仿真时必须考虑模型输出结果对这些相关参数集(即模型中输入参数集)的依赖性。然而，在实际建模仿真中，由于对输入参数(如土壤的介电特性)缺乏精确的知识，模拟仿真输出结果中存在不确定性^[7]。为使模拟仿真结果更具现实指导价值，当考虑对输出结果置信度进行定量化表征时，针对探地雷达建模仿真进行不确定性分析就显得尤为必要^[8]。

不确定性分析法可分为两类：非嵌入式方法和嵌入式方法。传统的非嵌入式方法即为蒙特卡罗方法^[9]，该算法要求执行数千次仿真代码直到结果收敛，这势必会导致高额的计算成本。在目前已有的研究中^[8]，有学者提出了将广义多项式混沌展开应用到辅助微分方程时域有限差分(Auxiliary Differential Equation – Finite Difference Time Domain, ADE-FDTD)中的嵌入式不确定性分析方法来量化由不确定输入参数引起的输出结果的不确定性。该方法较蒙特卡罗方法在运算量与计算效率方面已取得了显著的性能提升。然而，这种方法亦有一定局限性，其主要缺陷表现在：其一，计算复杂度会随着输入不确定参数集维数增加而迅速增加，显然这对于输入不确定参数集维数较大的情况是不适用的；其二，广义多项式混沌展开通常在仿真模型输入参数变化不大的情况下，可得到的较理想的不确定分析结果。但是在输入参数变化较剧烈，引起数值仿真输出结果较大波动的情况下，该方法很可能达不到预期的结果。

为了有效解决上述问题，在探地雷达建模仿真不确定性分析研究过程中，本文构造了一种基于人工神经网络(Artificial Neural Network, ANN)的替代模型，该模型通过模拟替代探地雷达仿真模型的方式，可对系统参数不确定性进行分析与研究。考虑到在获取建立ANN替代模型所需训练、测试与验证数据样本时仍需运用基于ADE-FDTD进行全波仿真，文中首先阐述了探地雷达系统物理模型及其基于ADE-FDTD全波仿真计算的理论原理；其次，提出并设计基于ANN的替代模型，对构建替代模型过程中若干关键问题进行了详细分析与讨论，如激活函数^[10]的选择与比较分析、如何降低或抑制过拟合^[11]现象等；最后，为了验证ANN替代模型的准确性与有效性，结合探地雷达系统某一特定应用场景，利用ANN替代模型对系统输出结果进行预测，并与蒙特卡罗仿真(Monte Carlo Simulation, MCS)的结果进行比较分析。经数值模拟应用分析，基于ANN的替代模型所得预测结果与传统不确定性分析方法蒙特卡罗方法的结果达到较好的一致性，这使得探地雷达建模仿真输出结果不确定性分析过程摆脱运算量大、计算效率低下的困境。

2. 探地雷达系统建模与ADE-FDTD全波仿真原理

在建模中，土壤被认为是一种非磁性介质，其介电常数与频率有关，并且将其建模为具有静态电导率 ${\sigma _{\text{s}}}$ 的2维德拜模型。该模型相关参数均可由测量获得^[1]。然而，由于测量系统误差与偶然误差等测量误差的存在与影响，必然导致模型相关参数中均包含不确定性的成分。研究中，土壤介质材料相对介电常数 ${\varepsilon _{\rm{r}}}(\omega ,\theta )$ 由式(1)确定

${\varepsilon _{\rm{r}}}(\omega ,\theta ) = {\varepsilon _\infty }(\theta ) + \sum\limits_{p = 1}^2 {\frac{{({\varepsilon _{\rm{s}}}(\theta ) - {\varepsilon _\infty }(\theta )){A_p}(\theta )}}{{1 + {\rm{j}}\omega {\tau _p}(\theta )}}} + \frac{{{\sigma _{\rm{s}}}(\theta )}}{{{\rm{j}}\omega {\varepsilon _0}}}$

(1)

其中， ${\varepsilon _\infty }(\theta )$ 表示当角频率 $\omega$ 为无穷大时土壤介电常数， ${\varepsilon _{\rm{s}}}(\theta )$ 表示静态介电常数， ${A_p}(\theta )$ 表示极点振幅， ${\tau _p}(\theta )$ 表示弛豫时间， ${\varepsilon _0}$ 是自由空间中电介质常数， $\omega$ 是角频率， $\theta$ 为一随机变量， ${\rm{j}}$ 为虚数单位。假定相对介电常数 ${\varepsilon _{\rm{r}}}(\omega ,\theta )$ 表达式中如下7个参数： ${\varepsilon _\infty }(\theta )$ ， ${\varepsilon _{\rm{s}}}(\theta )$ ， ${A_1}(\theta )$ ， ${A_2}(\theta )$ ， ${\tau _1}(\theta )$ ， ${\tau _2}(\theta )$ 和 ${\sigma _{\text{s}}}(\theta )$ 为包含不确定性的输入参数。

2维空间中描述电磁波传播规律的麦克斯韦方程可由式(2)，式(3)，式(4)给出

$\qquad \frac{{\partial {H_x}}}{{\partial t}} = - \frac{1}{\mu }\frac{{\partial {E_z}}}{{\partial y}}$

(2)

$\qquad \frac{{\partial {H_y}}}{{\partial t}} = \frac{1}{\mu }\frac{{\partial {E_z}}}{{\partial x}}$

(3)

$\qquad \frac{{\partial {E_z}}}{{\partial t}} = \frac{1}{\varepsilon }\left(\frac{{\partial {H_y}}}{{\partial x}} - \frac{{\partial {H_x}}}{{\partial y}}\right)$

(4)

其中， ${H_x}$ 与 ${H_y}$ 分别表示x轴方向与y轴方向的磁场强度， ${E_z}$ 表示z轴方向电场强度， $\mu$ 为磁导率， $\varepsilon$ 为介电常数。

为采用ADE-FDTD方法分析色散介质中电磁波传播规律，沿z轴方向电场强度 ${E_z}$ 的第1辅助变量 ${L_z}(\omega ,\theta )$ 可表示为

${L_z}(\omega ,\theta ) = {\varepsilon _0}{\varepsilon _r}(\omega ,\theta )\frac{{{W_y}}}{{{W_z}}}{E_z}$

(5)

其中， ${W_y}$ 与 ${W_z}$ 分别与y，z法平面相关联，并且 ${W_h}$ 的函数形式由式(6)给出：

${W_h} = {s_h} + \frac{{{\sigma _h}}}{{{\text{j}}\omega {\varepsilon _0}}},\;h = x,y,z$

(6)

有关 ${s_h}$ 与 ${\sigma _h}$ 的详细说明可参阅Taflove等人论著^[6]。第2辅助变量 ${D_z}(\omega ,\theta )$ 可表示为

${D_z}(\omega ,\theta ) = {\varepsilon _r}(\omega ,\theta ){E_z}$

(7)

第3辅助变量 ${R_p}_z(\omega ,\theta )$ 可表示为

${R_p}_z(\omega ,\theta ) = {\text{j}}\omega \frac{{({\varepsilon _s}(\theta ) - {\varepsilon _\infty }(\theta )){A_p}(\theta )}}{{1 + {\text{j}}\omega {\tau _p}(\theta )}}{E_z}$

(8)

将式(5)，式(7)，式(8)代入ADE-FDTD更新方程，通过式(11)可解得沿z轴方向电场强度 ${E_z}$ 。在ADE-FDTD更新迭代过程中，3个辅助变量分别记为 $L_z^k({n_x},{n_y},\theta )$ ， $D_z^k({n_x},{n_y},\theta )$ ， $R_{pz}^k({n_x},{n_y},\theta )$ ，其具体函数形式由式(9)，式(10)，式(12)给出。式中n_x与n_y分别表示沿x，y轴方向上的空间步长，k为时间步长，Δx，Δy分别是沿x，y轴方向上的采样宽度，Δt是时间间隔。

$\begin{split} L_z^{k + 1}({n_x},{n_y},\theta ) =& \frac{{2{\varepsilon _0}{s_x} - {\sigma _x}\Delta t}}{{2{\varepsilon _0}{s_x} + {\sigma _x}\Delta t}}L_z^k({n_x},{n_y},\theta ) \\ &+ \frac{{2{\varepsilon _0}\Delta t}}{{2{\varepsilon _0}{s_x} + {\sigma _x}\Delta t}}\\ &\left[\frac{1}{{\Delta x}} \left(H_y^{k + \frac{1}{2}}\left({n_x} + \frac{1}{2},{n_y},\theta \right) \right.\right.\\ & \left.- H_y^{k + \frac{1}{2}}\left({n_x} - \frac{1}{2},{n_y},\theta \right)\right) \\ &- \frac{1}{{\Delta y}} \left(H_x^{k + \frac{1}{2}}\left({n_x},{n_y} + \frac{1}{2},\theta \right) \right.\\ & \left.\left.- H_x^{k + \frac{1}{2}}\left({n_x},{n_y} - \frac{1}{2},\theta \right)\right)\right] \end{split}$

(9)

$\begin{split} D_z^{k + 1}({n_x},{n_y},\theta ) =& \frac{{2{\varepsilon _0}{s_y} - {\sigma _y}\Delta t}}{{2{\varepsilon _0}{s_y} + {\sigma _y}\Delta t}}D_z^k({n_x},{n_y},\theta ) \\ &+ \frac{2}{{2{\varepsilon _0}{s_y} + {\sigma _y}\Delta t}} \\ & \cdot (L_z^{k + 1}({n_x},{n_y},\theta ) - L_z^k({n_x},{n_y},\theta )) \\ \end{split}$

(10)

$\begin{split} & E_z^{k + 1}({n_x},{n_y},\theta )\\ & \quad=\frac{{{C_1}}}{C}E_z^k({n_x},{n_y},\theta ) \\ & \qquad- \frac{{4{\varepsilon _0}\Delta t{\tau _1}(\theta )(2{\tau _2}(\theta ) + \Delta t)}}{C}R_{1z}^k({n_x},{n_y},\theta ) \\ & \qquad -\frac{{4{\varepsilon _0}\Delta t{\tau _2}(\theta )(2{\tau _1}(\theta ) + \Delta t)}}{C}R_{2z}^k({n_x},{n_y},\theta ) \\ & \qquad+ \frac{{2{\varepsilon _0}(2{\tau _1}(\theta ) + \Delta t)(2{\tau _2}(\theta ) + \Delta t)}}{C} \\ & \qquad \cdot(D_z^{k + 1}({n_x},{n_y},\theta ) - D_z^k({n_x},{n_y},\theta )) \end{split}$

(11)

$\begin{split} R_{pz}^{k + 1}({n_x},{n_y},\theta ) =& \frac{{2{\tau _p}(\theta ) - \Delta t}}{{2{\tau _p}(\theta ) + \Delta t}}R_{pz}^k({n_x},{n_y},\theta )\\ &+ \frac{{2({\varepsilon _s}(\theta ) - {\varepsilon _\infty }(\theta )){A_p}(\theta )}}{{2{\tau _p}(\theta ) + \Delta t}} \\ & \cdot(E_z^{k + 1}({n_x},{n_y},\theta ) - E_z^k({n_x},{n_y},\theta ) \end{split}$

(12)

式中，

$\begin{split} \; C =& (2{\varepsilon _0}{\varepsilon _\infty }(\theta ) + {\sigma _s}(\theta )\Delta t)(2{\tau _1}(\theta ) + \Delta t) \\ &(2{\tau _2}(\theta ) + \Delta t) +2{\varepsilon _0}\Delta t({\varepsilon _s}(\theta ) - {\varepsilon _\infty }(\theta ))\\ &({A_1}(\theta )(2{\tau _2}(\theta ) + \Delta t) + {A_2}(\theta )(2{\tau _1}(\theta ) + \Delta t)) \end{split}$

$\begin{split} \;{C_1} =& (2{\varepsilon _0}{\varepsilon _\infty }(\theta ) - {\sigma _s}(\theta )\Delta t)(2{\tau _1}(\theta ) + \Delta t) \\ &(2{\tau _2}(\theta ) + \Delta t) + 2{\varepsilon _0}\Delta t({\varepsilon _s}(\theta ) - {\varepsilon _\infty }(\theta )) \\ &({A_1}(\theta )(2{\tau _2}(\theta ) + \Delta t) + {A_2}(\theta )(2{\tau _1}(\theta ) + \Delta t)) \end{split}$

同理，可得到沿x，y轴方向上的磁场强度 ${H_x}$ 与 ${H_y}$ 。ADE-FDTD更新方程表明，土壤模型参数的不确定性会引入 ${H_x}$ ， ${H_y}$ 和 ${E_z}$ 数值仿真结果的不确定性。因此，为使模拟仿真结果更具现实指导意义，对输出结果中的不确定性进行量化分析就显得尤为必要。本文基于ANN技术，设计构造ANN替代模型模拟替代探地雷达仿真模型。

3. 人工神经网络(ANN)替代模型的构建

3.1 ANN替代模型设计

基于ANN的替代模型旨在对任意给定一组包含不确定性的输入参数时，能够准确预测探地雷达系统的输出结果，其训练过程与测试过程如图1所示。

图 1 ANN替代模型的训练过程与测试过程

下载: 全尺寸图片幻灯片

如图1(a)所示，在该模型训练过程中，包含不确定性的土壤介电特性参数矩阵 ${\boldsymbol{I}}=\left\{ {{{\boldsymbol{I}}}}_{1}\;{{{\boldsymbol{I}}}}_{2} \;\cdots\; {{{\boldsymbol{I}}}_{M}}\right\}$ ( ${ {{\boldsymbol{I}}} _m} \in {\mathbb{R}^S}$ ， $1 \le m \le M$ 表示某一S维空间向量)与FDTD全波仿真输出结果 ${\boldsymbol{U}}=\left\{{{{\boldsymbol{U}}}}_{1}\;{{{\boldsymbol{U}}}}_{2}\;\cdots \;{{{\boldsymbol{U}}}_{M}}\right\}$ ( ${ {{\boldsymbol{U}}} _m} \in {\mathbb{R}^D}$ ， $1 \le m \le {M}$ 表示某一D维空间向量)构成训练样本，其中M为训练集样本个数。在图1(b)模型测试过程中，当给定一组新的不确定性输入参数集 ${\boldsymbol{I}}=\left\{{{{\boldsymbol{I}}}}_{1}\;{{{\boldsymbol{I}}}}_{2}\;\cdots \;{{{\boldsymbol{I}}}}_{N}\right\}$ 时，使用已经训练好的ANN替代模型可得到对应于新不确定性输入参数集I的全波仿真输出结果的预测值 ${{\boldsymbol{U}}}^{\prime }=\left\{{{{\boldsymbol{U}}}}'_{1}\;{{{\boldsymbol{U}}}}'_{2}\;\cdots \;{{{\boldsymbol{U}}}}'_{N}\right\}$ ( ${ {{\boldsymbol{U}}} '_n} \in {\mathbb{R}^D}$ ， $1 \le n \le N$ 表示某一D维空间向量)。基于此设计思路，探地雷达系统建模仿真的不确定分析研究过程便可通过运行此替代模型，得到其仿真结果的统计特征(如均值、标准差等)，而不是重复数以千次地运行ADE-FDTD全波仿真。

在本研究设计中，神经网络的数据集分为3个部分：训练集、测试集和验证集。其中，训练数据集占全部数据的60%。模型参数均采用一种基于低阶矩估计的随机目标函数一阶梯度优化算法，即自适应矩估计(Adam)算法^[12]，进行优化处理。

3.2 激活函数的选择与性能比较分析以及抑制过拟合策略

在ANN替代模型超参数的选择与设计上，考虑到ANN隐藏层激活函数对模型的学习能力与预测精度有重要影响，文中针对当前几种主流ANN激活函数，如ReLU(Rectified Linear Unit)函数^[13]、LReLU(Leaky Rectified Linear Units)函数^[14]、PReLU(Parametrized Rectified Linear Units)函数^[15]以及ELU(Exponential Linear Unit)函数^[16]，分别将其应用于ANN替代模型隐藏层，并分析比较它们对ANN整体性能的影响。

其中，ReLU函数的具体函数形式如式(13)

$f({a_i}) = \left\{ \begin{aligned} & 0,{\text{ }}{a_i} < 0 \hfill \\ & {a_i},{\text{ }}{a_i} \ge 0 \hfill \\ \end{aligned} \right.$

(13)

LReLU函数的具体函数形式如式(14)

$f({a_i}) = \left\{ \begin{aligned} & \alpha {a_i},{\text{ }}{a_i} < 0 \hfill \\ & {a_i},{\text{ }}{a_i} \ge 0 \hfill \\ \end{aligned} \right.$

(14)

PReLU函数的具体函数形式如式(15)

$f({a_i}) = \left\{ \begin{aligned} & {\alpha _i}{a_i},{\text{ }}{a_i} < 0 \hfill \\ & {a_i},{\text{ }}{a_i} \ge 0 \hfill \\ \end{aligned} \right.$

(15)

ELU函数的具体函数形式如式(16)

$f({a_i}) = \left\{ \begin{aligned} & \alpha (\exp ({a_i}) - 1),{\text{ }}{a_i} < 0 \hfill \\ & {a_i},{\text{ }}{a_i} \ge 0 \hfill \\ \end{aligned} \right.$

(16)

式(13)—式(16)中 ${a_i}$ 表示第i个神经元的输入， $\alpha$ 是超参数，而 ${\alpha _i}$ 是一可学习参数。此外，对于ANN输入输出层的激活函数则选取ReLU函数。ANN性能评价采用均方差(MSE)公式进行，如式(17)

${\rm{MSE}} = \frac{1}{R}\sum\limits_{r = 1}^R {{{({Y_r} - {{\hat Y}_r})}^2}}$

(17)

其中， ${Y_r}$ 与 ${\hat Y_r}$ 分别表示第r个数据的观测值与预测值，R表示数据的总个数。

当分别将ReLU函数、LReLU函数、PReLU函数与ELU函数应用于ANN替代模型隐藏层后，经过对模型进行反复训练学习，得出不同激活函数作用下ANN替代模型的训练损失函数和验证损失函数随Epochs的变化规律，如图2所示。

图 2 4种不同激活数属分别应用于ANN替代模型隐藏层后训练损失函数与验证损失函数随Epochs的变化关系(未应用DropOut方法)

下载: 全尺寸图片幻灯片

从图2可以看出，除应用ELU函数外，选择将其余3种函数作为ANN隐藏层激活函数时，ANN均产生较大程度的过拟合问题。为此，研究中针对选取ReLU函数、PReLU函数和LReLU函数作为隐藏层激活函数的ANN在其训练过程中分别应用DropOut方法来抑制过拟合问题。DropOut方法的核心思想如式(18)—式(21)所述^[16]

$\qquad\qquad r_i^g\sim{\text{Bernoulli}}(q)$

(18)

$\qquad\qquad {{\boldsymbol{\tilde y}}^g} = {{\boldsymbol{r}}^g} * {{\boldsymbol{y}}^g}$

(19)

$\qquad\qquad a_i^{g + 1} = w_i^{g + 1}{{\boldsymbol{\tilde y}}^g} + b_i^{g + 1}$

(20)

$\qquad\qquad y_i^{g + 1} = f(a_i^{g + 1})$

(21)

其中， ${{\boldsymbol{a}}^g}$ 表示第g层网络输入矢量， ${{\boldsymbol{y}}^g}$ 表示第g层网络输出矢量， ${{\boldsymbol{\tilde y}}^g}$ 表示对第g层应用DropOut方法之后对应的输出矢量， ${{\boldsymbol{w}}^g}$ 和 ${{\boldsymbol{b}}^g}$ 分别表示第g层的权重与偏置， $*$ 表示矢量内积，f表示激活函数。对ANN中任意隐藏层g， ${{\boldsymbol{r}}^g}$ 为一随机矢量，由相互独立的若干伯努利随机变量组成，且每个随机变量的概率q为1。

针对前述应用ReLU函数、PReLU函数和LReLU函数作为隐藏层激活函数而产生过拟合问题的ANN网络，对其分别应用DropOut方法，经过模型训练与学习，使用DropOut方法能够显著地抑制ANN网络的过拟合问题。表1分别给出了应用DropOut方法前后，选择不同函数作为隐藏层激活函数时，ANN替代模型在经过5000次迭代之后的训练数据与验证数据的损失值情况。

表 1 应用DropOut方法前后，不同激活函数作用时ANN替代模型的损失函数值

激活函数	网络是否应用 DropOut方法	训练数据损失 (×10^–5)	验证数据损失 (×10^–5)
ReLU函数	否	0.763	6.98
ReLU函数	是	3.730	4.28
LReLU函数	否	2.780	5.50
LReLU函数	是	3.720	4.36
PReLU函数	否	0.953	7.65
PReLU函数	是	3.730	4.30
ELU函数	否	3.740	4.30
ELU函数	是	/	/

下载: 导出CSV

| 显示表格

通过对表1进行比较分析，不难发现如下结论：(1)相较于ReLU函数、LReLU函数和PReLU函数，选取ELU函数作为ANN替代模型隐藏层激活函数时，其在替代模型训练过程中能够在一定程度上改善过拟合问题，并且模型收敛速度更快；(2)针对前三者作为隐藏层激活函数时替代模型存在过拟合的问题，若对替代模型的隐藏层应用DropOut方法，可显著改善训练数据过拟合的问题。

4. 仿真与结果

4.1 模型描述

图3给出了本文所研究探地雷达系统及其具体应用场景在进行ADE-FDTD全波仿真时的2维模型。如图所示，一块边长为1 m的正方形金属目标物埋置于色散土壤内，且在其旁边存在一边长为0.5 m的干燥花岗岩。图中 ${T_x}$ 与 ${R_x}$ 分别表示发射机与接收机，其均被建模为点源^[17-19]。研究采用Blackmann-Harris脉冲作为激励源脉冲。其中，中心频率f_c=200 MHz，T_s=1.55/f_c。同时，将各向异性完全匹配层(Uniaxial Perfectly Matched Layer，UPML)作为吸收边界条件。

图 3 探地雷达系统及其应用场景模拟模型

下载: 全尺寸图片幻灯片

模拟计算中，模型计算域为xoy平面内x × y = 4.00 m × 4.00 m的区域，并且将其分解为方形单元网格。空间采样宽度Δx = Δy = $\varDelta$ = 5.00 mm。时间步长Δt = Δx/(2c) = 8.33 ps，式中c表示自由空间中的光速。UPML的厚度是10 $\varDelta$ 。德拜模型的相关参数均通过测量得到，各参数中均含有不确定性成分，如表2所示。

表 2 色散土壤模型参数

土壤湿度(%)	${\varepsilon _\infty }$	${\sigma _{\text{s}}}$ （mS/m）	${A_1}$	${A_2}$	${\tau _1}$ （ns）	${\tau _1}$ （ns）
2.5	3.20	0.397	0.75	0.30	2.71	0.108
5	4.15	1.110	1.80	0.60	3.79	0.151
10	6.00	2.000	2.75	0.75	3.98	0.251

下载: 导出CSV

| 显示表格

图4给出了当包含不确定性的输入参数个数为7时，采用MCS方法，在2维探地雷达模型接收机 ${R_x}$ 处观测得到电场强度 ${E_z}$ 随时间变化的规律。该曲线基于60个采样点绘制而成，且模拟中每个输入参数的不确定性变化范围为10%。从电场强度 ${E_z}$ 的变化规律曲线中亦可以看出，输入参数中的不确定性会致使模拟输出结果中产生不确定性成分。与已有研究成果^[8]相比较，本研究将输入参数的变化范围从5%提高到10%，较大的不确定输入参数的变化范围会引起输出相对更大的不确定性，增大了不确定性分析的难度。

图 4 基于MCS方法的电场强度

${E_z}$ 变化规律

下载: 全尺寸图片幻灯片

研究中，色散土壤湿度取2.5%，干燥花岗岩的相对介电常数 ${\varepsilon _g}$ 为5，电导率 ${\sigma _g}$ 为10^–5mS/m。所有数值模拟计算过程均由一台处理器为Intel i5-6440HQ，主频2.6GHz，内存为16GB的计算机完成。执行一次全波仿真的CPU用时为1098.80 s。

4.2 ANN替代模型超参数

研究中在ANN替代模型运用之前，FDTD仿真模拟中输入输出值均对其进行标准化处理。同时，采用拉丁超立方采样法(LHS)获取模型输入参数。此外，对于ANN替代模型的Batch size参数、隐藏层数量，以及各隐藏层内神经元数量等其它超参数的设置如表3所示。

表 3 ANN替代模型超参数设置

神经网络	Batch Size	Epochs数量	隐藏层数量及各层神经元数量
ANN替代模型	25	5000	1000，1000，1000

下载: 导出CSV

| 显示表格

4.3 基于ANN替代模型的探地雷达系统输出结果不确定性分析

当ANN替代模型完成训练学习过程后，其即可被用来对探地雷达系统输出结果进行预测，并进一步用于不确定性分析中。图5给出了基于ANN替代模型对接收机 ${R_x}$ 处电场强度 ${E_z}$ 的预测值进行统计计算得到 ${E_z}$ 的均值与标准差变化规律。

图 5 土壤中含有金属块以及花岗岩，输入不确定性参数个数为7且变化波动范围均为10%时，

${R_x}$ 处电场强度

${E_z}$ 统计特性

下载: 全尺寸图片幻灯片

从图5可以看出，当ANN替代模型隐藏层激活函数采用ELU函数时所得结果与基于ADE-FDTD的全波仿真所得结果，无论是均值还是方差都具有较好的一致性。与此同时，从图5也可以发现，当ANN替代模型隐藏层激活函数分别采用ReLU函数、LReLU函数、 PReLU函数并应用DropOut方法的3种结果基本相似，所得方差与全波仿真的结果有一定偏差。当与图6进行对比分析会发现，分别采用ReLU函数、LReLU函数、PReLU函数作为ANN隐藏层激活函数，且不应用DropOut 方法减少过拟合时，得到的方差与全波仿真所得方差的偏差进一步增大。综上所述，采用ELU函数可以得到较好的预测结果，并且无需考虑过拟合问题。

图 6 土壤中含有金属块以及花岗岩，输入不确定性参数个数为7且变化波动范围均为10%时，

${R_x}$ 处电场强度

${E_z}$ 统计特性

下载: 全尺寸图片幻灯片

表4给出了分别采用传统MCS不确定分析法和ANN替代模型(ELU函数作为激活函数)进行数值模拟的CPU耗时情况。其中，ANN替代模型的数值模拟CPU耗时主要由两部分组成：(1)替代模型训练学习耗时(2011.21 s)；(2)任给一组新输入参数，替代模型预测1000个输出结果的耗时(1.80 s)。

表 4 传统MCS不确定分析法和ANN替代模型进行数值模拟的CPU耗时

数值模拟方法	仿真次数	CPU耗时(s)
MCS	1000	1125663.71
ANN替代模型	200	2011.21(训练耗时)+1.80(预测耗时)

下载: 导出CSV

| 显示表格

从表4可以看出，在结果保持较好一致性的情况下，采用ANN替代模型极大地减少了ADE-FDTD仿真次数，并且计算效率更高。需要注意的是，尽管ANN的训练时间以及预测时间较短，但是为了得到训练样本进行200次全波仿真也需要消耗时间。

4.4 ANN替代模型的适应性分析与验证

为了进一步研究分析ANN替代模型对GPR系统数值模拟模型中异常体数量、类型、分布形态、介电参数等参数变化的适应性与有效性，研究去除了图3所示模型中的干燥花岗岩，仅保留正方形金属目标物，并将其边长由1 m减小至0.3 m，其他数值模型参数条件保持不变。同时，模型输入不确定性参数个数仍为7个，且随机波动变化范围也为10%。图7给出了基于ANN替代模型对接收机 ${R_x}$ 处电场强度 ${E_z}$ 的预测值进行统计计算得到 ${E_z}$ 的均值与标准差变化规律。在这里，ANN替代模型隐藏层激活函数直接采用ELU函数。从图7所示模型预测结果的统计特性曲线可以看出，即使系统模拟模型变化，GPR系统回波时域波形发生改变，本文提出的ANN替代模型预测结果的统计特性依然可以与MCS不确定分析法所得结果保持较好一致。

图 7 土壤中含有金属块，输入不确定性参数个数为7且变化波动范围均为10%时，

${R_x}$ 处电场强度

${E_z}$ 统计特性

下载: 全尺寸图片幻灯片

5. 结论

本文旨在对2维探地雷达系统建模仿真中因色散有损土壤介质的不确定性参数所引起的仿真输出结果的不确定性量化分析方法进行研究。针对传统不确定性分析方法解决此类问题时计算效率低、运算量大的问题，提出了一种基于ANN的替代模型，替代探地雷达系统全波仿真行为的方式，基于该模型方法可对探地雷达系统输出结果进行预测，进而得到输出结果统计特性以进行有效的参数不确定性分析。其次，文中对构建ANN替代模型的关键问题，如隐藏层激活函数的选择、如何抑制过拟合现象等，进行了详细的比较分析。结果显示：相较于ReLU函数、LReLU函数与PReLU函数，选择ELU函数作为替代模型隐藏层激活函数可获得较为理想的网络性能。当选取前三者作为隐藏层激活函数时，替代模型将会产生明显的过拟合问题，为此可采用DropOut方法来抑制过拟合问题。最后，经具体应用案例模拟仿真验证分析，在相同的数值模型、不确定性输入参数个数，以及参数变化范围为10%的前提条件下，通过ANN替代模型所得不确定性分析结果与传统基于MCM法所得结果具有较好的一致性，且相较于后者，前者计算时间效率提升79.82%。本文的不足之处是土壤模型较为简单假设为均匀介质，没有考虑土壤的孔隙率等因素，在将来的工作中将完善仿真模型，考虑现实应用中的真实情况进行非均匀介质建模仿真。尽管ANN的训练时间以及预测时间相对MCS较短，但是为了得到ANN的训练样本，仍然耗时进行200次全波仿真。未来的工作将考虑如何减少ANN所需训练样本数，进一步减少时间消耗，提高效率。

图 1 干扰关系

下载: 全尺寸图片幻灯片

图 2 混合主-从和岛屿模型结构

下载: 全尺寸图片幻灯片

图 3 中、大规模资源调度优化目标函数值迭代趋势对比

下载: 全尺寸图片幻灯片

图 4 算法收敛性能对比(100次仿真平均)

下载: 全尺寸图片幻灯片

图 5 干扰资源与目标的空间位置

下载: 全尺寸图片幻灯片

图 6 中规模资源调度优化的目标函数值迭代趋势对比

下载: 全尺寸图片幻灯片

表 1 基于混合模型的并行遗传算法(算法1)

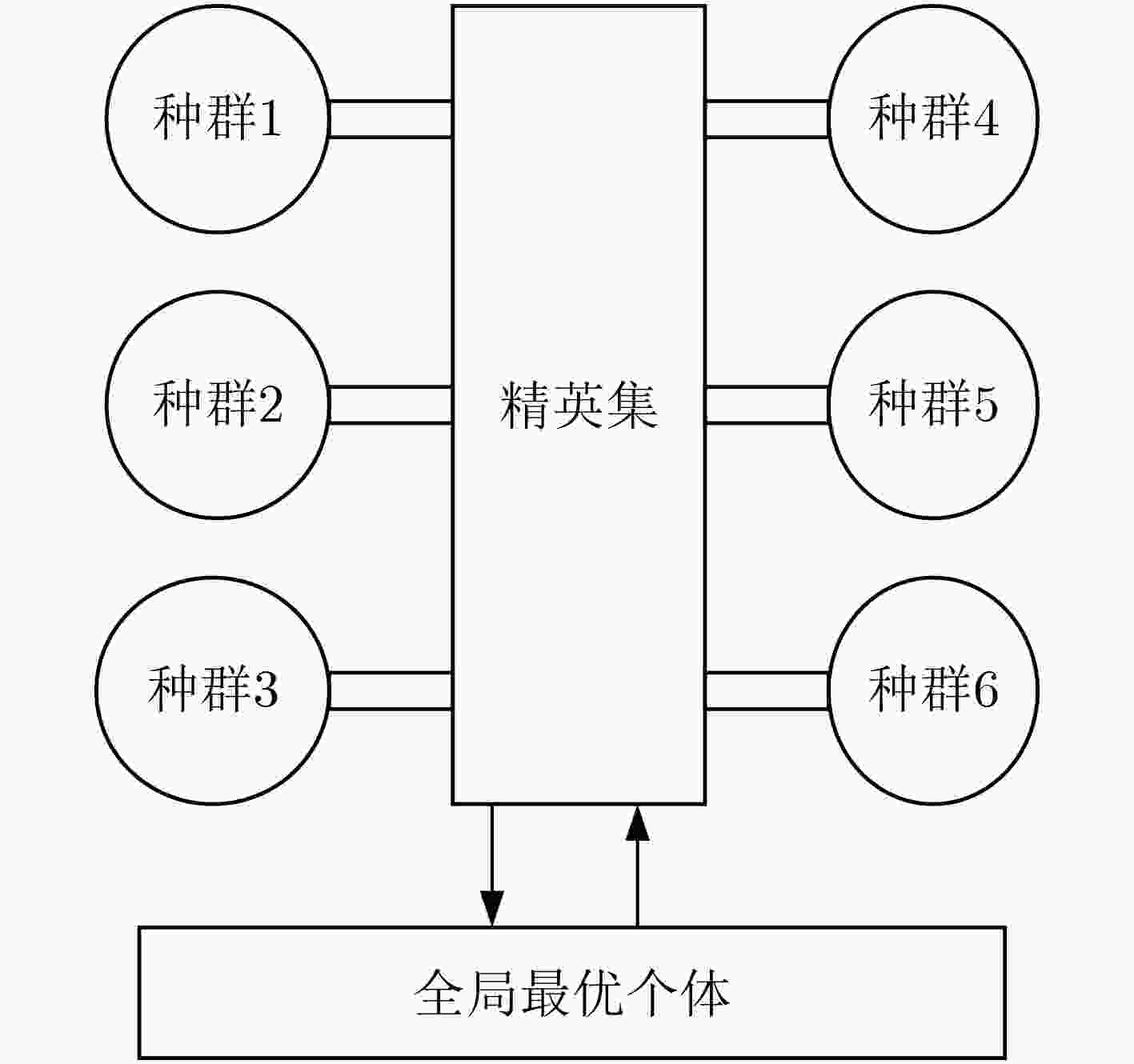
　1：　t=1// 迭代次数

　2：计算总干扰效益矩阵E，规模为M×N

　3：初始化S个子种群(pop₁,pop₂,···,pop_s)，种群规模为P，设置
　　每个子种群的最差个体g_1k，全局最优个体b₀;//

$S \ge 3$ ，根据
　　算法计算最短时间和并行线程而定；

　4：while(t<t_max)

　5：parfors=1:S;//S个子种群并行计算

　6：(pop_k,g_k,g_1k)=cacaulation(pop_k);//子种群进行选择，交叉，
　　变异等遗传操作，并计算操作后的目标函数值，选出最优个
　　体g_k,和最差个体g_1k，k=1,2,···,S

　7：end parfor

　8：G=(g₁,g₂,···,g_k);//k=1,2,···,S

　9：b₁=max(G)

　10：if b₁>b₀

　11：b₀=b₁;

　12：end if

　13：for k=1:S

　14：pop_k=change(g_1k,b₀,pop_k)//所有子种群将最差个体g_1k替换
　　为b₀

　15：end for

　16：end while

下载: 导出CSV

表 2 迭代1500次所用时间/最终目标函数值对比(100次仿真平均值)

算法	对抗规模
	100:50		200:100		400:200		500:250		500:500
	耗时(s)	函数值	耗时(s)	函数值	耗时(s)	函数值	耗时(s)	函数值	耗时(s)	函数值
本文算法	3.61	19.87	12.16	42.01	44.66	81.13	69.74	97.27	69.94	120.35
GA	9.84	18.56	37.95	37.85	101.03	76.82	217.29	92.06	212.15	121.03
文献[18]	1.83	14.63	2.42	30.13	3.65	55.34	4.11	67.65	4.20	68.36
文献[21]	5.42	15.72	13.82	36.79	54.42	74.33	78.12	90.80	80.67	98.19
文献[20]	287.60	14.38	1126.33	28.82	3912.38	56.50	6054.23	70.09	6343.78	75.40
文献[22]	13.57	15.71	53.01	28.67	219.72	54.54	300.68	67.34	310.36	68.93

下载: 导出CSV

表 3 在M=12, N=6规模下各算法在100次计算中取得最优解次数的百分比

算法	本文算法	GA	文献[18]	文献[21]	文献[20]	文献[22]
百分比(%)	96	41	24	80	0	4

下载: 导出CSV

参考文献(25)

[1]	AILIYA, YI Wei, and YUAN Ye. Reinforcement learning-based joint adaptive frequency hopping and pulse-width allocation for radar anti-jamming[C]. Proceedings of 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 2020: 1–6.
[2]	赵太飞, 宫春杰, 张港, 等. 一种无人机集群安全高效的分区集结控制策略[J]. 电子与信息学报, 2021, 43(8): 2181–2188. doi: 10.11999/JEIT200601 ZHAO Taifei, GONG Chunjie, ZHANG Gang, et al. A safe and high efficiency control strategy of unmanned aerial vehicles partition rendezvous[J]. Journal of Electronics &Information Technology, 2021, 43(8): 2181–2188. doi: 10.11999/JEIT200601
[3]	石荣, 刘江. 干扰资源分配问题的智能优化应用研究综述[J]. 电光与控制, 2019, 26(10): 54–61. doi: 10.3969/j.issn.1671-637X.2019.10.012 SHI Rong and LIU Jiang. Application of intelligent optimization methods in jamming resource allocation: A review[J]. Electronics Optics &Control, 2019, 26(10): 54–61. doi: 10.3969/j.issn.1671-637X.2019.10.012
[4]	JIANG Haiqing, ZHANG Yangrui, and XU Hongyi. Optimal allocation of cooperative jamming resource based on hybrid quantum-behaved particle swarm optimisation and genetic algorithm[J]. IET Radar, Sonar & Navigation, 2017, 11(1): 185–192. doi: 10.1049/iet-rsn.2016.0119
[5]	张阳, 司光亚, 王艳正. 无人机集群网电攻击行动协同目标分配建模[J]. 系统工程与电子技术, 2019, 41(9): 2025–2033. doi: 10.3969/j.issn.1001-506X.2019.09.15 ZHANG Yang, SI Guangya, and WANG Yanzheng. Modeling of cooperative target allocation of the UAV swarm cyberspace attack action[J]. Systems Engineering and Electronics, 2019, 41(9): 2025–2033. doi: 10.3969/j.issn.1001-506X.2019.09.15
[6]	OU Jian, ZHAO Feng, AI Xiaofeng, et al. Quantitative evaluation for self-screening jamming effectiveness based on the changing characteristics of intercepted radar signals[C]. Proceedings of 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 2016: 1–5.
[7]	YE Fang, CHE Fei, and GAO Lipeng. Multiobjective cognitive cooperative jamming decision-making method based on Tabu search-artificial bee colony algorithm[J]. International Journal of Aerospace Engineering, 2018, 2018: 7490895. doi: 10.1155/2018/7490895
[8]	张养瑞, 高梅国, 罗皓月, 等. 基于检测概率的雷达网协同干扰效果评估方法[J]. 系统工程与电子技术, 2015, 37(8): 1778–1786. doi: 10.3969/j.issn.1001-506X.2015.08.10 ZHANG Yangrui, GAO Meiguo, LUO Haoyue, et al. Evaluation method of cooperative jamming effect on radar net based on detection probability[J]. Systems Engineering and Electronics, 2015, 37(8): 1778–1786. doi: 10.3969/j.issn.1001-506X.2015.08.10
[9]	ZHAO Ming, ZHAO Lingling, SU Xiaohong, et al. Improved discrete mapping differential evolution for multi-unmanned aerial vehicles cooperative multi-targets assignment under unified model[J]. International Journal of Machine Learning and Cybernetics, 2017, 8(3): 765–780. doi: 10.1007/s13042-015-0364-3
[10]	段先华, 孙庆国, 蔡丹. 基于改进遗传算法的协同干扰资源优化分配[J]. 江苏科技大学学报:自然科学版, 2016, 30(5): 466–472. doi: 10.3969/j.issn.1673-4807.2016.05.011 DUAN Xianhua, SUN Qingguo, and CAI Dan. Optimization assignment for cooperative jamming resources based on improved genetic algorithms[J]. Journal of Jiangsu University of Science and Technology:Natural Science Edition, 2016, 30(5): 466–472. doi: 10.3969/j.issn.1673-4807.2016.05.011
[11]	GAO Xiangqiang, LIU Rongke, and KAUSHIK A. Hierarchical multi-agent optimization for resource allocation in cloud computing[J]. IEEE Transactions on Parallel and Distributed Systems, 2021, 32(3): 692–707. doi: 10.1109/TPDS.2020.3030920
[12]	韩鹏, 张龙. 雷达干扰资源优化分配博弈模型和算法[J]. 现代雷达, 2019, 41(2): 78–83,90. doi: 10.16592/j.cnki.1004-7859.2019.02.018 HAN Peng and ZHANG Long. Game model and algorithm of Radar jamming resources optimization allocation[J]. Modern Radar, 2019, 41(2): 78–83,90. doi: 10.16592/j.cnki.1004-7859.2019.02.018
[13]	YIN Changsheng, YANG Ruopeng, ZHU Wei, et al. Research on Radio frequency assignment method based on improved genetic algorithm[C]. Proceedings of the 2nd International Conference on Artificial Intelligence and Big Data (ICAIBD), Chengdu, China, 2019: 358–361.
[14]	YANG Jiao. Research on optimized reconfiguration of distributed distribution network based on ant colony optimization algorithm[C]. Proceedings of 2020 International Conference on Computer Engineering and Application (ICCEA), Guangzhou, China, 2020: 20–23.
[15]	YU V F, QIU Meng, PAN He, et al. An improved immunoglobulin-based artificial immune system for the aircraft scheduling problem with alternate aircrafts[J]. IEEE Access, 2021, 9: 16532–16545. doi: 10.1109/ACCESS.2021.3051971
[16]	WANG Xiangtuan, HUANG Tianyao, and LIU Yimin. Resource allocation for random selection of distributed jammer towards multistatic Radar system[J]. IEEE Access, 2021, 9: 29048–29055. doi: 10.1109/ACCESS.2021.3053762
[17]	许华, 宋佰霖, 蒋磊, 等. 一种通信对抗干扰资源分配智能决策算法[J]. 电子与信息学报, 2021, 43(11): 3086–3095. doi: 10.11999/JEIT210115 XU Hua, SONG Bailin, JIANG Lei, et al. An intelligent decision-making algorithm for communication countermeasure jamming resource allocation[J]. Journal of Electronics &Information Technology, 2021, 43(11): 3086–3095. doi: 10.11999/JEIT210115
[18]	XUE Y, ZHUANG Y, NI Q T, et al. One improved genetic algorithm applied in the problem of dynamic jamming resource scheduling with multi-objective and multi-constraint[C]. Proceedings of the IEEE 5th International Conference on Bio-Inspired Computing: Theories and Applications (BIC-TA), Changsha, China, 2010: 708–712.
[19]	GONG Yuejiao, CHEN Weineng, ZHAN Zhihui, et al. Distributed evolutionary algorithms and their models: A survey of the state-of-the-art[J]. Applied Soft Computing, 2015, 34: 286–300. doi: 10.1016/j.asoc.2015.04.061
[20]	DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182–197. doi: 10.1109/4235.996017
[21]	KIZIL A and KARABULUT K. Effects of parameters of an island model parallel genetic algorithm for the quadratic assignment problem[C]. Proceedings of the 8th International Congress on Advanced Applied Informatics (IIAI-AAI), Toyama, Japan, 2019: 444–449.
[22]	DENG Liyuan, YANG Ping, and LIU Weidong. An improved genetic algorithm[C]. Proceedings of the 5th International Conference on Computer and Communications (ICCC), Chengdu, China, 2019: 47–51.
[23]	邓兵, 张韫, 李炳荣. 通信对抗原理及应用[M]. 北京: 电子工业出版社, 2017. DENG Bin, ZHANG Yun, and LI Bingrong. Principles and Applications of Communications Countermeasures[M]. Beijing: Publishing House of Electronics Industry, 2017.
[24]	沈阳, 陈永光, 李修和. 基于0-1规划的雷达干扰资源优化分配研究[J]. 兵工学报, 2007, 28(5): 528–532. doi: 10.3321/j.issn:1000-1093.2007.05.005 SHENG Yang, CHENG Yongguang, and LI Xiuhe. Research on optimal distribution of Radar jamming resource based on zero-one programming[J]. Acta Armamentarii, 2007, 28(5): 528–532. doi: 10.3321/j.issn:1000-1093.2007.05.005
[25]	LIU Yan, ECKERT C M, and EARL C. A review of fuzzy AHP methods for decision-making with subjective judgements[J]. Expert Systems with Applications, 2020, 161: 113738. doi: 10.1016/j.eswa.2020.113738

施引文献

期刊类型引用(4)

1.	施一飞. 分布式多维数据流频繁模式挖掘算法设计. 吉林大学学报(信息科学版). 2023(01): 174-179 . 百度学术
2.	郝云权，赵大志，李伟斌，孔满昭，刘森云. POD-BPNN预测模型及结冰条件不确定性量化. 南京航空航天大学学报. 2023(02): 302-310 . 百度学术
3.	杨静，吉晓阳，李少波，胡建军，王阳，刘庭卿. 具有正则化约束的脉冲神经网络机器人触觉物体识别方法. 电子与信息学报. 2023(07): 2595-2604 . 本站查看
4.	姜岚，李远，智李，周蠡，赵阳. 基于POD-RBF代理模型和特征点KNN校正的电力舱温度反演方法. 电子测量技术. 2023(24): 68-76 . 百度学术

其他类型引用(2)

资源附件(0)

访问统计

图(6) / 表(3)

计量

文章访问数: 707
HTML全文浏览量: 290
PDF下载量: 72
被引次数: 6

1. 引言
2. 探地雷达系统建模与ADE-FDTD全波仿真原理
3. 人工神经网络(ANN)替代模型的构建
3.1 ANN替代模型设计
3.2 激活函数的选择与性能比较分析以及抑制过拟合策略
4. 仿真与结果
4.1 模型描述
4.2 ANN替代模型超参数
4.3 基于ANN替代模型的探地雷达系统输出结果不确定性分析
4.4 ANN替代模型的适应性分析与验证
5. 结论

1. 引言
2. 探地雷达系统建模与ADE-FDTD全波仿真原理
3. 人工神经网络(ANN)替代模型的构建
3.1 ANN替代模型设计
3.2 激活函数的选择与性能比较分析以及抑制过拟合策略
4. 仿真与结果
4.1 模型描述
4.2 ANN替代模型超参数
4.3 基于ANN替代模型的探地雷达系统输出结果不确定性分析
4.4 ANN替代模型的适应性分析与验证
5. 结论

参考文献(25)

施引文献

资源附件(0)

访问统计

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

带精英集并行遗传算法的无人机干扰资源调度

doi: 10.11999/JEIT210349

通讯作者:
邓敏　iemdeng@xtu.edu.cn

计量

Unmanned Aerial Vehicle Jamming Resource Scheduling Based on Parallel Genetic Algorithm with Elite Set

1. 引言

2. 探地雷达系统建模与ADE-FDTD全波仿真原理

3. 人工神经网络(ANN)替代模型的构建

3.1 ANN替代模型设计

3.2 激活函数的选择与性能比较分析以及抑制过拟合策略

4. 仿真与结果

4.1 模型描述

4.2 ANN替代模型超参数

4.3 基于ANN替代模型的探地雷达系统输出结果不确定性分析

4.4 ANN替代模型的适应性分析与验证

5. 结论

期刊类型引用(4)

其他类型引用(2)

计量

目录

1. 引言

2. 探地雷达系统建模与ADE-FDTD全波仿真原理

3. 人工神经网络(ANN)替代模型的构建

3.1 ANN替代模型设计

3.2 激活函数的选择与性能比较分析以及抑制过拟合策略

4. 仿真与结果

4.1 模型描述

4.2 ANN替代模型超参数

4.3 基于ANN替代模型的探地雷达系统输出结果不确定性分析

4.4 ANN替代模型的适应性分析与验证

5. 结论

留言板

带精英集并行遗传算法的无人机干扰资源调度

doi: 10.11999/JEIT210349

通讯作者: 邓敏 iemdeng@xtu.edu.cn

计量

出版历程

Unmanned Aerial Vehicle Jamming Resource Scheduling Based on Parallel Genetic Algorithm with Elite Set

1. 引言

2. 探地雷达系统建模与ADE-FDTD全波仿真原理

3. 人工神经网络(ANN)替代模型的构建

3.1 ANN替代模型设计

3.2 激活函数的选择与性能比较分析以及抑制过拟合策略

4. 仿真与结果

4.1 模型描述

4.2 ANN替代模型超参数

4.3 基于ANN替代模型的探地雷达系统输出结果不确定性分析

4.4 ANN替代模型的适应性分析与验证

5. 结论

期刊类型引用(4)

其他类型引用(2)

计量

出版历程

目录

1. 引言

2. 探地雷达系统建模与ADE-FDTD全波仿真原理

3. 人工神经网络(ANN)替代模型的构建

3.1 ANN替代模型设计

3.2 激活函数的选择与性能比较分析以及抑制过拟合策略

4. 仿真与结果

4.1 模型描述

4.2 ANN替代模型超参数

4.3 基于ANN替代模型的探地雷达系统输出结果不确定性分析

4.4 ANN替代模型的适应性分析与验证

5. 结论

通讯作者:
邓敏　iemdeng@xtu.edu.cn