Doppler Frequency Shift Estimation Method for Orthogonal Frequency Division Multiplexing Underwater Acoustic Communication Based on Data Sample Variance
-
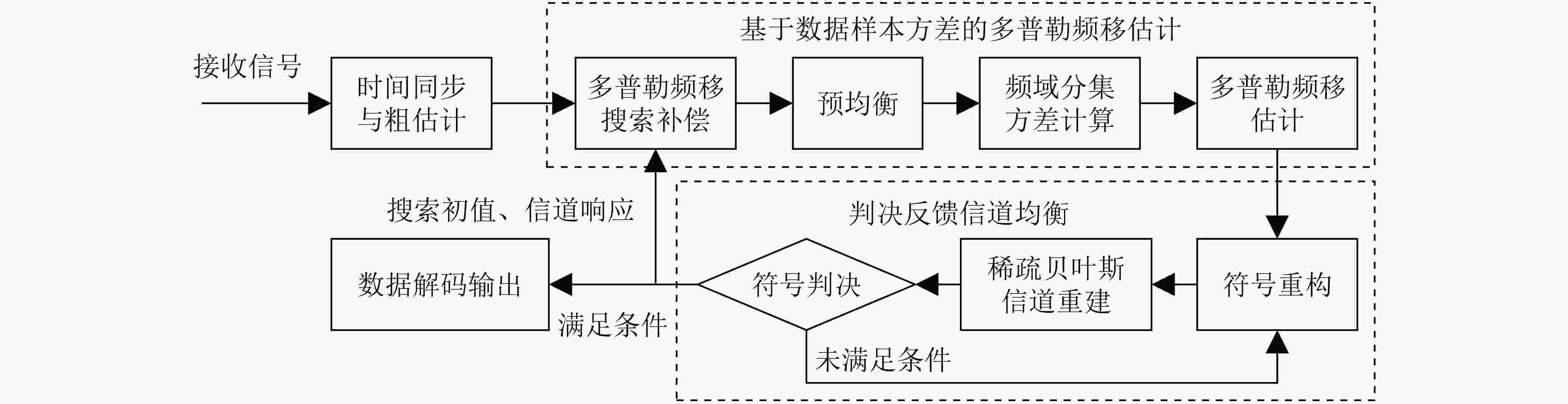
摘要: 针对正交频分复用(OFDM)水声移动通信易受时变多普勒频移影响的缺点,该文提出一种基于数据样本方差的多普勒频移估计方法。利用前序符号的信道估计值恢复当前符号的有效数据序列及其频域分集副本,计算分集副本与数据序列的比值并搜索该比值序列在不同多普勒补偿因子下的方差,选取方差最小时对应的补偿因子作为多普勒频移估计值,利用稀疏贝叶斯学习和判决反馈信道估计算法获得修正后的信道频域响应并传递给后序符号,实现对多普勒频移的实时跟踪。数值仿真验证了该方法的可行性和优越性,海上试验证明,该方法实现了基于无人水下航行器的OFDM水声移动通信,能够对时变多普勒频移进行有效估计。Abstract: To overcome disadvantages of Orthogonal Frequency Division Multiplexing(OFDM) underwater acoustic mobile communication, a data variance-based Doppler frequency shift estimation method is proposed to estimate the time-varying Doppler shifts. The estimated channel response of previous OFDM symbol is utilized to recover the valid data sequence and its frequency-domain diversity. The variance of the ratio of data sequence and diversity copy are calculated under different Doppler compensation factors. Then the correct Doppler frequency shift factor is achieved by seeking the minimum of the variance. Sparse Bayesian learning and decision feedback channel estimation algorithm are used for calculating the revised channel frequency-domain response. The channel response is propagated to the follow-up symbol to track the time-varying Doppler shifts. The feasibility and superiority of the proposed method are verified by simulation. The sea trail demonstrates that the proposed algorithm can effectively estimate the Doppler shifts in underwater acoustic OFDM mobile communication for Unmanned Underwater Vehicle.
-
表 1 不同多普勒频移估计算法所需计算量
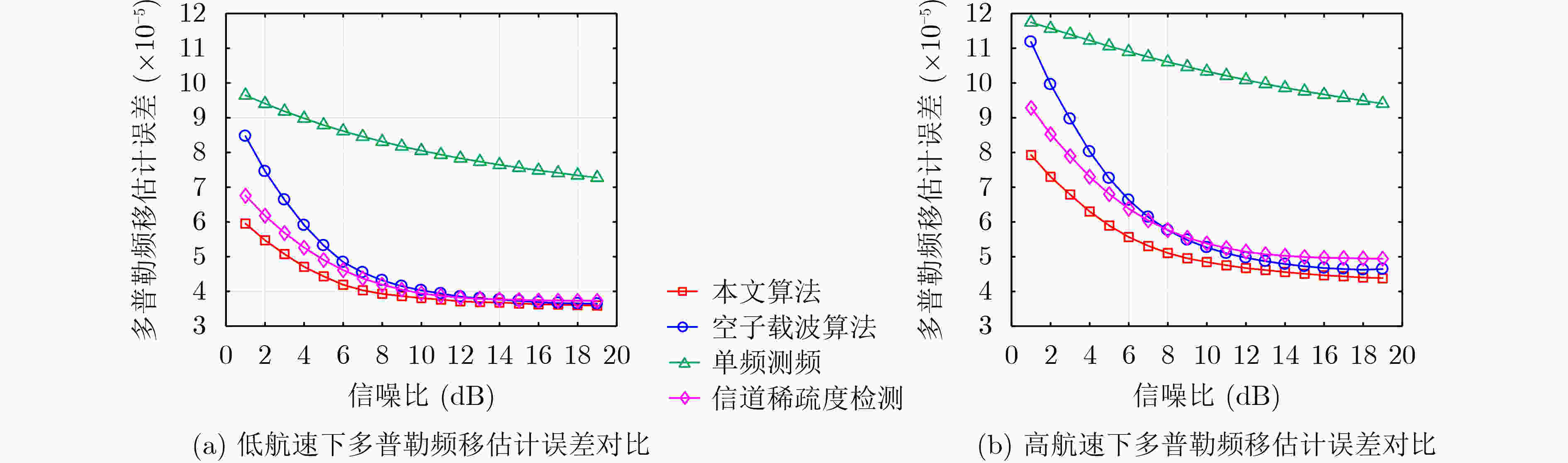
多普勒频移估计算法 复数乘法 复数加法 单频测频 2.46×105 4.92×105 空子载波 4.20×107 4.20×107 信道稀疏度检测 1.05×107 2.10×107 本文算法 4.92×106 9.84×106 表 2 OFDM系统仿真参数
参数 数值 参数 数值 采样率(kHz) 192 OFDM符号周期(ms) 170.7 通信频段(B/kHz) 4~8 循环前缀长度(ms) 43 有效子载波数 681 数据映射方式 QPSK 表 3 低航速下不同多普勒频移估计方法的误码率统计结果
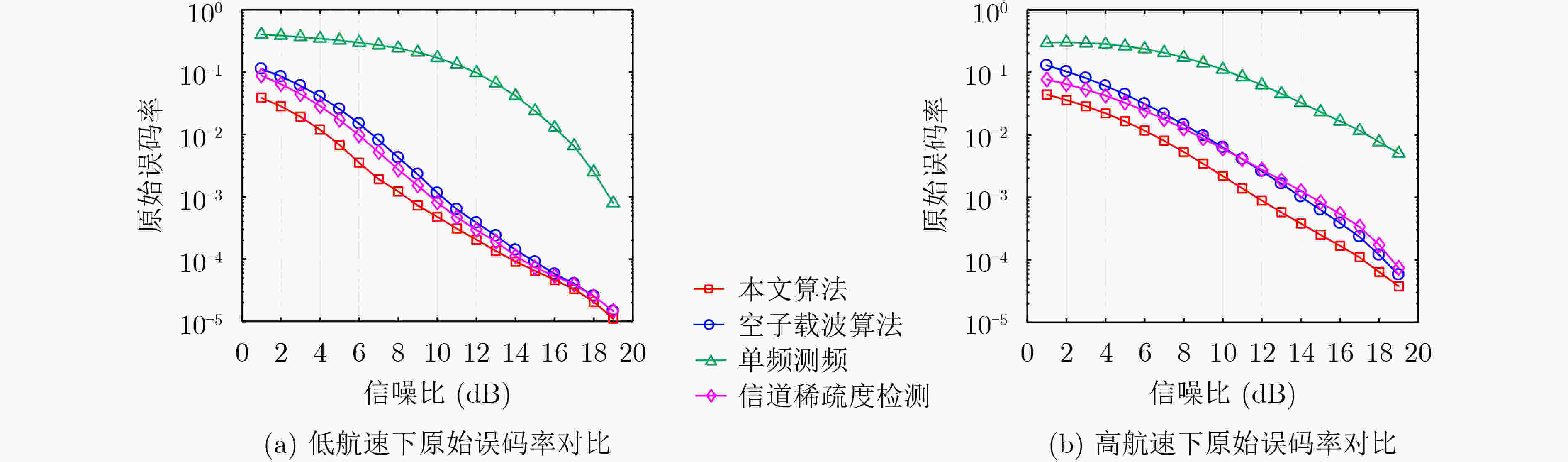
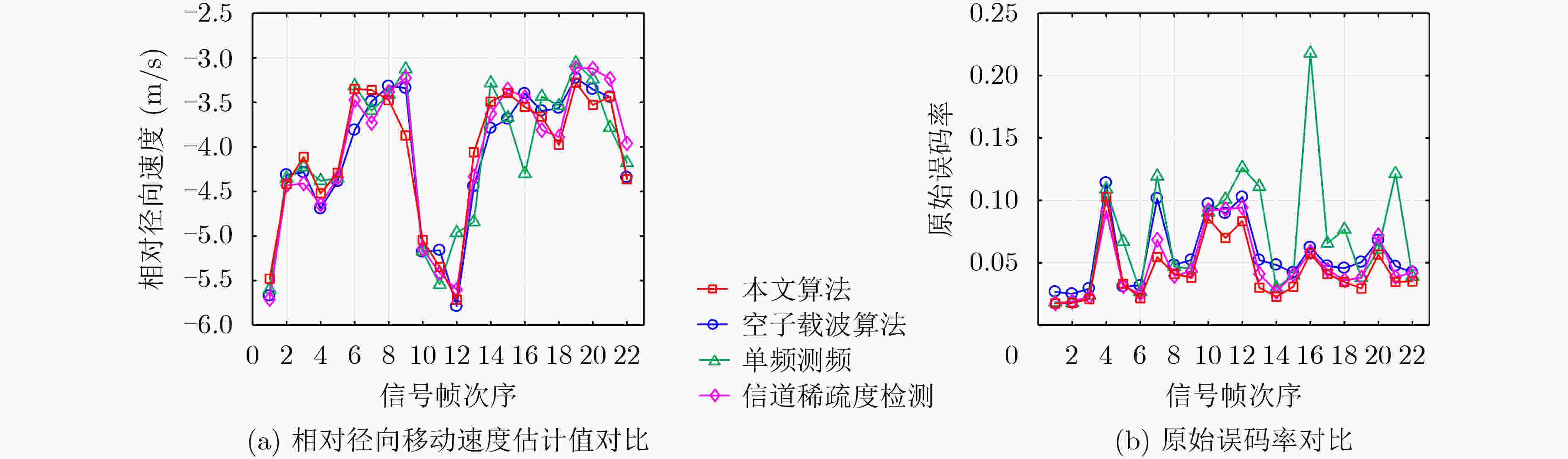
多普勒频移估计算法 原始误码率 解码后误码率 本文算法 0.0200 7.960×10–5 空子载波算法 0.0390 4.117×10–4 单频测频 0.0704 4.401×10–3 信道稀疏度检测 0.0305 9.157×10–4 表 4 高航速下不同多普勒频移估计方法的误码率统计结果
多普勒频移估计算法 原始误码率 解码后误码率 本文算法 0.0435 6.340×10–4 空子载波算法 0.0862 4.795×10–3 单频测频 0.1174 7.351×10–3 信道稀疏度检测 0.0639 2.180×10–3 -
[1] 赵世铎, 鄢社锋. 基于扩展路径识别算法的水声OFDM系统低复杂度迭代稀疏信道估计[J]. 电子与信息学报, 2021, 43(3): 752–757. doi: 10.11999/JEIT200582ZHAO Shiduo and YAN Shefeng. Low-complexity iterative sparse channel estimation for underwater acoustic OFDM systems based on generalized path identification algorithm[J]. Journal of Electronics &Information Technology, 2021, 43(3): 752–757. doi: 10.11999/JEIT200582 [2] 强夕竹, 乔钢, 周锋. 一种改进的水声正交频分复用稀疏信道时延估计算法[J]. 电子与信息学报, 2021, 43(3): 817–825. doi: 10.11999/JEIT200660QIANG Xizhu, QIAO Gang, and ZHOU Feng. An improved delay estimation algorithm for underwater acoustic OFDM sparse channel[J]. Journal of Electronics &Information Technology, 2021, 43(3): 817–825. doi: 10.11999/JEIT200660 [3] MA Lu, ZHOU Shengli, QIAO Gang, et al. Superposition coding for downlink underwater acoustic OFDM[J]. IEEE Journal of Oceanic Engineering, 2017, 42(1): 175–187. [4] 支绍龙, 袁兆凯, 李宇, 等. 一种小型化水声信号调制发射系统[J]. 仪器仪表学报, 2012, 33(7): 1668–1675. doi: 10.3969/j.issn.0254-3087.2012.07.033ZHI Shaolong, YUAN Zhaokai, LI Yu, et al. Miniaturized underwater acoustic signal modulation and transmission system[J]. Chinese Journal of Scientific Instrument, 2012, 33(7): 1668–1675. doi: 10.3969/j.issn.0254-3087.2012.07.033 [5] WAN Lei, WANG Zhaohui, ZHOU Shengli, et al. Performance comparison of Doppler scale estimation methods for underwater acoustic OFDM[J]. Journal of Electrical and Computer Engineering, 2012, 2012: 703243. [6] SUN Haixin, XU Xiaoka, MA Li, et al. Carrier frequency offset and impulse noise estimation for underwater acoustic orthogonal frequency division multiplexing[J]. Chinese Journal of Acoustics, 2014, 33(3): 289–298. [7] 袁兆凯, 隋天宇, 李宇, 等. 水声扩频通信中多普勒估计与补偿算法研究[J]. 电子与信息学报, 2012, 34(1): 51–56.YUAN Zhaokai, SUI Tianyu, LI Yu, et al. The estimation and compensation of Doppler effect on underwater acoustic spread spectrum communication[J]. Journal of Electronics &Information Technology, 2012, 34(1): 51–56. [8] 王彪, 支志福, 戴跃伟. 移动水声通信多径传输非一致多普勒估计方法研究[J]. 电子与信息学报, 2015, 37(3): 733–738. doi: 10.11999/JEIT140665WANG Biao, ZHI Zhifu, and DAI Yuewei. Study on non-uniform Doppler estimation for underwater acoustic mobile communications with multipath transmission[J]. Journal of Electronics &Information Technology, 2015, 37(3): 733–738. doi: 10.11999/JEIT140665 [9] SHARIF B S, NEASHAM J, HINTON O R, et al. A computationally efficient Doppler compensation system for underwater acoustic communications[J]. IEEE Journal of Oceanic Engineering, 2000, 25(1): 52–61. doi: 10.1109/48.820736 [10] LI Baosheng, ZHOU Shengli, STOJANOVIC M, et al. Multicarrier communication over underwater acoustic channels with nonuniform Doppler shifts[J]. IEEE Journal of Oceanic Engineering, 2008, 33(2): 198–209. doi: 10.1109/JOE.2008.920471 [11] 普湛清, 王巍, 张扬帆, 等. UUV平台OFDM水声通信时变多普勒跟踪与补偿算法[J]. 仪器仪表学报, 2017, 38(7): 1634–1644. doi: 10.3969/j.issn.0254-3087.2017.07.009PU Zhanqing, WANG Wei, ZHANG Yangfan, et al. Time-variant Doppler tracking and compensation in underwater acoustic OFDM communication for UUV platform[J]. Chinese Journal of Scientific Instrument, 2017, 38(7): 1634–1644. doi: 10.3969/j.issn.0254-3087.2017.07.009 [12] MASON S F, BERGER C R, ZHOU Shengli, et al. Detection, synchronization, and Doppler scale estimation with multicarrier waveforms in underwater acoustic communication[J]. IEEE Journal on Selected Areas in Communications, 2008, 26(9): 1638–1649. doi: 10.1109/JSAC.2008.081204 [13] MA Lu, QIAO Gang, and LIU Songzuo. A combined Doppler scale estimation scheme for underwater acoustic OFDM system[J]. Journal of Computational Acoustics, 2015, 23(4): 1540004. doi: 10.1142/S0218396X15400044 [14] LE K N and DABKE K P. BER of OFDM with diversity and pulse shaping in Rayleigh fading environments[J]. Digital Signal Processing, 2010, 20(6): 1687–1696. doi: 10.1016/j.dsp.2010.03.015 [15] BYUN S H, SEONG W, and KIM S M. Sparse underwater acoustic channel parameter estimation using a wideband receiver array[J]. IEEE Journal of Oceanic Engineering, 2013, 38(4): 718–729. doi: 10.1109/JOE.2013.2258222 [16] 乔钢, 王巍, 刘凇佐, 等. 改进的多输入多输出正交频分复用水声通信判决反馈信道估计算法[J]. 声学学报, 2016, 41(1): 94–104.QIAO Gang, WANG Wei, LIU Songzuo, et al. An improved decision feedback channel estimation algorithm for multiple-input multiple-output orthogonal frequency division multiplexing underwater acoustic communication[J]. Acta Acustica, 2016, 41(1): 94–104. [17] 王巍, 普湛清, 张扬帆, 等. 稀疏信道条件下正交多载波扩频水声通信无导频信道估计算法[J]. 声学学报, 2019, 44(4): 657–664.WANG Wei, PU Zhanqing, ZHANG Yangfan, et al. A pilot-free channel estimation algorithm for orthogonal multicarrier spread spectrum communication via sparse underwater acoustic channel[J]. Acta Acustica, 2019, 44(4): 657–664. [18] CANDÈS E J, WAKIN M B, and BOYD S P. Enhancing sparsity by reweighted ℓ1 minimization[J]. Journal of Fourier Analysis and Applications, 2008, 14(5): 877–905. [19] EDFORS O, SANDELL M, VAN DE BEEK J J, et al. OFDM channel estimation by singular value decomposition[C]. Vehicular Technology Conference-VTC, Atlanta, USA, 1996: 923–927. [20] WIPF D P and RAO B D. Sparse Bayesian learning for basis selection[J]. IEEE Transactions on Signal Processing, 2004, 52(8): 2153–2164. doi: 10.1109/TSP.2004.831016 [21] WIPF D P and RAO B D. An empirical Bayesian strategy for solving the simultaneous sparse approximation problem[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3704–3716. doi: 10.1109/TSP.2007.894265 [22] 陈平, 郭秋歌, 李攀, 等. OFDM系统中基于贝叶斯学习的联合稀疏信道估计与数据检测[J]. 计算机科学, 2020, 47(S2): 349–353.CHEN Ping, GUO Qiuge, LI Pan, et al. Joint sparse channel estimation and data detection based on Bayesian learning in OFDM system[J]. Computer Science, 2020, 47(S2): 349–353. [23] VITERBI A J. An intuitive justification and a simplified implementation of the MAP decoder for convolutional codes[J]. IEEE Journal on Selected Areas in Communications, 1998, 16(2): 260–264. doi: 10.1109/49.661114 -





 下载:
下载:

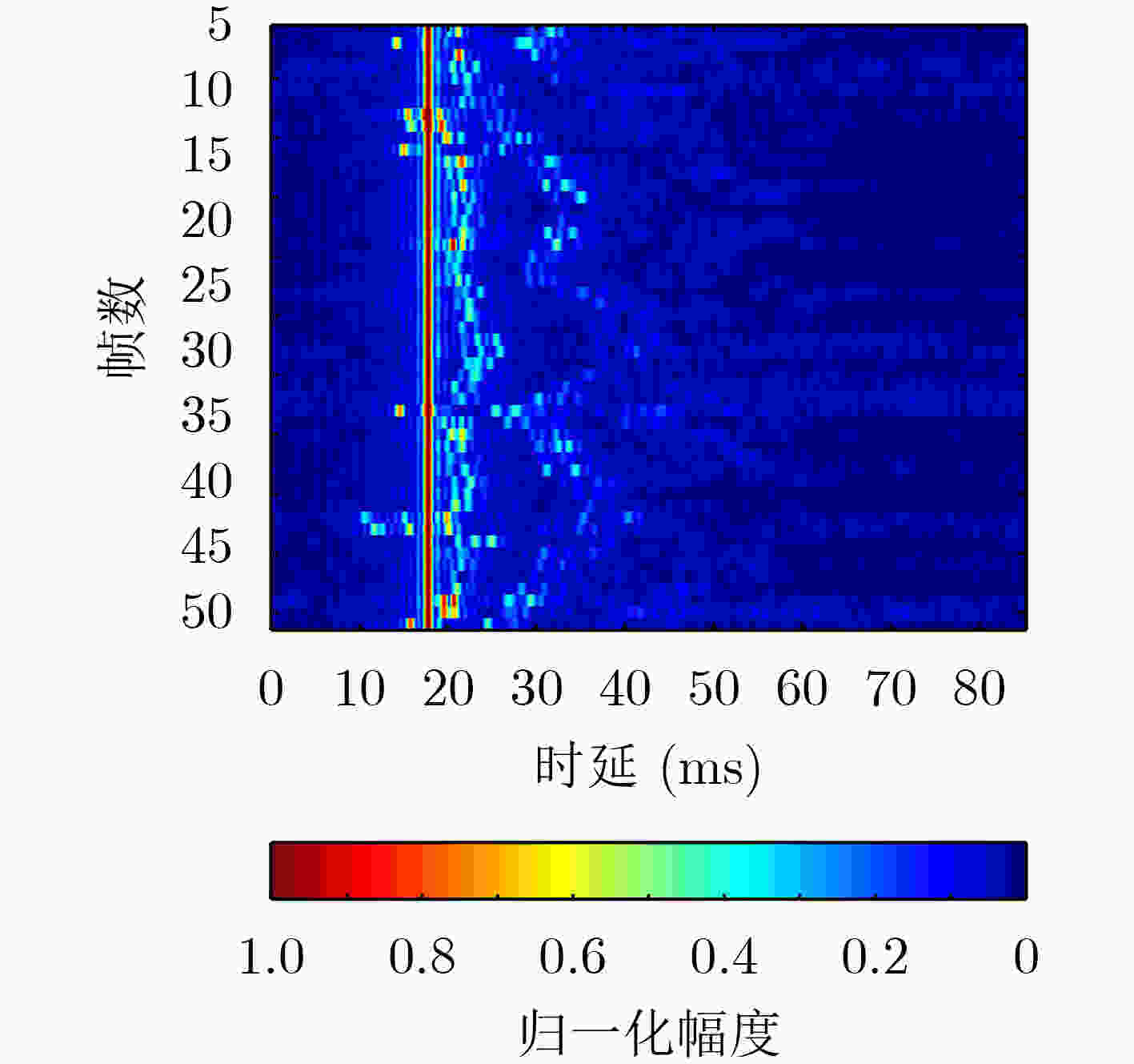
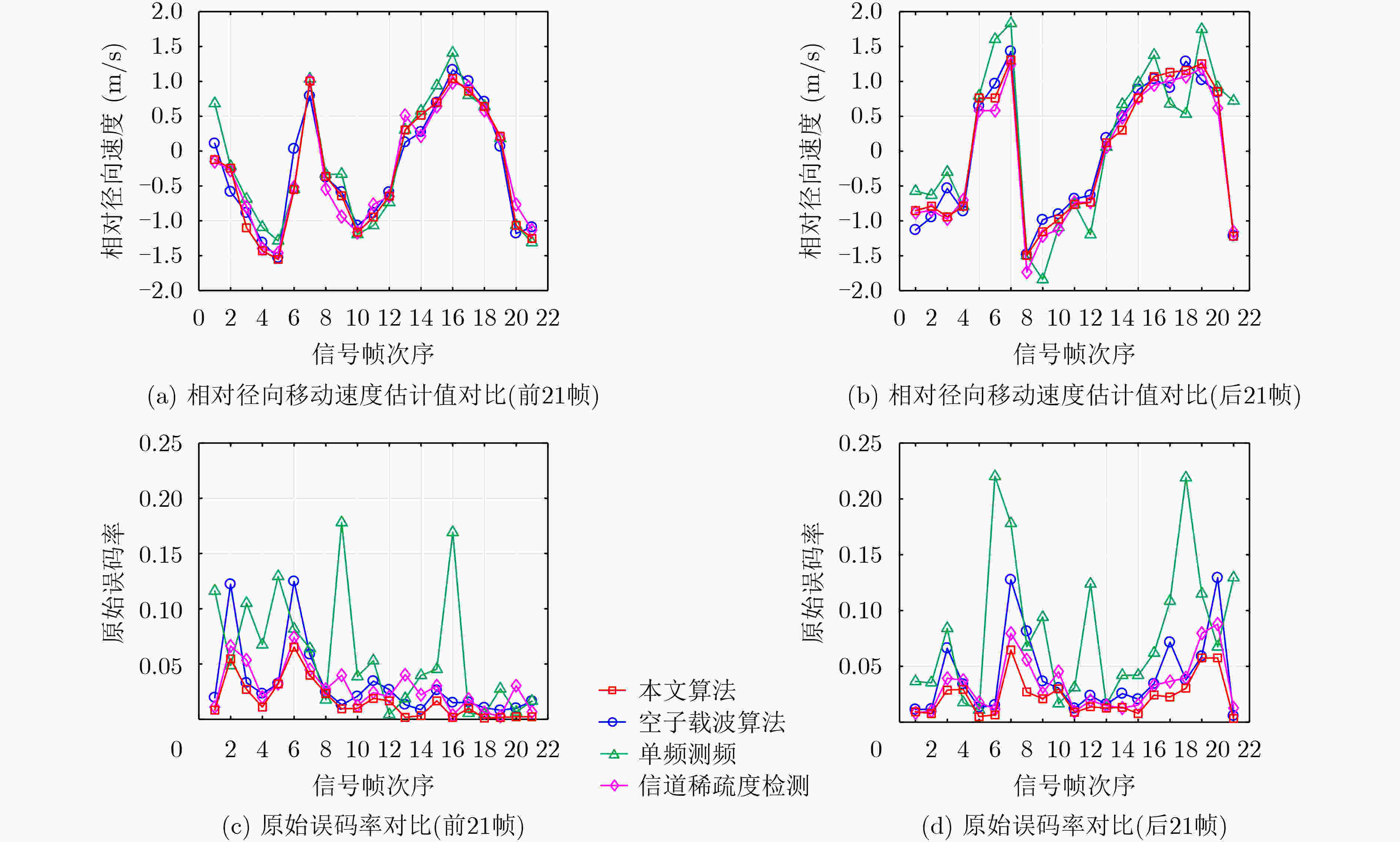
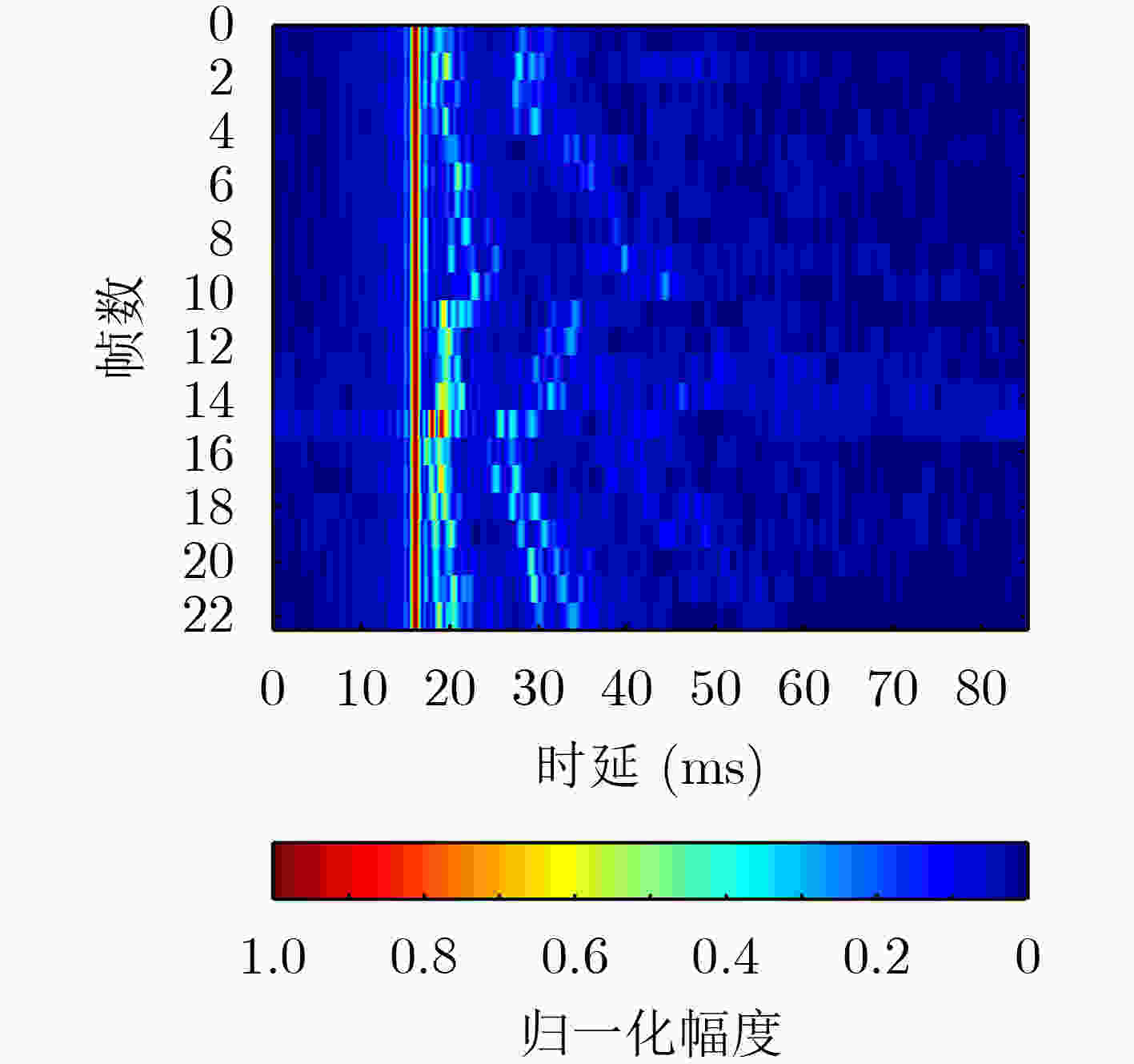


 下载:
下载:
