Channel Adaptive Ultrasound Image Denoising Method Based on Residual Encoder-decoder Networks
-
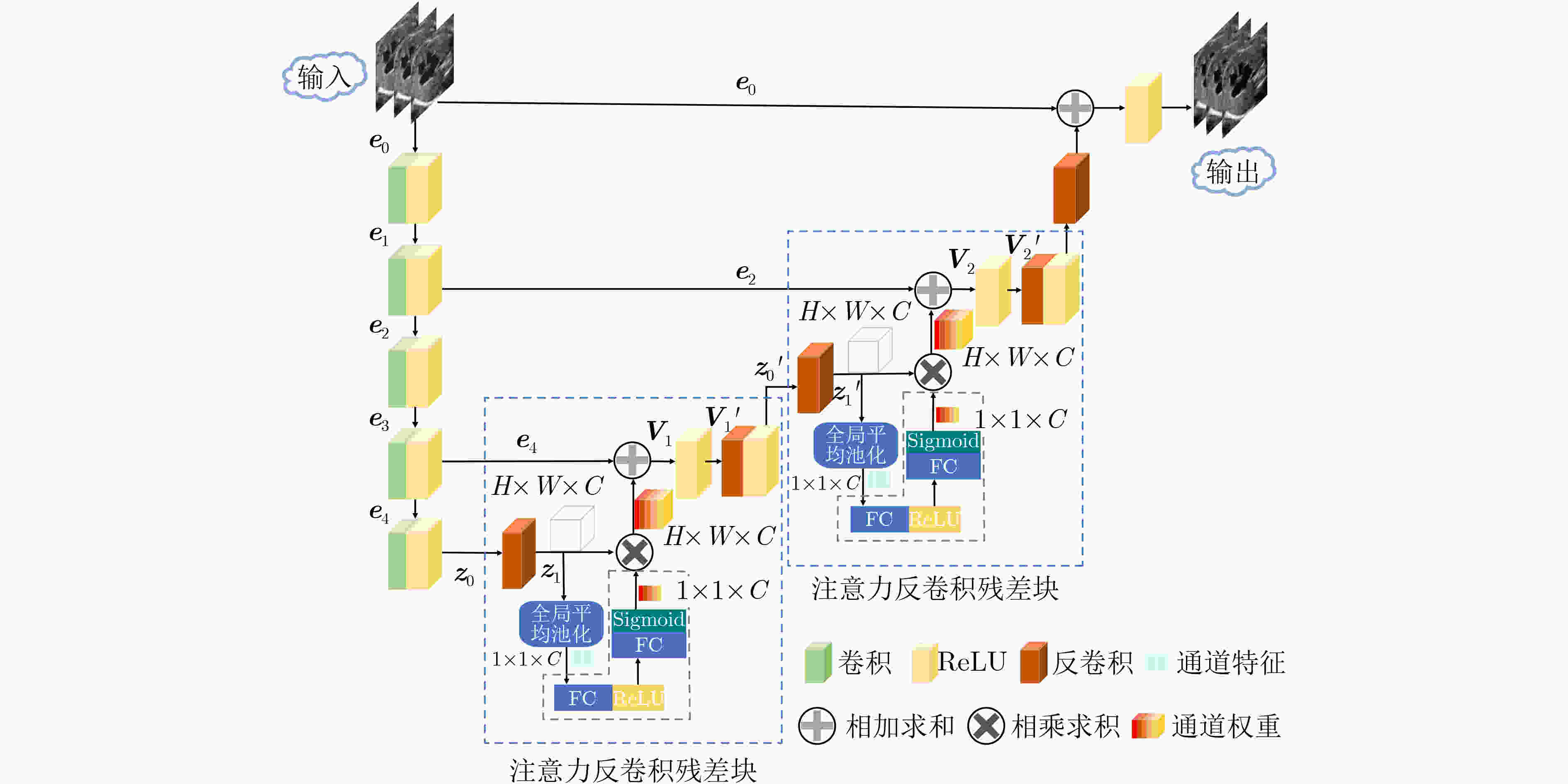
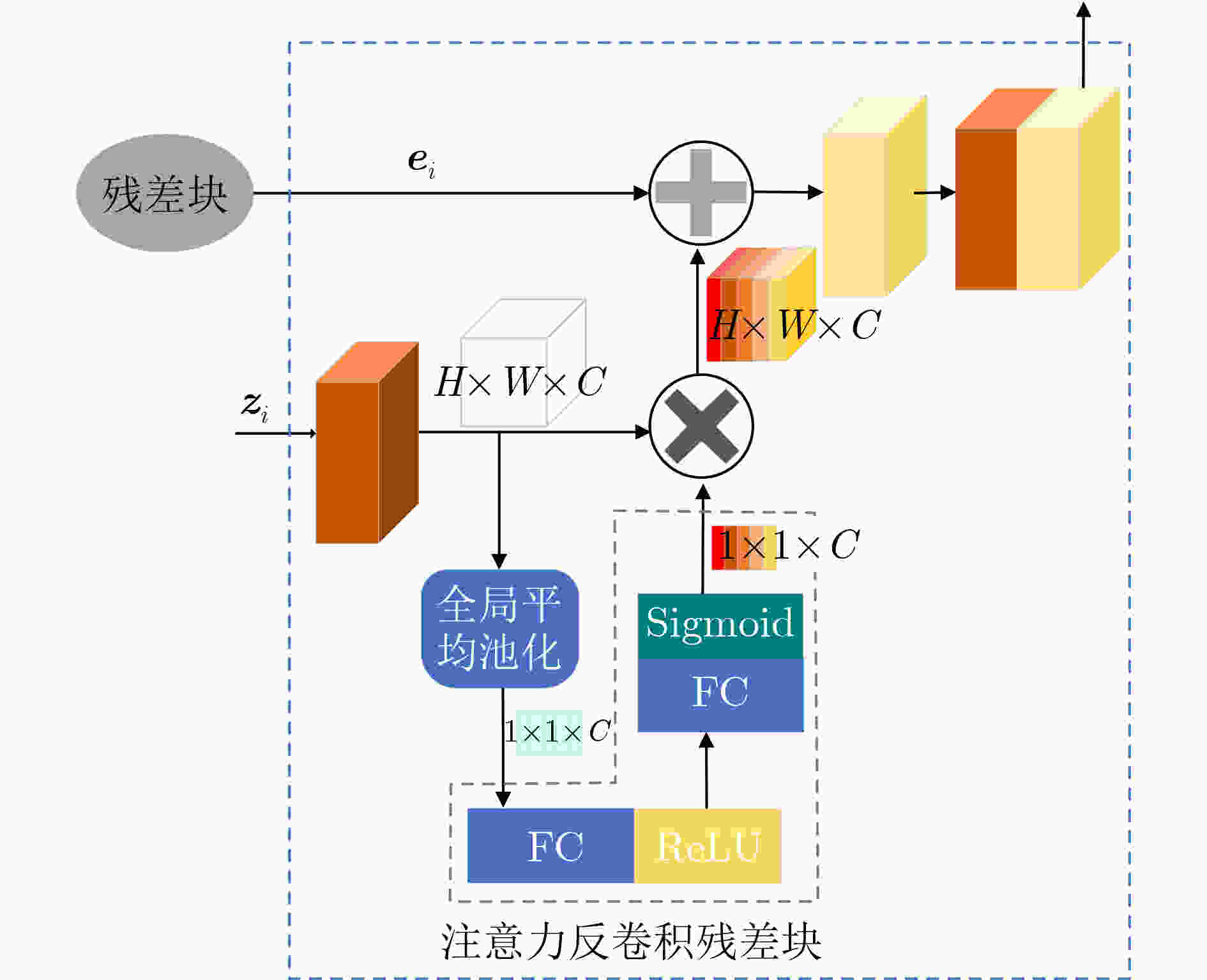
摘要: 超声图像去噪对提高超声图像的视觉质量和完成其他相关的计算机视觉任务都至关重要。超声图像中的特征信息与斑点噪声信号较为相似,用已有的去噪方法对超声图像去噪,容易造成超声图像纹理特征丢失,这会对临床诊断的准确性产生严重的干扰。因此,在去除斑点噪声的过程中,需尽量保留图像的边缘纹理信息才能更好地完成超声图像去噪任务。该文提出一种基于残差编解码器的通道自适应去噪模型(RED-SENet),能有效去除超声图像中的斑点噪声。在去噪模型的解码器部分引入注意力反卷积残差块,使本模型可以学习并利用全局信息,从而选择性地强调关键通道的内容特征,抑制无用特征,能提高模型去噪的性能。在2个私有数据集和2个公开数据集上对该模型进行定性评估和定量分析,与一些先进的方法相比,该模型的去噪性能有显著提升,并在噪声抑制以及结构保持方面具有良好的效果。Abstract: The denoising of ultrasound images is very important to improve the visual quality of ultrasound images and to accomplish other related computer vision tasks. The feature information in ultrasound images is similar to the speckle noise signal. The existing denoising methods for ultrasound images denoising are easy to cause the loss of texture features of ultrasound images, which will cause serious interference to the accuracy of clinical diagnosis. Therefore, in the process of speckle noise removal, the edge texture information of images should be retained as far as possible to complete better the task of ultrasound images denoising. RED-SENet (Residual Encoder-Decoder with Squeeze-and-Excitation Network), a channel adaptive denoising model based on residual encoder-decoder is presented, which can effectively remove speckle noise in ultrasound images. By introducing the attention deconvolution residual block in the decoder part of the denoising model, the model can learn and use the global information, selective emphasizing the content features of the key channels and suppress the useless features, which can improve the denoising performance of the model. The model is qualitatively evaluated and quantitatively analyzed on 2 private datasets and 2 public datasets, respectively. Compared with some advanced methods, the denoising performance of the model is significantly improved, and it has advantages in noise suppression and structure preservation.
-
表 1 RED-SENet超声图像去噪模型训练算法
输入:训练集${\boldsymbol{S}} = \left\{ {\left( { { {\boldsymbol{X} }_{\text{1} } },{ {\boldsymbol{Y} }_1} } \right),\left( { { {\boldsymbol{X} }_{\text{2} } },{ {\boldsymbol{Y} }_{\text{2} } } } \right), \cdots ,\left( { { {\boldsymbol{X} }_N},{ {\boldsymbol{Y} }_N} } \right)} \right\}$;
$\left( { {{\boldsymbol{X}}_i}{\text{,} }{{\boldsymbol{Y}}_i} } \right)$为带噪声图像和干净图像的图像对输出:RED-SENet去噪模型$ {\varphi _{\text{d}}} $; 初始化:学习率${\rm{lr}}$;训练次数$ T $;批次大小$ M $; 过程: (1) while $ t \lt T $do: (2) 随机打乱训练集${\boldsymbol{S}} = \left\{ {\left( { {{\boldsymbol{X}}_{\text{1} } },{{\boldsymbol{Y}}_1} } \right),\left( { {{\boldsymbol{X}}_{\text{2} } },{{\boldsymbol{Y}}_{\text{2} } } } \right), \cdots ,\left( { {{\boldsymbol{X}}_N},{{\boldsymbol{Y}}_N} } \right)} \right\}$
中的超声图像(3) $\left( { {{\boldsymbol{X}}_i}{\text{,} }{{\boldsymbol{Y}}_i} } \right) \leftarrow {f_{ {\text{data} } } }\left( {\boldsymbol{S}} \right)$//{从超声图像训练集$ S $中随机选择超
声图像对}
(4) for $ k \in \left( {1,2, \cdots ,\dfrac{N}{M}} \right) $ do:(5) ${{\boldsymbol{X}}^k} = \left\{ {{\boldsymbol{X}}_i^k} \right\}_{i = \left( {k - 1} \right)M + 1}^{kM}$,${{\boldsymbol{Y}}^k} = \left\{ {{\boldsymbol{Y}}_i^k} \right\}_{i = \left( {k - 1} \right)M + 1}^{kM}$
//{第$ k $批带噪声的图像${{\boldsymbol{X}}^k}$,第$ k $批干净图像${{\boldsymbol{Y}}^k}$,第$ k $批
中的第$ i $张带噪声的图像${\boldsymbol{X}}_i^k$,第$ k $批中的第$ i $张干净的图
像${\boldsymbol{Y}}_i^k$}(6) ${{\boldsymbol{P}}^k} \leftarrow {\varphi _d}\left( { {{\boldsymbol{X}}^k} } \right)$//{第$ k $批图像对中的带噪声的图像${{\boldsymbol{X}}^k}$
输入到去噪模型$ {\varphi _d} $处理,得到第$ k $批预测图像
${{\boldsymbol{P}}^k} = \left\{ {{\boldsymbol{P}}_i^k} \right\}_{i = \left( {k - 1} \right)M + 1}^{kM}$}(7) ${L_{ \rm{M} } } \leftarrow \dfrac{1}{ {2M} }\sum\limits_{i = 1}^M { { {\left\| { {\boldsymbol{Y} }_i^k - {\boldsymbol{P} }_i^k} \right\|}^2} }$//{计算第$ k $批经过去噪模
型训练损失}(8) $\dfrac{ {\partial {L_{\rm{M} } } } }{ {\partial {\theta _{\rm{d} } } } } \leftarrow {\nabla _{ {\theta _{\rm{d} } } } }{L_{\rm{M}}}$//{计算关于去噪模型$ {\varphi _{\text{d}}} $训练参数${\theta _{\rm{d}}}$的
梯度}(9) ${\theta _{\rm{d}}} \leftarrow {\theta _{\rm{d}}} - {\rm{lr} } \cdot { {\partial {L_{\rm{M}}} } \mathord{\left/ {\vphantom { {\partial {L_M} } {\partial {\theta _d} } } } \right. } {\partial {\theta _{\rm{d}}} } }$//{更新去噪模型${\varphi _{\rm{d}}}$的参数${\theta _{\rm{d}}}$} (10) end for (11) end while (12) 保存训练完成的去噪模型$ {\varphi _d} $ 表 2 RED-SENet去噪网络结构与参数配置
类型 配置 Conv1 卷积核大小:$ 96 \times 5 \times 5 $,步长:1,填充:0,ReLU Conv2 卷积核大小:$ 96 \times 5 \times 5 $,步长:1,填充:0,ReLU Conv3 卷积核大小:$ 96 \times 5 \times 5 $,步长:1,填充:0,ReLU Conv4 卷积核大小:$ 96 \times 5 \times 5 $,步长:1,填充:0,ReLU Conv5 卷积核大小:$ 96 \times 5 \times 5 $,步长:1,填充:0,ReLU ADR块1 卷积核大小:$ 96 \times 5 \times 5 $,步长:1,填充:0
池化层1:全局平均池化
全连接层1:输入:96,输出:6
全连接层2:输入:6,输出:96,Sigmoid
元素逐位相乘进行扩展
ReLU,卷积核大小:$ 96 \times 5 \times 5 $,步长:1,填充:0,ReLUADR块2 卷积核大小:$ 96 \times 5 \times 5 $,步长:1,填充:0
池化层2:全局平均池化
全连接层3:输入:96,输出:6
全连接层4:输入:6,输出:96,Sigmoid
元素逐位相乘进行扩展
ReLU,卷积核大小:$ 96 \times 5 \times 5 $,步长:1,填充:0,ReLUDeconv1 卷积核大小:$ 96 \times 5 \times 5 $,步长:1,填充:0 表 3 胎儿心脏超声数据集在不同噪声情况下的实验对比
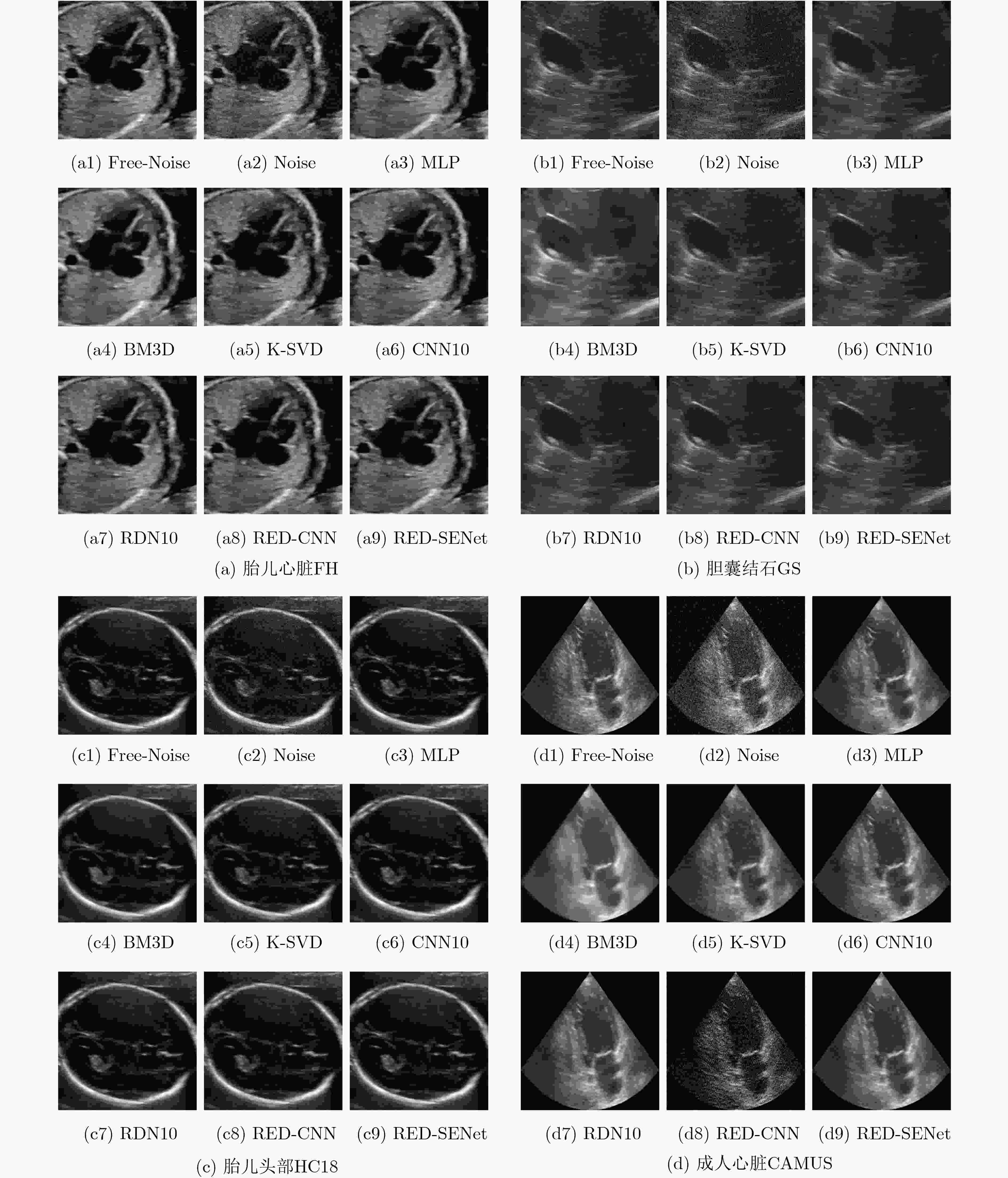
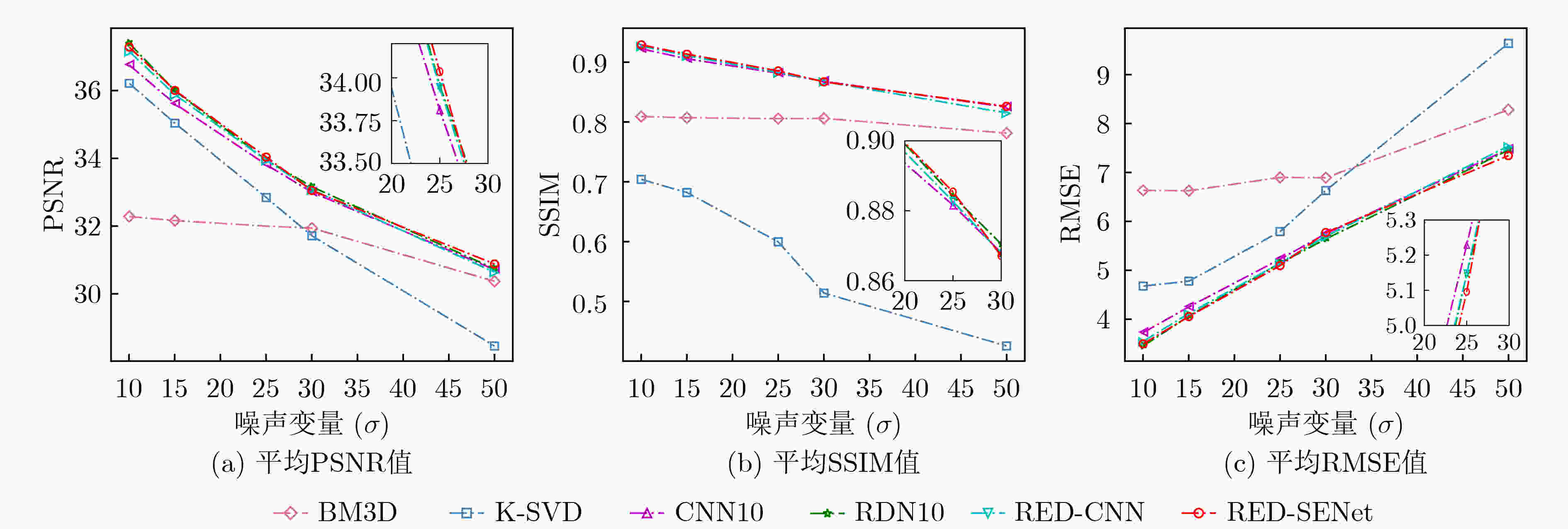
方法 噪声变量$ \sigma $ 10 15 25 30 PSNR SSIM RMSE PSNR SSIM RMSE PSNR SSIM RMSE PSNR SSIM RMSE MLP[18] 37.0250 0.9208 3.9435 33.0038 0.8425 6.1543 33.6847 0.8740 5.2637 31.2649 0.7862 7.1016 BM3D[19] 32.2814 0.8092 6.6343 32.1621 0.8071 6.6271 31.9999 0.8057 6.8974 31.9389 0.8061 6.8914 K-SVD[20] 36.2125 0.7041 4.6770 35.0379 0.6820 4.7779 32.8427 0.5996 5.7918 31.7136 0.5140 6.6300 CNN10[21] 36.7547 0.9224 3.7259 35.6082 0.9057 4.2510 33.8123 0.8816 5.2287 33.0003 0.8680 5.7462 RDN10[22] 37.3945 0.9315 3.4531 35.9948 0.9140 4.0620 33.9530 0.8842 5.1464 33.1601 0.8705 5.6412 RED-CNN[10] 37.1554 0.9270 3.5472 35.8805 0.9109 4.1167 33.9443 0.8827 5.1485 33.0720 0.8677 5.6960 本文RED-SENet 37.2824 0.9290 3.4960 36.0049 0.9135 4.0540 34.0361 0.8854 5.0957 33.0493 0.8671 5.7712 原始图像 28.0914 0.6192 10.0497 24.9016 0.4519 14.5086 20.7652 0.2594 23.3596 19.2920 0.2051 27.6783 表 4 胆囊结石超声数据集在不同噪声情况下的实验对比
方法 噪声变量$ \sigma $ 10 15 25 30 PSNR SSIM RMSE PSNR SSIM RMSE PSNR SSIM RMSE PSNR SSIM RMSE MLP[18] 36.3828 0.9081 4.01526 34.4231 0.8567 5.7431 32.7020 0.8243 6.2067 30.9754 0.7986 6.0047 BM3D[19] 36.5529 0.9108 3.8123 34.7211 0.8749 5.4593 32.6278 0.8224 5.8419 31.2606 0.8093 6.1137 K-SVD[20] 35.2304 0.5846 4.4622 33.6199 0.5208 5.3631 31.5914 0.4078 6.7474 30.6680 0.3783 7.4955 CNN10[21] 36.5396 0.9169 3.8205 34.7340 0.8833 4.7085 32.635 0.8343 6.0030 31.9594 0.8163 6.4927 RDN10[22] 36.3706 0.9155 3.898 34.4965 0.8801 4.8414 32.4087 0.8268 6.1628 31.2559 0.8048 7.0266 RED-CNN[10] 35.7836 0.9042 4.1613 33.9175 0.8646 5.1630 31.7466 0.8053 6.6363 31.1536 0.7791 7.1057 本文RED-SENet 36.6488 0.9203 3.7712 34.7828 0.8848 4.6817 32.7704 0.8368 5.9116 31.9853 0.8185 6.4720 原始图像 28.0615 0.5771 10.0848 24.755 0.4127 14.7581 20.5992 0.2353 23.8186 19.1407 0.1868 28.1763 表 5 胎儿头部超声数据集在不同噪声情况下的实验对比
方法 噪声变量$ \sigma $ 10 15 25 30 PSNR SSIM RMSE PSNR SSIM RMSE PSNR SSIM RMSE PSNR SSIM RMSE MLP[18] 39.4777 0.9562 3.0018 36.4658 0.9033 3.9986 35.1046 0.9112 4.6981 33.7753 0.8544 6.2157 BM3D[19] 36.8696 0.9287 4.0438 36.8041 0.9262 4.0323 35.1324 0.9121 4.6795 34.0274 0.8802 6.4565 K-SVD[20] 39.0871 0.7306 2.8706 36.4840 0.9259 3.8646 34.2191 0.8896 4.8119 32.3865 0.4321 6.1468 CNN10[21] 39.5865 0.956 2.7229 36.9170 0.9342 3.7053 34.7147 0.9074 4.7567 32.9189 0.8658 5.8005 RDN10[22] 39.9455 0.9606 2.6035 37.7666 0.9421 3.3447 35.0829 0.9096 4.5505 34.1220 0.8960 5.0764 RED-CNN[10] 36.5529 0.9188 3.8123 34.7045 0.8826 4.7225 32.7723 0.8368 5.9098 31.9544 0.8136 6.4951 本文RED-SENet 39.9177 0.9614 2.6097 37.6201 0.9412 3.3990 35.1370 0.9123 4.5182 34.2254 0.8978 5.0211 原始图像 28.5245 0.5621 9.5626 25.2038 0.399 14.0193 21.1366 0.2297 22.3967 19.7165 0.1836 26.3751 表 6 CAMUS头部超声数据集在不同噪声情况下的实验对比
方法 噪声变量$ \sigma $ 10 15 25 30 PSNR SSIM RMSE PSNR SSIM RMSE PSNR SSIM RMSE PSNR SSIM RMSE MLP[18] 35.7896 0.9158 3.9976 31.7483 0.8305 7.1075 31.7362 0.8100 6.4872 29.4522 0.7907 8.7962 BM3D[19] 32.0905 0.8624 6.3538 31.0343 0.8256 7.1731 29.8946 0.7925 8.1778 29.5096 0.8011 8.5485 K-SVD[20] 33.4149 0.3969 5.4508 32.3028 0.3839 6.1989 30.8348 0.3405 5.9092 30.6680 0.3783 7.4955 CNN10[21] 36.0644 0.9402 4.0146 34.1212 0.9087 5.0213 32.0312 0.8630 6.3881 31.3639 0.8436 6.8986 RDN10[22] 36.3061 0.9430 3.9044 34.2546 0.9115 4.9451 30.2393 0.6911 7.8501 31.4248 0.8407 6.8504 RED-CNN[10] 36.0761 0.9406 4.0092 34.1174 0.9087 5.0237 32.0123 0.8625 6.4021 31.0123 0.8225 6.4021 RED-SENet(本文方法) 36.1652 0.9416 3.9680 34.2439 0.9107 4.9510 32.0942 0.8623 6.3422 31.4028 0.8458 6.8680 原始图像 28.0615 0.5771 10.0848 24.755 0.4127 14.7581 20.5992 0.2353 23.8186 19.1407 0.1868 28.1763 表 7 不同方法在4个数据集上的定量结果分析(
$ \sigma = 50 $ )方法 FH GS HC18 CAMUS PSNR SSIM RMSE PSNR SSIM RMSE PSNR SSIM RMSE PSNR SSIM RMSE MLP[18] 30.4846
±1.020.8071
±0.01267.8512
±0.001529.9573
±1.300.7534
±0.00658.4215
±0.001331.7773
±1.480.8523
±0.00857.1479
±0.001429.1950
±1.250.6216
±0.011610.1547
±0.0019BM3D[19] 30.3689
±1.610.7814
±0.01278.2808
±0.001229.8486
±1.170.6962
±0.01448.1261
±0.001630.0354
±1.130.7731
±0.00726.9196
±0.000928.2329
±1.060.7253
±0.00759.9010
±0.0016K-SVD[20] 28.4602
±1.430.4255
±0.01689.6388
±0.001827.8136
±1.330.2403
±0.009610.391
±0.001230.7154
±1.440.8076
±0.00787.3864
±0.000827.5461
±1.740.2438
±0.006710.7001
±0.0011CNN10[21] 30.7148
±1.160.8249
±0.01297.4758
±0.001130.0116
±1.580.7641
±0.00828.1224
±0.001031.4681
±1.230.8526
±0.00896.8891
±0.001029.6280
±1.600.7987
±0.00648.4264
±0.0009RDN10[22] 30.7415
±1.320.8223
±0.00747.4541
±0.001329.6762
±1.490.7439
±0.00878.4430
±0.000731.4794
±1.460.8451
±0.01216.8725
±0.000929.6327
±1.630.7976
±0.00668.4254
±0.0015RED-CNN[10] 30.6400
±1.350.8152
±0.00867.5361
±0.000928.3693
±1.550.6696
±0.00799.7852
±0.000830.0165
±1.520.7598
±0.01028.1241
±0.000729.7174
±1.570.7996
±0.00828.3412
±0.0008RED-SENet
(本文方法)30.8809
±1.570.8261
±0.00987.3438
±0.000730.0983
±1.630.7668
±0.00918.0507
±0.000931.8705
±1.540.8613
±0.01176.5709
±0.001129.7151
±1.590.8006
±0.00878.3431
±0.0006原始图像 15.2754
±1.870.0992
±0.083443.9527
±0.007215.2147
±1.110.0922
±0.065944.2876
±0.006415.8068
±1.520.0917
±0.074441.3597
±0.005815.2147
±2.030.0922
±0.098844.2876
±0.0083 -
[1] OUAHABI A and TALEB-AHMED A. Deep learning for real-time semantic segmentation: Application in ultrasound imaging[J]. Pattern Recognition Letters, 2021, 144: 27–34. doi: 10.1016/j.patrec.2021.01.010 [2] LOUPAS T, MCDICKEN W, and ALLAN P L. An adaptive weighted median filter for speckle suppression in medical ultrasonic images[J]. IEEE transactions on Circuits and Systems, 1989, 36(1): 129–135. doi: 10.1109/31.16577 [3] GARG A and KHANDELWAL V. Despeckling of Medical Ultrasound Images Using Fast Bilateral Filter and Neighshrinksure Filter in Wavelet Domain[M]. RAWAT B, TRIVEDI A, MANHAS S, et al. Advances in Signal Processing and Communication. Singapore: Springer, 2019: 271–280. [4] YANG Qingsong, YAN Pingkun, ZHANG Yanbo, et al. Low-dose CT image denoising using a generative adversarial network with Wasserstein distance and perceptual loss[J]. IEEE Transactions on Medical Imaging, 2018, 37(6): 1348–1357. doi: 10.1109/TMI.2018.2827462 [5] SHAHDOOSTI H R and RAHEMI Z. Edge-preserving image denoising using a deep convolutional neural network[J]. Signal Processing, 2019, 159: 20–32. doi: 10.1016/j.sigpro.2019.01.017 [6] LIU Denghong, LI Jie, and YUAN Qiangqiang. A spectral grouping and attention-driven residual dense network for hyperspectral image super-resolution[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(9): 7711–7725. doi: 10.1109/TGRS.2021.3049875 [7] XIA Hao, CAI Nian, WANG Huiheng, et al. Brain MR image super-resolution via a deep convolutional neural network with multi-unit upsampling learning[J]. Signal, Image and Video Processing, 2021, 15(5): 931–939. doi: 10.1007/s11760-020-01817-x [8] MAO Xiaojiao, SHEN Chunhua, and YANG Yubin. Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections[C]. The 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 2016: 2810–2818. [9] HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 770–778. [10] CHEN Hu, ZHANG Yi, KALRA M K, et al. Low-dose CT with a residual encoder-decoder convolutional neural network[J]. IEEE Transactions on Medical Imaging, 2017, 36(12): 2524–2535. doi: 10.1109/TMI.2017.2715284 [11] CHANG Meng, LI Qi, FENG Huajun, et al. Spatial-adaptive network for single image denoising[C]. The 16th European Conference on Computer Vision, Glasgow, UK, 2020: 171–187. [12] MATEO J L and FERNÁNDEZ-CABALLERO A. Finding out general tendencies in speckle noise reduction in ultrasound images[J]. Expert Systems with Applications, 2009, 36(4): 7786–7797. doi: 10.1016/j.eswa.2008.11.029 [13] OYEDOTUN O K, AL ISMAEIL K, and AOUADA D. Training very deep neural networks: Rethinking the role of skip connections[J]. Neurocomputing, 2021, 441: 105–117. doi: 10.1016/j.neucom.2021.02.004 [14] HU Jie, SHEN Li, ALBANIE S, et al. Squeeze-and-excitation networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(8): 2011–2023. doi: 10.1109/TPAMI.2019.2913372 [15] KINGMA D P and BA J. Adam: A method for stochastic optimization[J]. arXiv: 1412.6980, 2014. [16] VAN DEN HEUVEL T L A, DE BRUIJN D, DE KORTE C L, et al. Automated measurement of fetal head circumference using 2D ultrasound images[J]. PLoS One, 2018, 13(8): e0200412. doi: 10.1371/journal.pone.0200412 [17] LECLERC S, SMISTAD E, PEDROSA J, et al. Deep learning for segmentation using an open large-scale dataset in 2D echocardiography[J]. IEEE Transactions on Medical Imaging, 2019, 38(9): 2198–2210. doi: 10.1109/TMI.2019.2900516 [18] BURGER H C, SCHULER C J, and HARMELING S. Image denoising: Can plain neural networks compete with BM3D?[C]. 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, USA, 2012: 2392–2399. [19] DABOV K, FOI A, KATKOVNIK V, et al. Image denoising by sparse 3-D transform-domain collaborative filtering[J]. IEEE Transactions on Image Processing, 2007, 16(8): 2080–2095. doi: 10.1109/TIP.2007.901238 [20] CHEN Yang, YIN Xindao, SHI Luyao, et al. Improving abdomen tumor low-dose CT images using a fast dictionary learning based processing[J]. Physics in Medicine & Biology, 2013, 58(16): 5803–5820. doi: 10.1088/0031-9155/58/16/5803 [21] CHEN Hu, ZHANG Yi, ZHANG Weihua, et al. Low-dose CT via convolutional neural network[J]. Biomedical Optics Express, 2017, 8(2): 679–694. doi: 10.1364/BOE.8.000679 [22] ZHANG Yulun, TIAN Yapeng, KONG Yu, et al. Residual dense network for image restoration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(7): 2480–2495. doi: 10.1109/TPAMI.2020.2968521 -





 下载:
下载:







 下载:
下载:
