Research on the Security Characteristic and Metric Method for Ring Oscillatro-based True Random Number Generator under Fault Disturbance
-
摘要: 作为密码安全性的根源,在各类密码体制和系统中,真随机数起着不可替代的重要作用。现实中,真随机数往往基于随机物理过程实现,从而使其可能遭受环境引入或攻击者恶意施加的影响,造成随机数生成质量的下降,进而对密码应用安全性产生威胁。该文以当前广泛应用的基于振荡环的真随机数发生器(RO-TRNG)为对象,对故障注入场景下,熵源和熵抽取部分受到的影响及由此造成的安全性变异进行了深入分析和研究,并基于捕获偏置度提出了能够充分反映故障扰动场景下RO-TRNG安全特性的度量模型。实验表明,该度量模型能够很好地反映在遭受故障扰动时,RO-TRNG在抖动方差累积和节拍延迟链上升沿捕获概率偏置等方面受到的影响,并对RO-TRNG在高危复杂环境下的安全性实施客观分析。Abstract: As the source of the cipher security, the true random number plays an important and irreplaceable role in kinds of cipher systems. In practice, the true random number is usually generated in the random physic processes, and it is vulnerable to the malicious attack, caused by the environment. Thus the poorer quality of the random number makes the cryptographic application security under threat. In order to research the Ring Oscillator-based True Random Number Generator(RO-TRNG), which is widely used currently, the impact on its entropy source and extract is further analyzed and researched, as well as the resulting security variation, in the fault injection attack scenario. Based on the acquisition bias degree, the RO-TRNG security metric model in the scenario of the fault disturbance, is prompted. It is experimented that, while exposed to the fault disturbance environment, the impact on the accumulation of the vibration variance and the bias on the acquistion probability of the rising edge of the beat delay chain for RO-TRNG, can be fully reflected by the model, and the RO-TRNG security can be analyzed objectively, while exposed to the highly dangerous and complicated environment.
-
表 1 不同序号捕获概率变化趋势
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 $ {P_{{L_1}}} $ 0.5 0.6 0.7 0.8 0.823 0.836 0.845 0.862 0.894 0.912 0.935 0.946 0.957 0.969 0.972 $ {P_{{L_0}}} $ 0.5 0.4 0.3 0.2 0.177 0.164 0.155 0.138 0.106 0.088 0.065 0.054 0.043 0.031 0.028 表 2 方差累积特性测量结果
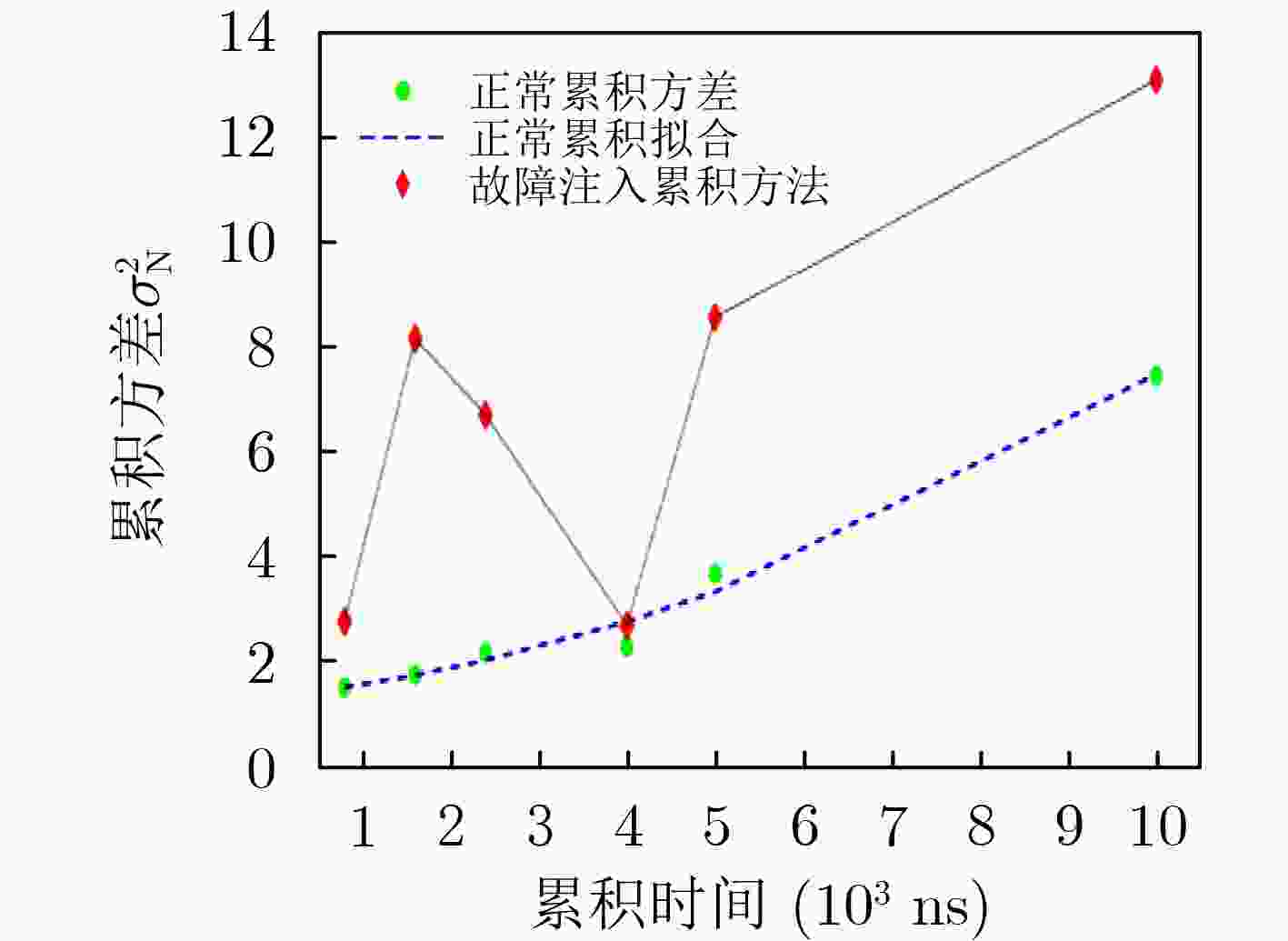
参数测量值 正常
情况$ {t_N} $( ns) 800 1600 2400 4000 5000 10000 $ \sigma _N^2 $ 1.4959 1.7244 2.1507 2.2688 3.6597 7.4597 故障
注入$ {t_N} $( ns) 800 1600 2400 4000 5000 10000 $ \hat \sigma _N^2 $ 2.7425 8.1582 6.7073 2.6719 8.5677 13.1086 -
[1] DUMONT M, LISART M, and MAURINE P. Electromagnetic fault injection: How faults occur[C]. 2019 Workshop on Fault Diagnosis and Tolerance in Cryptography (FDTC), Atlanta, USA, 2019: 9–16. [2] GAY M, PAXIAN T, UPADHYAYA D, et al. . Hardware-oriented algebraic fault attack framework with multiple fault injection support[C]. 2019 Workshop on Fault Diagnosis and Tolerance in Cryptography (FDTC), Atlanta, USA, 2019: 25–32. [3] GRUBER M, PROBST M, and TEMPELMEIER M. Persistent fault analysis of OCB, DEOXYS and COLM[C]. 2019 Workshop on Fault Diagnosis and Tolerance in Cryptography (FDTC), Atlanta, USA, 2019: 17–24. [4] DAEMEN J, DOBRAUNIG C, EICHLSEDER M, et al. Protecting against statistical ineffective fault attacks[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2020(3): 508–543. [5] MARKETTOS A T and MOORE S W. The frequency injection attack on ring-oscillator-based true random number generators[C]. 11th International Workshop on Cryptographic Hardware and Embedded Systems, Lausanne, Switzerland, 2009: 317–331. [6] BAYON P, BOSSUET L, AUBERT A, et al. . Contactless electromagnetic active attack on ring oscillator based true random number generator[C]. Third International Workshop on Constructive Side-Channel Analysis and Secure Design, Darmstadt, Germany, 2012: 151–166. [7] BAYON P, BOSSUET L, AUBERT A, et al. . Electromagnetic analysis on ring oscillator-based true random number generators[C]. 2013 IEEE International Symposium on Circuits and Systems (ISCAS), Beijing, China, 2013: 1954–1957. [8] BAUDET M, LUBICZ D, MICOLOD J, et al. On the security of oscillator-based random number generators[J]. Journal of Cryptology, 2011, 24(2): 398–425. doi: 10.1007/s00145-010-9089-3 [9] BÉRINGUIER-BOHER N, BEROULLE V, HÉLY D, et al. Clock generator behavioral modeling for supply voltage glitch attack effects analysis[J]. Microprocessors and Microsystems, 2016, 47: 37–43. doi: 10.1016/j.micpro.2016.02.014 [10] MADAU M, AGOYAN M, BALASCH J, et al. . The impact of pulsed Electromagnetic fault injection on true random number generators[C]. 2018 Workshop on Fault Diagnosis and Tolerance in Cryptography (FDTC), Amsterdam, Holland, 2018: 43–48. [11] GUILLEY S and EL HOUSNI Y. Random numbers generation: Tests and attacks[C]. 2018 Workshop on Fault Diagnosis and Tolerance in Cryptography (FDTC), Amsterdam, Holland, 2018: 49–54. [12] EPSTEIN M, HARS L, KRASINSKI R, et al. . Design and implementation of a true random number generator based on digital circuit artifacts[C]. 5th International Workshop on Cryptographic Hardware and Embedded Systems, Cologne, Germany, 2003: 152–165. [13] PARESCHI F, SETTI G, and ROVATTI R. A fast chaos-based true random number generator for cryptographic applications[C]. 2006 Proceedings of the 32nd European Solid-State Circuits Conference, Montreaux, Switzerland, 2006: 130–133. [14] 魏子魁, 胡毅, 金鑫, 等. 一种低功耗高噪声源真随机数设计[J]. 电子与信息学报, 2020, 42(10): 2566–2572. doi: 10.11999/JEIT190719WEI Zikui, HU Yi, JIN Xin, et al. A true random number design of low power and high noise source[J]. Journal of Electronics &Information Technology, 2020, 42(10): 2566–2572. doi: 10.11999/JEIT190719 [15] ROZIC V, YANG Bohan, DEHAENE W, et al. . Highly efficient entropy extraction for true random number generators on FPGAs[C]. The 52nd Annual Design Automation Conference, San Francisco, USA, 2015: 116. [16] GRUJIĆ M, ROŽIĆ V, YANG Bohan, et al. . A closer look at the delay-chain based TRNG[C]. 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 2018: 1–5. [17] YANG Bohan, ROŽIC V, GRUJIC M, et al. ES-TRNG: A high-throughput, low-area true random number generator based on edge sampling[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2018, 2018(3): 267–292. [18] HADDAD P, TEGLIA Y, BERNARD F, et al. . On the assumption of mutual independence of jitter realizations in P-TRNG stochastic models[C]. 2014 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 2014: 1–6. [19] BOZZATO C, FOCARDI R, and PALMARINI F. Shaping the glitch: Optimizing voltage fault injection attacks[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2019(2): 199–224. [20] 欧庆于, 罗芳, 吴晓平, 等. 基于电压毛刺故障扰动的分组密码安全性度量方法研究[J]. 电子学报, 2021, 49(3): 417–423. doi: 10.12263/DZXB.20200514OU Qingyu, LUO Fang, WU Xiaoping, et al. Research on the metric method for the security of the block cipher based on the voltage glitch fault disturbance[J]. Acta Electronica Sinica, 2021, 49(3): 417–423. doi: 10.12263/DZXB.20200514 [21] ALLINI E N, SKÓRSKI M, PETURA O, et al. Evaluation and monitoring of free running oscillators serving as source of randomness[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2018, 2018(3): 214–242. [22] YANG Bohan, ROŽIĆ V, GRUJIĆ M, et al. . On-chip jitter measurement for true random number generators[C]. 2017 Asian Hardware Oriented Security and Trust Symposium (AsianHOST). Beijing, China, 2017: 91–96. [23] 国家密码管理局. GM/T 0005-2012 随机性检测规范[S]. 北京: 中国标准出版社, 2012.National Cryptography Administration. GM/T 0005-2012 Randomness test specification[S]. Beijing: China Standard Press, 2012. [24] NIST. NIST Statistical Test Suite[EB/OL]. http://www.doc88.com/p-3126997400376.html, 2021. -





 下载:
下载:



 下载:
下载:
