Binary Spreading Sequences of Lengths Non-Power-of-Two for Uplink Grant-Free Non-Orthogonal Multiple Access
-
摘要: 为了解决5G大规模机器类通信场景下大规模接入和如何提高频谱效率的问题,该文针对免调度非正交多址接入(NOMA)系统上行链路,通过采用插入函数在2元Golay序列上插入元素的方法,提出具有低峰均功率比(PAPR)且长度为非2幂次的2元扩频序列集。仿真结果表明,得到的序列集具有低相干性,这为基于压缩感知的活跃用户检测提供了可靠的性能。同传统的Zadoff-Chu序列相比,新型2元序列集具有更小的字符集,便于实现。此外,所构造的序列PAPR最大为4,低于高斯随机序列和Zadoff-Chu序列,因此可以有效解决时域信号峰均功率比过高的问题。Abstract: In order to solve the problem of mass access and how to improve spectrum efficiency in 5G massive Machine-Type Communication (mMTC) scenario, for the uplink grant-free Non-Orthogonal Multi-Access(NOMA) system, new sets of non-orthogonal binary spreading sequences with low Peak Average Power Ratio(PAPR) and lengths non-power-of-two is proposed by inserting elements into binary Golay sequences using insertion function. Simulation results confirm that the resulting sequence sets has low coherence, which provides reliable performance for active user detection based on Compressed Sensing (CS). Compared with the traditional Zadoff-chu sequences, the new binary sequence sets has a smaller alphabet set, which is easy to implement. Moreover, the resultanted sequences exhibit the PAPR of at most 4, which is lower than those for Gaussian and Zadoff-Chu sequences. Therefore, the problem of high peak-to-power ratio in time domain can be solved effectively.
-
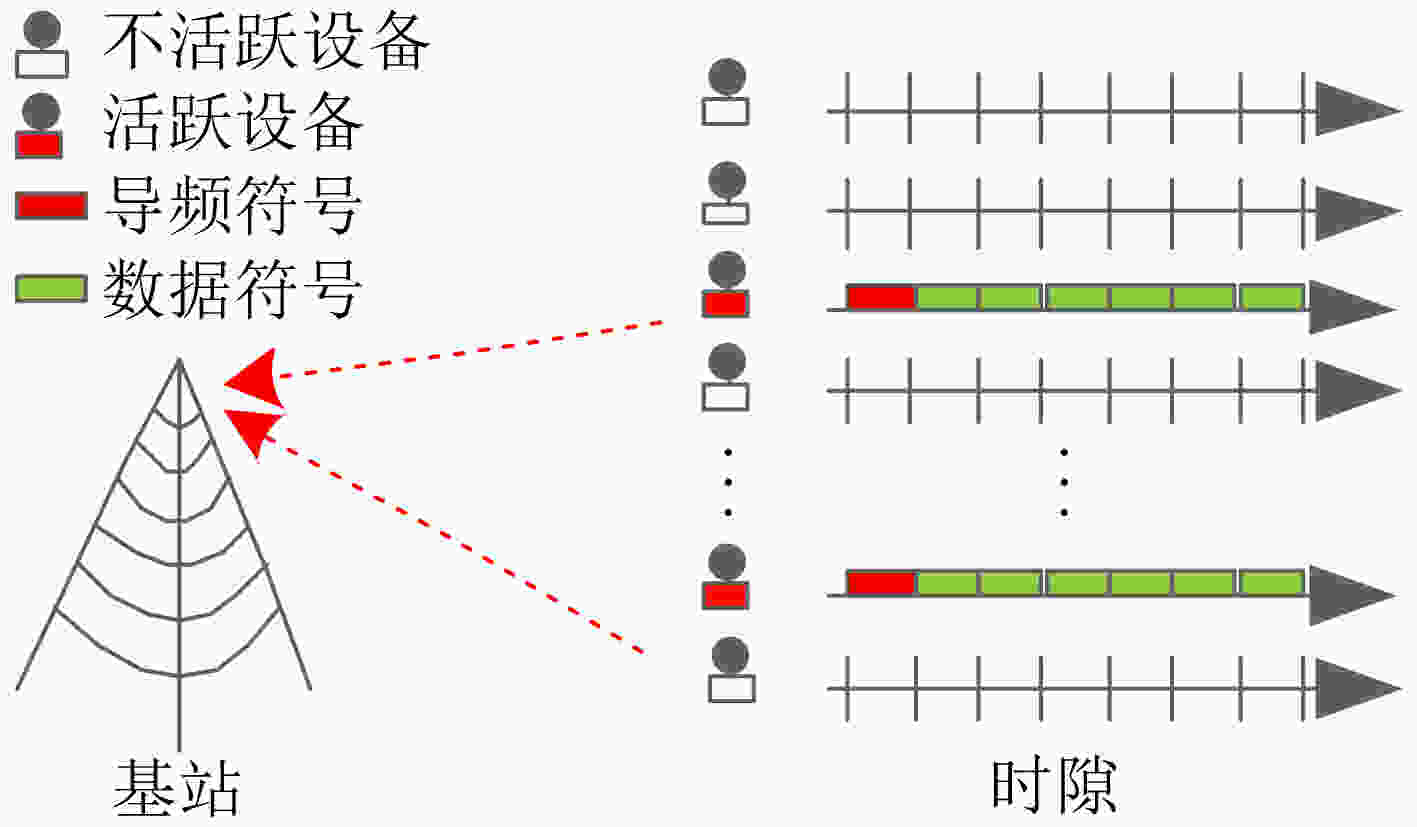
图 1 上行免调度NOMA的系统模型[21]
表 1 使
${{\boldsymbol{\varPhi}} '}$ 达到最优的置换集$ {M'}{\text{ = }}{{\text{2}}^m} $ 用户过载因子 相干值 置换集$\varGamma$ 32 $ 2 \le L \le 8 $ 0.25 $(5,4,3,2,1),(3,4,2,5,1),(4,2,5,3,1),(4,3,5,1,2),(4,5,1,3,2),(5,3,1,4,2),(5,4,2,1,3),(4,1,2,5,3)$ 64 $ 2 \le L \le 5 $ 0.125 $(3,4,5,2,6,1),(6,3,2,4,1,5),(4,1,6,5,2,3),(6,5,3,1,2,4),(5,3,2,1,6,4)$ 128 $ 2 \le L \le 8 $ 0.125 $\begin{array}{l} {\text{(4,5,1,3,6,7,2),(4,2,5,1,6,7,3),(6,7,1,2,3,5,4),(5,3,6,4,1,7,2),(6,4,7,3,1,5,2),(4,3,6,7,5,2,1),} } \\ {\text{(6,1,3,2,7,4,5),(6,7,5,1,4,3,2)} } \\ \end{array}$ 256 $ 2 \le L \le 5 $ 0.0625 ${\text{(4,5,6,1,3,7,8,2),(7,6,8,2,3,1,4,5),(7,1,8,6,4,3,5,2),(6,7,2,3,8,4,1,5),(8,3,1,5,2,7,4,6)} }$ 512 $ 2 \le L \le 8 $ 0.0625 $\begin{array}{l} {\text{(8,3,7,4,9,2,5,1,6),(8,4,3,7,2,6,1,9,5),(9,5,4,1,6,8,3,7,2),(6,5,8,7,9,3,4,2,1),} } \\ {\text{(4,1,7,6,8,9,2,5,3),(4,8,2,6,9,7,5,3,1),(5,3,7,8,2,1,6,9,4),(5,6,9,3,7,1,8,2,4)} } \\ \end{array}$ 1024 $ 2 \le L \le 5 $ 0.03125 $\begin{array}{l} {\text{(9,1,6,3,2,8,5,4,10,7),(5,1,9,8,2,10,6,3,7,4),(6,3,8,10,9,7,1,5,4,2),(7,6,8,1,3,2,10,9,4,5),} } \\ {\text{(9,5,3,2,4,8,6,10,7,1)} } \\ \end{array}$ 表 2 扩频矩阵相干值
$\mu ({\boldsymbol{\varPhi}} )$ 扩频矩阵 序列长度 $\mu ({\boldsymbol{\varPhi} } )$ 扩频矩阵 序列长度 $\mu ({\boldsymbol{\varPhi} } )$ 扩频矩阵 序列长度 $\mu ({\boldsymbol{\varPhi } })$ 扩频矩阵 序列长度 $\mu ({\boldsymbol{\varPhi } })$ 本文 33 0.2727 本文 34 0.2941 文献[16] 32 0.2500 基于ZC序列 31 0.1796 65 0.1385 66 0.1515 64 0.1250 61 0.1280 129 0.1318 130 0.1385 128 0.1250 127 0.0887 257 0.0661 258 0.0698 256 0.0625 257 0.0624 513 0.0643 514 0.0661 512 0.0625 509 0.0443 1025 0.0322 1026 0.0331 1024 0.03125 1021 0.0313 表 3 扩频矩阵里序列的最大PAPR
扩频矩阵 序列长度 PAPR 扩频矩阵 序列长度 PAPR 扩频矩阵 序列长度 PAPR 扩频矩阵 序列长度 PAPR 本文 33 2.4545 本文 34 2.9412 文献[16] 32 2.0000 基于ZC序列 31 4.4066 65 2.2825 66 2.6172 64 1.9928 61 4.0922 129 2.2403 130 2.4923 128 2.0000 127 4.3376 257 2.1699 258 2.3265 256 1.9978 257 4.7396 513 2.1228 514 2.2490 512 2.0000 509 4.8785 1025 2.0834 1026 2.1713 1024 1.9993 1021 5.2751 表 4 几种确定性扩频矩阵的参数
扩频矩阵 扩频序列长度$ M $ $\mu ({\boldsymbol{\varPhi} } )$ PAPR上界 字符集大小 文献[16] $ {2^m} $ $\sqrt{{1}/{ {2}^{m\text{-1} } } },\;\;m{\text{为奇数} }$
$\sqrt{{1}/{ {2}^{m} } },\;m{\text{为偶数} }$2 2 基于ZC序列 $ {M_{{\text{zc}}}} $为任意素数 $\sqrt {{1}/{ { {M_{ {\text{zc} } } } } } }$ >4 $ {M_{{\text{zc}}}} $ 本文 $ {2^m}{\text{ + }}1 $ $\dfrac{\sqrt{ {2}^{m+1} }+1}{ {2}^{m}+1},\;m{\text{为奇数} }$
$\dfrac{\sqrt{ {2}^{m} }+1}{ {2}^{m}+1},\;m{\text{为偶数} }$4 2 本文 $ {2^m}{\text{ + 2}} $ $ \dfrac{\sqrt{{2}^{m+1}}+2}{{2}^{m}+2},m{\text{为奇数}} $,$ \dfrac{\sqrt{{2}^{m}}+2}{{2}^{m}+2},m{\text{为偶数}} $ 4 2 -
[1] 戴维佳. mMTC非正交多址接入中的活跃用户检测和信道估计[D]. [硕士论文], 中国科学技术大学, 2019.DAI Weijia. Active user detection and channel estimation in Non-orthogonal multiple access of mMTC[D]. [Master dissertation], University of Science and Technology of China, 2019. [2] 王茜竹, 方冬, 吴广富. 基于改进稀疏度自适应匹配算法的免授权非正交多址接入上行传输多用户检测[J]. 电子与信息学报, 2020, 42(9): 2216–2222. doi: 10.11999/JEIT190505WANG Qianzhu, FANG Dong, and WU Guangfu. Multi-user detection based on sparsity adaptive matching pursuit compressive sensing for uplink grant-free non-orthogonal multiple access[J]. Journal of Electronics &Information Technology, 2020, 42(9): 2216–2222. doi: 10.11999/JEIT190505 [3] TALEB T and KUNZ A. Machine type communications in 3GPP networks: Potential, challenges, and solutions[J]. IEEE Communications Magazine, 2012, 50(3): 178–184. doi: 10.1109/MCOM.2012.6163599 [4] SHAHAB M B, ABBAS R, SHIRVANIMOGHADDAM M, et al. Grant-free non-orthogonal multiple access for IoT: A survey[J]. IEEE Communications Surveys & Tutorials, 2020, 22(3): 1805–1838. doi: 10.1109/COMST.2020.2996032 [5] 戴维佳, 李乐天, 周武旸. 基于期望传播的活跃用户检测和信道估计[J]. 中国科学技术大学学报, 2019, 49(10): 797–804, 819. doi: 10.3969/j.issn.0253-2778.2019.10.004DAI Weijia, LI Letian, and ZHOU Wuyang. Active user detection and channel estimation based on expectation propagation[J]. Journal of University of Science and Technology of China, 2019, 49(10): 797–804, 819. doi: 10.3969/j.issn.0253-2778.2019.10.004 [6] DING Zhiguo, LEI Xianfu, KARAGIANNIDIS G K, et al. A survey on non-orthogonal multiple access for 5G networks: Research challenges and future trends[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(10): 2181–2195. doi: 10.1109/JSAC.2017.2725519 [7] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582 [8] CAI Donghong, WEN Jinming, FAN Pingzhi, et al. Active user and data detection for uplink grant-free NOMA systems[J]. China Communications, 2020, 17(11): 12–28. doi: 10.23919/JCC.2020.11.002 [9] HOSOKAWA S, TEO K, OHNO S, et al. Pilot tone design with low peak-to-average power ratio in OFDM[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2005, E88-A(8): 2117–2123. doi: 10.1093/ietfec/e88-a.8.2117 [10] LIU Liang, LARSSON E G, YU Wei, et al. Sparse signal processing for grant-free massive connectivity: A future paradigm for random access protocols in the internet of things[J]. IEEE Signal Processing Magazine, 2018, 35(5): 88–99. doi: 10.1109/MSP.2018.2844952 [11] CHEN Huan, FAN Pingzhi, and LI Li. Active users detection based on deterministic sequences for massive connectivity[C]. 2019 Ninth International Workshop on Signal Design and its Applications in Communications (IWSDA), Dongguan, China, 2019: 1–5. doi: 10.1109/IWSDA46143.2019.8966106. [12] YANG K, KIM Y K, and KUMAR P V. Quasi-orthogonal sequences for code-division multiple-access systems[J]. IEEE Transactions on Information Theory, 2000, 46(3): 982–993. doi: 10.1109/18.841175 [13] WEN Yang, HUANG Wei, and ZHANG Zhongpei. CAZAC sequence and its application in LTE random access[C]. 2006 IEEE Information Theory Workshop - ITW '06 Chengdu, Chengdu, China, 2006: 544–547. doi: 10.1109/ITW2.2006.323692. [14] LI Zhen, SUN Teng, LU Guangyue, et al. Preamble design and detection for 5G enabled satellite random access[J]. IEEE Access, 2020, 8: 49873–49884. doi: 10.1109/ACCESS.2020.2979871 [15] PITAVAL R A, POPOVIĆB M, WANG Peng, et al. Overcoming 5G PRACH capacity shortfall: Supersets of Zadoff–Chu sequences with low-correlation zone[J]. IEEE Transactions on Communications, 2020, 68(9): 5673–5688. doi: 10.1109/TCOMM.2020.3003664 [16] YU N Y. Binary Golay spreading sequences and reed-Muller codes for uplink grant-free NOMA[J]. IEEE Transactions on Communications, 2021, 69(1): 276–290. doi: 10.1109/TCOMM.2020.3031613 [17] ADHIKARY A R and MAJHI S. New constructions of complementary sets of sequences of lengths non-power-of-two[J]. IEEE Communications Letters, 2019, 23(7): 1119–1122. doi: 10.1109/LCOMM.2019.2913382 [18] LIU Zilong, PARAMPALLI U, and GUAN Yongliang, et al. Optimal odd-length binary Z-complementary pairs[J]. IEEE Transactions on Information Theory, 2014, 60(9): 5768–5781. doi: 10.1109/TIT.2014.2335731 [19] ADHIKARY A R, MAJHI S, LIU Zilong, et al. New sets of even-length binary Z-complementary pairs with asymptotic ZCZ ratio of 3/4[J]. IEEE Signal Processing Letters, 2018, 25(7): 970–973. doi: 10.1109/LSP.2018.2834143 [20] DAVIS J A and JEDWAB J. Peak-to-mean power control in OFDM, Golay complementary sequences, and Reed-Muller codes[J]. IEEE Transactions on Information Theory, 1999, 45(7): 2397–2417. doi: 10.1109/18.796380 [21] AHN J, SHIM B, and LEE K B. EP-based joint active user detection and channel estimation for massive machine-type communications[J]. IEEE Transactions on Communications, 2019, 67(7): 5178–5189. doi: 10.1109/TCOMM.2019.2907853 [22] 3GPP. 3GPP TS-36.211 V13. 2.0 3rd Generation partnership project; technical specification group radio access network; Evolved Universal Terrestrial Radio Access (E-UTRA); physical channels and modulation[S]. France: 3GPP, 2016. [23] WANG Bichai, DAI Linglong, MIR T, et al. Joint user activity and data detection based on structured compressive sensing for NOMA[J]. IEEE Communications Letters, 2016, 20(7): 1473–1476. doi: 10.1109/LCOMM.2016.2560180 [24] DU Yang, DONG Binhong, ZHU Wuyong, et al. Joint channel estimation and multiuser detection for uplink grant-free NOMA[J]. IEEE Wireless Communications Letters, 2018, 7(4): 682–685. doi: 10.1109/LWC.2018.2810278 [25] TROPP J A, GILBERT A C, and STRAUSS M J. Algorithms for simultaneous sparse approximation. Part I: Greedy pursuit[J]. Signal Processing, 2006, 86(3): 572–588. doi: 10.1016/j.sigpro.2005.05.030 -





 下载:
下载:
















 下载:
下载:
