基于指数-余弦离散混沌映射的图像加密算法研究

刘思聪; 李春彪; 李泳新

doi:10.11999/JEIT210270

基于指数-余弦离散混沌映射的图像加密算法研究

doi: 10.11999/JEIT210270

刘思聪^{1, 2},
李春彪^3, ,,
李泳新³

1.
电子科技大学生命科学学院成都 610054
2.
江苏经贸职业技术学院智能工程学院南京 210045
3.
南京信息工程大学人工智能学院南京 210044

详细信息

作者简介:
刘思聪：男，1986年生，讲师，研究方向为离散混沌系统与信息安全、神经网络与智能信息处理

李春彪：男，1971年生，教授，研究方向为混沌系统、忆阻神经形态电路与网络及其应用

李泳新：男，1997年生，硕士生，研究方向为离散混沌系统、忆阻神经网络与应用

通讯作者:
李春彪　chunbiaolee@nuist.edu.cn; goontry@126.com

中图分类号: TN911.73; TN918.4
计量
- 文章访问数: 1622
- HTML全文浏览量: 554
- PDF下载量: 193
- 被引次数: 0
出版历程
- 收稿日期: 2021-04-02
- 修回日期: 2021-11-17
- 录用日期: 2021-11-25
- 网络出版日期: 2021-11-26
- 刊出日期: 2022-05-25

A Novel Image Encryption Algorithm Based on Exponent-cosine Chaotic Mapping

LIU Sicong^{1, 2},
LI Chunbiao^{3
, ,},
LI Yongxing³

1.
School of Life Science, University of Electronic Science and Technology of China, Chengdu 610054, China
2.
School of Artificial Intelligence and Engineering, Jiangsu Vocational Institute of Commerce, Nanjing 210045, China
3.
School of Artificial Intelligence, Nanjing University of Information Science and Technology, Nanjing 210044, China

摘要

摘要: 为了增强图像数据传输的安全性，该文提出一种新型的2维指数-余弦离散混沌映射系统。该系统通过向1维余弦混沌系统中引入指数和高次幂非线性项来构造新型混沌映射。引入的非线性项对1维余弦混沌系统的迭代过程进行扰动得到更饱满的混沌相轨。利用Lyapunov指数谱、系统分岔图等对该系统的混沌动力学性质进行了验证。基于此混沌映射，该文提出一种新型的混沌图像加密算法。该算法通过“置乱-扩散-置乱”等加密环节，使得加密后的数据具有很好的数据安全性。加密图像数据的安全性分析也表明2维指数-余弦混沌映射具有较强的算法鲁棒性以及加密安全性。
- 图像加密 /
- 2维离散混沌映射 /
- 算法鲁棒性 /
- 加密安全性检验
Abstract: In order to enhance the security of image data transmission, a novel two-dimensional exponent - cosine chaotic map is proposed. In this system, a new chaotic map is constructed by introducing exponent and high-power nonlinear terms into one dimensional cosine chaotic system. The nonlinear term is introduced to perturb the iterative process of one-dimensional cosine chaotic system to obtain fuller chaotic phase orbits. Lyapunov exponential spectrum and system bifurcation diagram are used to verify the features of chaotic system. Based on the chaotic map, a novel image encryption algorithm is proposed. The encrypted data has good encryption security by following a “scrambling-diffusion-scrambling” strategy. Security analysis of encrypted image data also shows that the two-dimensional exponential - cosine chaotic map has strong robustness and encryption security.
- Image encryption /
- Two-dimensional chaotic map /
- Algorithm robustness /
- Encryption security checking

HTML全文

图 1 动力学系统在不同初始值下特征值分布图

下载: 全尺寸图片幻灯片

图 2 李雅普诺夫指数谱和分叉图

下载: 全尺寸图片幻灯片

图 3 系统动力学系统典型相轨图

下载: 全尺寸图片幻灯片

图 4 2D-ECs混沌加密系统加密算法流图

下载: 全尺寸图片幻灯片

图 5 2D-ECs混沌加密图像及直方图信息

下载: 全尺寸图片幻灯片

图 6 随机像素点移除

下载: 全尺寸图片幻灯片

图 7 彩色图像加解密效果图

下载: 全尺寸图片幻灯片

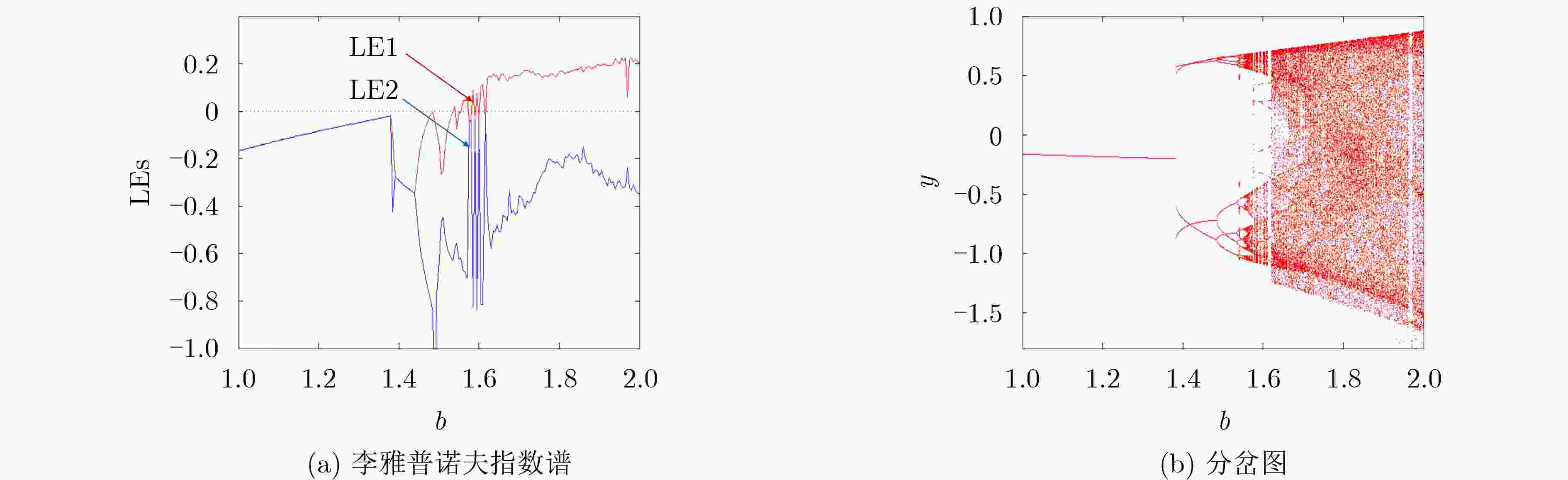
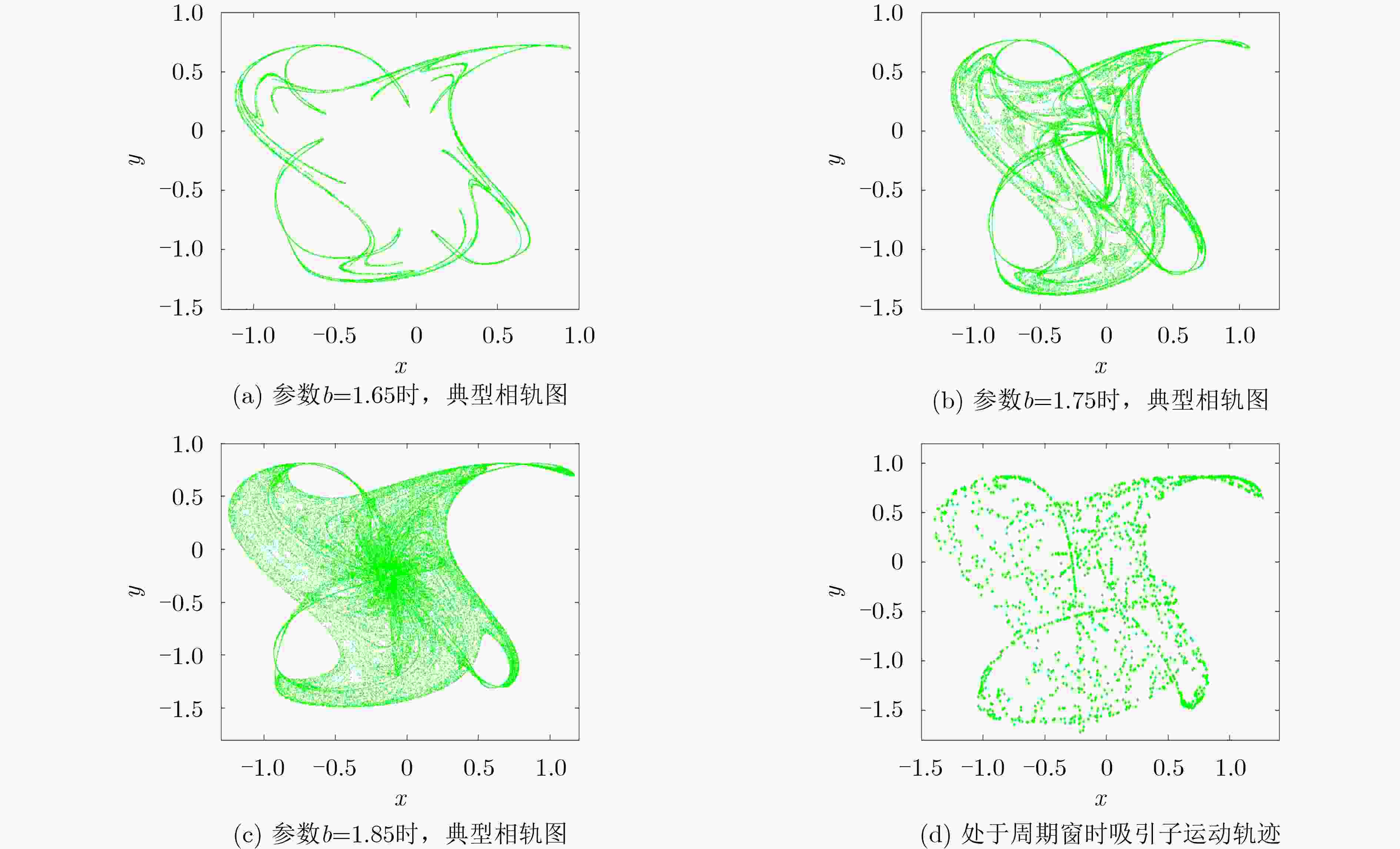
表 1 不同参数b对应的李雅普诺夫指数谱及吸引子类型

b	李雅普诺夫指数谱	吸引子类型
1.65	0.1301, –0.4619	混沌吸引子
1.75	0.1580, –0.2573	混沌吸引子
1.85	0.1781, –0.2180	混沌吸引子
1.97	–0.1155, –0.1155	离散周期点

下载: 导出CSV

表 2 算法时间复杂度分析

算法名称	时间复杂度
2D-ECs	O(n)
文献[11]	O(n²)
文献[12]	O(nlgn)
文献[13]	O(n²)

下载: 导出CSV

表 3 NPCR,UACI参数值(%)

灰度图像	2D-ECs		文献[12]		文献[13]		文献[14]
灰度图像	NPCR	UACI	NPCR	UACI	NPCR	UACI	NPCR	UACI
Cameraman	99.610	33.464	–	–	–	–	99.72	33.36
Lena	99.611	33.466	–	–	99.66	33.520	–	–
Boat	99.615	33.467	99.190	33.400	–	–	–	–

下载: 导出CSV

表 4 自相关系数

图像	方位角	原始值	加密后
Boat	左	0.87986	–0.0029753
	右	0.87578	0.00099645
	上	0.89982	–0.00026347
	下	0.89718	–0.00096155
	左上	0.81343	–0.00034887
	左下	0.82413	–0.00022197
	右上	0.83087	0.00025217
	右下	0.80362	–2.4882e-05
Cameraman	左	0.91761	0.0006906
	右	0.92347	0.00017951
	上	0.95272	–0.00039079
	下	0.95336	0.00040691
	左上	0.88771	–0.00042397
	左下	0.90207	3.8675e-05
	右上	0.90196	0.00051293
	右下	0.88703	0.00053786
Lena	左	0.94044	–0.00029284
	右	0.93955	–0.00011737
	上	0.96882	0.00014822
	下	0.97068	–0.00053991
	左上	0.91482	–0.00088227
	左下	0.94011	0.00059065
	右上	0.93857	–0.00044307
	右下	0.91636	1.7261e-05

下载: 导出CSV

表 5 图像信息熵

图像	信息熵
Boat	7.9958
Cameraman	7.9944
Lena	7.9951

下载: 导出CSV

参考文献(15)

[1]	MATTHEWS R. On the derivation of a “Chaotic” encryption algorithm[J]. Cryptologia, 1989, 13(1): 29–42. doi: 10.1080/0161-118991863745
[2]	STOYANOV B and KORDOV K. Image encryption using Chebyshev map and rotation equation[J]. Entropy, 2015, 17(4): 2117–2139. doi: 10.3390/e17042117
[3]	HUANG Xiaoling. Image encryption algorithm using chaotic chebyshev generator[J]. Nonlinear Dynamics, 2012, 67(4): 2411–2417. doi: 10.1007/s11071-011-0155-7
[4]	MURILLO-ESCOBAR M A, CRUZ-HERNÁNDEZ C, ABUNDIZ-PÉREZ F, et al. A RGB image encryption algorithm based on total plain image characteristics and chaos[J]. Signal Processing, 2015, 109: 119–131. doi: 10.1016/j.sigpro.2014.10.033
[5]	吕群, 薛伟. 结合混沌系统和动态S-盒的图像加密算法[J]. 小型微型计算机系统, 2018, 39(3): 607–613. doi: 10.3969/j.issn.1000-1220.2018.03.038 LV Qun and XUE Wei. Image encryption algorithm combining chaotic system and dynamic S-boxes[J]. Journal of Chinese Computer Systems, 2018, 39(3): 607–613. doi: 10.3969/j.issn.1000-1220.2018.03.038
[6]	HUA Zhongyun and ZHOU Yicong. One-dimensional nonlinear model for producing chaos[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2018, 65(1): 235–246. doi: 10.1109/TCSI.2017.2717943
[7]	ZHOU Yicong, BAO Long, and CHEN C L P. Image encryption using a new parametric switching chaotic system[J]. Signal Processing, 2013, 93(11): 3039–3052. doi: 10.1016/j.sigpro.2013.04.021
[8]	LIU Yang, TONG Xiaojun, and HU Shicheng. A family of new complex number chaotic maps based image encryption algorithm[J]. Signal Processing:Image Communication, 2013, 28(10): 1548–1559. doi: 10.1016/j.image.2013.07.009
[9]	HUA Zhongyun and ZHOU Yicong. Image encryption using 2D logistic-adjusted-sine map[J]. Information Sciences, 2016, 339: 237–253. doi: 10.1016/j.ins.2016.01.017
[10]	GAN Zhihua, CHAI Xiuli, HAN Daojun, et al. A chaotic image encryption algorithm based on 3-D bit-plane permutation[J]. Neural Computing and Applications, 2019, 31(11): 7111–7130. doi: 10.1007/s00521-018-3541-y
[11]	YIN Qi and WANG Chunhua. A new chaotic image encryption scheme using breadth-first search and dynamic diffusion[J]. International Journal of Bifurcation and Chaos, 2018, 28(4): 1850047. doi: 10.1142/S0218127418500475
[12]	LUO Yuqin, YU Jin, LAI Wenrui, et al. A novel chaotic image encryption algorithm based on improved baker map and logistic map[J]. Multimedia Tools and Applications, 2019, 78(15): 22023–22043. doi: 10.1007/s11042-019-7453-3
[13]	KHAN M and MASOOD F. A novel chaotic image encryption technique based on multiple discrete dynamical maps[J]. Multimedia Tools and Applications, 2019, 78(18): 26203–26222. doi: 10.1007/s11042-019-07818-4
[14]	YE Guodong, PAN Chen, HUANG Xiaoling, et al. An efficient pixel-level chaotic image encryption algorithm[J]. Nonlinear Dynamics, 2018, 94(1): 745–756. doi: 10.1007/s11071-018-4391-y
[15]	LIU Lidong, LEI Yuhang, and WANG Dan. A fast chaotic image encryption scheme with simultaneous permutation-diffusion operation[J]. IEEE Access, 2020, 8: 27361–27374. doi: 10.1109/ACCESS.2020.2971759