Optimization of the Transmit Weighting Matrix for MIMO Radar Based on the Uniform Elemental Power Constraint
-
摘要: 为提高多输入多输出(MIMO)雷达的目标角度估计性能,同时兼顾雷达发射功率利用率的需求,该文以合成发射导向矢量与期望导向矢量二范数误差为目标函数,研究了阵元等功率约束下的发射加权矩阵优化问题。推导了发射加权矩阵向量化条件下的等价优化模型,并基于循环优化方法和改进PDR算法对其进行了求解。在每次迭代过程中,所提方法均能获得子优化问题的闭式解,因而其计算复杂度非常低。在此基础之上,从理论上证明了所提方法的收敛性。由于该方法实现了MIMO雷达发射功率在期望空域的聚焦,在同等条件下相比传统MIMO雷达能够有效提高目标的角度估计性能。最后,仿真实验表明了所提方法的有效性。Abstract: To improve the angle estimation performance of the MIMO (Multiple-Input-Multiple-Output) radar, the optimization of the transmit weighting matrix by setting the 2-norm error between the actual synthesized transmitting steering vector and the desired one as the objective function is studied in this paper. The maximization of the transmit power utilization can be enforced via imposing the uniform elemental power constraint on the formulation. Furthermore, a method based on the cyclic algorithm and improved Projection Descent and Retraction (PDR) is provided to settle the equivalent problem under the vectorization of the transmit weighting matrix. The closed solution can be achieved at each iteration, then the computational complexity is low of the proposed method. And the convergence can also be proved. The proposed method obtains the superior performance in angle estimation of MIMO radar based on focusing the transmit power into the desired spatial sector. Finally, simulation results are presented to verify the efficiency of the proposed method.
-
表 1 所提算法的具体流程
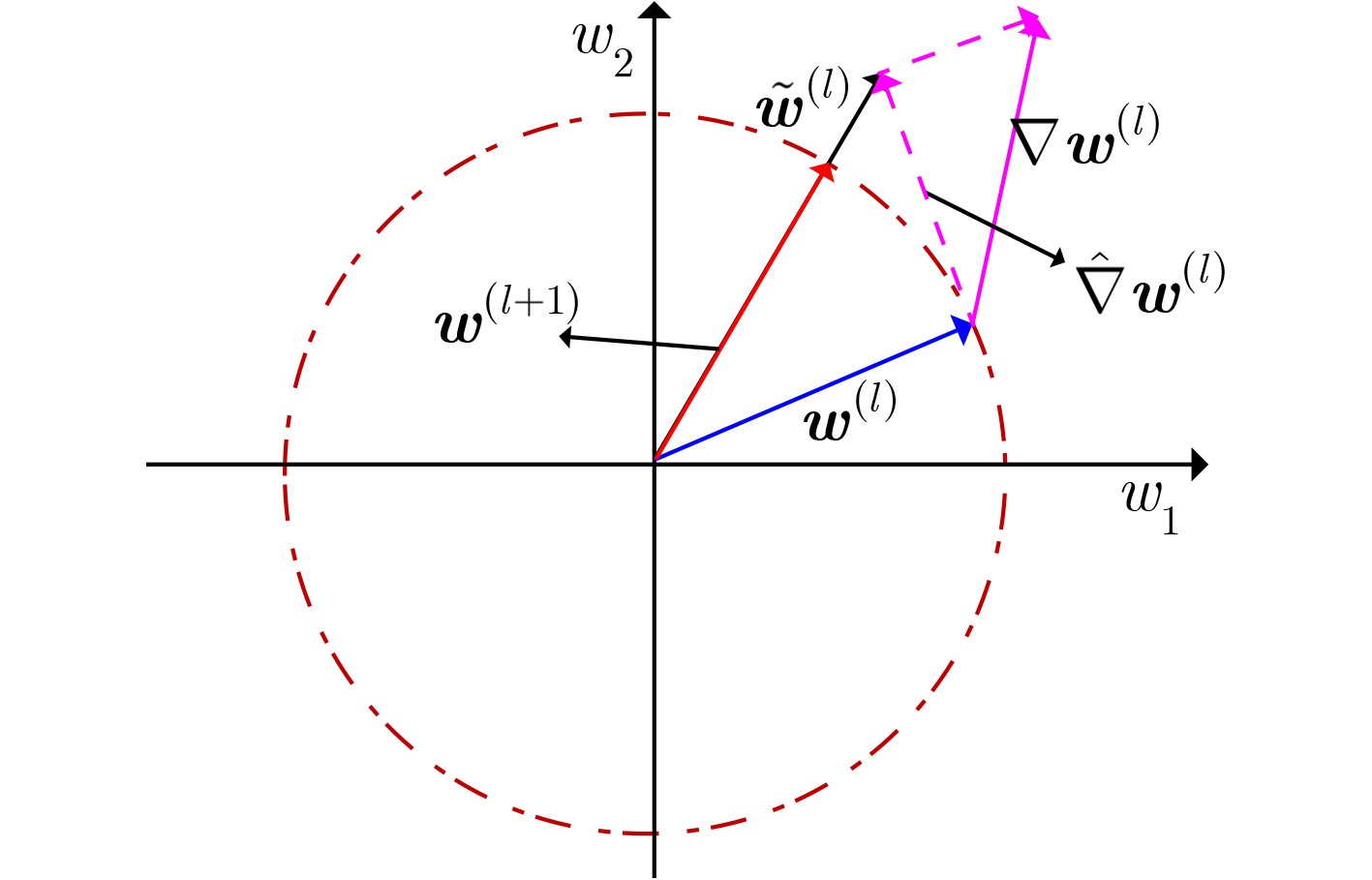
输入:发射阵元数目$ {M_{\text{T}}} $,正交基波形数目$ K $,加权系数${{\bar {\boldsymbol{w}}} }$,期望导向矢量${ {\tilde {\boldsymbol{A} } } } = [{ {\tilde {\boldsymbol{a} } } }_1^{\text{T} },{ {\tilde {\boldsymbol{a} } } }_2^{\text{T} },\cdots,{ {\tilde {\boldsymbol{a} } } }_N^{\text{T} }]$。 输出:最优发射加权矩阵(向量)$ {{\boldsymbol{w}}^ * } $。 初始化:$ {{\boldsymbol{w}}^{(l)}} $,且$ l = 0 $。 (1) 计算$ {\boldsymbol{P}} = {\boldsymbol{A\bar w}}{{\boldsymbol{A}}^{\text{H}}} $,$ {\boldsymbol{q}} = {\boldsymbol{A\bar w}}{{{\tilde {\boldsymbol{A}}}}^{\text{H}}} $,$ {{\tilde {\boldsymbol{A}}\bar {\boldsymbol{w}}}}{{{\tilde {\boldsymbol{A}}}}^{\text{H}}} $。 (2) 外循环操作: (a) 令$ l = l + 1 $; (b) 根据式(10)更新$ {\alpha ^{(l)}} $; (c) 令$ q = 0 $,$ {{\boldsymbol{w}}^{(l,q)}} = {{\boldsymbol{w}}^{(l - 1)}} $,计算参数$ {{\boldsymbol{\hat P}}^{(l)}} $; (d) 内循环操作: ① 根据式(13)计算$ {\nabla ^{(l,q)}} $; ② 根据式(15)计算$ {\hat \nabla ^{(l,q)}} $; ③ 根据式(16)更新$ {{{\tilde {\boldsymbol{w}}}}^{(l,q)}} $; ④ 根据式(17)进行缩放操作获得$ {{\boldsymbol{w}}^{(l,q + 1)}} $; ⑤ 令$ q = q + 1 $; ⑥ 判断是否满足收敛条件,如果是:内循环结束,令$ {{\boldsymbol{w}}^{(l)}} = {{\boldsymbol{w}}^{(l,q)}} $并转入步骤(e);如果否:转入步骤①。 (e) 判断是否满足收敛条件,如果是:外循环结束,转入步骤(3);如果否:转入步骤(a)。 (3) $ {{\boldsymbol{w}}^ * } = {{\boldsymbol{w}}^{(l)}} $。 -
[1] SHI Junpeng, WEN Fangqing, and LIU Tianpeng. Nested MIMO radar: Coarrays, tensor modeling, and angle estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(1): 573–585. doi: 10.1109/TAES.2020.3034012 [2] LAN Lan, MARINO A, AUBRY A, et al. GLRT-based adaptive target detection in FDA-MIMO radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(1): 597–613. doi: 10.1109/TAES.2020.3028485 [3] 朱莹, 张弓, 张劲东. 基于DCS的统计MIMO雷达信号模型及参数估计[J]. 雷达学报, 2012, 1(2): 143–148. doi: 10.3724/SP.J.1300.2012.20016ZHU Ying, ZHANG Gong, and ZHANG Jindong. Signal model and parameters estimation of statistical MIMO radar based on distributed compressed sensing[J]. Journal of Radars, 2012, 1(2): 143–148. doi: 10.3724/SP.J.1300.2012.20016 [4] ZHANG Haowei, SHI Junpeng, ZHANG Qiliang, et al. Antenna selection for target tracking in collocated MIMO radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(1): 423–436. doi: 10.1109/TAES.2020.3031767 [5] 陈晨, 张小飞, 李建峰. 波形相关矩阵未知情况下单基地MIMO雷达中一种改进MUSIC的DOA估计算法[J]. 电子与信息学报, 2012, 34(12): 2966–2971. doi: 10.3724/SP.J.1146.2012.00437CHEN Chen, ZHANG Xiaofei, and LI Jianfeng. An improved MUSIC DOA estimation algorithm for monostatic MIMO radar without knowledge of waveforms correlated matrix[J]. Journal of Electronics &Information Technology, 2012, 34(12): 2966–2971. doi: 10.3724/SP.J.1146.2012.00437 [6] 徐保庆, 赵永波, 庞晓娇. 基于实值处理的联合波束域双基地MIMO雷达测角算法[J]. 电子与信息学报, 2019, 41(7): 1721–1727. doi: 10.11999/JEIT180766XU Baoqing, ZHAO Yongbo, and PANG Xiaojiao. Joint real-valued beamspace-based method for angle estimation in bistatic MIMO radar[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1721–1727. doi: 10.11999/JEIT180766 [7] WU Kai, ZHANG J A, HUANG Xiaojing, et al. Waveform design and accurate channel estimation for frequency-hopping MIMO radar-based communications[J]. IEEE Transactions on Communications, 2021, 69(2): 1244–1258. doi: 10.1109/TCOMM.2020.3034357 [8] ZHANG Bo and DAI Fengzhou. Spatial-temporal waveform design for MIMO radar without approximating the covariance matrix[J]. IET Radar, Sonar & Navigation, 2020, 14(3): 381–387. doi: 10.1049/iet-rsn.2019.0395 [9] TANG Bo and LI Jian. Spectrally constrained MIMO radar waveform design based on mutual information[J]. IEEE Transactions on Signal Processing, 2019, 67(3): 821–834. doi: 10.1109/TSP.2018.2887186 [10] YU Xianxiang, CUI Guolong, YANG Jing, et al. MIMO radar transmit-receive design for moving target detection in signal-dependent clutter[J]. IEEE Transactions on Vehicular Technology, 2020, 69(1): 522–536. doi: 10.1109/TVT.2019.2951399 [11] SONG Junxiao, BABU P, and PALOMAR D P. Sequence set design with good correlation properties via majorization-minimization[J]. IEEE Transactions on Signal Processing, 2016, 64(11): 2866–2879. doi: 10.1109/TSP.2016.2535312 [12] CHENG Ziyang, HE Zishu, ZHANG Shengmiao, et al. Constant modulus waveform design for MIMO radar transmit beampattern[J]. IEEE Transactions on Signal Processing, 2017, 65(18): 4912–4923. doi: 10.1109/TSP.2017.2718976 [13] STOICA P, LI Jian, and XIE Yao. On probing signal design for MIMO radar[J]. IEEE Transactions on Signal Processing, 2007, 55(8): 4151–4161. doi: 10.1109/TSP.2007.894398 [14] STOICA P, LI Jian, and ZHU Xumin. Waveform synthesis for diversity-based transmit beampattern design[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2593–2598. doi: 10.1109/TSP.2007.916139 [15] HASSANIEN A and VOROBYOV S A. Transmit energy focusing for DOA estimation in MIMO radar with colocated antennas[J]. IEEE Transactions on Signal Processing, 2011, 59(6): 2669–2682. doi: 10.1109/TSP.2011.2125960 [16] KHABBAZIBASMENJ A, HASSANIEN A, VOROBYOV S A, et al. Efficient transmit beamspace design for search-free based DOA estimation in MIMO radar[J]. IEEE Transactions on Signal Processing, 2014, 62(6): 1490–1500. doi: 10.1109/TSP.2014.2299513 [17] 郑志东, 张剑云, 杨瑛. 基于发射波束域-平行因子分析的MIMO雷达收发角度估计[J]. 电子与信息学报, 2011, 33(12): 2875–2880. doi: 10.3724/SP.J.1146.2011.00440ZHENG Zhidong, ZHANG Jianyun, and YANG Ying. Joint DOD-DOA estimation of MIMO radar based on transmit beamspace-PARAFAC[J]. Journal of Electronics &Information Technology, 2011, 33(12): 2875–2880. doi: 10.3724/SP.J.1146.2011.00440 [18] 黄中瑞, 郑志东, 张剑云. 目标角度估计的多输入多输出雷达发射方向图综合[J]. 电波科学学报, 2015, 30(4): 789–796. doi: 10.13443/j.cjors.2014090401HUANG Zhongrui, ZHENG Zhidong, and ZHANG Jianyun. Transmit pattern synthesis of MIMO radar for the angle estimation[J]. Chinese Journal of Radio Science, 2015, 30(4): 789–796. doi: 10.13443/j.cjors.2014090401 [19] ALHUJAILI K, MONGA V, and RANGASWAMY M. Transmit MIMO radar beampattern design via optimization on the complex circle manifold[J]. IEEE Transactions on Signal Processing, 2019, 67(13): 3561–3575. doi: 10.1109/TSP.2019.2914884 -





 下载:
下载:


 下载:
下载:
