基于线性滤波器的四旋翼无人机强化学习控制策略

华和安; 方勇纯; 钱辰; 张雪涛

doi:10.11999/JEIT210251

基于线性滤波器的四旋翼无人机强化学习控制策略

doi: 10.11999/JEIT210251

1.
南开大学人工智能学院天津 300350
2.
大连理工大学智能机器人实验室大连 116024

基金项目: 国家自然科学基金(61873132, 61633012)

详细信息

作者简介:
华和安：男，1995年生，博士生，研究方向为旋翼无人机的智能控制与规划

方勇纯：男，1973年生，教授，研究方向为非线性控制、机器人视觉伺服、无人机和桥式吊车等欠驱动系统控制

钱辰：男，1993年生，博士生，研究方向为扑翼飞行器和其他仿生机器人的设计和控制

张雪涛：男，1992年生，副教授，研究方向为自主旋翼无人机的运动计划，视觉伺服，状态和干扰估计

通讯作者:
方勇纯　fangyc@nankai.edu.cn

中图分类号: V279; TP273
计量
- 文章访问数: 1291
- HTML全文浏览量: 1017
- PDF下载量: 164
- 被引次数: 0
出版历程
- 收稿日期: 2021-03-26
- 修回日期: 2021-10-20
- 网络出版日期: 2021-10-27
- 刊出日期: 2021-12-21

Reinforcement Learning Control Strategy of Quadrotor Unmanned Aerial Vehicles Based on Linear Filter

1.
College of Artificial Intelligence, Nankai University, Tianjin 300350, China
2.
Intelligent Robotic Laboratory, Dalian University of Technology, Dalian 116024, China

Funds: The National Natural Science Foundation of China (61873132, 61633012)

摘要

摘要: 针对四旋翼无人机(UAVs)系统，该文提出一种基于线性降阶滤波器的深度强化学习(RL)策略，进而设计了一种新型的智能控制方法，有效地提高了旋翼无人机对外界干扰和未建模动态的鲁棒性。首先，基于线性降阶滤波技术，设计了维数更少的滤波器变量作为深度网络的输入，减小了策略的探索空间，提高了策略的探索效率。在此基础上，为了增强策略对稳态误差的感知，该文结合滤波器变量和积分项，设计集总误差作为策略的新输入，提高了旋翼无人机的定位精度。该文的新颖之处在于，首次提出一种基于线性滤波器的深度强化学习策略，有效地消除了未知干扰和未建模动态对四旋翼无人机控制系统的影响，提高了系统的定位精度。对比实验结果表明，该方法能显著地提升旋翼无人机的定位精度和对干扰的鲁棒性。
- 四旋翼无人机 /
- 智能控制 /
- 强化学习 /
- 未知干扰
Abstract: In this paper, based on linear filter, a deep Reinforcement Learning (RL) strategy is proposed, then a novel intelligent control method is put forward for quadrotor Unmanned Aerial Vehicles (UAVs), which improves effectively the robustness against disturbance and unmodeled dynamics. First of all, based on linear reduced-order filtering technology, filter variables with fewer dimensions are designed as the input of the deep network, which reduces the exploration space of the strategy and improves the exploration efficiency. On this basis, to enhance strategy perception of steady-state errors, the filter variables and integration terms are combined to design the lumped error as the new network input, which improves the positioning accuracy of quadrotor UAVs. The novelty of this paper lies in that it is the first intelligent approach based on linear filtering technology, to eliminate successfully the influence of unknown disturbance and unmodeled dynamics of quadrotor UAVs, which improves the positioning accuracy. The results of comparative experiments show the effectiveness of the proposed method in terms of improving positioning accuracy and enhancing robustness.
- Quadrotor Unmanned Aerial Vehicles (UAVs) /
- Intelligent control /
- Reinforcement Learning(RL) /
- Unknown disturbance

HTML全文

图 1 强化学习策略和旋翼无人机的交互

下载: 全尺寸图片幻灯片

图 2 四旋翼无人机控制策略学习过程示意图

下载: 全尺寸图片幻灯片

图 3 5种学习方法的训练结果及测试2曲线图

下载: 全尺寸图片幻灯片

图 4 测试3和测试4结果曲线图

下载: 全尺寸图片幻灯片

图 5 实验平台

下载: 全尺寸图片幻灯片

表 1 强化学习训练-评价算法

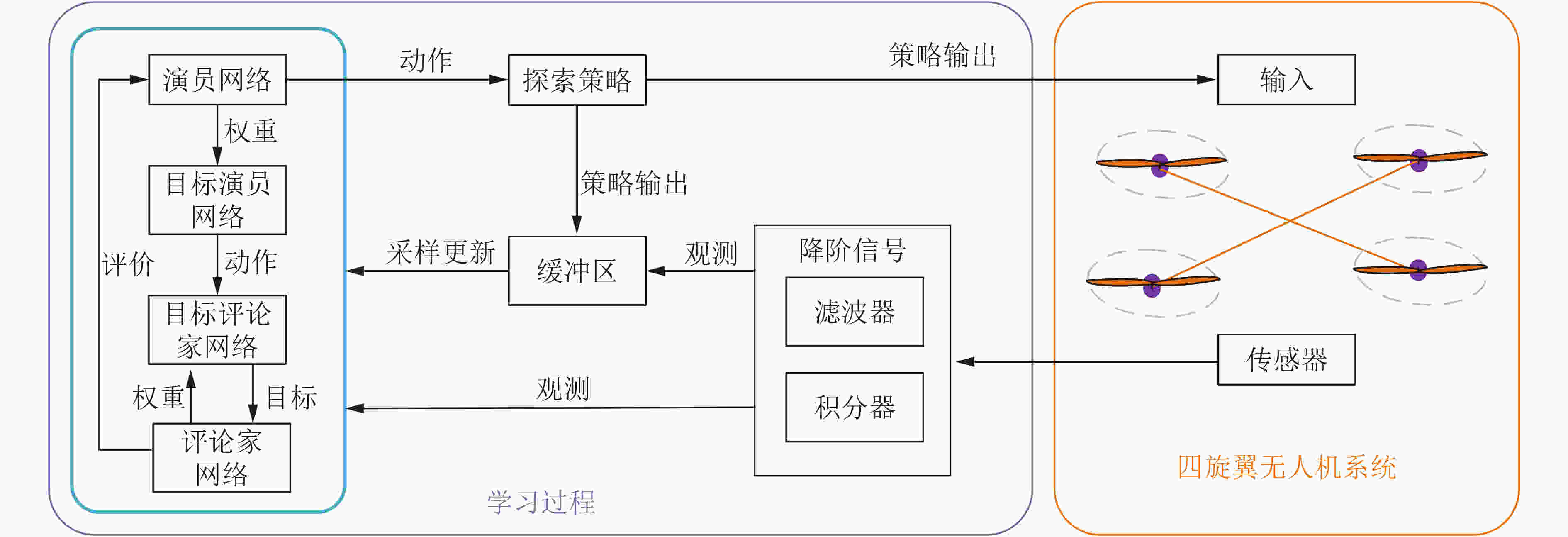
随机初始化评论家和演员并且以相同的参数初始化对应的目标网络
初始化回放缓冲区
for i = 1 to 500 do
随机初始化无人机位置，观测初始状态
for j = 1 to 500 do
根据控制器式(10)生成控制信号作用于无人机
观测奖励值和下一状态
将当前的交互数据保存在回放缓冲区中
随机从缓冲区采样一组数据
根据式(8)和式(9)更新评论家和演员网络
根据式(6)更新目标网络
if j = 500 do
for k = 1 to 200 do
测试当前策略
end for
end if
end for
end for

下载: 导出CSV

表 2 系统的参数

参数	值	参数	值
$m$	$1.6{\text{ kg}}$	${k_i},i = x,y,z$	$ 0.1,{\text{ }}0.1,{\text{ }}0.1 $
${\boldsymbol{J}}$	${\text{diag}}[0.01,0.01,0.02]{\text{ kg}} \cdot {{\text{m}}^{\text{2}}}$	${{\boldsymbol{K}}_1}$	${\text{diag}}[3.8,3.8,3.5]{\text{ }}$
$\tau $	$ 0.001 $	${{\boldsymbol{K}}_2}$	${\text{diag}}[5.0,5.0,4.5]{\text{ }}$
$g$	$9.8{\text{ m/}}{{\text{s}}^{\text{2}}}$	$\mathcal{B}$	$10000$
$\boldsymbol{\sigma }$	$ \left[ {0.1,0.1,1.0} \right] $	$\gamma $	$0.95$
$ {\beta _i},i = x,y,z $	$ 0.1,{\text{ }}0.1,{\text{ }}0.1 $	$N$	$64$
${\alpha _\omega }$	$0.0001$	$ {\alpha _\mu } $	$0.0001$

下载: 导出CSV

表 3 测试2：最大稳态误差和均方根误差

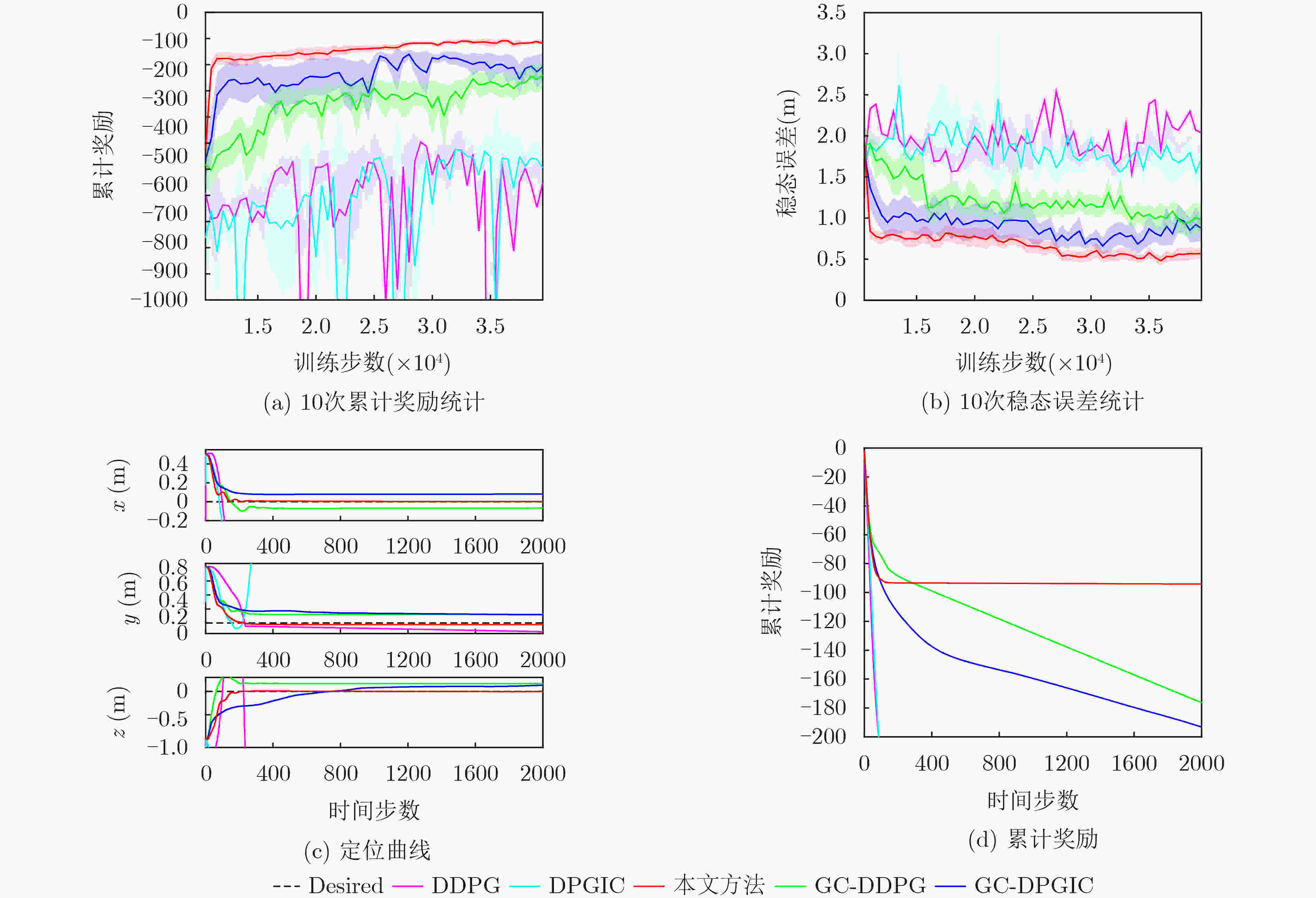
方法	X轴(m)		Y轴(m)		Z轴(m)
方法	MSSE	RMSE	MSSE	RMSE	MSSE	RMSE
本文算法	0.0075	0.0035	0.0216	0.0212	0.0078	0.0034
DDPG	1.4904	1.3661	0.1140	0.0821	1.4002	1.4001
DPGIC	2.2356	2.0656	1.7060	1.6571	1.4003	1.3998
GC-DDPG	0.0716	0.0698	0.1297	0.1227	0.1740	0.1689
GC-DPGIC	0.0803	0.0788	0.1757	0.1439	0.2910	0.1114

下载: 导出CSV

表 4 测试3：最大稳态误差和均方根误差

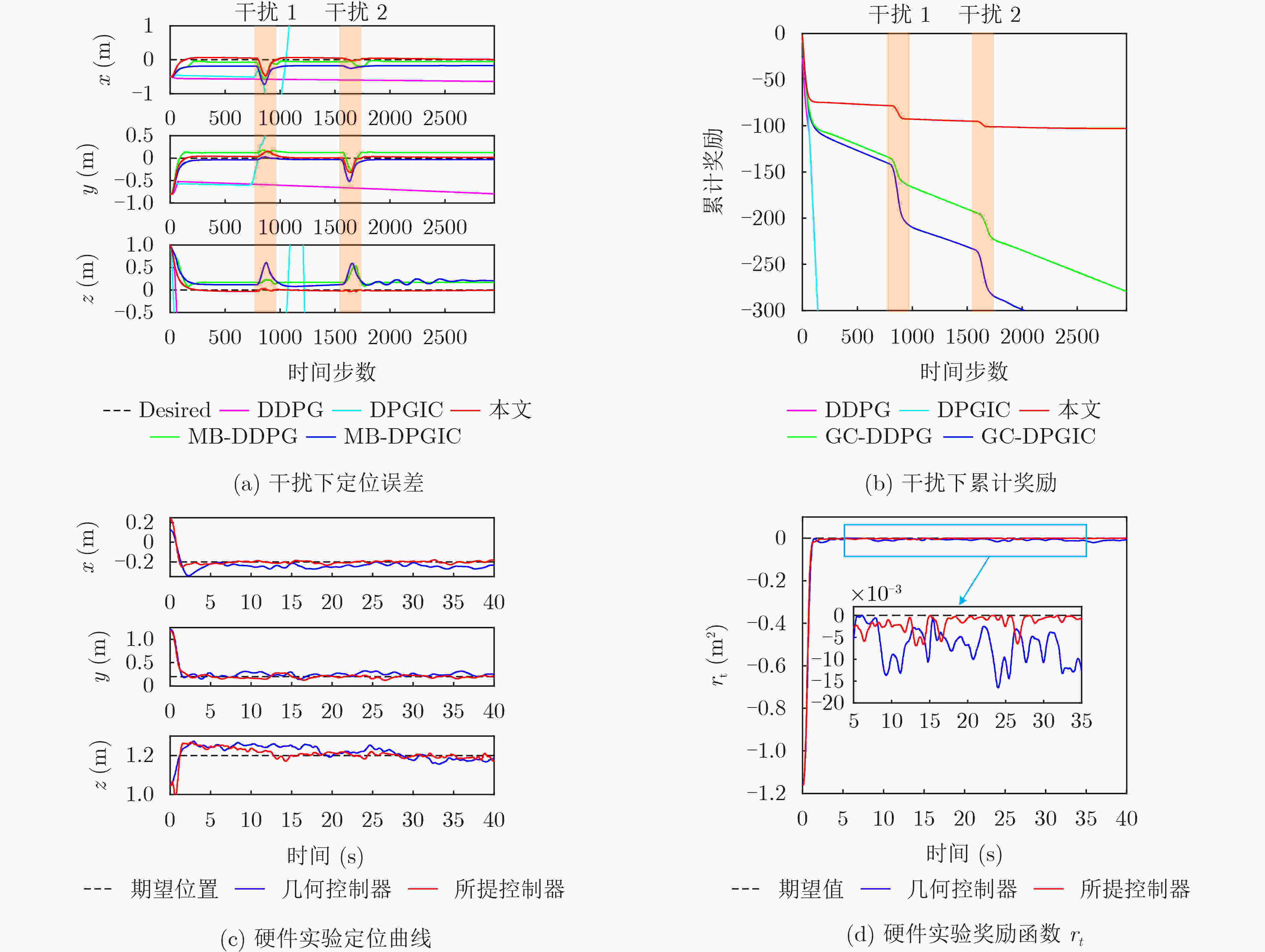
方法	X轴(m)		Y轴(m)		Z轴 (m)
方法	MSSE	RMSE	MSSE	RMSE	MSSE	RMSE
本文算法	0.4715	0.0887	0.3207	0.0647	0.0356	0.0203
DDPG	0.6239	0.5904	0.7480	0.6440	1.4002	1.4001
DPGIC	56.45	41.68	15.26	11.80	3.792	1.497
GC-DDPG	0.5543	0.1170	0.2918	0.1320	0.5382	0.1896
GC-DPGIC	0.7250	0.2228	0.5186	0.0912	0.6081	0.2014

下载: 导出CSV

表 5 测试4：最大稳态误差和均方根误差

方法	X轴(m)		Y轴(m)		Z轴(m)
方法	MSSE	RMSE	MSSE	RMSE	MSSE	RMSE
几何控制器	0.0730	0.0437	0.1221	0.0595	0.0670	0.0371
所提控制器	0.0340	0.0117	0.0802	0.0348	0.0535	0.0203

下载: 导出CSV

参考文献(27)

[1]	张坤, 高晓光. 未知风场扰动下无人机三维航迹跟踪鲁棒最优控制[J]. 电子与信息学报, 2015, 37(12): 3009–3015. ZHANG Kun and GAO Xiaoguang. Robust optimal control for unmanned aerial vehicles’ three-dimensional trajectory tracking in wind disturbance[J]. Journal of Electronics &Information Technology, 2015, 37(12): 3009–3015.
[2]	宋大雷, 齐俊桐, 韩建达, 等. 旋翼飞行机器人系统建模与主动模型控制理论及实验研究[J]. 自动化学报, 2011, 37(4): 480–495. doi: 10.3724/SP.J.1004.2011.00480 SONG Dalei, QI Juntong, HAN Jianda, et al. Model identification and active modeling control for rotor fly-robot: Theory and experiment[J]. Acta Automatica Sinica, 2011, 37(4): 480–495. doi: 10.3724/SP.J.1004.2011.00480
[3]	孟祥冬, 何玉庆, 韩建达. 接触作业型飞行机械臂系统的力/位置混合控制[J]. 机器人, 2020, 42(2): 167–178. MENG Xiangdong, HE Yuqing, and HAN Jianda. Hybrid force/position control of aerial manipulators in contact operation[J]. Robot, 2020, 42(2): 167–178.
[4]	王诗章, 鲜斌, 杨森. 无人机吊挂飞行系统的减摆控制设计[J]. 自动化学报, 2018, 44(10): 1771–1780. WANG Shizhang, XIAN Bin, and YANG Sen. Anti-swing controller design for an unmanned aerial vehicle with a slung-load[J]. Acta Automatica Sinica, 2018, 44(10): 1771–1780.
[5]	甄子洋. 舰载无人机自主着舰回收制导与控制研究进展[J]. 自动化学报, 2019, 45(4): 669–681. ZHEN Ziyang. Research development in autonomous carrier-landing/ship-recovery guidance and control of unmanned aerial vehicles[J]. Acta Automatica Sinica, 2019, 45(4): 669–681.
[6]	赵太飞, 宫春杰, 张港, 等. 一种无人机集群安全高效的分区集结控制策略[J]. 电子与信息学报, 2021, 43(8): 2181–2188. doi: 10.11999/JEIT200601 ZHAO Taifei, GONG Chunjie, ZHANG Gang, et al. A safe and high efficiency control strategy of unmanned aerial vehicles partition rendezvous[J]. Journal of Electronics and Information Technology, 2021, 43(8): 2181–2188. doi: 10.11999/JEIT200601
[7]	李瑞涵, 王耀南, 谭建豪. Nesterov加速梯度无人机姿态融合算法[J]. 机器人, 2018, 40(6): 852–859. LI Ruihan, WANG Yaonan, and TAN Jianhao. Attitude fusion algorithm of UAV based on Nesterov accelerated gradient[J]. Robot, 2018, 40(6): 852–859.
[8]	高杨, 李东生, 程泽新. 无人机分布式集群态势感知模型研究[J]. 电子与信息学报, 2018, 40(6): 1271–1278. doi: 10.11999/JEIT170877 GAO Yang, LI Dongsheng, and CHENG Zexin. UAV distributed swarm situation awareness model[J]. Journal of Electronics &Information Technology, 2018, 40(6): 1271–1278. doi: 10.11999/JEIT170877
[9]	ZHENG Dongliang, WANG Hesheng, WANG Jingchuan, et al. Toward visibility guaranteed visual servoing control of quadrotor UAVs[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(3): 1087–1095. doi: 10.1109/TMECH.2019.2906430
[10]	ZHANG Xuetao, FANG Yongchun, ZHANG Xuebao, et al. A novel geometric hierarchical approach for dynamic visual servoing of quadrotors[J]. IEEE Transactions on Industrial Electronics, 2020, 67(5): 3840–3849. doi: 10.1109/TIE.2019.2917420
[11]	MAHONY R and HAMEL T. Image-based visual servo control of aerial robotic systems using linear image features[J]. IEEE Transactions on Robotics, 2005, 21(2): 227–239. doi: 10.1109/TRO.2004.835446
[12]	LIU Hao, ZHAO Wanbin, ZUO Zongyu, et al. Robust control for quadrotors with multiple time-varying uncertainties and delays[J]. IEEE Transactions on Industrial Electronics, 2017, 64(2): 1303–1312. doi: 10.1109/TIE.2016.2612618
[13]	HUA He’an, FANG Yongchun, ZHANG Xuetao, et al. Auto-tuning nonlinear PID-type controller for rotorcraft-based aggressive transportation[J]. Mechanical Systems and Signal Processing, 2020, 145: 106858. doi: 10.1016/j.ymssp.2020.106858
[14]	ZUO Zongyu and MALLIKARJUNAN S. L₁ adaptive backstepping for robust trajectory tracking of UAVs[J]. IEEE Transactions on Industrial Electronics, 2017, 64(4): 2944–2954. doi: 10.1109/TIE.2016.2632682
[15]	LV Zongyang, LI Shengming, WU Yuhu, et al. Adaptive control for a quadrotor transporting a cable-suspended payload with unknown mass in the presence of rotor downwash[J]. IEEE Transactions on Vehicular Technology, 2021, 70(9): 8505–8518. doi: 10.1109/TVT.2021.3096234
[16]	TIAN Bailing, YIN Liping, and WANG Hong. Finite-time reentry attitude control based on adaptive multivariable disturbance compensation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5889–5898. doi: 10.1109/TIE.2015.2442224
[17]	XIAN Bin and HAO Wei. Nonlinear robust fault-tolerant control of the tilt trirotor UAV under rear servo's stuck fault: Theory and experiments[J]. IEEE Transactions on Industrial Informatics, 2019, 15(4): 2158–2166. doi: 10.1109/TII.2018.2858143
[18]	SHI Haobin, LI Xuesi, HWANG K S, et al. Decoupled visual servoing with fuzzy Q-learning[J]. IEEE Transactions on Industrial Informatics, 2018, 14(1): 241–252. doi: 10.1109/TII.2016.2617464
[19]	HWANGBO J, SA I, SIEGWART R, et al. Control of a quadrotor with reinforcement learning[J]. IEEE Robotics and Automation Letters, 2017, 2(4): 2096–2103. doi: 10.1109/LRA.2017.2720851
[20]	MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529–533. doi: 10.1038/nature14236
[21]	SILVER D, LEVER G, HEESS N, et al. Deterministic policy gradient algorithms[C]. The 31st International Conference on Machine Learning, Beijing, China, 2014: 387–395.
[22]	LILLICRAP T P, HUNT J J, PRITZEL A, et al. Continuous control with deep reinforcement learning[C]. Proceedings of the 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2016: 1–14.
[23]	RODRIGUEZ-RAMOS A, SAMPEDRO C, BAVLE H, et al. A deep reinforcement learning strategy for UAV autonomous landing on a moving platform[J]. Journal of Intelligent & Robotic Systems, 2019, 93(1/2): 351–366.
[24]	WANG Yuanda, SUN Jia, HE Haibo, et al. Deterministic policy gradient with integral compensator for robust quadrotor control[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2020, 50(10): 3713–3725. doi: 10.1109/TSMC.2018.2884725
[25]	WEI Qinglai, WANG Lingxiao, LIU Yu, et al. Optimal elevator group control via deep asynchronous actor-critic learning[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(12): 5245–5256. doi: 10.1109/TNNLS.2020.2965208
[26]	LEE T, LEOK M, and MCCLAMROCH N H. Geometric tracking control of a quadrotor UAV on SE(3)[C]. The 49th IEEE Conference on Decision and Control, Atlanta, USA, 2010: 5420–5425.
[27]	FURRER F, BURRI M, ACHTELIK M, et al. RotorS-a Modular Gazebo MAV Simulator Framework[M]. KOUBAA A. Robot Operating System (ROS): The Complete Reference (Volume 1). Cham: Springer, 2016: 595–625.