Cost-reference Particle Filter Bank Based Track-before-detecting Algorithm
-
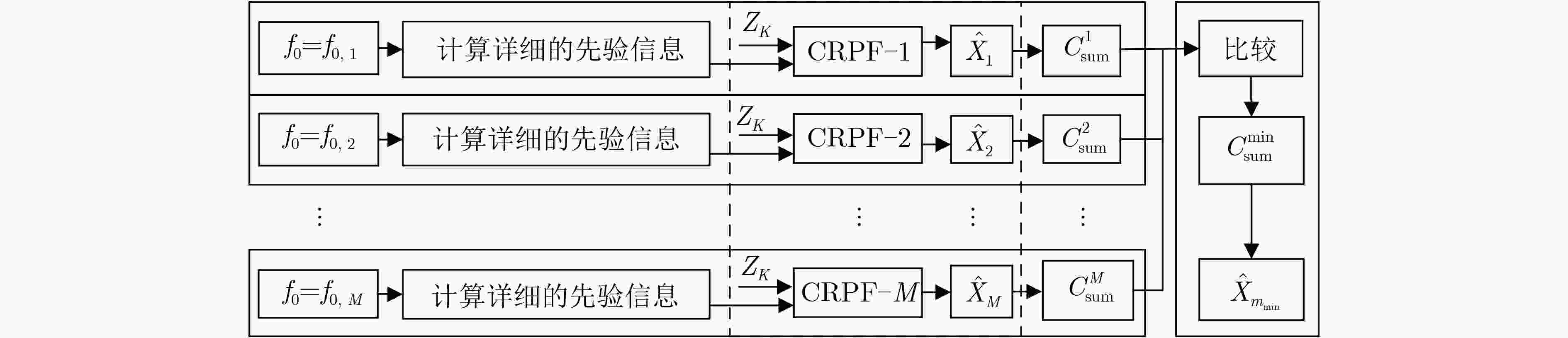
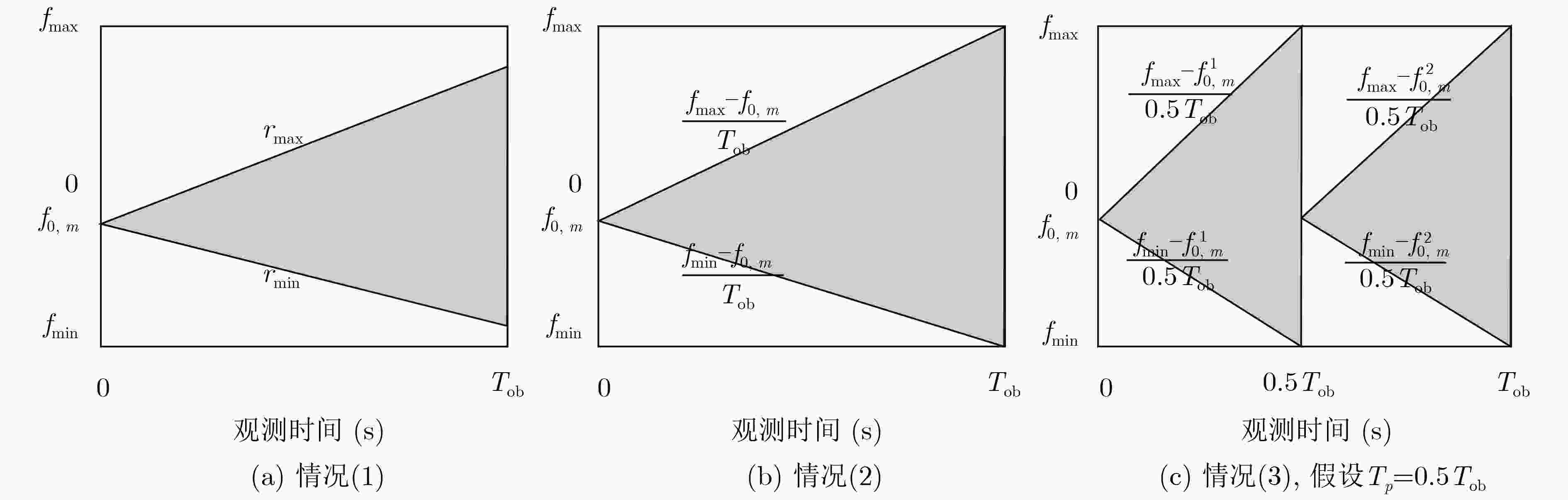
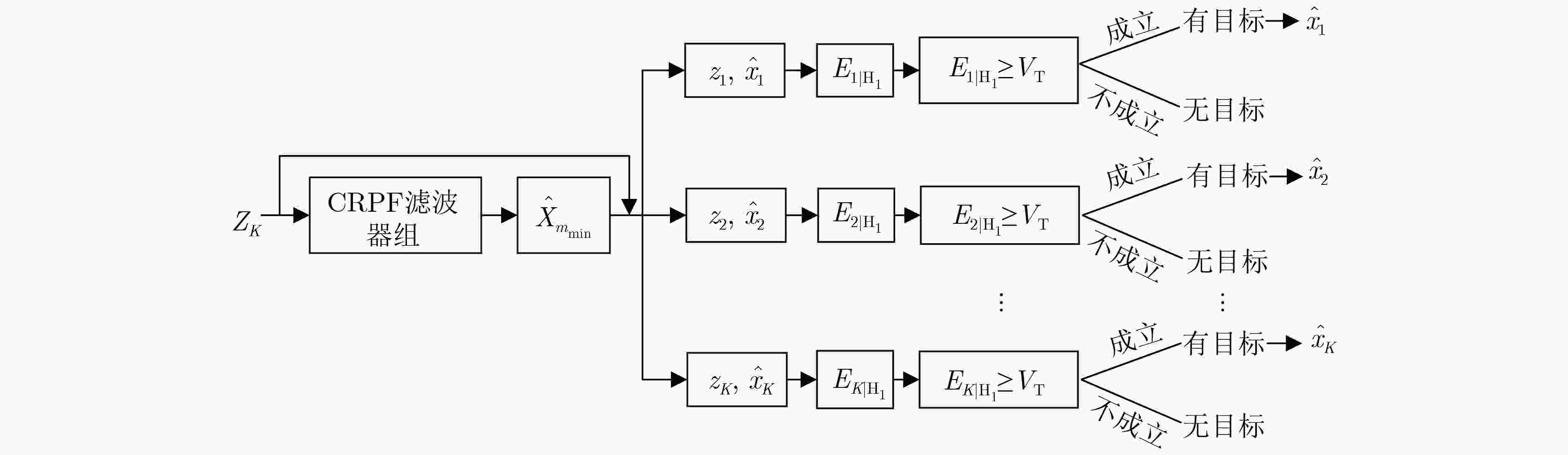
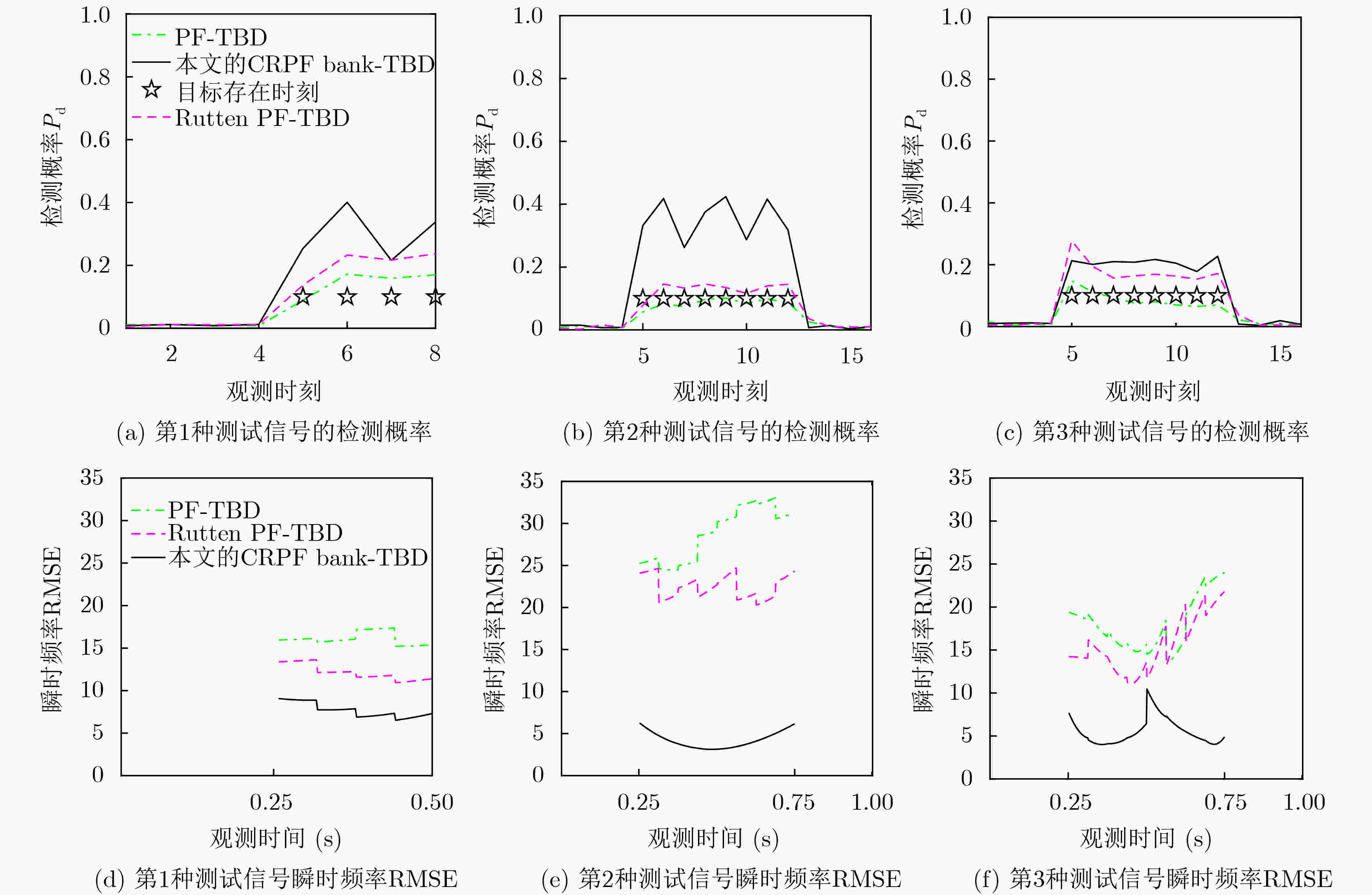
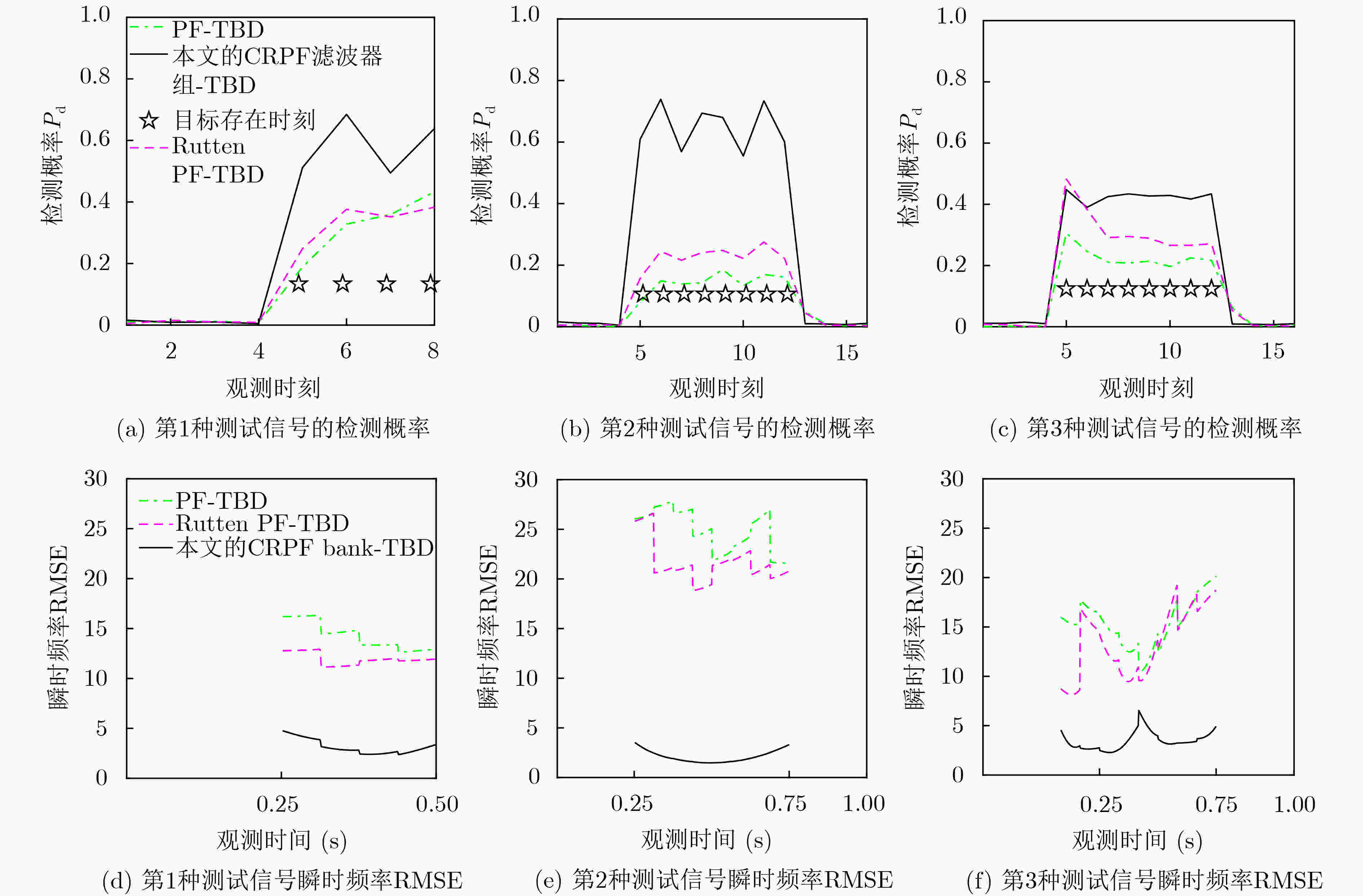
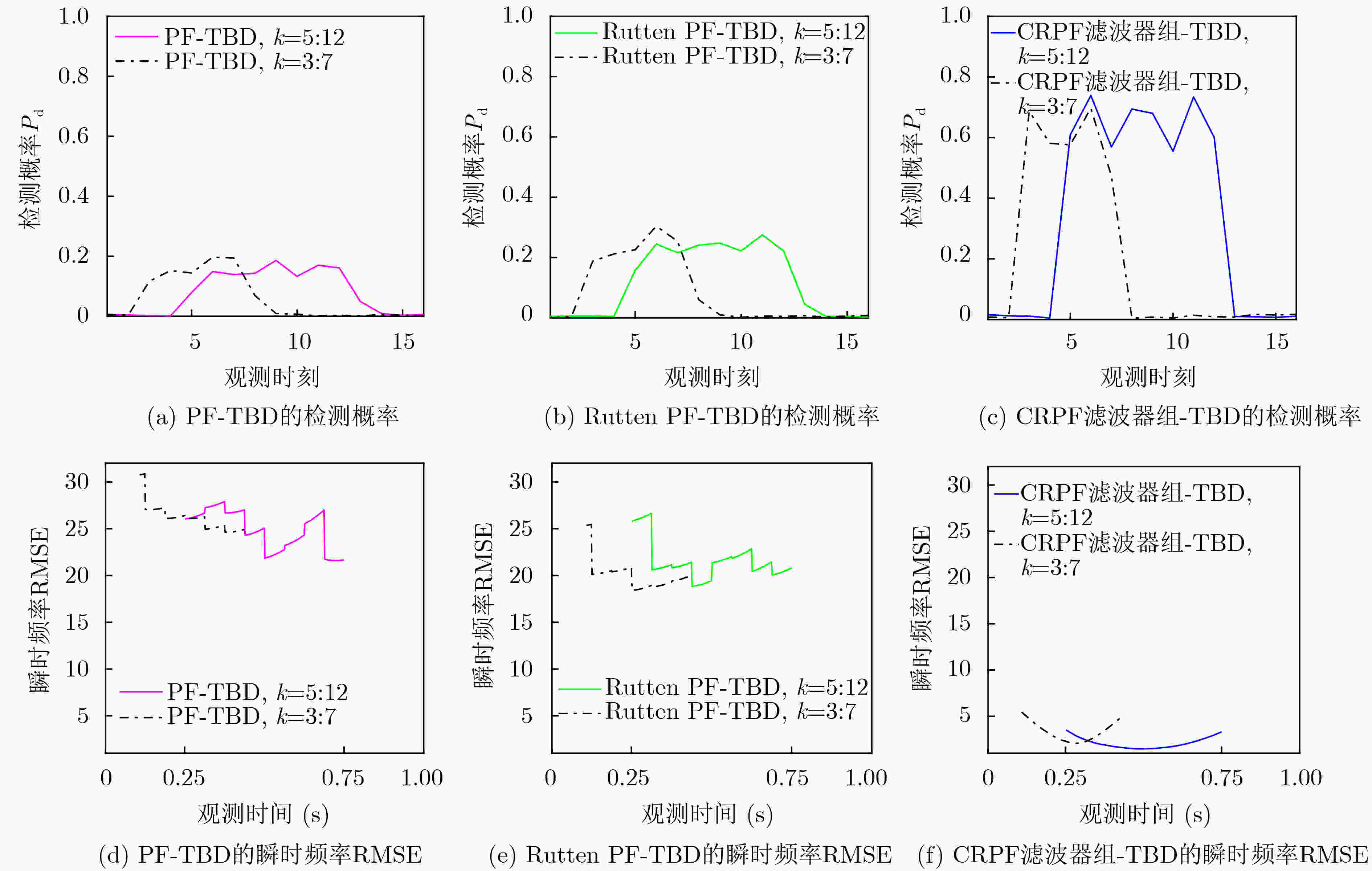
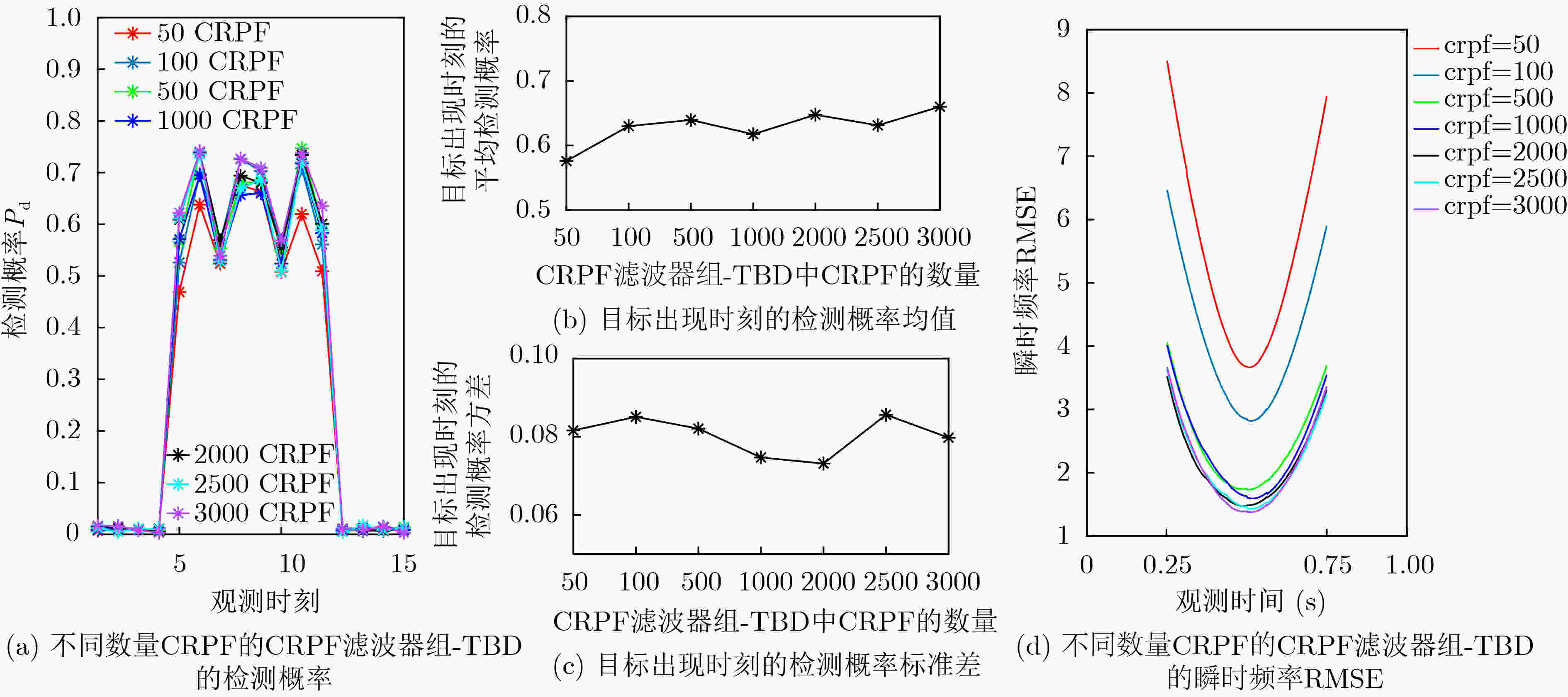
摘要: 基于粒子滤波的检测前跟踪方法是检测和估计非线性调频信号的有效方法之一。但此类方法运算量大,难以并行执行。此外,由于粒子滤波算法收敛较慢,基于粒子滤波的检测前跟踪方法的检测和状态估计能力有待提高。针对上述问题,该文首先提出一种代价参考粒子滤波器组。该滤波器组收敛快速,具有完全的并行结构,可快速准确地估计非线性调频信号的瞬时频率。其次,提出基于代价参考滤波器组的检测前跟踪算法,可在给定虚警率下,在各个时刻检测目标和估计目标状态。两类非线性调频信号检测和估计的仿真结果表明,基于代价参考粒子滤波器组的检测前跟踪算法的检测性能、估计性能和运行速率均优于类似的方法,如基于粒子滤波的检测前跟踪方法,基于Rutten粒子滤波的检测前跟踪方法等。Abstract: Detection and tracking of low signal-to-noise ratio nonlinear frequency modulated signal can be effectively solved by Track-Before-Detecting (TBD) algorithms based on particle filters. However, the algorithms are high in computational complexity and hard to be implemented in parallel. Furthermore, because of the comparatively long convergence processing, the detection and state estimation capabilities of the particle filters based methods are limited. In this paper, a cost-reference particle filter bank is proposed, which does not depend on the distribution of the system and has an entirely parallel structure. Then a detection method based on the cost-reference particle filter bank is proposed. Simulation results of two nonlinear frequency modulated signals detection and estimation illustrate that the propose method has better performance in detection, estimation, and running speed than similar methods, such as particle filter based track-before-detecting algorithm, Rutten particle filter based TBD algorithm.
-
表 1 本文的CRPF滤波器组-TBD与PF-TBD, Rutten PF-TBD的运行时间(s)比较
PF-TBD(×10–1) Rutten PF-TBD(×10–1) CRPF滤波器组-TBD(×10–4) 第1种测试信号 1.135 2.535 1.058 第2种测试信号 3.125 5.218 2.180 第3种测试信号 3.352 5.244 2.128 -
[1] ZHOU Gongjian, WANG Liangliang, and KIRUBARAJAN T. A pseudo-spectrum approach for weak target detection and tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(6): 3394–3412. doi: 10.1109/TAES.2019.2906419 [2] TU Xiaotong, HU Yue, LI Fucai, et al. Instantaneous frequency estimation for nonlinear FM signal based on modified polynomial chirplet transform[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(11): 2898–2908. doi: 10.1109/TIM.2017.2730982 [3] WANG Wei, WANG R, ZHANG Zhimin, et al. First demonstration of airborne SAR with nonlinear FM chirp waveforms[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(2): 247–251. doi: 10.1109/LGRS.2015.2508102 [4] LIU Jiafang, ZHANG Yunhua, and DONG Xiao. Dechirping compression method for nonlinear frequency modulation waveforms[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(3): 377–381. doi: 10.1109/LGRS.2018.2875893 [5] SHUI Penglang, BAO Zheng, and SU Hongtao. Nonparametric detection of FM signals using time-frequency ridge energy[J]. IEEE Transactions on Signal Processing, 2008, 56(5): 1749–1760. doi: 10.1109/tsp.2007.909322 [6] CANDÈS E J, CHARLTON P R, and HELGASON H. Detecting highly oscillatory signals by chirplet path pursuit[J]. Applied and Computational Harmonic Analysis, 2008, 24(1): 14–40. doi: 10.1016/j.acha.2007.04.003 [7] SALMOND D J and BIRCH H. A particle filter for track-before-detect[C]. 2001 American Control Conference. (Cat. No. 01CH37148), Arlington, USA, 2001: 3755–3760. doi: 10.1109/acc.2001.946220 [8] LU Jin, SHUI Penglang, and SU Hongtao. Track-before-detect method based on cost-reference particle filter in non-linear dynamic systems with unknown statistics[J]. IET Signal Processing, 2014, 8(1): 85–94. doi: 10.1049/iet-spr.2013.0117 [9] SHUI Penglang, SHI Sainan, LU Jin, et al. Detection of nonlinear FM signals via forward-backward cost-reference particle filter[J]. Digital Signal Processing, 2016, 48: 104–115. doi: 10.1016/j.dsp.2015.09.016 [10] RISTIC B, ARULAMPALM S, and GORDON N. Beyond the Kalman Filter: Particle Filters for Tracking Applications[M]. Boston: Artech House, 2004: 239–258. [11] RUTTEN M G, RISTIC B, and GORDON N J. A comparison of particle filters for recursive track-before-detect[C]. The 7th International Conference on Information Fusion, Philadelphia, USA, 2005: 169–175. doi: 10.1109/ICIF.2005.1591851. [12] YI Wei, FU Lingzhi, GARCÍA-FERNÁNDEZ Á F, et al. Particle filtering based track-before-detect method for passive array sonar systems[J]. Signal Processing, 2019, 165: 303–314. doi: 10.1016/j.sigpro.2019.07.027 [13] ZHANG Tianzhu, XU Changsheng, and YANG M H. Learning multi-task correlation particle filters for visual tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(2): 365–378. doi: 10.1109/TPAMI.2018.2797062 [14] VITETTA G M, SIRIGNANO E, DI VIESTI P, et al. Marginalized particle filtering and related filtering techniques as message passing[J]. IEEE Transactions on Signal Processing, 2019, 67(6): 1522–1536. doi: 10.1109/TSP.2019.2893868 [15] CHEN Hanxin, FAN Dongliang, FANG Lu, et al. Particle swarm optimization algorithm with mutation operator for particle filter noise reduction in mechanical fault diagnosis[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2020, 34(10): 2058012. doi: 10.1142/S0218001420580124 [16] ZENG Nianyin, WANG Zidong, ZHANG Hong, et al. An improved particle filter with a novel hybrid proposal distribution for quantitative analysis of gold immunochromatographic strips[J]. IEEE Transactions on Nanotechnology, 2019, 18: 819–829. doi: 10.1109/TNANO.2019.2932271 [17] MÍGUEZ J, BUGALLO M F, and DJURIĆ P M. A new class of particle filters for random dynamic systems with unknown statistics[J]. EURASIP Journal on Advances in Signal Processing, 2004, 2004(15): 303619. doi: 10.1155/S1110865704406039 [18] MÍGUEZ J. Analysis of parallelizable resampling algorithms for particle filtering[J]. Signal Processing, 2007, 87(12): 3155–3174. doi: 10.1016/j.sigpro.2007.06.011 [19] NOVEY M, ADALI T, and ROY A. Correspondence: A complex generalized Gaussian distribution-characterization, generation, and estimation[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1427–1433. doi: 10.1109/TSP.2009.2036049 -





 下载:
下载:



 下载:
下载:
