Design of Four-bit Subtracter Using Excess-3 Code Rules Based on DNA Domain Coding
-
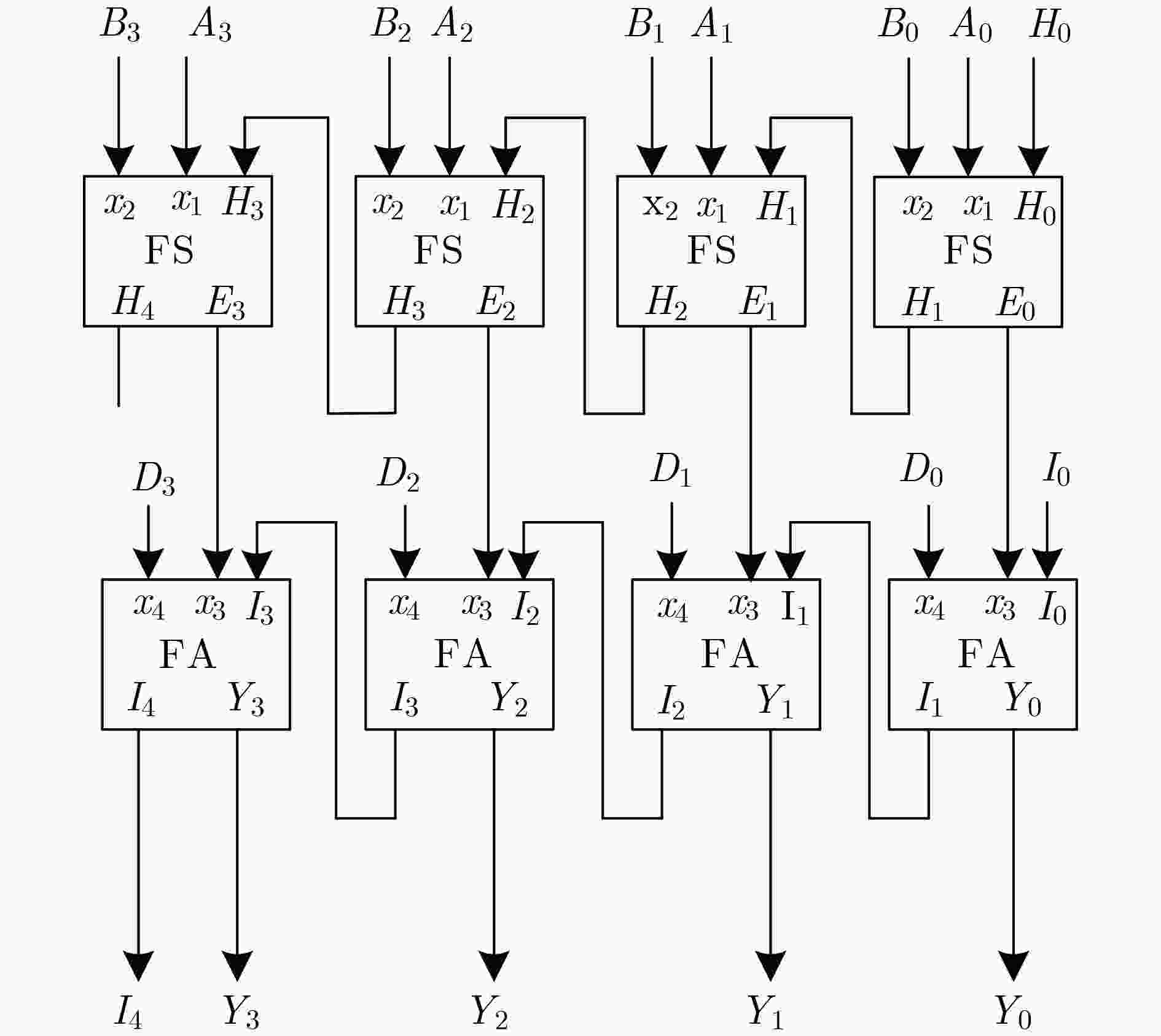
摘要: DNA分子逻辑电路的设计是DNA计算领域的重要研究方向。该文针对当前双轨分子逻辑电路复杂度高、响应时间慢的问题,提出一种基于域编码策略的DNA逻辑电路设计的新方法。该文设计了“多输入1输出”逻辑运算模块,构建了扇出门和放大器,并利用所构建的电路模块搭建了4位平方根分子逻辑电路,与经典的双轨策略下的4位平方根电路相比,反应物的数量由双轨的130种降低为61种,系统响应时间缩减为双轨的1/24,大大简化了电路的复杂度,提高了系统的响应速度,进一步验证了域编码策略在分子逻辑电路设计中的有效性。为了深度解析基于域编码策略的大规模复杂分子逻辑电路的设计思想,该文构造了“余三码四位减法器”,为设计大规模功能性DNA逻辑电路提供了更多的解决方案。Abstract: The design of DNA molecular logic circuits is an important direction in the field of DNA computing. Considering the problems of high complexity and slow response time for dual rail molecular logic circuits, a new strategy based on DNA domain coding is proposed in this study, which is used to construct molecular logic circuits. In this paper, the operation modules of “multiple-inputs-one-output” are introduced, and the fan-out gates and amplification gates are also constructed. Then, the molecular logic circuit to solve four-bits-square-rooting is formed with these logic computing modules designed in this paper. Compared with the four-bit square root circuit under the classical dual-track strategy, the number of reactants is reduced from 130 to 61, and the system response time is reduced to 1 / 24 of the dual-track strategy, which simplifies greatly the complexity of the circuit and improves the response speed of the system. It verifies further the effectiveness of the domain coding strategy in the design of molecular logic circuits. In order to analyze further the design concept for large-scale complicated molecular logic circuits based on domain coding, a four-bit excess-3 code subtracter is constructed, which provides more solutions for designing large-scale functional DNA logic circuits.
-
Key words:
- Domain coding /
- DNA strand displacement /
- Dual rail /
- Excess-3 code /
- Subtracter
-
表 1 DNA信号链及逻辑值
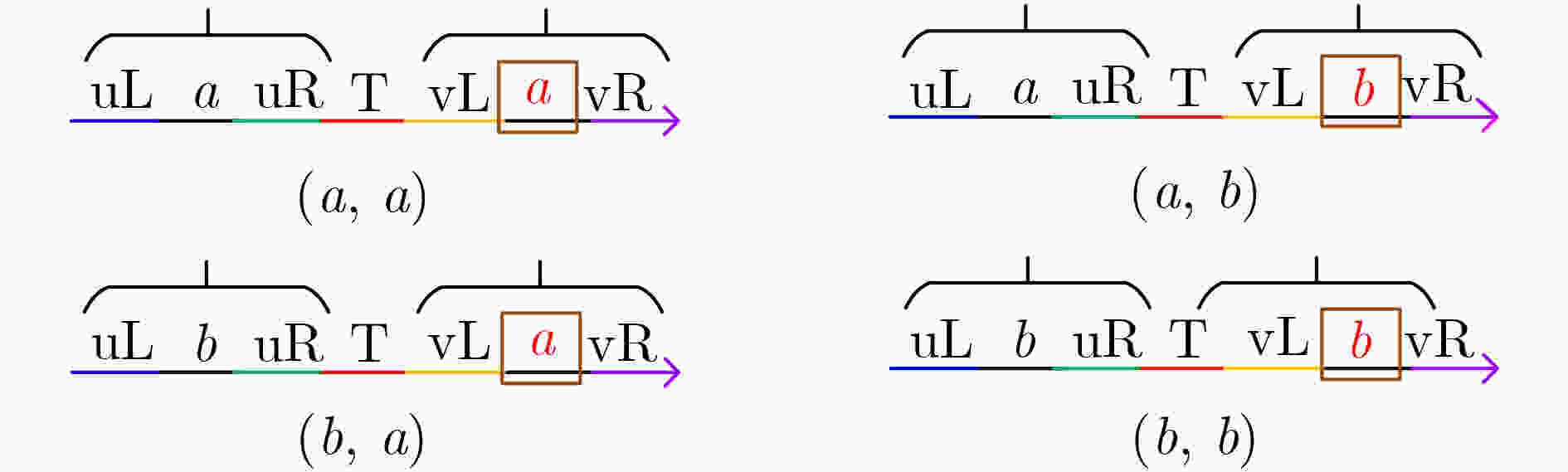
DNA信号链 输入/输出 逻辑值 <j1L^ b j1R^ T^ u1L^ a u1R^> A0 0 <j3L^ b j3R^ T^ u3L^ a u3R^> A1 0 <j5L^ b j5R^ T^ u5L^ a u5R^> A2 0 <j7L^ b j7R^ T^ u7L^ b u7R^> A3 1 <j2L^ b j2R^ T^ u2L^ b u2R^> B0 1 <j4L^ b j4R^ T^ u4L^ a u4R^> B1 0 <j6L^ b j6R^ T^ u6L^ b u6R^> B2 1 <j8L^ b j8R^ T^ u8L^ a u8R^> B3 0 <j0L^ b j0R^ T^ u0L^ a u0R^> H0 0 <j9L^ b j9R^ T^ u9L^ a u9R^> I0 0 <j10L^ b j10R^ T^ u10L^ b u10R^> D0 1 <j11L^ b j11R^ T^ u11L^ b u11R^> D1 1 <j12L^ b j12R^ T^ u12L^ a u12R^> D2 0 <j13L^ b j13R^ T^ u13L^ a u13R^> D3 0 <wL^ a wR^ fluor01> Y00 0 <pL^ b pR^ fluor12> Y11 1 <qL^ b qR^ fluor22> Y21 1 <mL^ a mR^ fluor31> Y30 0 <nL^ a nR^ fluor33> I40 0 -
[1] LLOYD S. Ultimate physical limits to computation[J]. Nature, 2000, 406(6799): 1047–1054. doi: 10.1038/35023282 [2] 杨姗, 李金玉, 崔玉军, 等. DNA计算的发展现状及未来展望[J]. 生物工程学报, 2021, 37(4): 1120–1130. doi: 10.13345/J.cjb.200408YANG Shan, LI Jinyu, CUI Yujun, et al. The current status and future prospects of DNA computing[J]. Chinese Journal of Biotechnology, 2021, 37(4): 1120–1130. doi: 10.13345/J.cjb.200408 [3] 赵云彬, 周士华. DNA逻辑计算模型的研究现状与展望[J]. 计算机应用研究, 2019, 36(11): 3201–3209. doi: 10.19734/j.issn.1001-3695.2018.07.0512ZHAO Yunbin and ZHOU Shihua. Research status and prospect of DNA-based logic computing models[J]. Application Research of Computers, 2019, 36(11): 3201–3209. doi: 10.19734/j.issn.1001-3695.2018.07.0512 [4] ADLEMAN L M. Molecular computation of solutions to combinatorial problems[J]. Science, 1994, 266(5187): 1021–1024. doi: 10.1126/science.7973651 [5] WANG Yanfeng, WANG Panru, HUANG Chun, et al. Five-input cube-root logical operation based on DNA strand displacement[J]. Journal of Nanoelectronics and Optoelectronics, 2018, 13(6): 831–838. doi: 10.1166/jno.2018.2324 [6] WANG Yanfeng, LI Zhi, and SUN Junwei. Three-variable chaotic oscillatory system based on DNA strand displacement and its coupling combination synchronization[J]. IEEE Transactions on NanoBioscience, 2020, 19(3): 434–445. doi: 10.1109/TNB.2020.2989577 [7] 周万琦, 仇虎, 郭宇锋, 等. 基于二维材料纳米孔的生物传感器: 计算和模拟研究进展[J]. 科学通报, 2021, 66(6): 657–673. doi: 10.1360/TB-2020-1051ZHOU Wanqi, QIU Hu, GUO Yufeng, et al. Two-dimensional material nanopores as biosensors: Recent progress based on computations and simulations[J]. Chinese Science Bulletin, 2021, 66(6): 657–673. doi: 10.1360/TB-2020-1051 [8] 王君珂, 印珏, 牛人杰, 等. DNA计算与DNA纳米技术[J]. 电子与信息学报, 2020, 42(6): 1313–1325. doi: 10.11999/JEIT190826WANG Junke, YIN Yu, NIU Renjie, et al. DNA computing and DNA nanotechnology[J]. Journal of Electronics &Information Technology, 2020, 42(6): 1313–1325. doi: 10.11999/JEIT190826 [9] 张文彬. DNA纳米机器: 梦想照进现实[J]. 高分子学报, 2021, 52(4): 335–338. doi: 10.11777/j.issn1000-3304.2020.20275ZHANG Wenbin. DNA Nano-robot: What dreams may come[J]. Acta Polymerica Sinica, 2021, 52(4): 335–338. doi: 10.11777/j.issn1000-3304.2020.20275 [10] 赵彦, 郭琳洁, 代江兵, 等. DNA纳米结构在药物转运载体和智能载药中的应用进展[J]. 分析化学, 2017, 45(7): 1078–1087. doi: 10.11895/j.issn.0253-3820.170157ZHAO Yan, GUO Linjie, DAI Jiangbing, et al. Application progress of DNA nanostructures in drug delivery and smart drug carriers[J]. Chinese Journal of Analytical Chemistry, 2017, 45(7): 1078–1087. doi: 10.11895/j.issn.0253-3820.170157 [11] TASCIOTTI E. Smart cancer therapy with DNA origami[J]. Nature Biotechnology, 2018, 36(3): 234–235. doi: 10.1038/nbt.4095 [12] 斯燕方, 殷志祥, 崔建中, 等. 简单0-1规划问题的动态DNA折纸计算模型[J]. 计算机工程与应用, 2020, 56(4): 168–174. doi: 10.3778/j.issn.1002-8331.1812-0293SI Yanfang, YIN Zhixiang, CUI Jianzhong, et al. Dynamic DNA origami computing model for simple 0-1 programming problem[J]. Computer Engineering and Applications, 2020, 56(4): 168–174. doi: 10.3778/j.issn.1002-8331.1812-0293 [13] 李伟哲, 刘露, 张辉, 等. PCR技术在水产动物疾病检测中的应用[J]. 水产科学, 2019, 38(5): 726–733. doi: 10.16378/j.cnki.1003-1111.2019.05.021LI Weizhe, LIU Lu, ZHANG Hui, et al. Applications of PCR technology in diseases diagnosis in aquaculture animals[J]. Fisheries Science, 2019, 38(5): 726–733. doi: 10.16378/j.cnki.1003-1111.2019.05.021 [14] SU Haomiao, XU Jinglei, WANG Qi, et al. High-efficiency and integrable DNA arithmetic and logic system based on strand displacement synthesis[J]. Nature Communications, 2019, 10(1): 5390. doi: 10.1038/S41467-019-13310-2 [15] ZOU Chengye, WEI Xiaopeng, ZHANG Qiang, et al. Four-analog computation based on DNA strand displacement[J]. ACS Omega, 2017, 2(8): 4143–4160. doi: 10.1021/acsomega.7b00572 [16] LIU Na, XU Kai, LIU Liquan, et al. A star-shaped DNA probe based on strand displacement for universal and multiplexed fluorometric detection of genetic variations[J]. Microchimica Acta, 2018, 185(9): 413. doi: 10.1007/s00604-018-2941-0 [17] YAN Shankai and WONG K C. Future DNA computing device and accompanied tool stack: Towards high-throughput computation[J]. Future Generation Computer Systems, 2021, 117: 111–124. doi: 10.1016/j.future.2020.10.038 [18] QIAN Lulu and WINFREE E. Scaling up digital circuit computation with DNA strand displacement cascades[J]. Science, 2011, 332(6034): 1196–1201. doi: 10.1126/science.1200520 [19] SONG Tianqi, ESHRA A, SHAH S, et al. Fast and compact DNA logic circuits based on single-stranded gates using strand-displacing polymerase[J]. Nature Nanotechnology, 2019, 14(11): 1075–1081. doi: 10.1038/s41565-019-0544-5 [20] WANG Fei, LV Hui, LI Qian, et al. Implementing digital computing with DNA-based switching circuits[J]. Nature Communications, 2020, 11(1): 121. doi: 10.1038/s41467-019-13980-y [21] CARDELLI L. Strand algebras for DNA computing[J]. Natural Computing, 2011, 10(1): 407–428. doi: 10.1007/s11047-010-9236-7 [22] LAKIN M R, YOUSSEF S, POLO F, et al. Visual DSD: A design and analysis tool for DNA strand displacement systems[J]. Bioinformatics, 2011, 27(22): 3211–3213. doi: 10.1093/bioinformatics/btr543 -





 下载:
下载:



 下载:
下载:
