| [1] |
YOU Xiaohu, WANG Chengxiang, HUANG Jie, et al. Towards 6G wireless communication networks: Vision, enabling technologies, and new paradigm shifts[J]. Science China Information Sciences, 2021, 64(1): 110301. doi: 10.1007/s11432-020-2955-6
|
| [2] |
于宝泉, 蔡跃明, 胡健伟. 认知无线电非正交多址接入随机网络物理层安全性能分析[J]. 电子与信息学报, 2020, 42(4): 950–956. doi: 10.11999/JEIT190049YU Baoquan, CAI Yueming, and HU Jianwei. Performance analysis of physical layer security for cognitive radio non-orthogonal multiple access random network[J]. Journal of Electronics &Information Technology, 2020, 42(4): 950–956. doi: 10.11999/JEIT190049
|
| [3] |
雷维嘉, 林秀珍, 杨小燕, 等. 利用人工噪声提高合法接收者性能的物理层安全方案[J]. 电子与信息学报, 2016, 38(11): 2887–2892. doi: 10.11999/JEIT160054LEI Weijia, LIN Xiuzhen, YANG Xiaoyan, et al. Physical layer security scheme exploiting artificial noise to improve the performance of legitimate user[J]. Journal of Electronics &Information Technology, 2016, 38(11): 2887–2892. doi: 10.11999/JEIT160054
|
| [4] |
HUANG Chongwen, HU Sha, ALEXANDROPOULOS G C, et al. Holographic MIMO surfaces for 6G wireless networks: Opportunities, challenges, and trends[J]. IEEE Wireless Communications, 2020, 27(5): 118–125. doi: 10.1109/MWC.001.1900534
|
| [5] |
WU Qingqing and ZHANG Rui. Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network[J]. IEEE Communications Magazine, 2020, 58(1): 106–112. doi: 10.1109/MCOM.001.1900107
|
| [6] |
CUI Miao, ZHANG Guangchi, and ZHANG Rui. Secure wireless communication via intelligent reflecting surface[J]. IEEE Wireless Communications Letters, 2019, 8(5): 1410–1414. doi: 10.1109/LWC.2019.2919685
|
| [7] |
CHU Zheng, HAO Wanming, XIAO Pei, et al. Intelligent reflecting surface aided multi-antenna secure transmission[J]. IEEE Wireless Communications Letters, 2020, 9(1): 108–112. doi: 10.1109/LWC.2019.2943559
|
| [8] |
CHEN Jie, LIANG Yingchang, PEI Yiyang, et al. Intelligent reflecting surface: A programmable wireless environment for physical layer security[J]. IEEE Access, 2019, 7: 82599–82612. doi: 10.1109/ACCESS.2019.2924034
|
| [9] |
YU Xianghao, XU Dongfang, SUN Ying, et al. Robust and secure wireless communications via intelligent reflecting surfaces[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(11): 2637–2652. doi: 10.1109/JSAC.2020.3007043
|
| [10] |
YANG Liang, YANG Jinxia, XIE Wenwu, et al. Secrecy performance analysis of RIS-aided wireless communication systems[J]. IEEE Transactions on Vehicular Technology, 2020, 69(10): 12296–12300. doi: 10.1109/TVT.2020.3007521
|
| [11] |
ZHANG Haiyang, HUANG Yongming, LI Chunguo, et al. Secure beamforming design for SWIPT in MISO broadcast channel with confidential messages and external eavesdroppers[J]. IEEE Transactions on Wireless Communications, 2016, 15(11): 7807–7819. doi: 10.1109/TWC.2016.2607705
|
| [12] |
CHEN Gaojie, COON J P, and DI RENZO M. Secrecy outage analysis for downlink transmissions in the presence of randomly located eavesdroppers[J]. IEEE Transactions on Information Forensics and Security, 2017, 12(5): 1195–1206. doi: 10.1109/TIFS.2017.2656462
|
| [13] |
GUAN Xinrong, WU Qingqing, and ZHANG Rui. Intelligent reflecting surface assisted secrecy communication: Is artificial noise helpful or not?[J]. IEEE Wireless Communications Letters, 2020, 9(6): 778–782. doi: 10.1109/LWC.2020.2969629
|
| [14] |
GERACI G, SINGH S, ANDREWS J G, et al. Secrecy rates in broadcast channels with confidential messages and external eavesdroppers[J]. IEEE Transactions on Wireless Communications, 2014, 13(5): 2931–2943. doi: 10.1109/TWC.2014.041014.131101
|
| [15] |
XU Xiaoming, HE Biao, YANG Weiwei, et al. Secure transmission design for cognitive radio networks with Poisson distributed eavesdroppers[J]. IEEE Transactions on Information Forensics and Security, 2016, 11(2): 373–387. doi: 10.1109/TIFS.2015.2500178
|
| [16] |
GRADSHTEIN I S and RYZHIK I M. Table of Integrals, Series, and Products[M]. 7th ed. Burlington: Academic Press, 2007: 337–338.
|
| [17] |
HAENGGI M. Stochastic Geometry for Wireless Networks[M]. Cambridge: Cambridge University Press, 2013: 99–102.
|
| [18] |
SADHWANI D, YADAV R N, and AGGARWAL S. Tighter bounds on the Gaussian Q function and its application in Nakagami-m fading channel[J]. IEEE Wireless Communications Letters, 2017, 6(5): 574–577. doi: 10.1109/LWC.2017.2717907
|
| [19] |
ZHOU Gui, PAN Cunhua, REN Hong, et al. A framework of robust transmission design for IRS-Aided MISO communications with imperfect cascaded channels[J]. IEEE Transactions on Signal Processing, 2020, 68: 5092–5106. doi: 10.1109/TSP.2020.3019666
|
| [20] |
ZHANG Shuowen and ZHANG Rui. Capacity characterization for intelligent reflecting surface aided MIMO communication[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(8): 1823–1838. doi: 10.1109/JSAC.2020.3000814
|
| [21] |
CHONG E K P and ŻAK S H. An Introduction to Optimization[M]. 4th ed. New York: John Wiley & Sons, Inc. , 2013: 103–175.
|





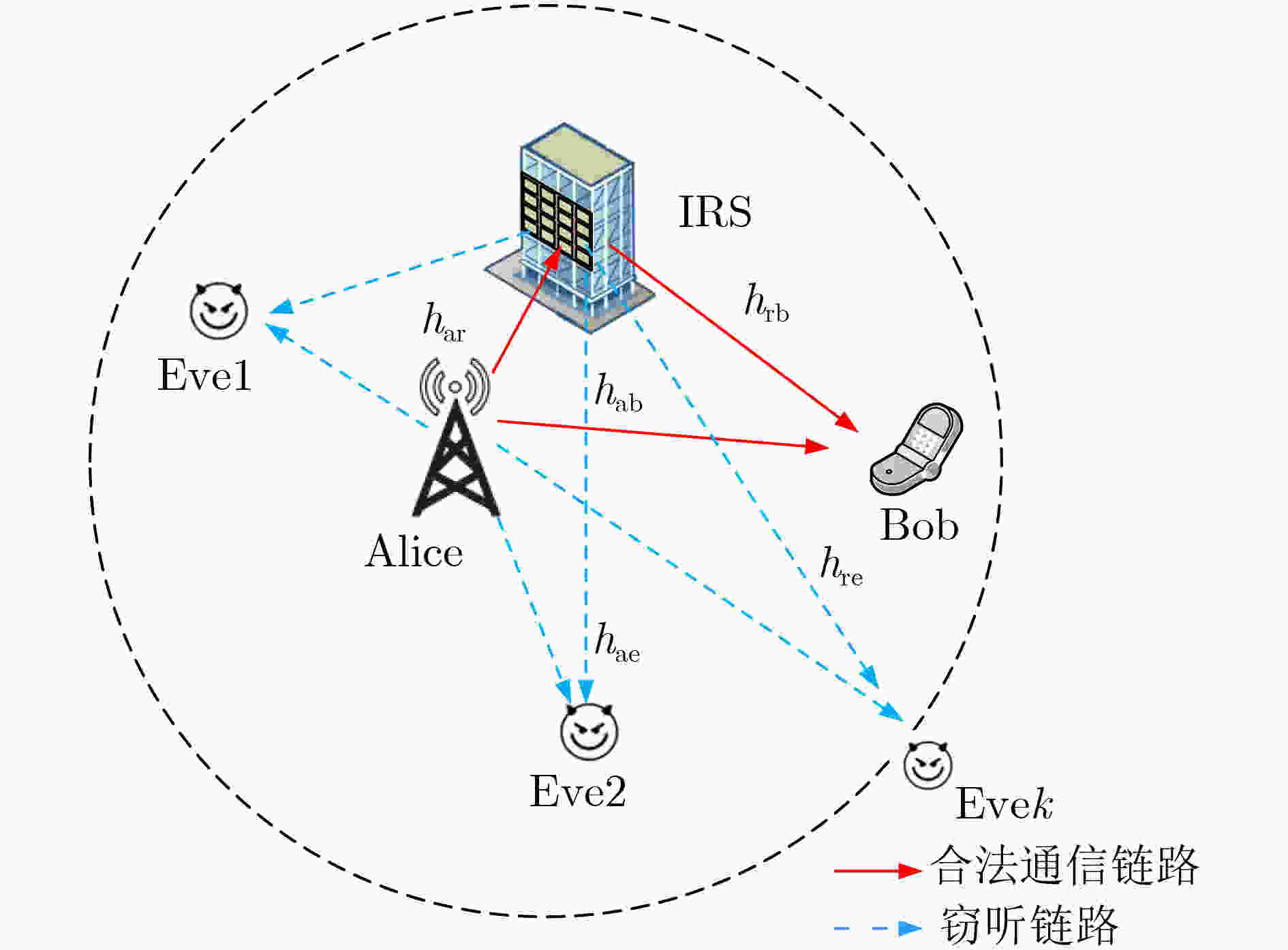
 下载:
下载:
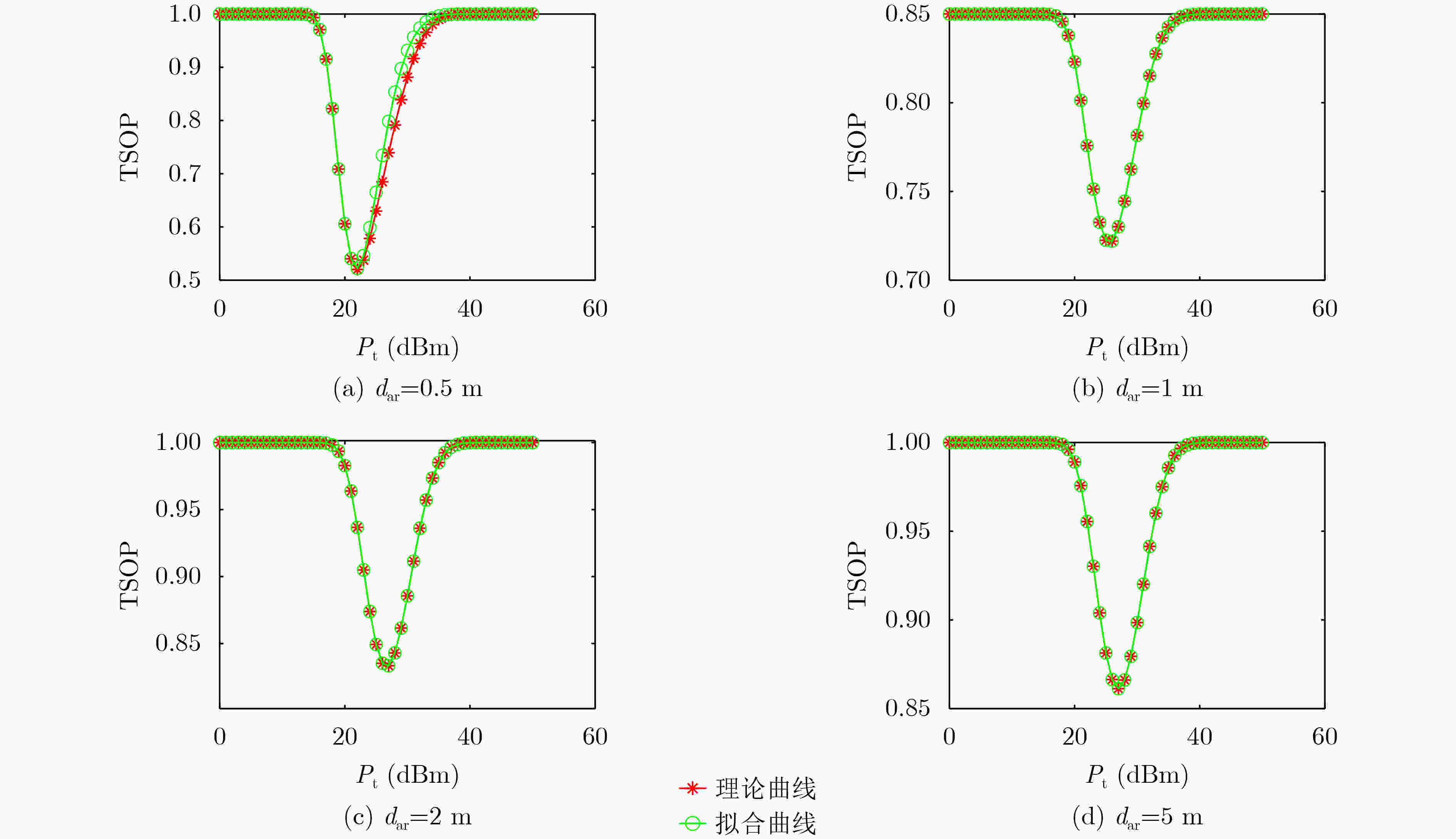

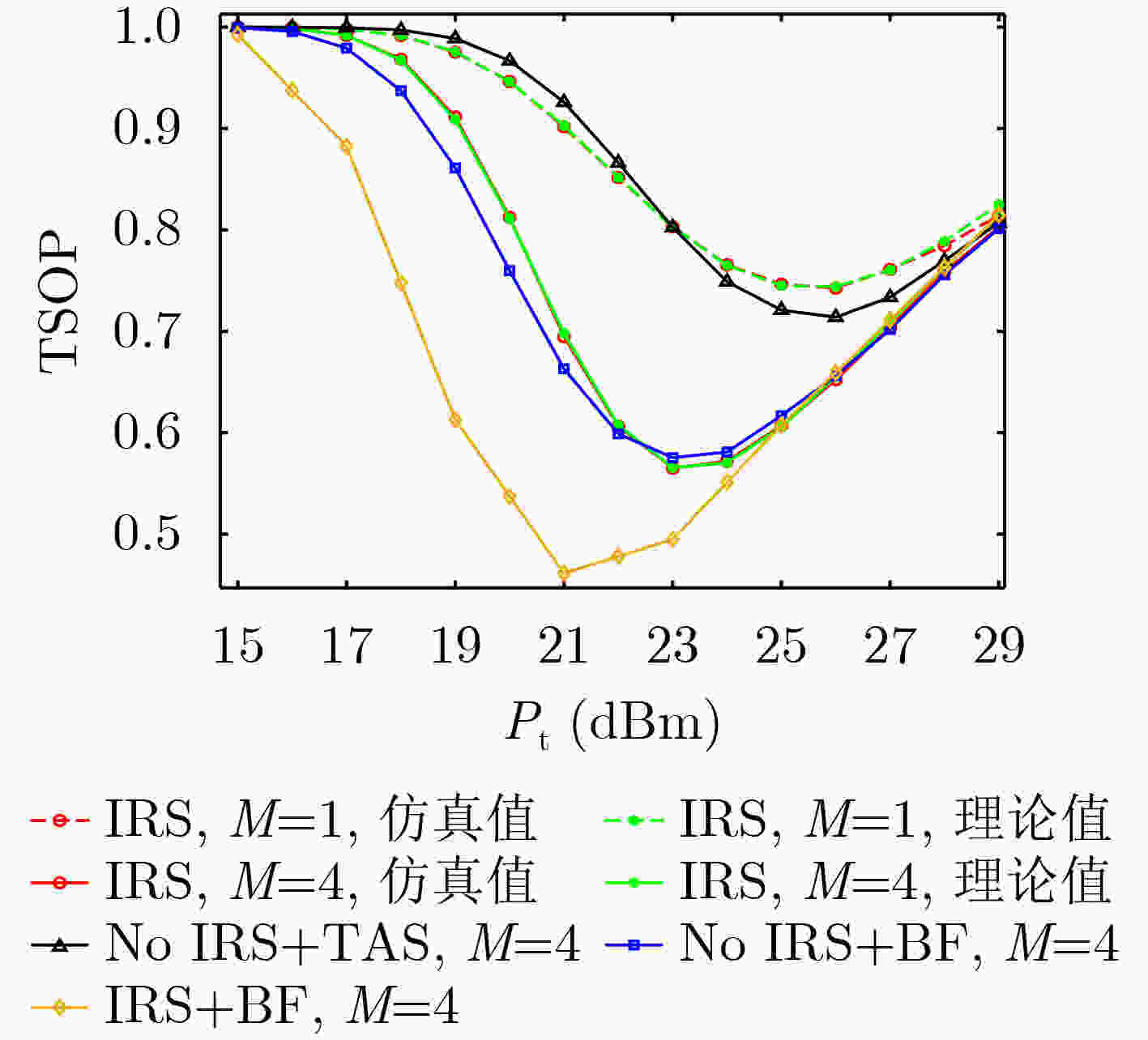
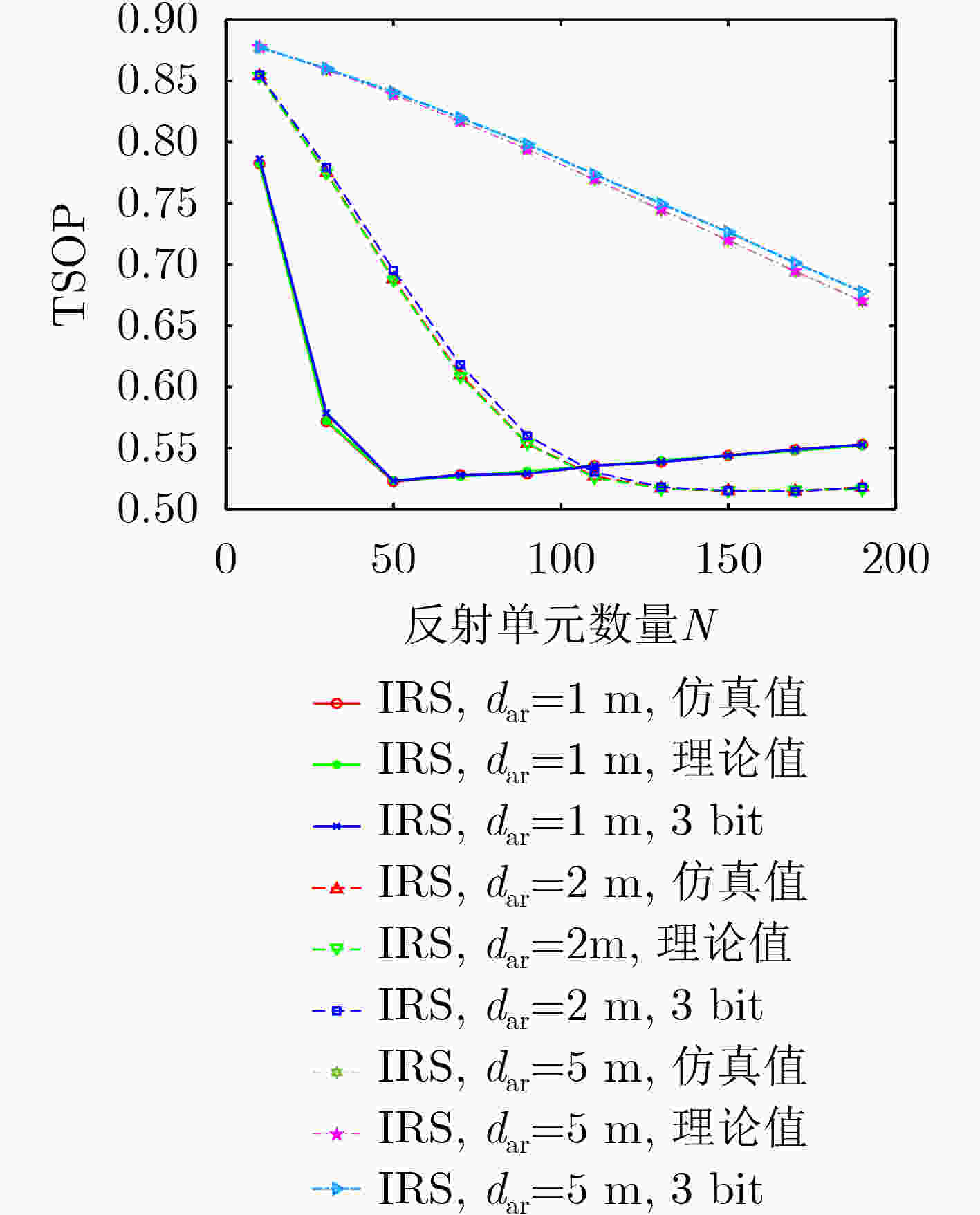


 下载:
下载:
