Research on Material Emergency Scheduling Based on Discrete Whale Swarm Algorithm
-
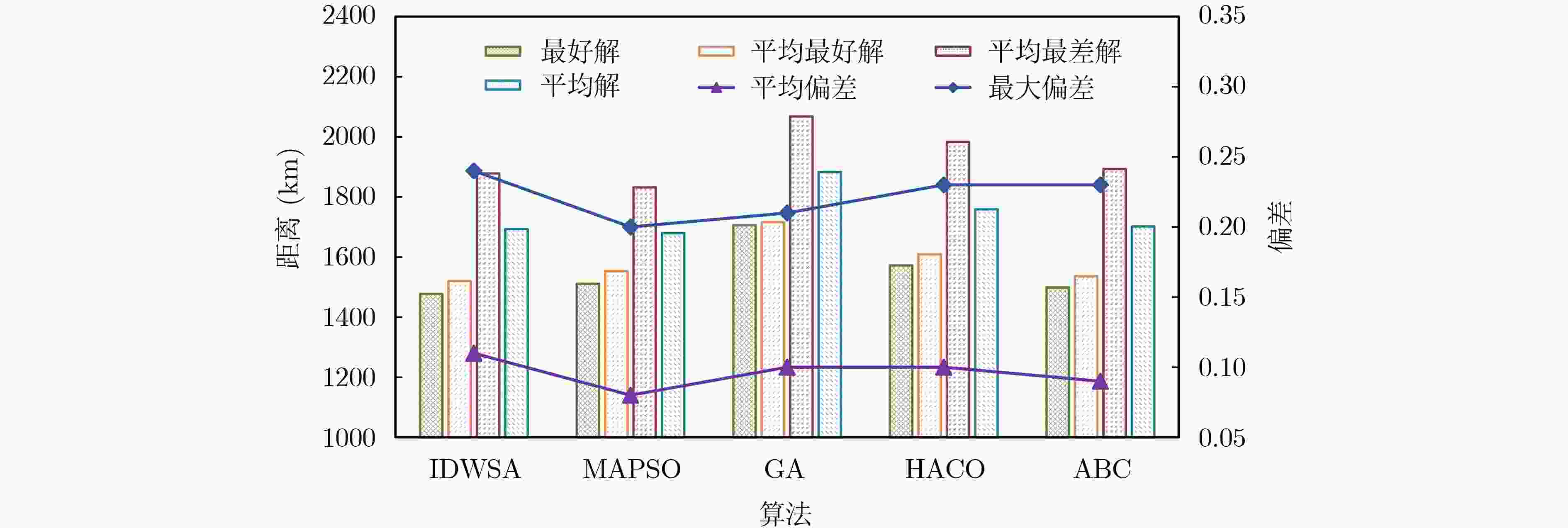
摘要: 针对鲸鱼群算法求解多配送中心带时间窗的物资应急调度问题时存在的易陷入局部极值等缺点,该文提出一种改进离散鲸鱼群算法(IDWSA)。首先采用混合初始化策略提高初始种群的质量;然后构建以相似配送顺序和相同配送中心为比较项的两种移动规则,并设计自适应柯西变异算子和路径选择策略对个体进行移动;最后构造全局评价函数用于选择个体以维持种群多样性。在Solomon标准测试集上,IDWSA所求最好解的距离与MAPSO, GA, HACO, ABC相比分别减少了2.25%, 13.4%, 6%, 1.46%,有效缩短了车辆的行驶距离。Abstract: To overcome the problem of easily falling into local extreme values of the whale swarm algorithm when it solves the material emergency scheduling problem with time windows in multiple distribution centers, an Improved Discrete Whale Swarm Algorithm (IDWSA) is proposed. First, a hybrid initialization strategy is used to improve the quality of the initial population. Then two moving rules with similar distribution order and the same distribution center are constructed as comparison items, and an adaptive Cauchy mutation operator and path selection strategy are designed to move individuals. Finally, a global evaluation function is constructed to select individuals to maintain population diversity. On the Solomon standard test set, the distance of the best solution obtained by IDWSA is reduced by 2.25%,13.4%,6% and 1.46% compared with MAPSO,GA,HACO and ABC, respectively, which shortens effectively the driving distance of the vehicle.
-
表 1 路径选择策略
输入:路径权值矩阵W,未被访问受灾点集合S 输出:可行路径L (1) p=0,L=[0] (2) while len(S)!=0 (3) max=W[p][0], max_index=0 (4) for i=1 to len(S) do (5) if max<W[p][i] then (6) max=W[p][i], max_index=i (7) end if (8) end for (9) L.append(max_index) (10) S.remove(max_index) (11) end while 表 2 数据集配送中心信息
位置 配送中心 1 2 3 x 15 35 53 y 30 60 28 表 3 评价指标及含义
评价指标 含义 最好解/车辆数 不同求解次数中求得的车辆行驶路径的最短总距离/当前解的所用总车辆数 最差解/车辆数 不同求解次数中求得的车辆行驶路径的最长总距离/当前解的所用总车辆数 种群平均解/车辆数 当前种群中所有个体表示的车辆行驶距离的平均值/当前种群所有解的平均总车辆数 平均最好解 所有实验中最好解的平均值 平均最差解 所有实验中最差解的平均值 平均解 所有实验中所求平均解的平均值 平均偏差 (平均解–最好解)/最好解 最大偏差 (最差解–最好解)/最好解 运算时间 每一次实验所耗费的时间 平均运算时间 所有实验次数下算法的平均运行时间 表 4 不同参数下算法所求解的质量
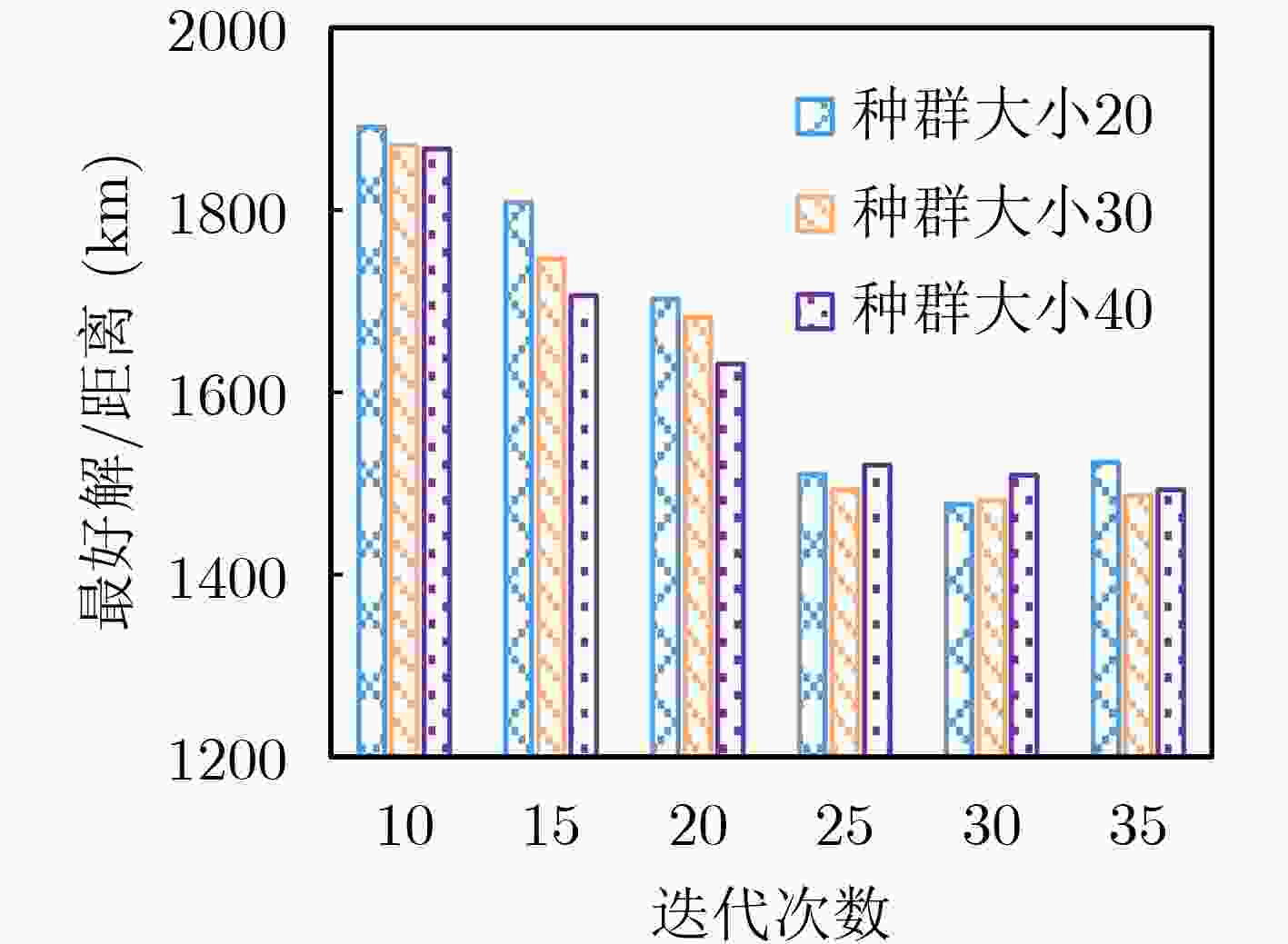
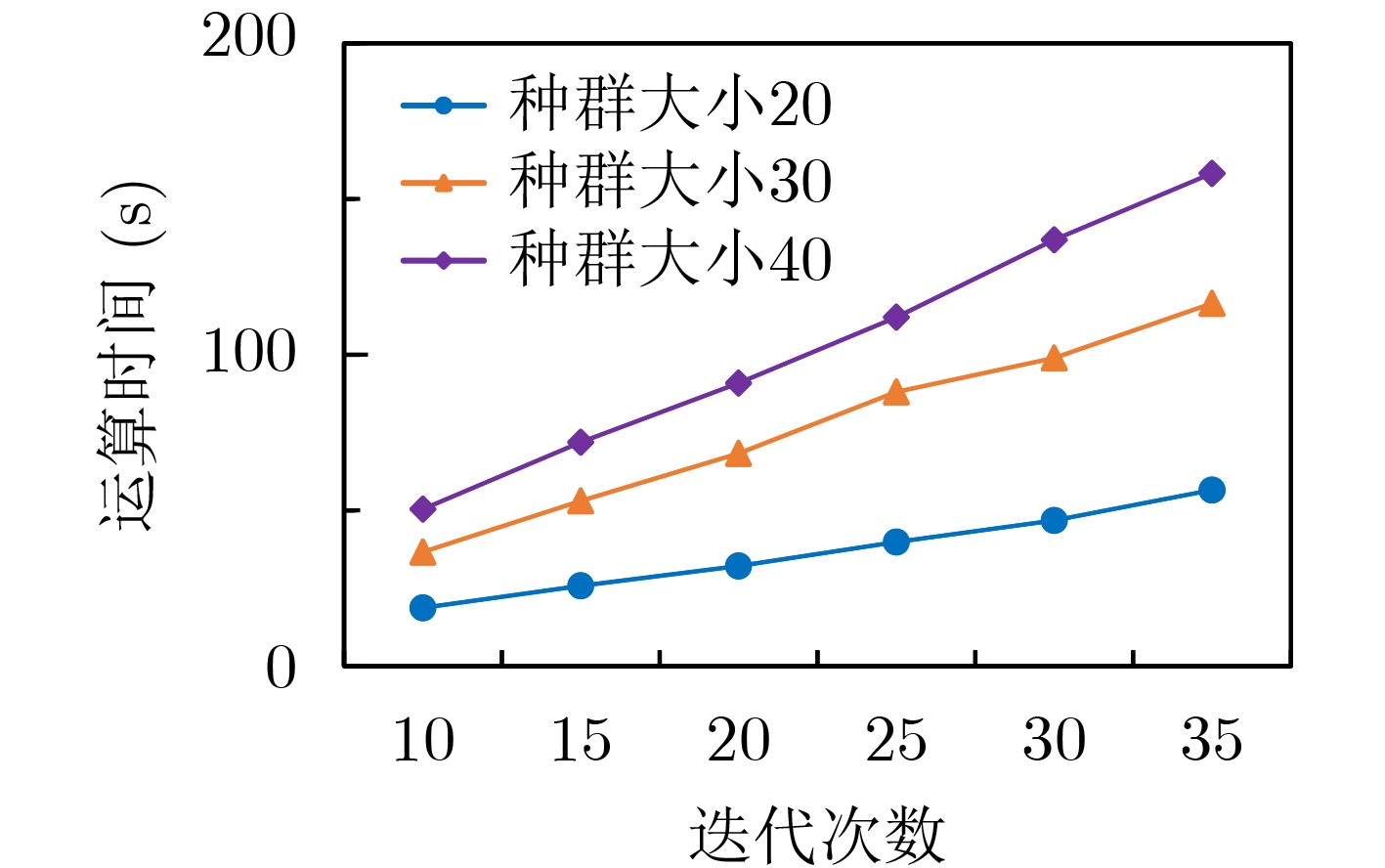
种群大小 迭代次数 平均最好解(km) 平均最差解(km) 平均解(km) 20 10 1966.8 2231.4 2011.35 15 1902.6 2092.2 1944.6 20 1854 2051.2 1907.68 25 1627 2022 1890.43 30 1520 1878 1692.96 35 1579 1927 1743.6 30 10 1881 2051.2 1907.68 15 1752.71 2239.7 1869.97 20 1621.3 1855 1655.52 25 1501.6 2001.95 1713.41 30 1496.2 1956.17 1709.3 35 1499 2016.5 1756.9 40 10 1895 2089 1965.34 15 1723.1 2003.6 1867.6 20 1689 1929 1735.55 25 1534.2 2009.6 1796.5 30 1571.6 2011.2 1801.26 35 1509.32 1967.51 1839.3 表 5 3种种群初始化方式结果对比
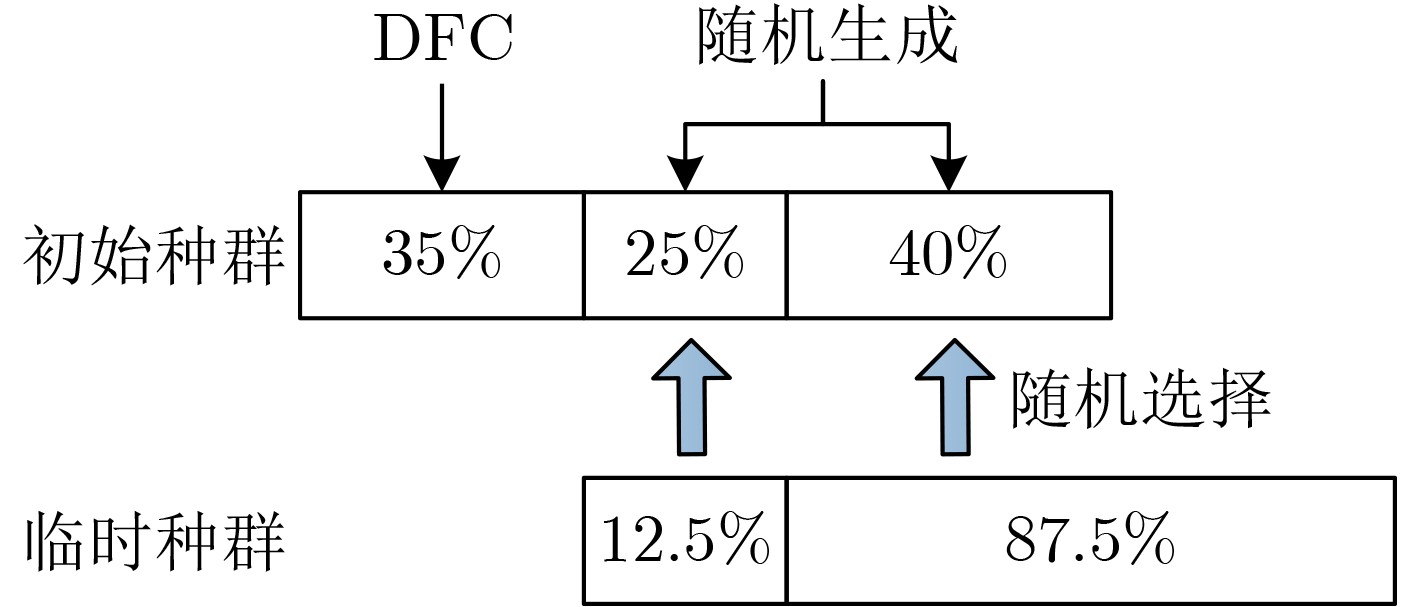
混合初始化策略 DFC 随机生成 初始种群 种群多样性 0.105 0.09 0.12 平均最好解(km) 2172 2333.55 2959.36 平均最差解(km) 3703.13 2685.35 3643.74 平均解(km) 3069.48 2526.38 3407.23 最终解 种群多样性 0.0319 0.02643 0.02943 平均最好解(km) 1520 1794.95 2171.68 平均最差解(km) 1878 1911.77 2461.23 平均解(km) 1692.96 1809.34 2296.54 表 6 两种函数求得可行解
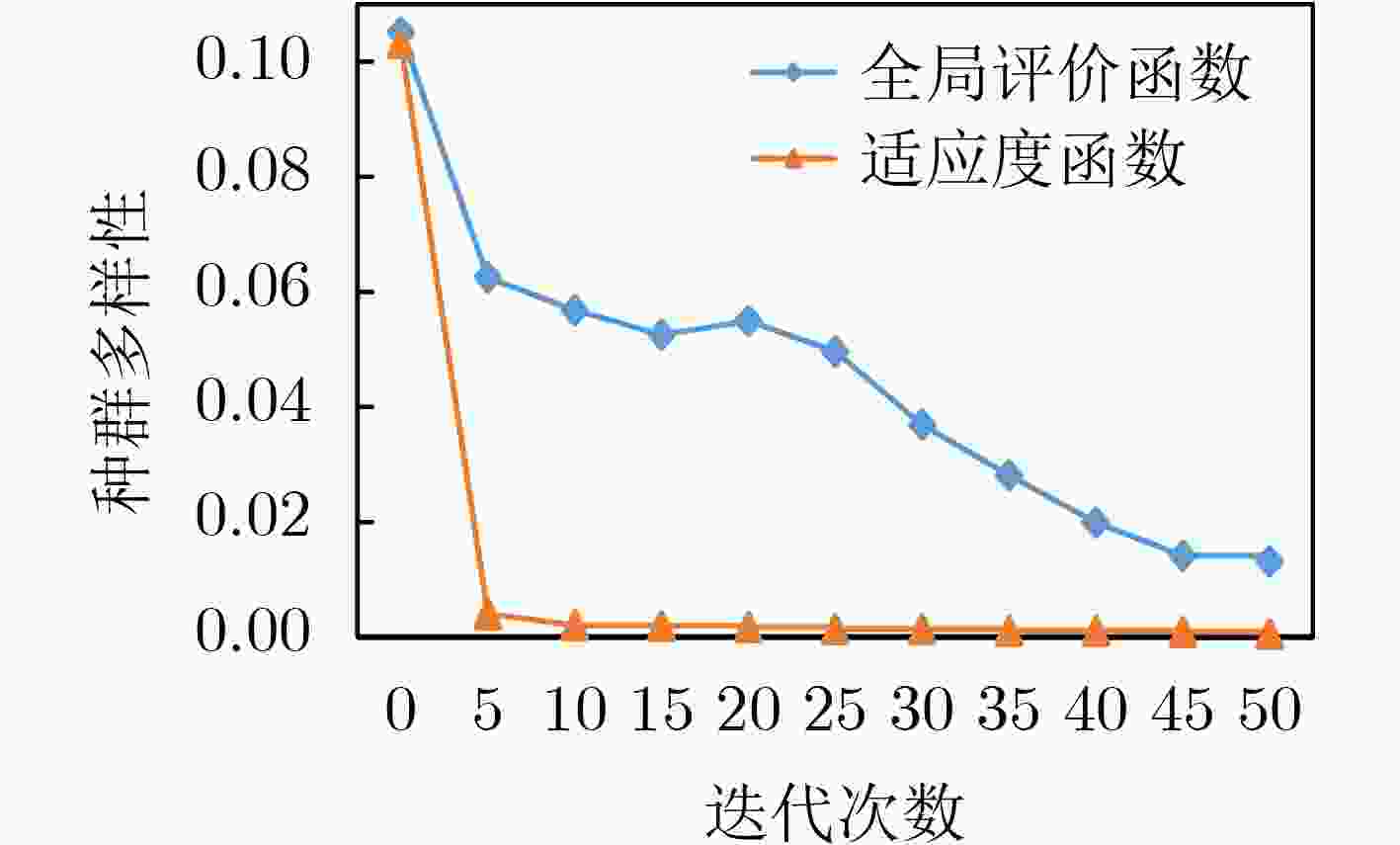
全局评价函数 适应度函数 最好解/车辆数 1477/9 1576/9 最差解/车辆数 1868/10 1927/11 种群平均解/车辆 1672.96/10 1743.6/10 最大偏差 0.26 0.22 平均偏差 0.13 0.10 平均运算时间 46.16 46.31 -
[1] ZHOU Lei, WU Xianhua, XU Zeshui, et al. Emergency decision making for natural disasters: An overview[J]. International Journal of Disaster Risk Reduction, 2018, 27: 567–576. doi: 10.1016/j.ijdrr.2017.09.037 [2] DANTZIG G B and RAMSER J H. The truck dispatching problem[J]. Management Science, 1959, 6(1): 80–91. doi: 10.1287/mnsc.6.1.80 [3] DORLING K, HEINRICHS J, MESSIER G G, et al. Vehicle routing problems for drone delivery[J]. IEEE Transactions on Systems, Man, and Cybernetics:Systems, 2017, 47(1): 70–85. doi: 10.1109/TSMC.2016.2582745 [4] PARADISO R, ROBERTI R, LAGANÁ D, et al. An exact solution framework for multitrip vehicle-routing problems with time windows[J]. Operations Research, 2020, 68(1): 180–198. doi: 10.1287/opre.2019.1874 [5] MUNARI P, MORENO A, DE LA VEGA J, et al. The robust vehicle routing problem with time windows: Compact formulation and branch-price-and-cut method[J]. Transportation Science, 2019, 53(4): 1043–1066. doi: 10.1287/trsc.2018.0886 [6] 刘长石, 申立智, 盛虎宜, 等. 考虑交通拥堵规避的低碳时变车辆路径问题研究[J]. 控制与决策, 2020, 35(10): 2486–2496. doi: 10.13195/j.kzyjc.2019.0257LIU Changshi, SHEN Lizhi, SHENG Huyi, et al. Research on low-carbon time-dependent vehicle routing problem with traffic congestion avoidance approaches[J]. Control and Decision, 2020, 35(10): 2486–2496. doi: 10.13195/j.kzyjc.2019.0257 [7] 张景玲, 刘金龙, 赵燕伟, 等. 时间依赖型同时取送货VRP及超启发式算法[J]. 计算机集成制造系统, 2020, 26(7): 1905–1917. doi: 10.13196/j.cims.2020.07.019ZHANG Jingling, LIU Jinlong, ZHAO Yanwei, et al. Time dependent simultaneous delivery VRP and super heuristic algorithm[J]. Computer Integrated Manufacturing Systems, 2020, 26(7): 1905–1917. doi: 10.13196/j.cims.2020.07.019 [8] MARINAKIS Y, MARINAKI M, and MIGDALAS A. A multi- adaptive particle swarm optimization for the vehicle routing problem with time windows[J]. Information Sciences, 2019, 481: 311–329. doi: 10.1016/j.ins.2018.12.086 [9] RAMACHANDRANPILLAI R and AROCK M. Spiking neural firefly optimization scheme for the capacitated dynamic vehicle routing problem with time windows[J]. Neural Computing and Applications, 2021, 33(1): 409–432. doi: 10.1007/s00521-020-04983-8 [10] LAHYANI R, GOUGUENHEIM A L, and COELHO L C. A hybrid adaptive large neighbourhood search for multi-depot open vehicle routing problems[J]. International Journal of Production Research, 2019, 57(22): 6963–6976. doi: 10.1080/00207543.2019.1572929 [11] 胡蓉, 李洋, 钱斌, 等. 结合聚类分解的增强蚁群算法求解复杂绿色车辆路径问题[J/OL]. 自动化学报. http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c190872, 2020.HU Rong, LI Yang, QIAN bin, et al. Enhanced ant colony algorithm combined with clustering decomposition for solving complex green vehicle routing problem[J/OL]. Acta Automatica Sinica. http://www.aas.net.cn/cn/article/doi/10.16383/j.aas.c190872, 2020. [12] ZHANG Zizhen, QIN Hu, and LI Yanzhi. Multi-objective optimization for the vehicle routing problem with outsourcing and profit balancing[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(5): 1987–2001. doi: 10.1109/TITS.2019.2910274 [13] LONG Jianyu, SUN Zhenzhong, PARDALOS P M, et al. A hybrid multi-objective genetic local search algorithm for the prize-collecting vehicle routing problem[J]. Information Sciences, 2019, 478: 40–61. doi: 10.1016/j.ins.2018.11.006 [14] 骆剑平, 李霞, 陈泯融. 基于改进混合蛙跳算法的CVRP求解[J]. 电子与信息学报, 2011, 33(2): 429–434. doi: 10.3724/SP.J.1146.2010.00328LUO Jianping, LI Xia, and CHEN Minrong. Improved shuffled frog leaping algorithm for solving CVRP[J]. Journal of Electronics &Information Technology, 2011, 33(2): 429–434. doi: 10.3724/SP.J.1146.2010.00328 [15] 李国明, 李军华. 基于混合禁忌搜索算法的随机车辆路径问题[J]. 控制与决策, 2021, 36(9): 2161–2169. doi: 10.13195/j.kzyjc.2020.0107LI Guoming and LI Junhua. Stochastic vehicle routing problem based on hybrid tabu search algorithm[J]. Control and Decision, 2021, 36(9): 2161–2169. doi: 10.13195/j.kzyjc.2020.0107 [16] XIANG Xiaoshu, TIAN Ye, ZHANG Xingyi, et al. A pairwise proximity learning-based ant colony algorithm for dynamic vehicle routing problems[J]. IEEE Transactions on Intelligent Transportation Systems, To be published. doi: 10.1109/TITS.2021.3052834. [17] SOLOMON M M. VRPTW benchmark problems[EB/OL]. http://w.cba.neu.edu/~msolomon/problems.htm, 2003. [18] ZENG Bing, GAO Liang, and LI Xinyu. Whale swarm algorithm for function optimization[C]. Proceedings of the 13th International Conference on Intelligent Computing Theories and Application, Liverpool, United Kingdom, 2017: 624–639. doi: 10.1007/978-3-319-63309-1_55. [19] PEZZELLA F, MORGANTI G, and CIASCHETTI G. A genetic algorithm for the flexible job-shop scheduling problem[J]. Computers & Operations Research, 2008, 35(10): 3202–3212. doi: 10.1016/j.cor.2007.02.014 [20] GAO Kaizhou, SUGANTHAN P N, PAN Quanke, et al. An improved artificial bee colony algorithm for flexible job-shop scheduling problem with fuzzy processing time[J]. Expert Systems with Applications, 2016, 65: 52–67. doi: 10.1016/j.eswa.2016.07.046 [21] 张国辉, 高亮, 李培根, 等. 改进遗传算法求解柔性作业车间调度问题[J]. 机械工程学报, 2009, 45(7): 145–151. doi: 10.3901/JME.2009.07.145ZHANG Guohui, GAO Liang, LI Peigen, et al. Improved genetic algorithm for the flexible job-shop scheduling problem[J]. Journal of Mechanical Engineering, 2009, 45(7): 145–151. doi: 10.3901/JME.2009.07.145 [22] WANG Kangzhou, LAN Shulin, and ZHAO Yingxue. A genetic-algorithm-based approach to the two-echelon capacitated vehicle routing problem with stochastic demands in logistics service[J]. Journal of the Operational Research Society, 2017, 68(11): 1409–1421. doi: 10.1057/s41274-016-0170-7 [23] ZHANG Huizhen, ZHANG Qinwan, MA Liang, et al. A hybrid ant colony optimization algorithm for a multi-objective vehicle routing problem with flexible time windows[J]. Information Sciences, 2019, 490: 166–190. doi: 10.1016/j.ins.2019.03.070 [24] GU Zhaoquan, ZHU Yan, WANG Yuexuan, et al. Applying artificial bee colony algorithm to the multidepot vehicle routing problem[J]. Software: Practice and Experience, 2020. doi: 10.1002/spe.2838. -





 下载:
下载:



 下载:
下载:
