Tunable Diode Laser Absorption Tomography Based on Hierarchical Discretization and Residual Network
-
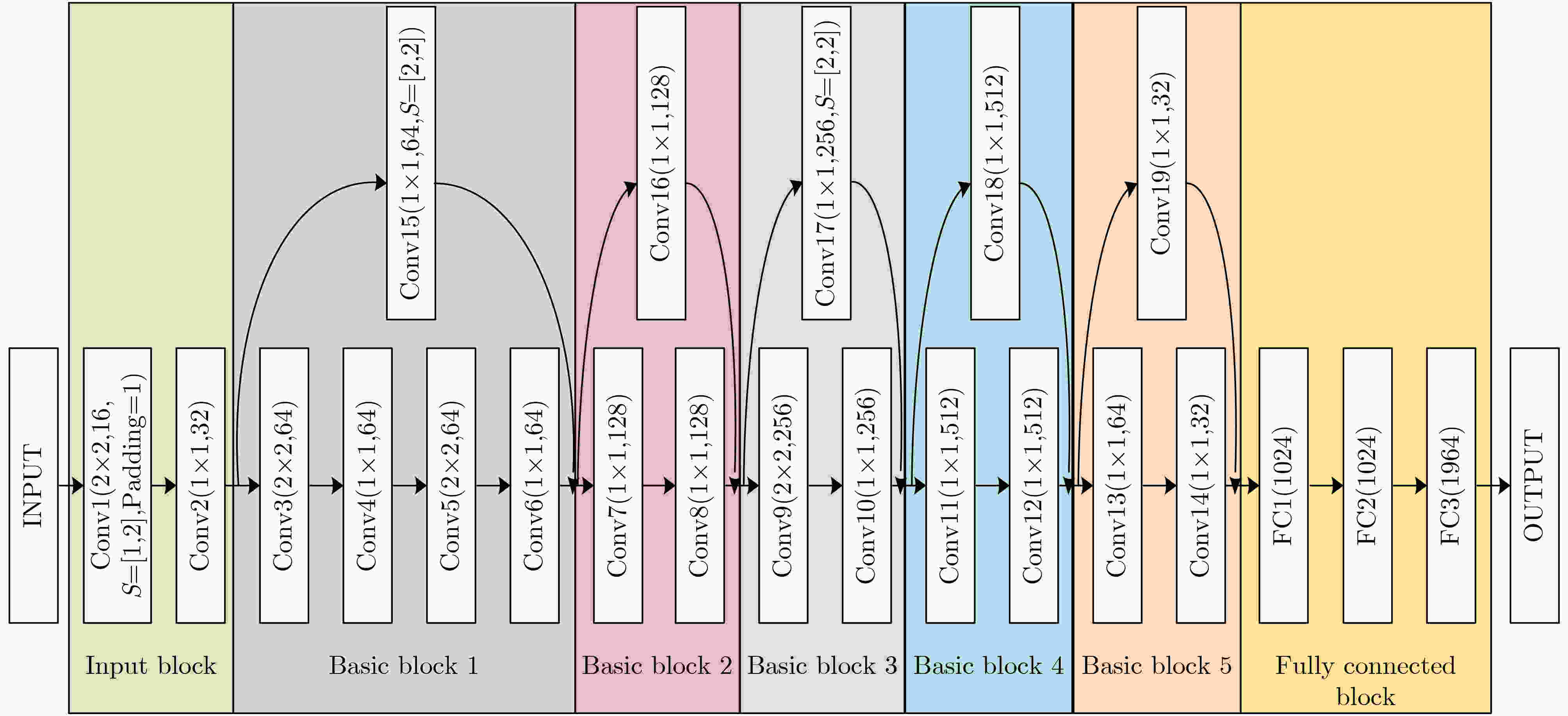
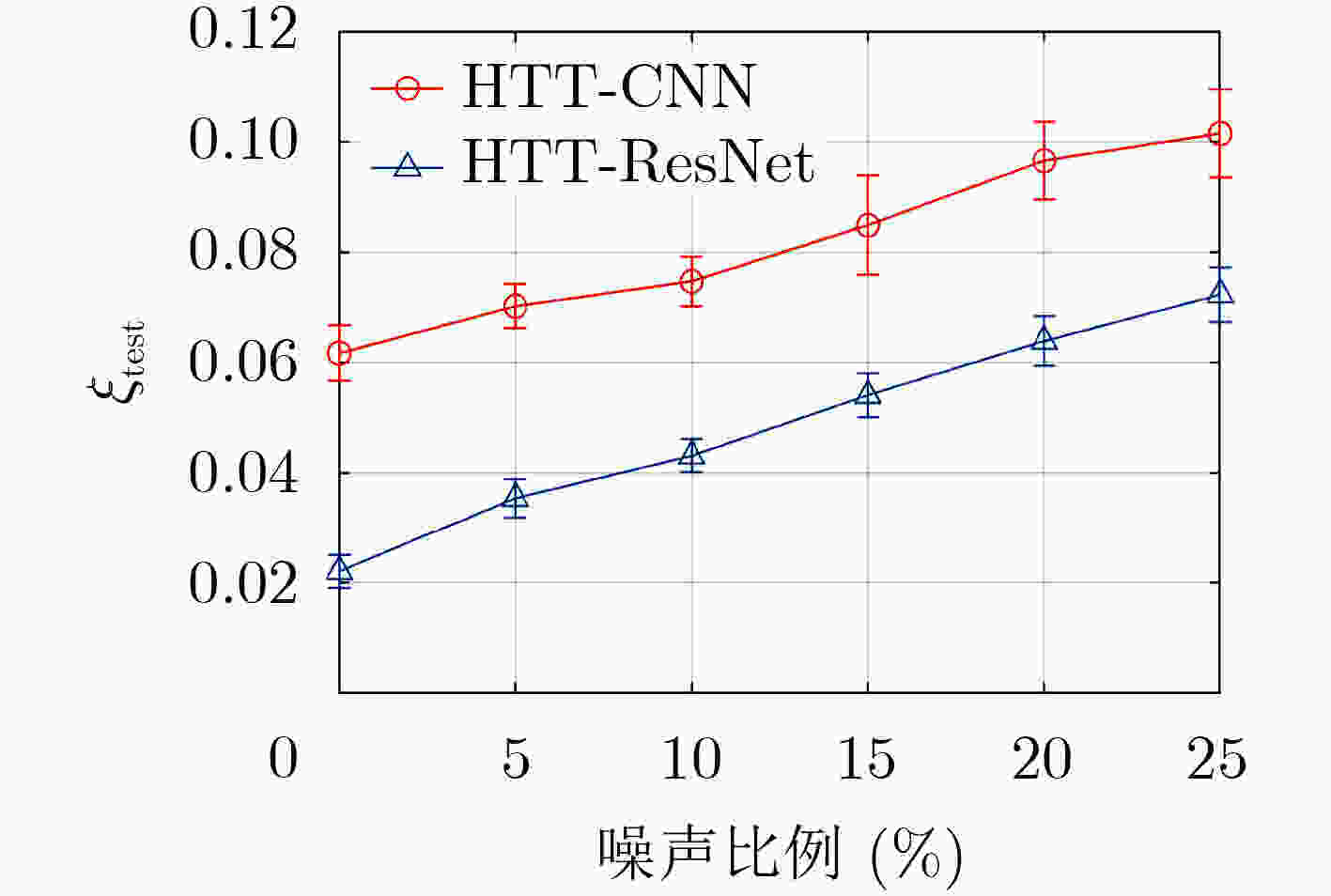
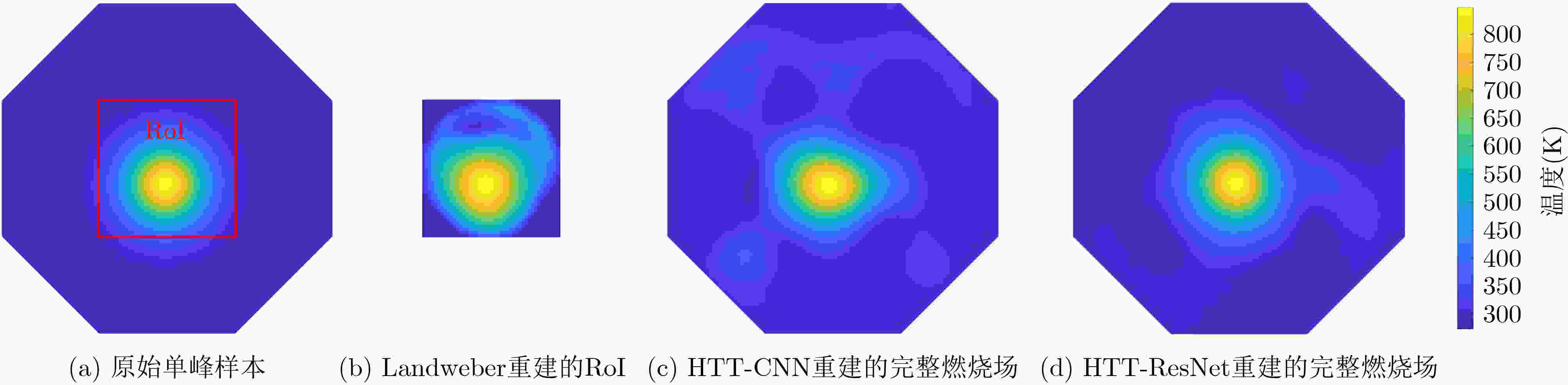
摘要: 快速、准确、适用性强的重建算法是可调谐二极管激光吸收光谱层析成像(TDLAT)的核心研究内容之一。现有算法一般取位于燃烧场中心的某局部区域作为感兴趣区域(RoI)，利用整个燃烧场对激光束的光谱吸收值重建RoI这一局部区域内的气体参数分布。重建结果与实际情况存在一定偏差。针对这一问题，该文研究燃烧场的空间层次化离散方法，进而为TDLAT系统设计一种基于残差网络(ResNet)的层次化温度层析成像方案(HTT-ResNet)。该方案能够根据有限数量的光谱吸收测量值完整重建整个燃烧场的温度图像，并对计算资源与燃烧场不同空间区域的成像分辨率进行优化配置，着重实现RoI内温度分布的高空间分辨率成像。利用随机多模态高斯火焰模型与实际TDLAT系统测量数据进行的实验均表明，HTT-ResNet重建的温度图像能够准确定位火焰的空间位置、清晰描述燃烧场的温度分布。
-
关键词:
- 可调谐二极管激光吸收光谱层析成像 /
- 深度学习 /
- 残差网络 /
- 层次化离散
Abstract: Implementation of fast, accurate and adaptable reconstruction is one of the core topics in Tunable Diode Laser Absorption Tomography (TDLAT). In existing algorithms, a certain region at the center of combustion field is usually set as the Region of Interest (RoI). Temperature image of RoI is reconstructed from the absorbance for laser beams passing through the whole tomographic field. It will cause deviations in the reconstructed image. To address this issue, a spatial hierarchical discretization and a Hierarchical Temperature Tomography scheme based on Residual Network (HTT-ResNet) are proposed for TDLAT. It reconstructs the temperature image of the entire combustion field from limited amount of absorbance measurements, and configures optimally computational resources and imaging resolution to describe the temperature distribution in RoI with better spatial resolution. Experiments using random multimodal Gaussian flame models and the measured data of the actual TDLAT system both show that temperature images reconstructed by HTT-ResNet can accurately locate the flame and clearly describe the temperature profile in the combustion field. -
1. 引言
可调谐二极管激光吸收光谱层析成像(Tunable Diode Laser Absorption Tomography, TDLAT)[1,2]是一种重要的光学非入侵式燃烧诊断技术。利用多光路测量数据重建非均匀的2维温度分布是TDLAT系统中的重要环节。然而，这一反问题具有病态性、数据包含不完全等问题。现有的TDLAT温度重建算法主要分为线性算法和非线性算法两大类。其中，线性算法建立在传统断层扫描理论的基础上，根据沿光路(Line-Of-Sight, LOS)投影出的积分吸收值，重建燃烧场中的气体吸收系数，进而根据对吸收光的分析处理获得温度分布。主流算法主要包括滤波反投影(Filtered Back Projection, FBP)、代数重建算法(Algebraic Reconstruction Technique, ART)、同时迭代重建技术(Simultaneous Iterative Reconstruction Technique, SIRT)和Landweber迭代法等[3]。这类算法通常需要较大数量的LOS投影。然而，实际燃烧设备内有限的空间限制了可布置的激光束的数量，从而限制了这类算法的重建性能。非线性算法直接以燃烧场温度参数为变量建立非线性优化问题，并基于最优化理论重建温度分布，降低了对LOS投影数量的要求。现有算法主要包括模拟退火[4]等。然而，当应用于在线燃烧监测时，这些算法较低的计算效率无法与巨大的数据吞吐量相匹配。
随着人工智能的发展，深度学习的研究与应用正成为模式识别、自动控制、故障诊断[5]等相关领域的热点。在光学成像领域，深度学习逐渐被应用于多种断层扫描反问题的求解中[6-9]。TDLAT系统生成的高吞吐量断层扫描数据虽然为利用传统重建算法实现实时数据处理提出了巨大的挑战，但却为学习和利用历史数据的特征、加快未来的数据处理速度提供了便利。近年来，学者们初步尝试了将深度学习理论与技术引入TDLAT系统的反问题求解领域。Yu等人[10]将深度学习应用于基于TDLAT的燃烧诊断，设计了一种基于极限学习机的线性重建算法。Huang等人[11]提出了一种基于卷积神经网络(Convolutional Neural Network, CNN)的非线性吸收光谱层析重建算法。该算法利用3个频率、6个投影方向、每个方向上40条平行激光束获得的共6 × 40 × 3个LOS投影数据，重建燃烧场中心40 × 40像素的感兴趣区域(Region of Interest, RoI)上的温度分布图像。随后，Huang等人[12]将本征正交分解引入CNN的输出层，进一步降低了CNN网络训练的时间与存储容量消耗。与传统重建算法相比，基于深度学习的TDLAT重建算法能够以较少数量的LOS测量数据实现较高质量的重建，且以优化训练出的网络运算实现的重建算法具有较高的计算效率。
然而，现有的基于深度学习的TDLAT重建方案需要投影角度数大于等于6[11,12]。这一要求在测量空间受限的燃烧诊断环境中很难实现。另一方面，现有算法一般取被测空间的某中心区域为RoI，根据整个被测空间对激光束的吸收值，对RoI这一局部区域内的温度分布进行重建，重建结果存在偏差。相反，若取整个被测区域为RoI，利用现有算法在均匀离散的基础上进行重建，则未知数的显著增加会加剧反问题的病态本质，影响重建质量。此外，与普通CNN相比，残差网络(Residual Network, ResNet)能缓解网络加深所带来的梯度爆炸和梯度消失等问题[13]，具有更强的高维函数拟合能力。针对以上问题，本文基于深度学习，为激光束数量受限的燃烧监测环境，研究符合燃烧场实际气体光谱吸收特性的TDLAT温度成像技术。在为待测燃烧场构建空间层次化离散模型的基础上，提出一种基于残差网络的层次化温度层析成像方案(Hierarchical Temperature Tomography based on ResNet, HTT-ResNet)。本方案对计算资源与燃烧场不同空间区域的成像分辨率进行优化配置，在完整重建被测区域温度分布的基础上，以高空间分辨率重点描述RoI内的温度分布。利用随机多模态高斯火焰模型与实际TDLAT系统测量数据进行的实验均表明，与现有的基于CNN的温度场层析成像方法相比，HTT-ResNet方案重建图像的准确性更高，且对测量噪声具有更强的鲁棒性。
2. 问题模型
根据Beer-Lambert吸收定律，当一束频率为v的激光束穿过长度为L的被测气体时，一部分光强将被吸收，路径积分吸收值(path integrated absorbance)
Av 可以表示为Av=P∫L0C(l)Sv(T(l))dl=∫L0av(l)dl (1) 其中，
av(l) 为Av 在l 处的密度，P为被测区域的压力，T(l) 为l 处的温度，C(l) 为l 处的气体浓度，Sv(⋅) 为跃迁时的吸收谱线的线强度。如图1所示，若将被测区域离散化成J 个等分网格，并假设每个网格内的气体参数是均匀的，则穿过被测区域的频率为v 的第n 条激光束的路径积分吸收值Av,n 可以表示为Av,n=J∑j=1av,jLn,j=PJ∑j=1CjSv(Tj)Ln,j (2) 其中，
av,j 为频率v 下第j 个网格的气体吸收系数，Ln,j 为第n 条激光束穿过第j 个网格的弦长，Tj 和Cj 分别为第j 个网格上的气体温度值与浓度值。若令N 表示激光束数量，则路径积分吸收值向量Av=[Av,1,Av,2,⋯,Av,N]T 与吸收系数向量av=[av,1,av,2,⋯,av,J]T 的关系可以表示为Av=Lav (3) 其中，
L=[Ln,j]∈RN×J 为弦长矩阵。若令温度向量T=[T1,T2,⋯,TJ]T 、浓度向量C=[C1,C2,⋯,CJ]T ，则有av=PC⊙Sv(T) (4) 其中，
⊙ 表示对应元素相乘。Av 与T ,C 间的关系可以进一步表示为Av=PL[C⊙Sv(T)] (5) 为了降低对激光束数量的需求，本文基于深度神经网络研究温度场的非线性重建，即由多条吸收谱线下的路径积分吸收值向量
{Av} 重建温度分布向量T 。另一方面，本文研究燃烧场空间的层次化离散，在完整重建整个待测区域内的温度分布的基础上，以高空间分辨率成像RoI内的温度分布。3. 燃烧场空间的层次化离散模型
本文实际采用的TDLAT系统[14]的测量空间如图2所示。激光光路布置的示意图如图3所示。令
θ 表示激光束与y轴的夹角，本系统在[0∘,180∘) 范围内设置0°, 45°, 90°, 135° 4个角度，在每个角度下布置8条等间距平行激光束，相邻激光束的距离为18 mm，使得测量空间形成边长为144 mm的八边形。选择H2O为被测气体，选取v1=7185.6 cm–1和v2=7444.37 cm–1的两条吸收谱线进行实验研究。若令Nθ ,Nd 和Nv 分别表示角度数、每个角度下的激光束数和谱线数，则Nθ=4 ,Nd=8 ,Nv=2 。本文以如图4所示的方式，对待测燃烧场进行层次化空间离散：取位于燃烧场中心的144 mm× 144 mm区域为RoI，以高密度网格对其进行离散化；对RoI外的区域，以低密度网格进行离散化。具体地，以3.6 × 3.6为单位，将RoI划分为40 × 40个网格；以14.4 × 14.4为单位，将RoI外区域划分为364个网络。设每个网格内的气体特征参数是均匀的。RoI内第
i 个网格内的温度与气体浓度分别用TRoIi 和CRoIi 表示，i=1,2,⋯,NRoI 。RoI外第j 个网格内的温度与气体浓度分别用ToRoIj 和CoRoIj 表示，j=1,2,⋯,NoRoI 。在此层次化空间离散模型的基础上，将频率v 下、第n 条激光束获得的路径积分吸收值Av,n 表示为Av,n=NRoI∑i=1aRoIv,iLRoIn,i+NoRoI∑j=1aoRoIv,jLoRoIn,j=PNRoI∑i=1CRoIiSv(TRoIi)LRoIn,i+PNoRoI∑j=1CoRoIjSv(ToRoIj)LoRoIn,j (6) 其中，以
n=(k−1)Nd+d 作为激光束的序号，对应于第k角度内的第d 条激光束，k=1,2,⋯,Nθ ,d=1,2,⋯,Nd ,n=1,2,⋯,N ,N=NθNd 。aRoIv,i 和aoRoIv,j 分别为频率v 下RoI内第i 个网格和RoI外第j 个网格的气体吸收系数，LRoIn,i 和LoRoIn,j 分别表示第n 条激光束在RoI内第i 个网格和RoI外第j 个网格上的弦长。若令RoI内、RoI外的温度分布向量与浓度分布向量分别为
TRoI=[TRoI1,TRoI2,⋯,TRoINRoI]T ,ToRoI=[ToRoI1,ToRoI2,⋯,ToRoINoRoI]T ,CRoI=[CRoI1,CRoI2,⋯,CRoINRoI]T ,CoRoI=[CoRoI1,CoRoI2,⋯,CoRoINoRoI]T ，则Av 与TRoI ,ToRoI 的关系可以表示为Av=LRoIaRoIv+LoRoIaoRoIv=PLRoI[CRoI⊙Sv(TRoI)]+PLoRoI[CoRoI⊙Sv(ToRoI)] (7) 其中，
aRoIv=[aRoIv,1,aRoIv,2,⋯,aRoIv,NRoI]T 和aoRoIv=[aoRoIv,1,aoRoIv,2,⋯,aoRoIv,NoRoI]T 分别为频率v 下RoI内和RoI外的吸收系数向量；LRoI=[LRoIn,i]∈RN×NRoI 和LoRoI=[LoRoIn,j]∈RN×NoRoI 分别为n条激光束在RoI内和RoI外的弦长矩阵。本文在此层次化离散模型下，构建并优化训练ResNet，据TDLAT系统在
v1 和v2 频率下测量到的有限数量的路径积分吸收值，重建燃烧场层次化温度分布T=[(TRoI)T,(ToRoI)T]T ，进而生成描述燃烧场温度分布的2维图像。此层次化离散模型与温度成像方案适用于一般的TDLAT系统。在对测量场进行层次化离散时，需要令NRoI 明显大于NoRoI ，从而使重建的温度图像中RoI内的空间分辨率明显高于RoI外。为了便于描述，本文以如图2所示的实际TDLAT系统为例。这里，NRoI=1600 ,NoRoI=364 。4. 基于ResNet的燃烧场层次化温度层析成像
本文设计的基于ResNet的层次化温度层析成像方案HTT-ResNet的示意图如图5所示。在ResNet的输入端，将路径积分吸收值向量
Av1 和Av2 分别排列成Nd×Nθ 的矩阵，构成Nd×Nθ×2 的输入。在ResNet的输出端，根据重建出的NRoI+NoRoI 维层次化温度分布向量ˆT 生成温度分布图像。本文构建的ResNet的具体结构如图6所示。该网络由7个模块构成，分别为1个输入块(Input block)、5个基本块(Basic block)和1个全连接块(Fully connected block)，共包含19个卷积层(Conv)和3个全连接层(FC)。第i卷积层Convi(
h×w ,c ,S=[u,v] , Padding)中的参数h×w 表示卷积核的尺寸，c 表示通道数，S=[u,v] 表示卷积核的水平方向滑动步长u 和垂直方向滑动步长v ，Padding为边缘填充的元素数。除特殊说明外，设置各卷积层的S=[1,1] , Padding=0。第j全连接层FCj(n )中的参数n 表示神经元个数。若令
fiConv(⋅) 和fjFC(⋅) 分别表示第i卷积层和第j全连接层的映射函数，则Oi=fiConv(Ii)=σ(Wi∗Ii+bi),i=1,2,⋯,19 (8) Oj=fjFC(Ij)=σ(WjIj+bj),j=1,2,3 (9) 其中，
σ(⋅) 为激活函数，∗ 表示卷积运算，Ii ,Oi ,Wi 和bi 分别表示第i卷积层的输入、输出、卷积核和偏置，Ij ,Oj ,Wj 和bj 分别表示第j全连接层的输入、输出、权重矩阵和偏置。若令
IResNet 表示输入，OInput ,OkBasic 和OResNet 分别表示输入块、第k个基本块和全连接块的输出，则ResNet中各模块的前向传播过程分别为OInput=f2Conv(f1Conv(IResNet)) (10) O1Basic=f6Conv(f5Conv(f4Conv(f3Conv(OInput)))+f15Conv(OInput) (11) O2Basic=f8Conv(f7Conv(O1Basic))+f16Conv(O1Basic) (12) O3Basic=f10Conv(f9Conv(O2Basic))+f17Conv(O2Basic) (13) O4Basic=f12Conv(f11Conv(O3Basic))+f18Conv(O3Basic) (14) O5Basic=f14Conv(f13Conv(O4Basic))+f19Conv(O4Basic) (15) OResNet=f3FC(f2FC(f1FC(O5Basic))) (16) HTT-ResNet根据ResNet输出的层次化温度分布向量
ˆT=[(ˆTRoI)T,(ˆToRoI)T]T=OResNet 生成温度分布图像：以ˆTRoIi 作为重建图像RoI内第i 个像素的像素值，i=1,2,⋯,1600 ；根据ˆToRoIj 进行双3次插值，重建图像RoI外第j 个像素块中的4×4 个像素值，j=1,2,⋯,364 。5. 实验结果与分析
5.1 数据集的建立
构建随机混合高斯火焰模型，生成峰值个数不同、峰值具有随机性、温度与气体浓度分布具有相关性的高斯火焰，从而模拟实际燃烧场中的多模态温度与气体浓度分布，建立数据集。将具有相关性的多特征2维高斯温度分布
T(x,y) 与浓度分布C(x,y) 分别表示成T(x,y)=NG∑l=1λl⋅ul⋅fl(x,y)+Tmin (17) C(x,y) = \sum\limits_{l = 1}^{{N_{\rm{G}}}} {{\lambda _l} \cdot {v_l} \cdot {f_l}\left( {x,y} \right)} + {C_{\min }} (18) 其中，
(x,y) 表示坐标，{N_{\rm{G}}} 为峰值数；{\lambda _l} 是在区间[0.7,1] 上满足均匀分布的随机数，用以调整第l 个高斯分布的权重，l = 1,2,\cdots,{N_{\rm{G}}} 。{u_l} 是在区间\left[ \left\lceil \left( {T_{{\rm{peakL}}}} - {T_{{\rm{min}}}} \right) / {\max \left( {{f_l}(x,y)} \right)} \right\rceil ,\left\lfloor {{{\left( {{T_{{\rm{peakH}}}} - {T_{{\rm{min}}}}} \right)} / {\max \left( {{f_l}(x,y)} \right)}}} \right\rfloor \right] 上满足均匀分布的随机数，{v_l} 是在区间\left[ \left\lceil \left( {C_{{\rm{peakL}}}} - {C_{{\rm{min}}}} \right) / {\max \left( {{f_l}(x,y)} \right)} \right\rceil ,\left\lfloor {{{\left( {{C_{{\rm{peakH}}}} - {C_{{\rm{min}}}}} \right)} / {\max \left( {{f_l}(x,y)} \right)}}} \right\rfloor \right] 上满足均匀分布的随机数，用以分别在\left[ {T_{{\rm{peakL}}}}, {T_{{\rm{peakH}}}} \right] 与\left[ {{C_{{\rm{peakL}}}},{C_{{\rm{peakH}}}}} \right] 的设定范围内随机调整{u_l} \cdot {f_l}\left( {x,y} \right) 与{v_l} \cdot {f_l}\left( {x,y} \right) 的峰值。参数{T_{{\rm{min}}}} 和{C_{{\rm{min}}}} 是为模型设置的温度最小值和浓度最小值。第l 个高斯分布可表示为\begin{split} & {f_l}\left( {x,y} \right) = \frac{1}{{2\pi {\sigma _{l,1}}{\sigma _{l,2}}}}\exp \left[ { - \frac{{{{(x - {\mu _{l,1}})}^2}}}{{2\sigma _{l,1}^2}} - \frac{{{{(y - {\mu _{l,2}})}^2}}}{{2\sigma _{l,2}^2}}} \right] , \\ & \qquad l = 1,2,\cdots,{N_{\rm{G}}}\\[-10pt] \end{split} (19) 其中，均值
{\mu _{l,1}} 和{\mu _{l,2}} 控制高斯峰值在水平和垂直方向上的位置；标准差{\sigma _{l,1}} 和{\sigma _{l,2}} 控制高斯曲面在水平和垂直方向上的跨度。本文在实验中，随机生成4500个单峰火焰样本(
{N_{\rm{G}}}{\rm{ = }}1 )和6400个双峰火焰样本({N_{\rm{G}}}{\rm{ = }}2 )，从而构成数据集{\rm{\{ }}{(({{\boldsymbol{A}}_{v1}},{{\boldsymbol{A}}_{v2}}),{\boldsymbol{T}})_k}:k = 1,2,\cdots,10900\} 。令P为1.013×105 Pa，并将式(17)—式(19)中的参数设置为{T_{{\rm{min}}}}{\rm{ = 300}} ,{C_{{\rm{min}}}}{\rm{ = 0}}{\rm{.01}} ,{T_{{\rm{peakL}}}}{\rm{ = 800}} ,{T_{{\rm{peakH}}}}{\rm{ = 900}} ,{C_{{\rm{peakL}}}}{\rm{ = 0}}{\rm{.11}} ,{C_{{\rm{peakH}}}}{\rm{ = 0}}{\rm{.12}} 。根据如图2所示的实际TDLAT系统的设置，令{\mu _{l,1}} \sim U(34,65) ,{\mu _{l,2}} \sim U(34,65) ,{\sigma _{l,1}} \sim U(10,25) ,{\sigma _{l,2}} \sim U(10,25) ，在保持高斯峰值主体区域位于TDLAT系统测量区域内的同时，尽可能保证样本的多样性。每个样本(({{\boldsymbol{A}}_{v1}},{{\boldsymbol{A}}_{v2}}),{\boldsymbol{T}}) 的具体构建过程如下：(1) 分别按照式(17)、式(18)生成温度矩阵
{{\boldsymbol{T}}_{{\rm{matrix}}}} \in {{\mathbb{R}}^{96 \times 96}} 和浓度矩阵{{\boldsymbol{C}}_{{\rm{matrix}}}} \in {{\mathbb{R}}^{96 \times 96}} ；(2) 根据如图2所示的实际TDLAT系统的设置，利用式(5)计算
{{\boldsymbol{A}}_{v1}} \in {{\mathbb{R}}^{32 \times 1}} 和{{\boldsymbol{A}}_{v2}} \in {{\mathbb{R}}^{32 \times 1}} ；(3) 取
{{\boldsymbol{T}}_{{\rm{matrix}}}} 中心位置处的{\rm{40}} \times {\rm{40}} 矩阵为RoI，将其中数据逐列衔接，构成向量{{\boldsymbol{T}}^{{\rm{RoI}}}} \in {{\mathbb{R}}^{1600 \times 1}} ；(4) 对
{{\boldsymbol{T}}_{{\rm{matrix}}}} 进行1/4 × 1/4的下采样，生成24 × 24的数据矩阵，去除对应于RoI的中心10× 10个元素和每个角上对应于待测区域外的28个元素，对剩余数据按照顺时针顺序逐列扫描，构成向量{{\boldsymbol{T}}^{{\rm{oRoI}}}} \in {{\mathbb{R}}^{364 \times 1}} ；(5) 将
{{\boldsymbol{T}}^{{\rm{RoI}}}} 与{{\boldsymbol{T}}^{{\rm{oRoI}}}} 组成层次化温度分布向量{\boldsymbol{T}}{\rm{ = }}{[{({{\boldsymbol{T}}^{{\rm{RoI}}}})^{\rm{T}}},{({{\boldsymbol{T}}^{{\rm{oRoI}}}})^{\rm{T}}}]^{\rm{T}}} \in {{\mathbb{R}}^{1964 \times 1}} ；(6) 由路径积分吸收值向量
{{\boldsymbol{A}}_{v1}} ,{{\boldsymbol{A}}_{v2}} 和层次化温度分布向量{\boldsymbol{T}} 构成样本(({{\boldsymbol{A}}_{v1}},{{\boldsymbol{A}}_{v2}}),{\boldsymbol{T}}) 。5.2 网络训练与测试
将5.1节构建的数据集
{\rm{\{ }}{(({{\boldsymbol{A}}_{v1}},{{\boldsymbol{A}}_{v2}}),{\boldsymbol{T}})_k}:k = 1, 2,\cdots, 10900\} 中的样本按照8:1:1的比例划分成训练集、验证集与测试集。为了模拟实际测量中测量数据包含的噪声，在路径积分吸收值向量{{\boldsymbol{A}}_{v1}} ,{{\boldsymbol{A}}_{v2}} 上添加0～25%的高斯随机噪声。在不同噪声水平下，分别进行网络训练与测试。定义测试集平均归一化重建误差{\xi _{{\rm{test}}}} 为测试集中所有样本归一化重建误差的平均值，即{\xi _{{\rm{test}}}} = \frac{1}{{{N_{{\rm{test}}}}}}\sum\limits_{k = 1}^{{N_{{\rm{test}}}}} {\frac{{{{\left\| {{{{\hat{\boldsymbol{T}}}}_k} - {{\boldsymbol{T}}_k}} \right\|}_2}}}{{{{\left\| {{{\boldsymbol{T}}_k}} \right\|}_2}}}} (20) 其中，
{N_{{\rm{test}}}} 为测试集中的样本数量，{{\boldsymbol{T}}_k} 和{{\hat{\boldsymbol{T}}}_k} 分别表示第k个样本的真实层次化温度分布向量与重建结果。采用上述数据集，分别对以下两方案进行网络训练与测试，比较方案的重建性能。实验基于MATLAB深度学习框架实现，硬件配置为Intel i7-8750Hz CPU, NVIDA GeForce GTX 1050 Ti GPU, 8 GB内存。
方案1 本文设计的基于层次化离散与ResNet的层次化温度分布重建方案(HTT-ResNet)。网络结构如第4节所述，选用ReLU激活函数。在每轮(epoch)训练前，将训练集随机划分成批次(batch)，使用mini-batch参数更新策略，并进行批归一化(batch normalization)。选用如式(21)所示的L2损失函数
{L_2} = \frac{1}{B}\sum\limits_{b = 1}^B {{{\left\| {{{{\hat{\boldsymbol{T}}}}_b} - {{\boldsymbol{T}}_b}} \right\|}_2}} (21) 其中，B为批大小(batch-size)，
{{\boldsymbol{T}}_b} 和{{\hat{\boldsymbol{T}}}_b} 分别为当前批次第b个训练样本的层次化温度分布向量及其重建结果。实验中，进行100轮训练，批大小设置为128；采用Adam优化器更新参数，学习率设置为0.001；采用L2正则化防止出现过拟合现象，并将惩罚因子设置为{\rm{1}}{{\rm{0}}^{{\rm{ - 4}}}} 。利用优化训练出的网络实现层次化温度重建，以{{\boldsymbol{A}}_{v1}} 和{{\boldsymbol{A}}_{v2}} 为输入，输出层次化温度分布向量{\hat{\boldsymbol{T}}} ，进而重建整个燃烧场的温度分布图像。方案2 利用Huang等人[11]提出的基于CNN的温度重建方案实现层次化温度分布重建(下文中简称为HTT-CNN)。在本文讨论的激光光路布置与燃烧场空间层次化离散模型的基础上，调整Huang等人为RoI内温度分布重建设计的CNN，实现本文讨论的层次化温度分布重建，即以
{{\boldsymbol{A}}_{v1}} 和{{\boldsymbol{A}}_{v2}} 为输入，输出层次化温度分布向量{\hat{\boldsymbol{T}}} ，进而重建整个燃烧场的温度分布图像。超参数设置与网络训练方法采用文献[11]中的最优配置。图7比较了HTT-ResNet与HTT-CNN在0～25%的噪声比例下分别获得的测试集平均归一化重建误差
{\xi _{{\rm{test}}}} 。由图7可见，在各噪声比例下，HTT-ResNet的{\xi _{{\rm{test}}}} 值均小于HTT-CNN的值，且HTT-ResNet的{\xi _{{\rm{test}}}} 值在多次实验下的波动性也小于HTT-CNN的值。图8和图9分别以代表性单峰火焰样本和双峰火焰样本在噪声比例为10%时的重建为例，比较了HTT-CNN和HTT-ResNet重建的燃烧场温度分布图像的质量。此外，为了与以RoI内温度分布为成像目标的经典重建算法进行比较，图8(b)显示了Landweber算法为单峰火焰样本重建的
{\rm{40}} \times {\rm{40}} 像素的RoI温度分布图像。由于Landweber算法为双峰火焰样本重建的RoI图像质量非常差，所以这里未展示该重建结果。由图8可见，与Landweber算法和HTT-CNN方案相比，HTT-ResNet方案重建的RoI更准确。由图8和图9可见，与HTT-CNN相比，HTT-ResNet方案不但能正确地确定出温度峰值的位置，而且其对整个燃烧场温度分布的还原能力更强。在其他噪声比例下进行的对比实验也得到了相同的结果。
5.3 实际测量数据重建实验
利用如图2所示的TDLAT系统的实际测量数据对本文提出的HTT-ResNet方案进行验证。以实验平台实际测得的
{\rm{4}} \times {\rm{8}} \times {\rm{2}} 个光谱吸收测量值为输入，利用Landweber算法重建RoI温度分布图像，并分别利用HTT-CNN和HTT-ResNet方案重建完整待测区域的温度分布图像。采用在0～25%噪声比例下训练出的HTT-CNN和HTT-ResNet分别进行对比实验。实验结果表明，在0～25%噪声比例下训练出的网络均能实现燃烧场温度分布图像的重建，且在10%～20%噪声比例下训练出的网络的重建效果更佳。图10与图11以在20%噪声比例下训练出的网络为例，分别展示了具有代表性的单火焰实验与双火焰实验的重建温度图像。由图10可见，对于实际火焰实验，HTT-ResNet方案重建的RoI质量高于Landweber算法和HTT-CNN方案。由图10和图11可见，与HTT-CNN相比，HTT-ResNet方案基于真实测量数据重建的燃烧场温度分布图像更能反映实际燃烧场的真实状态。在采用其他噪声比例下训练出的网络进行的重建实验中，HTT-ResNet方案的重建图像效果均优于HTT-CNN。
最后，表1以噪声比例为10%条件下的训练与测试为例，比较了HTT-ResNet与HTT-CNN的网络训练时间、测试样本平均重建时间和实际样本的平均重建时间。由表1可见，HTT-ResNet的训练时间与重建时间长于HTT-CNN。这主要是因为HTT-ResNet为了完整重建整个燃烧场的温度分布而增加了网络深度。在其他噪声比例下进行的对比实验也具有同样的时间相对关系。
表 1 HTT-ResNet与HTT-CNN训练时间和重建时间的对比重建算法 训练时间(min) 1090个测试样本的平均重建时间(s) 21个实际样本的平均重建时间(s) HTT-CNN 4.4 7.042×10–4 0.0248 HTT-ResNet 16.1 1.201×10–3 0.0461 6. 结束语
本文研究符合燃烧场实际气体分布与吸收特性的火焰参数场空间层次化离散模型，并在此基础上为TDLAT系统设计了一种基于残差网络的燃烧场层次化温度层析成像方案HTT-ResNet。该方案对计算资源与燃烧场不同空间区域的成像分辨率进行优化配置，在使重建结果符合燃烧场实际气体光谱吸收特性的同时，以高空间分辨率重点描述RoI内的温度分布。利用随机多模态高斯火焰模型进行的实验表明，在0～25%的噪声比例下，相对于现有的基于CNN的温度场重建算法，HTT-ResNet获得的测试集平均归一化重建误差降低了28.8%～64.3%。利用实际TDLAT系统测量数据进行的实验表明，HTT-ResNet重建的温度图像能够准确定位火焰的空间位置、清晰描述燃烧场的温度分布，是一种实用的温度场层析成像方案。层次化离散模型下的燃烧场温度与气体浓度基于深度学习的联合重建是下一步的研究目标。
-
表 1 HTT-ResNet与HTT-CNN训练时间和重建时间的对比
重建算法 训练时间(min) 1090个测试样本的平均重建时间(s) 21个实际样本的平均重建时间(s) HTT-CNN 4.4 7.042×10–4 0.0248 HTT-ResNet 16.1 1.201×10–3 0.0461 
下载: 导出CSV
-
[1] LIU Chang, CAO Zhang, LIN Yuzhen, et al. Online cross-sectional monitoring of a swirling flame using TDLAS tomography[J]. IEEE Transactions on Instrumentation and Measurement, 2018, 67(6): 1338–1348. doi: 10.1109/TIM.2018.2799098 [2] JANG H and CHOI D. Similarity analysis for time series-based 2D temperature measurement of engine exhaust gas in TDLAT[J]. Applied Sciences, 2020, 10(1): 285. doi: 10.3390/app10010285 [3] YU Tao and CAI Weiwei. Benchmark evaluation of inversion algorithms for tomographic absorption spectroscopy[J]. Applied Optics, 2017, 56(8): 2183–2194. doi: 10.1364/AO.56.002183 [4] CAI Weiwei and KAMINSKI C F. A numerical investigation of high-resolution multispectral absorption tomography for flow thermometry[J]. Applied Physics B, 2015, 119(1): 29–35. doi: 10.1007/s00340-015-6012-5 [5] 文成林, 吕菲亚. 基于深度学习的故障诊断方法综述[J]. 电子与信息学报, 2020, 42(1): 234–248. doi: 10.11999/JEIT190715WEN Chenglin and LV FeiYa. Review on deep learning based fault diagnosis[J]. Journal of Electronics &Information Technology, 2020, 42(1): 234–248. doi: 10.11999/JEIT190715 [6] HENDRIKSEN A A, PELT D M, PALENSTIJN W J, et al. On-the-fly machine learning for improving image resolution in tomography[J]. Applied Sciences, 2019, 9(12): 2445. doi: 10.3390/app9122445 [7] DAVOUDI N, DEÁN-BEN X L, and RAZANSKY D. Deep learning optoacoustic tomography with sparse data[J]. Nature Machine Intelligence, 2019, 1(10): 453–460. doi: 10.1038/s42256-019-0095-3 [8] RYU D, JO Y, YOO J, et al. Deep learning-enabled image quality control in tomographic reconstruction: Robust optical diffraction tomography[J]. Scientific Reports, 2019, 9: 15239. doi: 10.1038/s41598-019-51363-x [9] JIN Ying, ZHANG Wanqing, SONG Yang, et al. Three-dimensional rapid flame chemiluminescence tomography via deep learning[J]. Optics Express, 2019, 27(19): 27308–27334. doi: 10.1364/OE.27.027308 [10] YU Tao, CAI Weiwei, and LIU Yingzheng. Rapid tomographic reconstruction based on machine learning for time-resolved combustion diagnostics[J]. Review of Scientific Instruments, 2018, 89(4): 043101. doi: 10.1063/1.5016403 [11] HUANG Jianqing, LIU Hecong, DAI Jinghang, et al. Reconstruction for limited-data nonlinear tomographic absorption spectroscopy via deep learning[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2018, 218: 187–193. doi: 10.1016/j.jqsrt.2018.07.011 [12] HUANG Jianqing, ZHAO Jianan, and CAI Weiwei. Compressing convolutional neural networks using POD for the reconstruction of nonlinear tomographic absorption spectroscopy[J]. Computer Physics Communications, 2019, 241: 33–39. doi: 10.1016/j.cpc.2019.03.020 [13] 赵小强, 宋昭漾. 多级跳线连接的深度残差网络超分辨率重建[J]. 电子与信息学报, 2019, 41(10): 2501–2508. doi: 10.11999/JEIT190036ZHAO Xiaoqiang and SONG Zhaoyang. Super-resolution reconstruction of deep residual network with multi-level skip connections[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2501–2508. doi: 10.11999/JEIT190036 [14] BAO Yong, ZHANG Rui, ENEMALI G, et al. Relative entropy regularized TDLAS tomography for robust temperature imaging[J]. IEEE Transactions on Instrumentation and Measurement, 2020, 70: 4501909. doi: 10.1109/TIM.2020.3037950 期刊类型引用(3)
1. 司菁菁，王静波，程银波，刘畅. 基于双域多尺度特征融合的激光吸收光谱多分辨率温度层析成像. 中国激光. 2024(23): 132-144 . 
百度学术2. 司菁菁，王晓莉，程银波，刘畅. 基于级联视觉Transformer与多尺度特征融合的燃烧场温度层析成像. 电子与信息学报. 2023(10): 3511-3519 . 
本站查看3. 李金义，赵航，杨晓涛，赵烁. 激光吸收光谱2D和3D成像测量技术及其应用研究进展. 激光与光电子学进展. 2022(19): 71-84 . 百度学术其他类型引用(4)
-
下载:
百度学术
计量
- 文章访问数: 930
- HTML全文浏览量: 378
- PDF下载量: 71
- 被引次数: 7
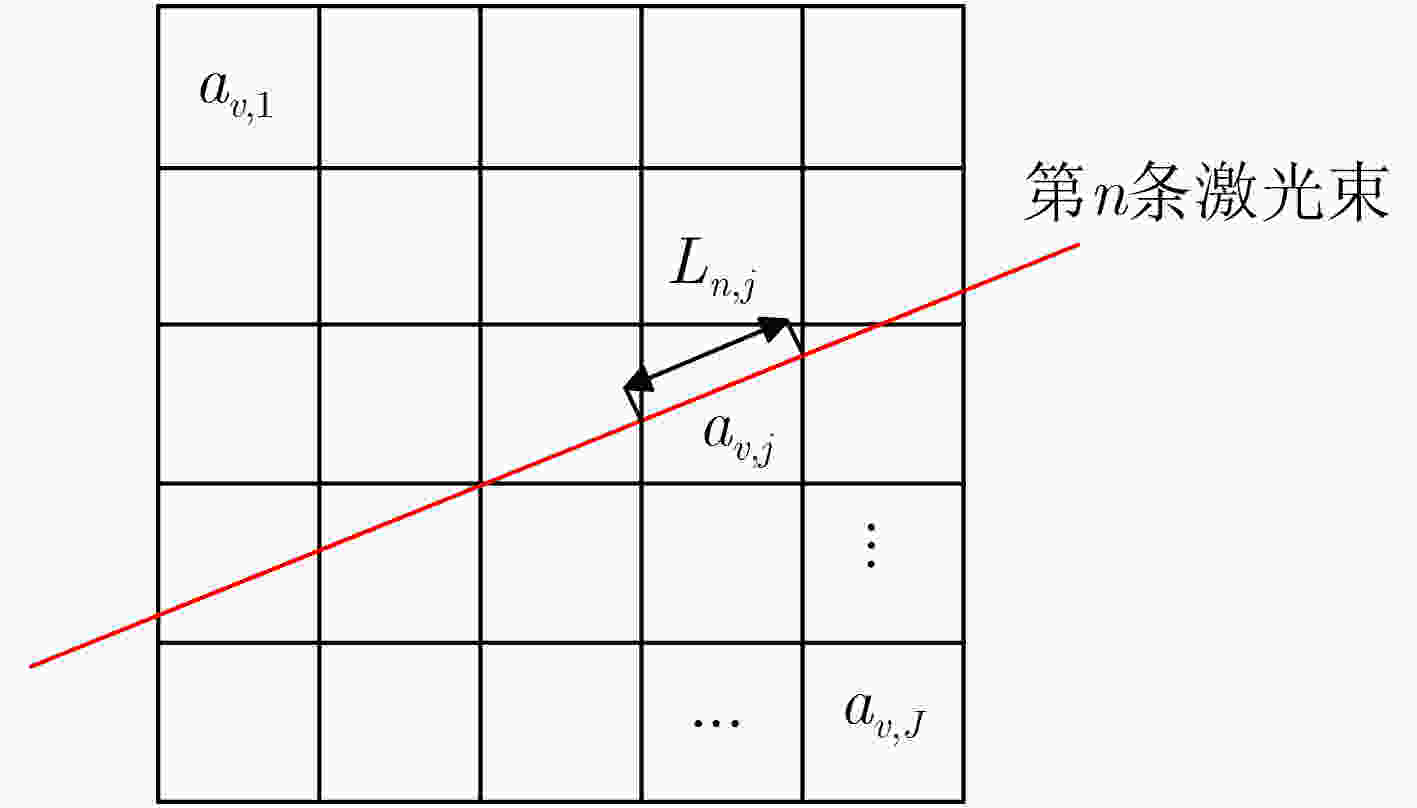
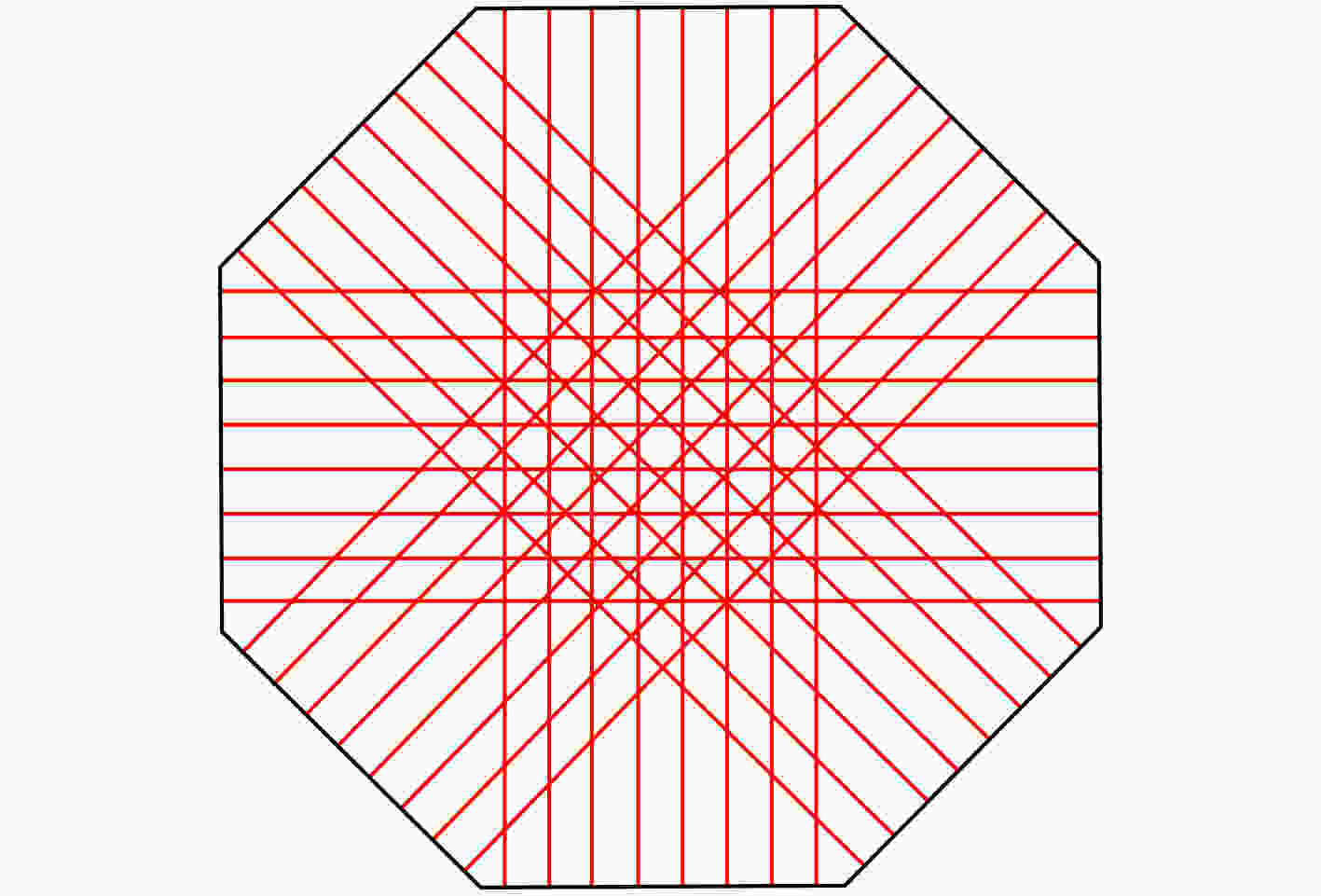
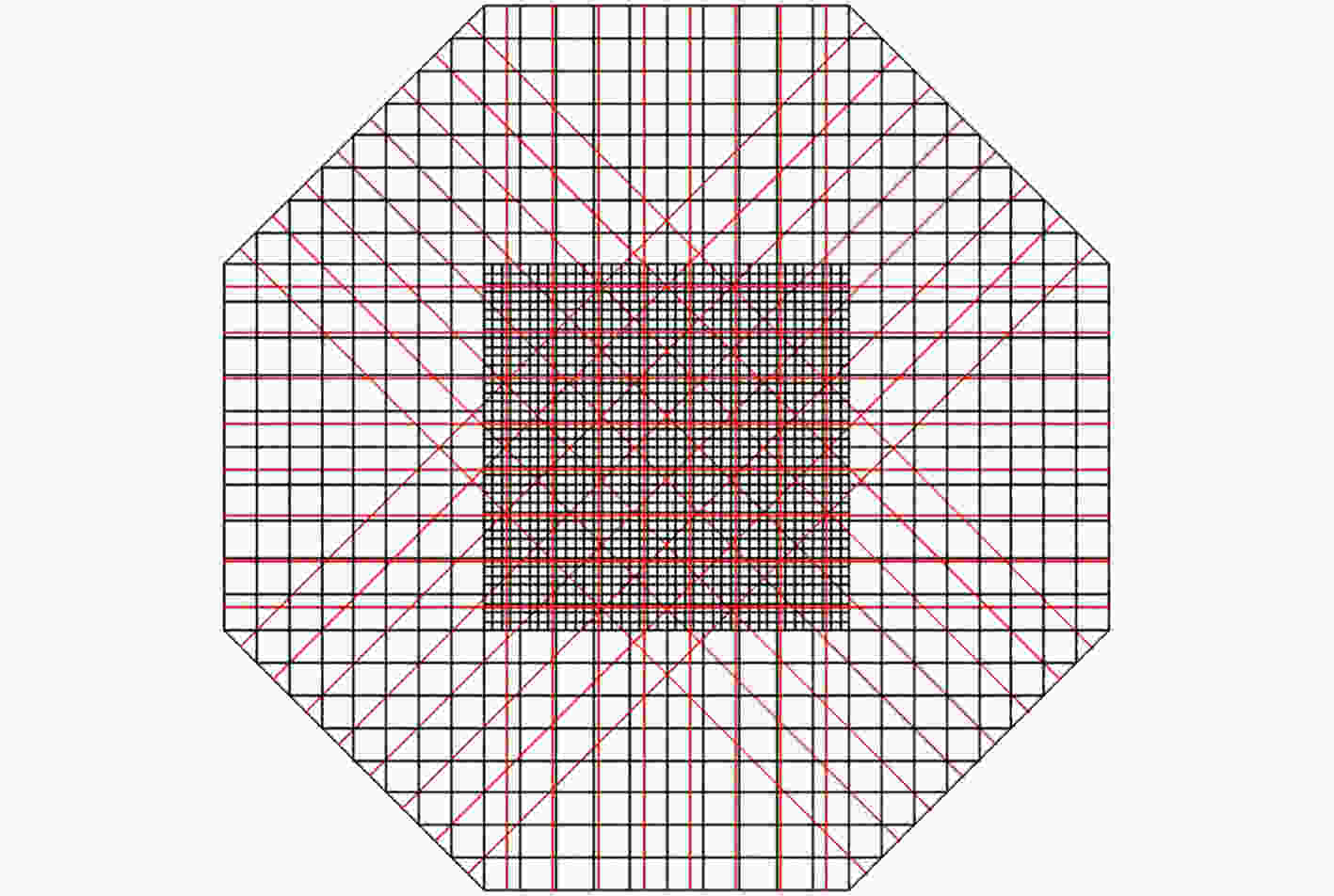
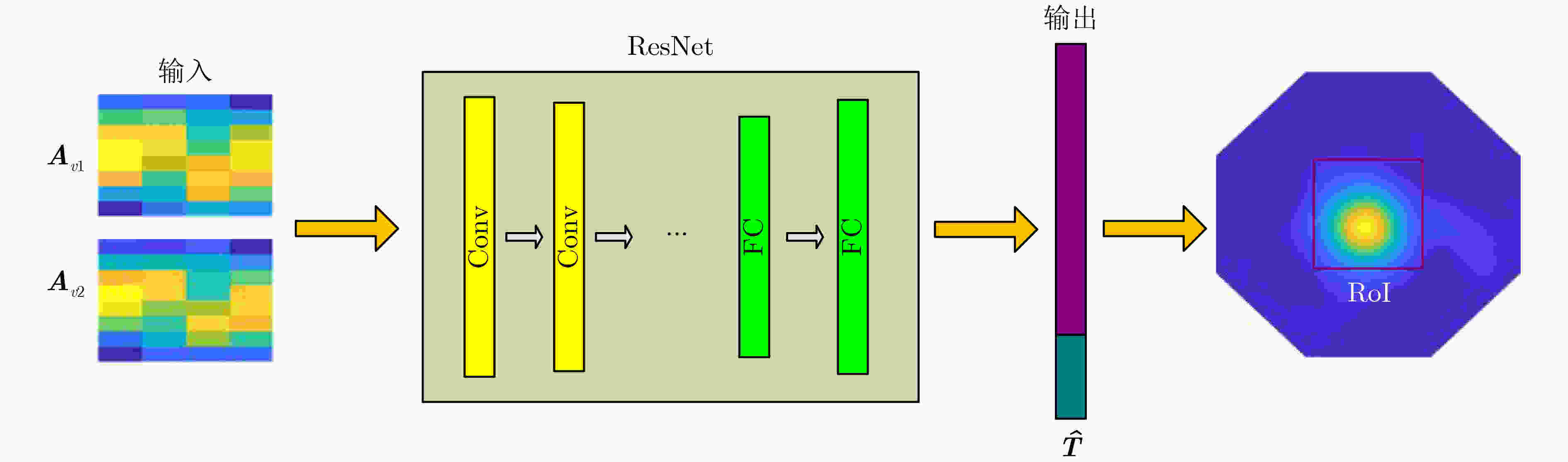
下载:
