Identity-based Public Key Keyword Searchable Encryption Scheme with Denial Authentication
-
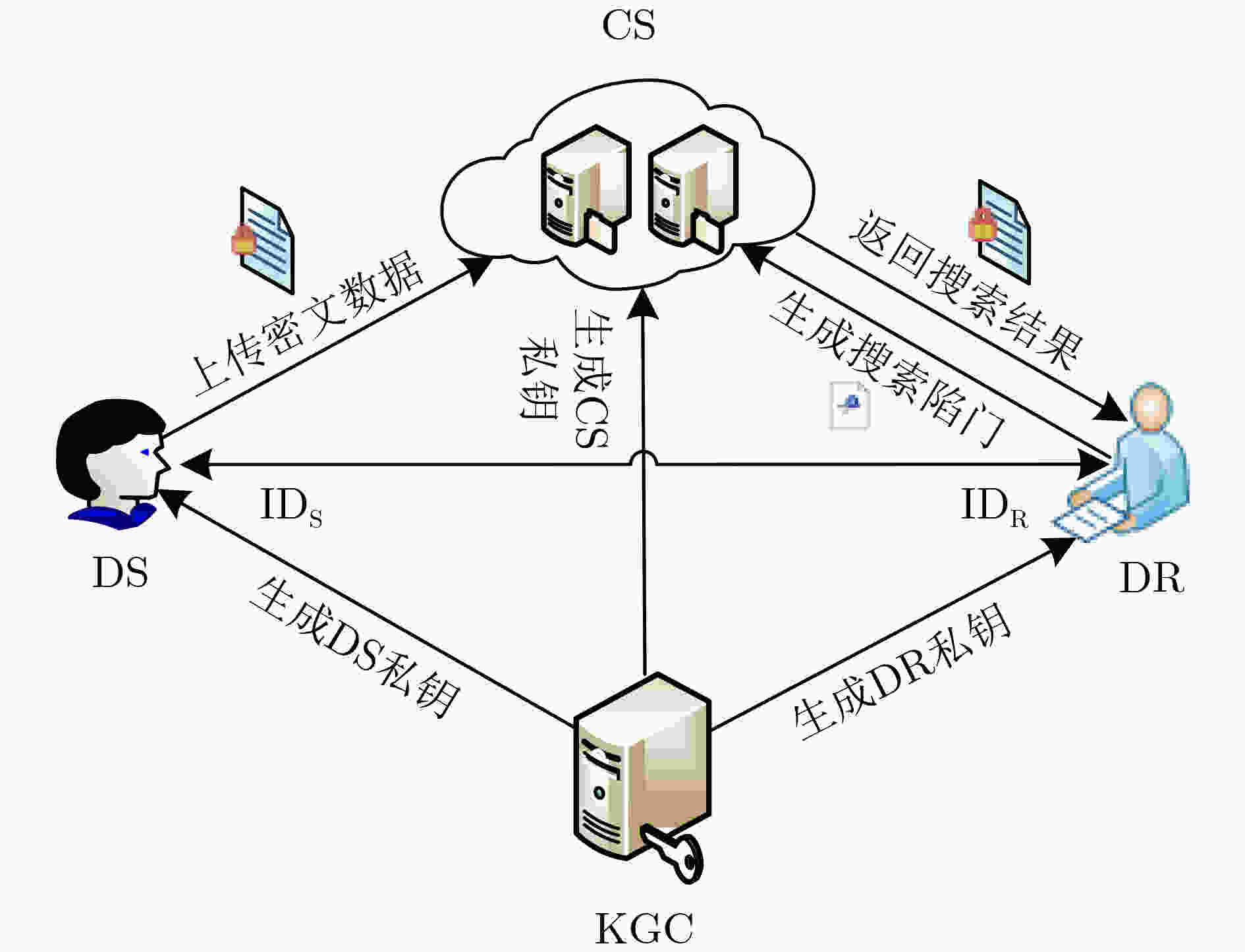
摘要: 云存储技术的发展实现了资源共享，为用户节省了数据管理开销。可搜索加密技术，既保护用户隐私又支持密文检索，方便了用户查找云端密文数据。现有的公钥关键字可搜索加密方案虽然支持身份认证，但未实现否认的属性。为了更好地保护发送者的身份隐私，该文将否认认证与公钥关键字可搜索加密技术相结合，提出一种基于身份的具有否认认证的关键字可搜索加密方案(IDAPKSE)。在该方案中，发送者上传密文后，能够对自己上传密文这一通信行为进行否认，与此同时，接收者可以确认密文数据的来源，但是，即使与第三方合作，接收者也不能向第三方证明其所掌握的事实。在随机预言模型下，基于双线性Diffie-Hellman(BDH)和决策双线性Diffie-Hellman(DBDH)数学困难问题，证明了该文方案满足不可伪造性、密文和陷门的不可区分性。Abstract: The development of cloud storage technology achieves resource sharing, which reduces users data management overhead. Searchable encryption technology protects users privacy and supports ciphertext retrieval, making it easy for users to find encrypted data in the cloud. Although existing public key searchable encryption schemes support authentication, the denial property is not implemented. To protect better the senders identity privacy, an Identity-based Public Key keyword Searchable Encryption scheme with Denial Authentication (IDAPKSE) is proposed. In the proposed scheme, the sender uploads the ciphertext and has the ability to deny that he or she uploaded the ciphertext to the cloud server. At the same time, the receiver can confirm the origin of the ciphertext, however, even with the cooperation of a third party, the receiver can not prove the facts in his/her possession to the third party. Under the random oracle model, based on the Bilinear Diffie-Hellman(BDH) and Decisional Bilinear Diffie-Hellman(DBDH) assumptions, the proposed scheme satisfies unforgeability of the ciphertexts, and indistinguishability of ciphertexts and trapdoors.
-
Key words:
- Privacy of identity /
- Denial of authentication /
- Searchable encryption
-
1. 引言
云存储技术[1]的发展实现了资源共享，帮助用户降低了存储成本。考虑到云端数据的敏感性，数据需要被加密后存放在云端，传统数据加密技术[2]虽有效地保护了数据的隐私，但同时又带来了对云端密文数据检索的难题。可搜索加密技术[3]在保护用户的隐私的同时又支持密文检索，在云存储中得到了广泛的应用。
2004年，
$ {\text{Boneh}} $ 等人[4]提出了第1个公钥可搜索加密方案(Public key Encryption with Keyword Search, PEKS)，该方案既支持密文检索又实现了数据共享，但搜索效率低，安全性较差。2006年，Byun等人[5]指出$ {\text{PEKS}} $ 方案存在离线关键字猜测攻击($ {\text{Keyword Guessing Attack}}{\kern 1pt} {\kern 1pt} {\text{,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{KGA}} $ )[6]的风险。传统的公钥可搜索加密方案需要证书颁发机构发布和管理用户的证书，基于身份密码体制[7]下的公钥可搜索加密方案解决了复杂的证书管理问题。2014年，Wu等人[8]在身份密码体制下提出了指定测试者的可搜索加密方案，该方案具有密文和陷门不可区分性，由于该方案并未完全定义在身份密码系统架构上，不能完全满足密文不可区分性。王少辉等人[9]在Wu等人方案基础上设计了一个具有更高效率可搜索加密方案，证明了密文不可区分性是抵御离线关键字猜测攻击的充分条件，故Wu等人方案也存在离线关键字猜测攻击的风险。2017年，$ {\text{Huang}} $ 等人[10]提出了具有公钥认证的可搜索加密方案，通过对关键字认证和加密，以抵御内部离线关键字猜测攻击。但该方案存在一个缺点，若云服务器被外部攻击者攻破，用户的搜索隐私将被泄露。为了保护用户的搜索隐私，
$ {\text{Baek}} $ 等人[11]提出在拥有陷门而没有接收者私钥的情况下，一个指定测试者无法完成云端密文数据的检索，但该方案无法抵御离线关键字猜测攻击。为了提高离线关键字猜测攻击下的安全性。2019年，$ {\text{Li}} $ 等人[12]提出了指定服务器的基于身份认证的关键字可搜索加密方案，$ {\text{Lu}} $ 等人[13]借鉴签密思想，实现了在关键字加密过程中，敌手不能试图通过产生合法关键字密文以达到匹配陷门的目的。普遍存在的缺陷是上述方案均没有考虑到对发送者身份隐私保护的问题。如今，个人信息和隐私趋于透明化。在电子投票、医疗信息、电子邮件、行政和司法报告等应用环境中，如何保护发送者的身份隐私，使其能够否认发送消息的行为已成为研究热点。否认认证协议由Dwork等人[14]首次提出，该协议基于零知识证明来定义，接收者可以确认消息发送者的身份，但无法向第三方证明这一事实。
$ {\text{Li}} $ 等人[15]在身份密码体制下提出了具有更高效率的否认认证加密方案，并在电子邮件系统中得到了很好的应用。$ {\text{Wu}} $ 等人[16]在身份密码体制下提出了同时具有认证性和否认性的否认认证加密方案。在基于身份的密码体制下，本文提出了具有否认属性的关键字可搜索加密方案，将否认认证与关键字可搜索加密技术相结合，在随机预言模型下，基于双线性Diffie-Hellman(Bilinear Diffie-Hellman, BDH)和决策双线性Diffie-Hellman(Decisional Bilinear Diffie-Hellman, DBDH)数学困难问题，证明了方案满足不可伪造性、密文和陷门不可区分性，同时具有否认性，即第三方无法确认消息的真实发送者，从而保护了发送者的身份隐私。
2. IDAPKSE安全模型
2.1 IDAPKSE系统模型
基于身份的具有否认认证的关键字可搜索加密方案(Identity-based Public Key keyword Searchable Encryption scheme with Denial Authentication, IDAPKSE)中有密钥分发中心、发送者、接收者和云服务器4类实体，系统模型图如图1所示。
(1) 密钥分发中心(Key Generation Center, KGC)：
$ {\text{KGC}} $ 生成系统参数$ {\text{params}} $ 和主密钥$ s $ ，并为发送者、接收者和云服务器提供私钥$ {\text{SK}}i $ 。(2) 发送者(Data Sender, DS)：
$ {\text{DS}} $ 对明文和所选关键字加密，将密文上传到云服务器。(3) 接收者(Data Receiver, DR)：
$ {\text{DR}} $ 运行陷门生成算法，将生成的陷门上传到云服务器。(4) 云服务器(Cloud Server, CS)：存储发送者上传的密文数据，并通过接收者上传的陷门，进行密文检索。
2.2 IDAPKSE形式化定义
IDAPKSE包括以下算法：
(1)
$ {\text{Setup}}{\kern 1pt} {\kern 1pt} (k) $ ：$ {\text{KGC}} $ 输入安全参数$ k $ ，返回系统参数$ {\text{params}} $ 和主密钥$ s $ 。(2) 密钥提取算法：(a)发送者和接收者密钥提取：
$ {\text{KGC}} $ 输入主密钥$ s $ 和身份标识$ {\text{ID}}i $ ，返回公私钥对$ {\text{(PK}}i{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{SK}}i) $ ；(b)云服务器密钥提取：$ {\text{KGC}} $ 输入系统参数$ {\text{params}} $ ，返回云服务器的公私钥对$({{{\rm{PK}}_{\rm{C}}}} {\text{,}} \; {{{\rm{SK}}_{\rm{C}}}})$ 。(3) 关键字否认认证加密算法：发送者输入参数
$ {\text{params}} $ 、关键字$ w $ 、发送者身份$ {{{\rm{ID}}_{\rm{S}}}} $ 和私钥$ {{{\rm{SK}}_{\rm{S}}}} $ 、云服务器的公钥$ {{{\rm{PK}}_{\rm{C}}}} $ 、接收者的身份$ {{{\rm{ID}}_{\rm{R}}}} $ 和公钥$ {{{\rm{PK}}_{\rm{R}}}} $ ，返回密文C并上传到云服务器。(4) 陷门生成算法：接收者输入系统参数
$ {\text{params}} $ 、关键字$ w $ 、发送者身份${{{\rm{ID}}_{\rm{S}}}}$ 和接收者身份${{{\rm{ID}}_{\rm{R}}}}$ ，输出陷门$T_w$ 。(5) 测试算法：云服务器输入系统参数
$ {\text{params}} $ 、服务器私钥${{{\rm{SK}}_{\rm{C}}}}$ 和陷门$T_w$ ，输出$ \phi $ 。若接收者上传的陷门与发送者上传的关键字密文中包含相同的关键字，则$ \phi = 1 $ ，否则$ \phi = 0 $ 。2.3 IDAPKSE安全模型
IDAPKSE方案的安全性主要考虑为不可伪造性、密文和陷门的不可区分性、否认性。下面通过挑战者
$ \beta $ 和敌手$\alpha_i{\kern 1pt} {\kern 1pt} (i = 1,2,3,4)$ 之间的游戏给出方案的安全模型。游戏 1 不可伪造性。
(1)
$ {\text{Setup}}{\kern 1pt} {\kern 1pt} (k) $ ：$ \beta $ 输入安全参数$ k $ ，返回系统参数$ {\text{params}} $ 给$\alpha_{\text{1}}$ ，自身保留主密钥$ s $ ，运行密钥提取算法，返回云服务器公私钥对$({{{\rm{PK}}_{\rm{C}}}} {\text{,}} \; {{{\rm{SK}}_{\rm{C}}}})$ 。(2) 私钥询问阶段：
$\alpha_{\text{1}}$ 对目标身份外的用户进行私钥询问，$ \beta $ 运行密钥提取算法返回私钥给$\alpha_{\text{1}}$ 。(3) 关键字否认认证加密询问阶段：
$\alpha_{\text{1}}$ 向$ \beta $ 提交发送者身份${{{\rm{ID}}_{\rm{S}}}}$ 、接收者身份${{{\rm{ID}}_{\rm{R}}}}$ 和关键字$ w $ 。$ \beta $ 运行密钥提取算法得到发送者的私钥${{{\rm{SK}}_{\rm{S}}}}$ ，运行关键字否认认证加密算法，返回密文$ C $ 给$\alpha_{\text{1}}$ 。(4) 陷门询问阶段：
$ \alpha_{\text{1}} $ 可以对挑战关键字外的任意关键字进行陷门询问。$ \beta $ 通过$ \alpha_{\text{1}} $ 选取的关键字$ w $ ，运行陷门生成算法生成陷门$T_w$ ，返回给$ \alpha_{\text{1}} $ 。(5) 伪造阶段：
$\alpha_{\text{1}}$ 输入$({w^ * },\;{\rm{PK}}_{\text{C}}^ *{\text{,}}\;{\rm{PK}}_{\text{S}}^ * {\text{,}}$ ${\text{PK}}_{\text{R}}^ * {\text{,}} $ $ \;{\text{ID}}_{\text{S}}^ * {\text{,}}\;{\text{ID}}_{\text{R}}^ * )$ ，生成${\text{ID}}_{\text{S}}^ *$ 和${\text{ID}}_{\text{R}}^ *$ 下的合法密文$ {C^ * } $ 。若$\alpha_{\text{1}}$ 未对${\text{ID}}_{\text{S}}^ *$ 和${\text{ID}}_{\text{R}}^ *$ 进行私钥询问，则在游戏1中获胜。游戏 2 密文不可区分性。
(1)
$ {\text{Setup}}{\kern 1pt} {\kern 1pt} (k) $ 、私钥询问阶段、关键字否认认证加密询问阶段和陷门询问阶段同游戏1。(2) 挑战阶段：
$\alpha_2$ 向$ \beta $ 提交发送者的身份${{{\rm{ID}}_{\rm{S}}}}$ 和接收者的身份${{{\rm{ID}}_{\rm{R}}}}$ 、挑战关键字$(w_0^*,\;w_1^*)$ 。$ \beta $ 随机选择$ b \in \{ 0{\kern 1pt} {\kern 1pt} ,1\} $ ，生成$w_b$ 密文$ {C^ * } $ 返回给$\alpha_2$ 。(3)
$\alpha_2$ 继续执行以上的询问。(4) 猜测阶段：
$\alpha_2$ 输出$ b' \in \{ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} 1\} $ ，若$ b' = b $ ，$\alpha_2$ 未对${\text{ID}}_{\text{S}}^ *$ 和${\text{ID}}_{\text{R}}^*$ 进行私钥询问且未对$(w_0^* ,\;w_1^*)$ 进行关键字否认认证加密询问，则在游戏2中获胜。$\alpha_2$ 赢得游戏2的优势为$$ {\text{Adv}}{{\kern 1pt} _{\alpha_2}}{\kern 1pt} (k) = {\kern 1pt} {\kern 1pt} |\Pr {\kern 1pt} {\kern 1pt} [b' = b] - 1/2| $$ (1) 游戏 3 陷门不可区分性。
(1)
$ {\text{Setup}}{\kern 1pt} {\kern 1pt} (k) $ ：私钥询问阶段、关键字否认认证加密询问阶段和陷门询问阶段同游戏1。(2) 挑战阶段：
$\alpha_3$ 向$ \beta $ 提交发送者的身份${{{\rm{ID}}_{\rm{S}}}}$ 和接收者的身份${{{\rm{ID}}_{\rm{R}}}}$ 、挑战关键字$(w_0^ *,\;w_1^ * )$ 。$ \beta $ 随机选择$ b \in \{ 0{\kern 1pt} {\kern 1pt} ,1\} $ ，生成$w_b$ 的陷门$T_w^ *$ 返回给$\alpha_3$ 。(3)
$\alpha_3$ 继续执行以上的询问。(4) 猜测阶段：
$\alpha_3$ 输出$b' \in \{ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} 1\}$ ，若$ b' = b $ ，$\alpha_3$ 未对${\text{ID}}_{\text{S}}^ *$ 和${\text{ID}}_{\text{R}}^ *$ 进行私钥询问且未对关键字$(w_0^ * ,\;w_1^ * )$ 进行关键字否认认证加密和陷门询问，则在游戏3中获胜。$\alpha_3$ 赢得游戏3的优势为$$ {\text{Adv}}{{\kern 1pt} _{\alpha_3}}{\kern 1pt} (k) = {\kern 1pt} {\kern 1pt} |\Pr {\kern 1pt} [b' = b] - 1/2| $$ (2) 游戏 4 否认性。
(1)
$ {\text{Setup}}{\kern 1pt} {\kern 1pt} (k) $ ：假设$ \beta $ 能够为系统中的任何诚实用户生成IDAPKSE方案下的合法密文，选择两个诚实的用户$D_{\text{0}}$ 和$D_{\text{1}}$ 。(2) 挑战阶段：
$\alpha_4$ 向$ \beta $ 提交明文消息$ M $ ，$ \beta $ 随机选择$ b \in \{ 0{\kern 1pt} {\kern 1pt} ,1\} $ ，并与$D_{\text{b}}$ 交互，使$D_{\text{b}}$ 能够将$ M $ 生成IDAPKSE方案下的合法密文$ {C^ * } $ 返回给$\alpha_4$ 。(3) 区分阶段：
$\alpha_4$ 输出$ b' \in \{ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} 1\} $ ，若$ b' = b $ ，则$\alpha_4$ 在游戏4中获胜。因游戏中
$D_{\text{0}}$ 和$D_{\text{1}}$ 生成的密文的概率分布是相同的，所以对于区分者是不可区分的。$\alpha_4$ 赢得游戏4的优势为$$ {\text{Adv}}{{\kern 1pt} _{\alpha_4}}{\kern 1pt} (k) = {\kern 1pt} {\kern 1pt} |\Pr {\kern 1pt} {\kern 1pt} [b' = b] - 1/2| $$ (3) 3. IDAPKSE方案
3.1 具体方案
(1)
$ {\text{Setup}}{\kern 1pt} {\kern 1pt} (k) $ ：输入安全参数$ k $ ，$ {\text{KGC}} $ 执行以下操作：(a)选择$ q $ 阶循环群$ G_1 $ 和$G_2$ ，$ g $ 为$ G_1 $ 的生成元，再选择双线性映射$ e:G_1 \times G_1 \to G_2 $ ；(b)在$ G_1 $ 群中选择生成元$ U $ 和$ h $ ，$ {\text{KGC}} $ 随机选择$s \in Z_q^ *$ 作为主密钥，并计算公钥$P_{\text{pub}} = {\kern 1pt} sU$ ；(c)定义3个抗碰撞的哈希函数：$H_1:{\{ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} 1\} ^ * } \to G_1$ ；$H_2:G_2 \times \{ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} , $ $ {\kern 1pt} {\kern 1pt} {\kern 1pt} 1\} ^ * \to G_1$ ；$H_{\text{3}}:{\{ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} 1\} ^ * } \to Z_q^ *$ 。$ {\text{KGC}} $ 保留主密钥$ s $ ，公开系统参数${\text{params}} = \{ k{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} q{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} G_1{\kern 1pt} {\kern 1pt} ,\;G_2{\kern 1pt} {\kern 1pt} {\kern 1pt} , \;U,\;h{\kern 1pt} {\kern 1pt} , \;g{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\; $ $ P_{\text{pub}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\;H_1{\kern 1pt} {\kern 1pt} {\kern 1pt} , \;H_2{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\;H_3\}$ 。(2) 密钥提取算法：(a)发送者和接收者密钥提取：发送者和接收者将身份
$ {\text{ID}}i $ 发送给$ {\text{KGC}} $ ，$ {\text{KGC}} $ 计算对应公钥$Q_i\; = \;H_1{\text{(ID}}i{\text{)}}$ 和私钥${\text{SK}}_i\; = \;sQ_i$ ，并通过安全信道将私钥返回给发送者和接收者；(b)云服务器密钥提取：$ {\text{KGC}} $ 随机选择$t \in Z_q^ *$ 作为云服务器私钥；输入$ t $ 和系统参数$ {\text{params}} $ ，计算云服务器公钥${{{\rm{PK}}_{\rm{C}}}} = tg$ 。(3) 关键字否认认证加密算法：发送者输入系统参数
$ {\text{params}} $ 、关键字$ w $ 、发送者身份${{{\rm{ID}}_{\rm{S}}}}$ 和公私钥对$({{{\rm{PK}}_{\rm{S}}}} {\text{,}}\; {{{\rm{SK}}_{\rm{S}}}})$ 、接收者身份${\text{ID}}_{\text{R}}$ 和公钥${{{\rm{PK}}_{\rm{R}}}}$ 、云服务器公钥${{{\rm{PK}}_{\rm{C}}}}$ ，按以下步骤加密关键字：(a)计算：
$Q_{\text{S}} = H_1{\text{(IDs)}}$ ,$Q_{\text{R}} = H_1{{({\rm{ID}}_{\rm{R}})}}$ ,$T = $ $ rQ_{\text{S}}$ ，其中$r \in Z_q^ *$ ；(b)计算：
$C_1 = e{\kern 1pt} {\kern 1pt} {(H_2\;(Z{\kern 1pt} {\kern 1pt} {\text{,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} w)\;,\;{{{\rm{PK}}_{\rm{C}}}})^r}$ ，其中$Z = e{\kern 1pt} {\kern 1pt} ({{{\rm{SK}}_{\rm{S}}}}\;{\text{,}}\;Q_{\text{R}})$ ；(c)计算：
$C_{\text{2}} = rg$ ,$C_{\text{3}} = rh$ ；(d)计算：
$Y = H_3\;(w||{{{\rm{ID}}_{\rm{R}}}}||{{{\rm{ID}}_{\rm{S}}}}\;,\;T)$ ；(e)计算：
$V = e{\kern 1pt} {\kern 1pt} ((r + Y){\kern 1pt} {\kern 1pt} {{{\rm{SK}}_{\rm{S}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} Q_{\text{R}})$ ；(f)
$C{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = (T{\kern 1pt} ,\;C_1{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\;C_2{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\;C_3{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\;V{\kern 1pt} {\kern 1pt} )$ ，将$ C $ 上传到云服务器。(4) 陷门生成算法：接收者输入系统参数
$ {\text{params}} $ 、关键字$ w $ 、发送者公钥${{{\rm{PK}}_{\rm{S}}}}$ 和接收者私钥${{{\rm{SK}}_{\rm{R}}}}$ , 按下步骤生成关键字陷门：(a)计算：
$Z' = e\;(H_1\;({{{\rm{ID}}_{\rm{S}}}})\;{\text{,}}\;{{{\rm{SK}}_{\rm{R}}}})$ ；(b)计算：
$T_1 = ag$ ，$T_2 = H_2\;(Z'{\kern 1pt} ,\;w) + ah$ ，其中$a \in Z_q^*$ ，将陷门$T_w = (T_1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} T_2)$ 上传到云服务器。(5) 测试算法：云服务器运行该算法，验证等式
$C_1 \cdot e\;({{{\rm{SK}}_{\rm{C}}}}T_1\;,\;C_3) = e\;({{{\rm{SK}}_{\rm{C}}}}T_2\;,\;C_2)$ 是否成立，若成立，说明关键字密文与陷门相匹配，返回1，否则返回0。(6) 解密算法：若关键字密文与陷门相匹配，云服务器将关键字密文
$ C $ 发送给接收者，接收者利用自身私钥${{{\rm{SK}}_{\rm{R}}}}$ 在本地执行解密操作。3.2 IDAPKSE方案正确性分析
IDAPKSE方案的正确性当且仅当验证等式
$C_1 \cdot e\;({{{\rm{SK}}_{\rm{C}}}}T_1\;,\;C_3) = e\;({{{\rm{SK}}_{\rm{C}}}}T_2\;,\;C_2)$ 是否成立$$ \begin{split} e{\kern 1pt} {\kern 1pt} ({{{\rm{SK}}_{\rm{C}}}}T_2\;,\;C_2) & = e{\kern 1pt} {\kern 1pt} (t{\kern 1pt} {\kern 1pt} (H_2\;(Z',\;w) + ah),\;rg)\\ & = e{\kern 1pt} {\kern 1pt} (tH_2\;(Z',\;w),\;rg) \cdot e{\kern 1pt} {\kern 1pt} (tah{\kern 1pt} {\kern 1pt} ,\;rg) \\ & = e{\kern 1pt} {\kern 1pt} {(H_2\;(Z',\;w),\;tg)^r} \cdot e{\kern 1pt} {\kern 1pt} {\kern 1pt} (tag\;,\;rh) \\ & = e{\kern 1pt} {\kern 1pt} {(H_2\;(Z\;,\;w),\;tg)^r} \cdot \;e{\kern 1pt} {\kern 1pt} (tag\;,\;rh) \\ & = e{\kern 1pt} {\kern 1pt} {\kern 1pt} {(H_2\;(Z,\;w),\;{{{\rm{PK}}_{\rm{C}}}})^r} \cdot \;e{\kern 1pt} {\kern 1pt} {\kern 1pt} (tag\;,\;rh) \\ & = C_1\; \cdot \;e{\kern 1pt} {\kern 1pt} {\kern 1pt} ({{{\rm{SK}}_{\rm{C}}}}{\kern 1pt} T_1{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\;C_3)\\[-10pt] \end{split} $$ (4) 因为
$$ \begin{split} Z'\; &= e{\kern 1pt} {\kern 1pt} (H_1\;({{{\rm{ID}}_{\rm{S}}}}),\;{{{\rm{SK}}_{\rm{R}}}})\\ &= e{\kern 1pt} {\kern 1pt} {\kern 1pt} (H_1\;({{{\rm{ID}}_{\rm{S}}}})\;,\;sH_1\;({{{\rm{ID}}_{\rm{R}}}})) \\ &= e{\kern 1pt} {\kern 1pt} (sH_1\;({{{\rm{ID}}_{\rm{S}}}})\;,\;H_1\;({{{\rm{ID}}_{\rm{R}}}})) \\ &= \;e{\kern 1pt} {\kern 1pt} ({{{\rm{SK}}_{\rm{S}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{,}}\;Q_{\text{R}}) \\ &= Z \end{split} $$ (5) 所以
$ C_1 \cdot e{\kern 1pt} {\kern 1pt} ({{{\rm{SK}}_{\rm{C}}}}T_1\;,\;C_3) = e{\kern 1pt} {\kern 1pt} ({{{\rm{SK}}_{\rm{C}}}}T_2\;,\;C_2) $ 成立。4. 安全性分析
4.1 不可伪造性
引理1 在随机预言模型下，若敌手
$\alpha_{\text{1}}$ 在时间$ t $ 内赢得游戏1，则存在算法$ \mathbb{C} $ 可以解决$ {\text{BDH}} $ 问题。证明 挑战者
$ \beta $ 输入1个随机的$ {\text{BDH}} $ 问题实例$ (P{\kern 1pt} {\kern 1pt} ,\;aP{\kern 1pt} {\kern 1pt} ,\;bP{\kern 1pt} {\kern 1pt} ,\;cP) $ ，目标计算$ e{\kern 1pt} {\kern 1pt} {(P{\kern 1pt} {\kern 1pt} ,\;P)^{abc}} $ 。(1)
$ {\text{Setup}}{\kern 1pt} {\kern 1pt} (k) $ ：$ \beta $ 输入安全参数$ k $ ，返回系统参数$ {\text{params}} $ 给$\alpha_{\text{1}}$ 。设置公钥$P_{\text{pub}}\; = cP$ ，$ c $ 为主密钥。(2) 攻击阶段：
$ \beta $ 维护$L_1\;,L_2\;,L_3$ 列表，将其初始化为空，分别作为$\alpha_{\text{1}}$ 对随机预言机$H_1\;,H_2\;,H_3$ 的查询追踪，$\alpha_{\text{1}}$ 执行多项式有界次查询：(a)公钥询问：
$\alpha_{\text{1}}$ 向$ \beta $ 提交任意用户身份$ {\text{ID}}i $ ，$ \beta $ 检查$L_1$ 。若未对
$ {\text{ID}}i $ 进行任何询问，$ {\text{ID}}i $ 为$ \bot $ ，$ \beta $ 得到${\text{(ID}}i{\kern 1pt} {\kern 1pt} ,n_i)$ ，随机选择$x_i \in Z_q^ *$ 作为私钥${\text{SK}}i$ ，计算公钥${\text{PK}}i = x_iP$ ，返回$ {\text{PK}}i $ 给$\alpha_{\text{1}}$ 并向列表$L_1$ 中添加一个新的元组${\text{(ID}}i{\kern 1pt} {\kern 1pt} ,\;{\text{PK}}i{\kern 1pt} {\kern 1pt} ,\;{\text{SK}}i{\kern 1pt} {\kern 1pt} ,\;n_i)$ 。若
$ {\text{ID}}i $ 不为$ \bot $ ，$L_1$ 列表中存在相应的元组，则返回存在的结果。(b)私钥询问：
$\alpha_{\text{1}}$ 提交用户身份$ {\text{ID}}i $ ，获取相应的用户私钥，若${\text{ID}}i = {{{\rm{ID}}_{\rm{S}}}}$ 或${\text{ID}}i = {{{\rm{ID}}_{\rm{R}}}}$ ，结束模拟。否则，$ \beta $ 检查列表$L_1$ 。若未对
$ {\text{ID}}i $ 进行任何询问，$ {\text{ID}}i $ 为$ \bot $ ，$ \beta $ 得到${\text{(ID}}i{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} n_i)$ ，随机选择$x_i \in Z_q^ *$ 作为私钥$ {\text{SK}}i $ ，计算公钥${\text{PK}}i = \;x_i{\kern 1pt} P$ ，返回${\text{SK}}i$ 给$\alpha_{\text{1}}$ ，并向列表$L_1$ 中添加一个新的元组${\text{(ID}}i{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{PK}}i{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\;{\text{SK}}i{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} n_i)$ 。若
$ {\text{ID}}i $ 不为$ \bot $ ，$L_1$ 列表中存在相应的元组，则返回存在的结果。(c)关键字否认认证加密询问：
$\alpha_{\text{1}}$ 向$ \beta $ 提交选定的发送者身份${{{\rm{ID}}_{\rm{S}}}}$ 和接收者身份${\rm{ID}}_{\rm{R}}$ 及关键字$ w $ ,$ \beta $ 执行以下操作：若
$\alpha_{\text{1}}$ 提交的$ {\text{ID}}i $ 与$ \beta $ 选择的两个身份不同，即${\text{ID}}i\; \ne {{{\rm{ID}}_{\rm{S}}}}$ 和${\text{ID}}i\; \ne {{{\rm{ID}}_{\rm{R}}}}$ 。$ \beta $ 运行密钥提取算法得到发送者私钥${{{\rm{SK}}_{\rm{S}}}}$ ，运行关键字否认认证加密算法生成密文$ C $ 返回给$\alpha_{\text{1}}$ 。若
$\alpha_{\text{1}}$ 提交发送者身份$ {\text{ID}}i $ 是$ \beta $ 选择的两个身份之一，即${\text{ID}}i\; = {{{\rm{ID}}_{\rm{S}}}}$ 或${\text{ID}}i\; = {{{\rm{ID}}_{\rm{R}}}}$ ，但接收者身份${\text{ID}}_j \ne {{{\rm{ID}}_{\rm{S}}}}$ 且${\text{ID}}_j \ne \;{{{\rm{ID}}_{\rm{R}}}}$ 。$ \beta $ 不能计算发送者的私钥，但能计算接收者的私钥${\text{SK}}_j = n_jP_{\text{pub}}$ 。$ \beta $ 随机选择$r \in Z_q^ *$ ，进行以下计算：(a)计算：
$T = rQ_i$ ,$C_1 = e{\kern 1pt} {\kern 1pt} (H_2\;(e{\kern 1pt} {\kern 1pt} (T{\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{SK}}_j){\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} w){\kern 1pt} {\kern 1pt} {\kern 1pt} , $ $ {\kern 1pt} {\kern 1pt} {\kern 1pt} {{{\rm{PK}}_{\rm{C}}}})^r$ ；(b)计算：
$C_{\text{2}} = rg$ ,$C_3 = rh$ ；(c)计算：
$Y = H_3\;(w||{\text{ID}}i||{\text{ID}}_j{\kern 1pt} {\kern 1pt} ,\;T)$ ；(d)计算：
$V = e{\kern 1pt} {\kern 1pt} (T + YQi)\;,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{SK}}_j)$ ；(e)
$C = (T{\kern 1pt} ,\;C_1{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\;C_2{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\;C_3{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\;V{\kern 1pt} {\kern 1pt} )$ ，返回密文$ C $ 给$\alpha_{\text{1}}$ 。若
$\alpha_{\text{1}}$ 提交发送者身份与$ \beta $ 选中身份相同，即${\text{ID}}i\; = {{{\rm{ID}}_{\rm{S}}}}$ 且${\text{ID}}_j = \;{{{\rm{ID}}_{\rm{R}}}}$ 或${\text{ID}}_j = {{{\rm{ID}}_{\rm{S}}}}$ 且${\text{ID}}i\; = {{{\rm{ID}}_{\rm{R}}}}$ 。这时，$ \beta $ 不能够计算发送者和接收者的私钥，$ \beta $ 随机选择$r{\text{,}}{\kern 1pt} {\kern 1pt} h \in Z_q^*$ ，进行以下计算：(a)计算：
$T = rP - hQi\;$ ,$Y = H_3\;(w||{{{\rm{ID}}_{\rm{R}}}}||{{{\rm{ID}}_{\rm{S}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} , $ $ \;T)$ ，向列表$L_3$ 中添加元组$(w||{{{\rm{ID}}_{\rm{R}}}}||{{{\rm{ID}}_{\rm{S}}}}\;,\;T,\;h)$ ；(b)计算：
$C_1 = e{\kern 1pt} {\kern 1pt} {(H_2{\kern 1pt} {\kern 1pt} (e{\kern 1pt} {\kern 1pt} ({{{\rm{SK}}_{\rm{S}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ,Q_{\text{R}}),w){\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {{{\rm{PK}}_C}})^r}$ ，向列表$L_2\;$ 中添加元组${\text{(}}{\kern 1pt} {\kern 1pt} {{{\rm{PK}}_{\rm{S}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{,}}\;{{{\rm{PK}}_{\rm{R}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{,}}\;C_1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{,}}{\kern 1pt} {\kern 1pt} {\kern 1pt} V{\kern 1pt} {\kern 1pt} )$ ，其中$V = e((r + Y){\kern 1pt} {\kern 1pt} {{{\rm{SK}}_{\rm{S}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} Q_{\text{R}})$ ；(c)
$C = (T{\kern 1pt} ,\;C_1{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\;C_2{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\;C_3{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\;V)$ ，返回密文$ C $ 给$\alpha_{\text{1}}$ 。(d)伪造阶段：
$\alpha_1$ 输出发送者身份${{{\rm{ID}}_{\rm{R}}}}$ 、接收者身份${{{\rm{ID}}_{\rm{S}}}}$ 和密文$C{{\kern 1pt} ^ * } = (T{{\kern 1pt} ^ * },\;C_1^ * ,\;C_2^ * ,\;C_3^ * ,\;V{{\kern 1pt} ^ * })$ 。其中，$\alpha_{\text{1}}$ 未对${{{\rm{ID}}_{\rm{S}}}}$ 和${{{\rm{ID}}_{\rm{R}}}}$ 进行私钥询问，不确定$ {C^ * } $ 是否为有效密文。由分叉引理[17] 知，如果$ \alpha_{\text{1}} $ 为上述游戏中的一个成功的伪造者，那么可以构造$\alpha_{\text{1}}^ *$ ，$\alpha_{\text{1}}^ *$ 能够生成具有相同部分密文$ {T^ * } $ 的元组$({{{\rm{ID}}_{\rm{R}}}}\;,\;{{{\rm{ID}}_{\rm{S}}}}\;, $ $ \;{C^ * },\;C_1^ * ,C_2^ * ,\;C_3^ * ,\;{Y^ * },\;{V^ * })$ 和$({{{\rm{ID}}_{\rm{R}}}}\;,\;{{{\rm{ID}}_{\rm{S}}}}\;,\;{C^ * },\;C_1^ * , C_2^ * , $ $ \;C_3^ * ,\;Y_1^ * ,\;V_1^ * )$ ，其中$ Y_1^ * \ne \;{Y^ * } $ 。目前没有公认的解决
$ {\text{BDH}} $ 困难问题的有效算法，因此$\alpha_{\text{1}}$ 不存在，方案满足密文的不可伪造性。证毕4.2 密文不可区分性
引理2 在随机预言模型下，若敌手
$\alpha_{\text{2}}$ 在时间$ t $ 内赢得游戏2，则有算法$ \mathbb{C} $ 可以解决$ {\text{DBDH}} $ 问题。证明 挑战者
$ \beta $ 输入一个随机的$ {\text{DBDH}} $ 问题实例$(G_1{\kern 1pt} {\kern 1pt} ,\;G_2\;,\;e{\kern 1pt} {\kern 1pt} ,\;q{\kern 1pt} {\kern 1pt} ,g{\kern 1pt} {\kern 1pt} ,\;xg{\kern 1pt} {\kern 1pt} ,\;yg{\kern 1pt} {\kern 1pt} ,\;zg{\kern 1pt} {\kern 1pt} ,\;Z)$ ，目标是解决$ {\text{DBDH}} $ 问题。(1)
$ {\text{Setup}}(k) $ ：$ \beta $ 输入安全参数$k$ ，返回${\text{params}} = \{ k{\kern 1pt} {\kern 1pt} ,\;q{\kern 1pt} {\kern 1pt} ,\;G_1{\kern 1pt} {\kern 1pt} ,\;G_2\;,\;e{\kern 1pt} {\kern 1pt} ,\;P,{\kern 1pt} {\kern 1pt} {\kern 1pt} h{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} g{\kern 1pt} {\kern 1pt} {\kern 1pt} ,P_{\text{pub}}\;\}$ ，其中$P_{\text{pub}} = ZP$ ，$ Z $ 为主密钥。计算云服务器公私钥对${{{\rm{PK}}_{\rm{C}}}}\; = \;tg$ 和${{{\rm{SK}}_{\rm{C}}}}\; = \;t$ ，将$ {\text{params}} $ 和云服务器公私钥对$({{{\rm{PK}}_{\rm{C}}}}\;{\text{,}}\;{{{\rm{SK}}_{\rm{C}}}})$ 返回给$\alpha_2$ 。(2) 攻击阶段：
$ \beta $ 维护$L_1\;,L_2\;,L_3$ 列表，将其初始化为空，分别作为$\alpha_2$ 对随机预言机$H_1{\kern 1pt} {\kern 1pt} ,H_2{\kern 1pt} {\kern 1pt} ,H_3$ 的查询追踪，$\alpha_2$ 执行多项式有界次查询：(a)公钥询问，私钥询问和关键字否认认证加密询问同上文不可伪造性证明。
(b)陷门询问阶段：
$\alpha_2$ 向$ \beta $ 提交选择的发送者身份${{{\rm{ID}}_{\rm{S}}}}$ 、接收者身份${{{\rm{ID}}_{\rm{R}}}}$ 和关键字$ w $ ，$ \beta $ 执行以下操作：若
$\alpha_2$ 提交的发送者的身份与$ \beta $ 选取的身份相同，即${\text{ID}}i\; = {{{\rm{ID}}_{\rm{S}}}}$ 且${\text{ID}}j = \;{{{\rm{ID}}_{\rm{R}}}}$ 或${\text{ID}}i\; = {{{\rm{ID}}_{\rm{R}}}}$ 且${\text{ID}}j = $ $ {{{\rm{ID}}_{\rm{S}}}}$ ，计算$T_1 = ag$ ,$T_2 = H_2\;(Z{\kern 1pt} {\kern 1pt} ,\;w) + ah$ ，返回陷门$T_w = (T_1\;{\kern 1pt} ,\;T_2)$ 给$\alpha_2$ 。若
$\alpha_2$ 提交的发送者的身份$ {\text{ID}}i $ 最多与$ \beta $ 选择的两个身份中的一个相同，则计算$T_1 = ag$ ,$T_2 = H_2 $ $ {\kern 1pt} {\kern 1pt} (Zg\;,\;w) + ah$ ，返回陷门$T_w = (T_1\;,{\kern 1pt} {\kern 1pt} {\kern 1pt} T_2)$ 给$\alpha_2$ 。(3) 挑战阶段：
$\alpha_2$ 输出两个挑战关键词$(w_0^ * ,\;w_1^ * )$ 、发送者身份${{{\rm{ID}}_{\rm{S}}}}$ 和接收者身份${{{\rm{ID}}_{\rm{R}}}}$ 。$ \beta $ 随机选取$ b \in \{ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} 1\} $ ，随机选择$r \in Z_q^ *$ ，返回密文$C{{\kern 1pt} ^ * } = (T{{\kern 1pt} ^ * },\;C_1^ * ,\;C_2^ * ,\;C_3^ * ,\;V{^ * })$ 给$\alpha_2$ 。(4)
$\alpha_2$ 继续执行上询问。(5) 猜测阶段：
$\alpha_2$ 输出$ b' \in \{ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} 1\} $ ，若$ b' = b $ ，输出$ 1 $ ，否则输出$ 0 $ 。$\overline F $ 表示对挑战身份的猜测是不正确的，挑战者$ \beta $ 将中止。若
$ \beta $ 中止，则$ \beta $ 随机输出$ b $ 的概率为$1/2$ 。当$ \beta $ 随机猜测时，$\overline F $ 不发生的概率是$ 1/({q_H}({q_H} - 1)) $ ，即$ \Pr (F){\kern 1pt} {\kern 1pt} = 1/({q_H}({q_H} - 1)) $ ，${q_H}$ 为$\alpha_2$ 最多询问次数。若
$ \beta $ 不被中止，$ \alpha_2 $ 最多赢得游戏2的概率$1/2$ ，故$ \beta $ 解决$ {\text{DBDH}} $ 困难问题的优势为$$ \begin{split} {\text{Adv}}{\kern 1pt} _\beta ^{{\text{DBDH}}}(k) =& |\Pr {\kern 1pt} {\kern 1pt} [b = b'|F] \cdot \Pr {\kern 1pt} [F]\\ & + |\Pr {\kern 1pt} [b = b'|\overline F ] \cdot \Pr {\kern 1pt} [\overline F ] - 1/2| \\ =& 1/2\Pr {\kern 1pt} [\overline F ] \cdot {{\rm{Adv}}} {\kern 1pt} _{\alpha 2}^\beta (k) \\ =& \frac{1}{{2{q_H}({q_H} - 1)}}{{\rm{Adv}}} {\kern 1pt} _{\alpha 2}^\beta (k)) \end{split} $$ (6) 如果
${\text{Adv}}_{\alpha 2}^\beta (k)$ 是不可忽略的，则${\text{Adv}}_\beta ^{{\text{DBDH}}}(k)$ 不可忽略。因此，该方案具有密文不可区分性。证毕4.3 陷门不可区分性
引理3 若
$ {\text{DBDH}} $ 假设为真，则本文方案满足陷门不可区分性。证明 证明过程与引理2相似，不同之处在于，在引理3的证明中，挑战者
$ \beta $ 随机选择$a \in Z_q^ *$ ，计算$T_1^ * = ag$ ，$T_2^ * = H_2\;(Z'{\kern 1pt} {\kern 1pt} ,\;{w^ * }) + ah$ ，生成挑战陷门$T_w^ * = (T_1^ * ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} T_2^ * )$ 。因篇幅限制，这里省略了详细的证明。4.4 否认性
在本文方案中，接收者在收到密文
$C = (T{\kern 1pt} ,\;C_1{\kern 1pt} {\kern 1pt} {\kern 1pt} , $ $ \;C_2{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\;C_3{\kern 1pt} {\kern 1pt} {\kern 1pt} ,\;V{\kern 1pt} {\kern 1pt} )$ 后，用私钥对密文解密得到明文$ M $ ，运行模拟算法构造$ M $ 的合法密文${C^ * } = ({T^ * },\;C_1^ * ,\;C_2^ *, $ $ \;C_3^ * ,\;{V^ * })$ 。由于密文$C$ 和$ {C^ * } $ 是无法区分的，第三方无法判断$ {C^ * } $ 是发送者或接收者加密后得到，模拟算法如下：(a)计算：
${T^ * } = xQ_{\text{S}}$ ，其中$C_3^ * = xh$ ；(b)计算：
$C_1^* = e{\kern 1pt} {\kern 1pt} {(H_2\;(Z{\kern 1pt} {\kern 1pt} ,\;w)\;,\;{{{\rm{PK}}_{\rm{C}}}})^x}$ ，其中$Z = e{\kern 1pt} {\kern 1pt} ({{{\rm{SK}}_{\rm{S}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ,Q_{\text{R}})$ ；(c)计算：
$C_{\text{2}}^ * = xg$ ，$C_3^ * = xh$ ；(d)计算：
${Y^ * } = H_3\;(w||{{{\rm{ID}}_{\rm{R}}}}||{{\rm{ID}}_{\rm{S}}}\;,\;{T^ * })$ ；(e)计算：
${V^ * } = e{\kern 1pt} {\kern 1pt} (x + {Y^ * }){{{\rm{SK}}_{\rm{S}}}}\;,Q_{\text{R}}\;)$ ；$C{{\kern 1pt} ^ * } = (T{{\kern 1pt} ^ * },\;C_1^ * ,\;C_2^ *,\;C_3^ * ,\;V{{\kern 1pt} ^ * })$ 是接收者运行模拟算法生成的$ M $ 的合法密文，由于密文$ C $ 和$ {C^ * } $ 具有相同的概率分布，第三方无法区分哪个密文由发送者发送，发送者可以否认他已经生成了密文的行为。5. 分析和比较
5.1 安全功能分析
公开发表的文献显示，目前还没有基于身份的具有否认认证的关键字可搜索的加密方案。因此，本文的方案不能与同类方案进行比较。本文方案将在关键字加密、陷门生成和关键字密文检索3个方面与文献[8,10,12]的方案进行比较，表1为各方案功能对比。
从表1可以看出本文方案和文献[8,12]的方案都是在基于身份密码体制下构建且指定测试者，文献[10,12]的方案和本文方案能够抵御内部和外部关键字猜测攻击，文献[8]的方案能够抵御外部关键字猜测攻击，但不能抵御内部关键字猜测攻击。
5.2 计算量分析
表2为各方案计算量对比，
$ {\text{P}} $ 为双线性对运算，$ {\text{E}} $ 为指数运算，$ {\text{M}} $ 为点乘运算，$ {\text{H}} $ 为哈希运算。表3为基本运算所消耗的时间，在关键字加密阶段，本文方案有3个双线性对运算，文献[8,12]分别存在1, 2个双线性对运算，文献[10]没有对运算，计算量由大到小依次为：文献[12]、本文方案、文献[10]、文献[8]；在陷门生成阶段，本文方案与文献[10,12]都存在1个对运算，文献[8]没有对运算，计算量由大到小依次为：文献[12]、文献[10]、本文方案、文献[8]；在关键字密文检索阶段，各个方案都存在2个对运算，文献[8]多出1个哈希运算，文献[12]多出2个指数运算，计算量由大到小依次为：文献[12]、文献[8]、本文方案、文献[10]。综合以上分析，本文方案在关键字加密和生成陷门阶段，计算效率偏低，计算性能上并未占据优势。在关键字密文检索阶段，本文方案与文献[10]的计算效率相似，与文献[8,12]相比，具有更佳的计算性能表现。表 2 计算量对比表 3 不同操作的基本运算耗费时间(ms)TH TE TM TP 时间 3.301 2.864 0.135 3.658 5.3 时间性能分析
本节通过仿真实验将本文方案与文献[8,10,12]的方案在关键字加密、陷门生成和关键字密文检索3个方面进行了对比，加密函数由PBC[18]提供，实验选取关键字Lenovo笔记本(AMD Ryzen 5 4600U with Radeon Graphics @2.10 Hz，16 GB内存和Linux实验选取关键字分别为：1, 50, 100, 300, 500, 700, 900, 1000，实验结果如图2所示。从图2可以看出在关键字加密阶段，随着关键字数量的增加，关键字加密的时间也在增加，在关键字数量相同的情况下，本文方案在加密阶段加密时间小于文献 [12]，本文方案比文献[8]多出2个对运算，加密时间比文献[8]要长。在陷门生成阶段，本文方案与文献[10,12]均有1个对运算，但文献[12]存在2个指数运算，文献[10]存在1个指数运算，本文方案相较于文献[10,12]，优势在于在该阶段没有指数运算，生成陷门的时间相对较短，文献[8]在该阶段不存在对运算和指数运算，生成陷门时间比本文方案要短。在关键字密文检索阶段，各方案均有2个对运算，文献[12]多出了2个指数运算，运算时间相对于其他方案较长，本文方案在关键字密文检索阶段比文献[8,10]多出了2个点乘运算时间，文献[8]比本文方案和文献[10]多出1个哈希运算。由表3可以看出，点乘耗费时间最短，检索关键字密文所耗费的时间本文方案接近于文献[10]。本文方案在各个阶段的计算所消耗的时间相较于其他3种方案有长有短，但本文最大的优势在于实现了否认属性，对发送者的隐私有了很好的保护，在电子邮件、医疗信息等方面有着较好的应用前景。
6. 结束语
本文方案将关键字可搜索加密与否认认证加密相结合，基于BDH和DBDH困难问题证明了方案满足不可伪造性、密文和陷门的不可区分性。本文方案中的否认属性，在保护发送者身份隐私上具有较高的实用性。不足的是本文方案基于身份密码体制构建，基于身份的密码体制虽解决了PKI中的证书管理问题，但也存在密钥托管和密钥撤销的缺陷，未来我们将否认认证加密迁移到无证书密码体制下，利用无证书优势解决密钥托管问题。
-
[1] 白利芳, 祝跃飞, 芦斌. 云数据存储安全审计研究及进展[J]. 计算机科学, 2020, 47(10): 290–300. doi: 10.11896/jsjkx.191000111BAI Lifang, ZHU Yuefei, and LU Bin. Research and development of data storage security audit in cloud[J]. Computer Science, 2020, 47(10): 290–300. doi: 10.11896/jsjkx.191000111 [2] 韩培义, 刘川意, 王佳慧, 等. 面向云存储的数据加密系统与技术研究[J]. 通信学报, 2020, 41(8): 55–65. doi: 10.11959/j.issn.1000-436x.2020140HAN Peiyi, LIU Chuanyi, WANG Jiahui, et al. Research on data encryption system and technology for cloud storage[J]. Journal on Communications, 2020, 41(8): 55–65. doi: 10.11959/j.issn.1000-436x.2020140 [3] YANG Ningbin, XU Shumei, and QUAN Zhou. An efficient public key searchable encryption scheme for mobile smart terminal[J]. IEEE Access, 2020, 8: 77940–77950. doi: 10.1109/ACCESS.2020.2989628 [4] BONEH D, DI CRESCENZO G, OSTROVSKY R, et al. Public key encryption with keyword search[C]. International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2004: 506–522. doi: 10.1007/978-3-540-24676-3_30. [5] BYUN J W, RHEE H S, PARK H A, et al. Off-line keyword guessing attacks on recent keyword search schemes over encrypted data[C]. The 3rd VLDB Workshop on Secure Data Management, Seoul, South Korea, 2006: 75–83. doi: 10.1007/11844662_6. [6] LU Yang and LI Jiguo. Efficient searchable public key encryption against keyword guessing attacks for cloud-based EMR systems[J]. Cluster Computing, 2019, 22(1): 285–299. doi: 10.1007/s10586-018-2855-y [7] LIN Qun, YAN Hongyang, HUANG Zhengan, et al. An ID-based linearly homomorphic signature scheme and its application in blockchain[J]. IEEE Access, 2018, 6: 20632–20640. doi: 10.1109/ACCESS.2018.2809426 [8] WU T Y, TSAI T T, and TSENG Y M. Efficient searchable ID-based encryption with a designated server[J]. Annals of Telecommunications-Annales Des Télécommunications, 2014, 69(7/8): 391–402. doi: 10.1007/s12243-013-0398-z [9] 王少辉, 韩志杰, 肖甫, 等. 指定测试者的基于身份可搜索加密方案[J]. 通信学报, 2014, 35(7): 22–32. doi: 10.3969/j.issn.1000-436x.2014.07.003WANG Shaohui, HAN Zhijie, XIAO Fu, et al. Identity-based searchable encryption scheme with a designated tester[J]. Journal on Communications, 2014, 35(7): 22–32. doi: 10.3969/j.issn.1000-436x.2014.07.003 [10] HUANG Qiong and LI Hongbo. An efficient public-key searchable encryption scheme secure against inside keyword guessing attacks[J]. Information Sciences, 2017, 403/404: 1–14. doi: 10.1016/j.ins.2017.03.038 [11] BAEK J, SAFAVI-NAINI R, and SUSILO W. Public key encryption with keyword search revisited[C]. 2008 International Conference on Computational Science and its Applications, Perugia, Italy, 2008: 1249–1259. doi: 10.1007/978-3-540-69839-5_96. [12] LI Hongbo, HUANG Qiong, SHEN Jian, et al. Designated-server identity-based authenticated encryption with keyword search for encrypted emails[J]. Information Sciences, 2019, 481: 330–343. doi: 10.1016/j.ins.2019.01.004 [13] LU Yang and LI Jiguo. Constructing designated server public key encryption with keyword search schemes withstanding keyword guessing attacks[J]. International Journal of Communication Systems, 2019, 32(3): e3862. doi: 10.1002/dac.3862 [14] DWORK C, NAOR M, and SAHAI A. Concurrent Zero-knowledge[J]. Journal of the ACM, 2004, 51(6): 851–898. doi: 10.1145/1039488.1039489 [15] LI Fagen, ZHENG Zhaohui, and JIN Chunhua. Identity-based deniable authenticated encryption and its application to e-mail system[J]. Telecommunication Systems, 2016, 62(4): 625–639. doi: 10.1007/s11235-015-0099-1 [16] WU Weifeng and LI Fagen. An efficient identity-based deniable authenticated encryption scheme[J]. KSII Transactions on Internet and Information Systems, 2015, 9(5): 1904–1919. doi: 10.3837/tiis.2015.05.020 [17] POINTCHEVAL D and STERN J. Security arguments for digital signatures and blind signatures[J]. Journal of Cryptology, 2000, 13(3): 361–396. doi: 10.1007/s001450010003 [18] PBC Library. The pairing-based cryptography library[EB/OL]. http://crypto.stanford.edu/pbc/, 2015. 期刊类型引用(7)
1. 孟贤，刘吉成. 基于区块链技术的电力供应链资源安全共享. 计算机仿真. 2024(10): 69-73 . 
百度学术2. 陈怡馨，马曾. 无线网络信息差分隐私的动态可搜索加密仿真. 计算机仿真. 2024(10): 424-427+442 . 百度学术3. 郑东，康春蕾，郭瑞. 基于智能合约的多用户匿名无证书可搜索加密方案. 西安邮电大学学报. 2024(06): 34-41 . 百度学术4. 郭瑞，李晨烨，朱天泽. 基于区块链与可搜索加密的电子病历共享方案. 西安邮电大学学报. 2024(06): 65-72 . 百度学术5. 宋安宁，王宝成，李化鹏. 基于无证书的具有否认认证的可搜索加密方案. 计算机应用研究. 2023(05): 1510-1514 . 百度学术6. 郑东，何俊杰，秦宝东，陈从正. 可撤销的多关键字公钥可搜索加密方案. 计算机应用研究. 2023(07): 2179-2183+2191 . 百度学术7. 姜春峰. 基于属性分类的分布式大数据隐私保护加密控制模型设计. 计算机测量与控制. 2023(11): 221-227 . 百度学术其他类型引用(8)
-
下载:
下载:
百度学术
计量
- 文章访问数: 1188
- HTML全文浏览量: 598
- PDF下载量: 185
- 被引次数: 15
下载:
