Firing Characteristics Analysis of the Fractional-order Extended Hindmarsh-Rose Neuronal Model under Transcranial Magneto-Acoustical Stimulation
-
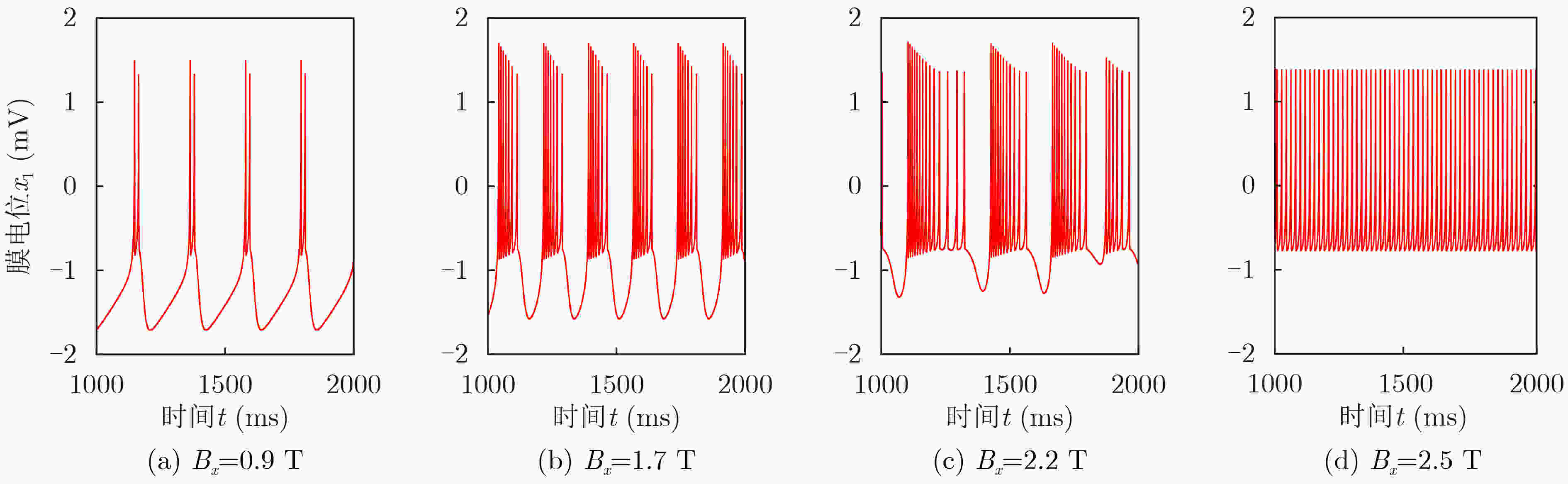
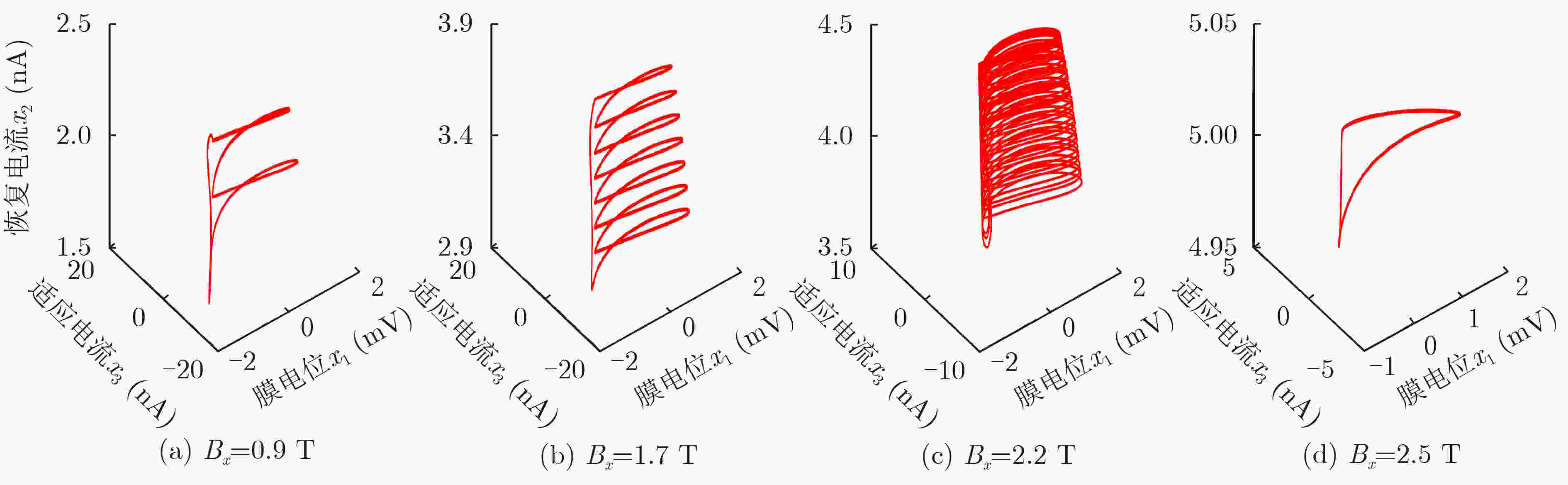
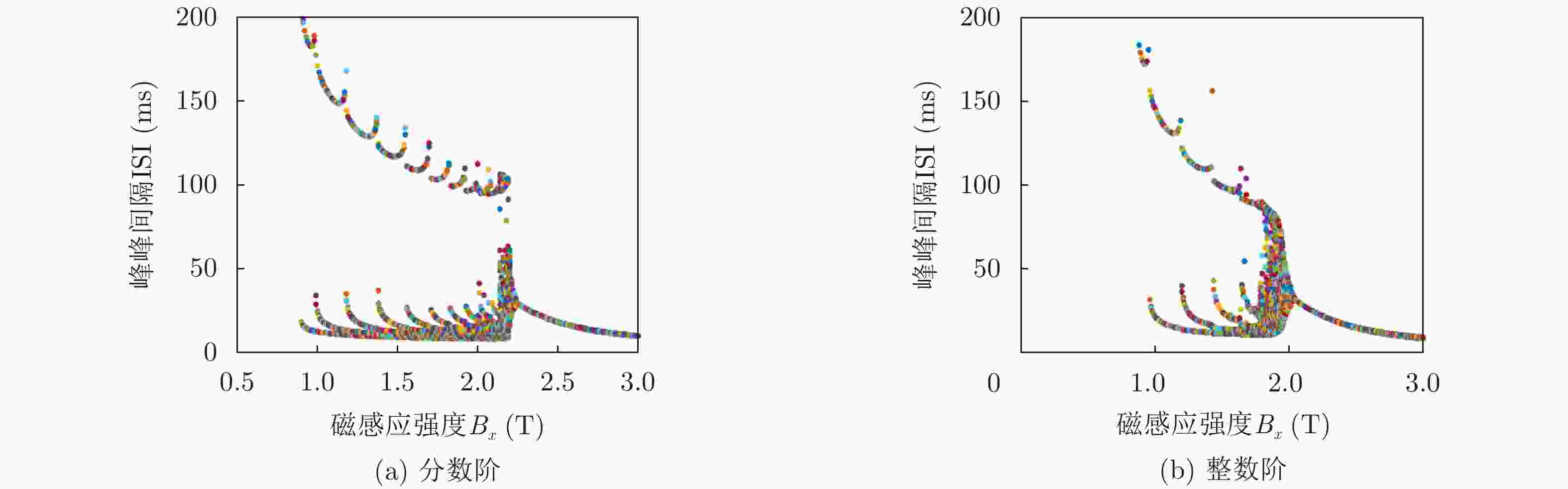
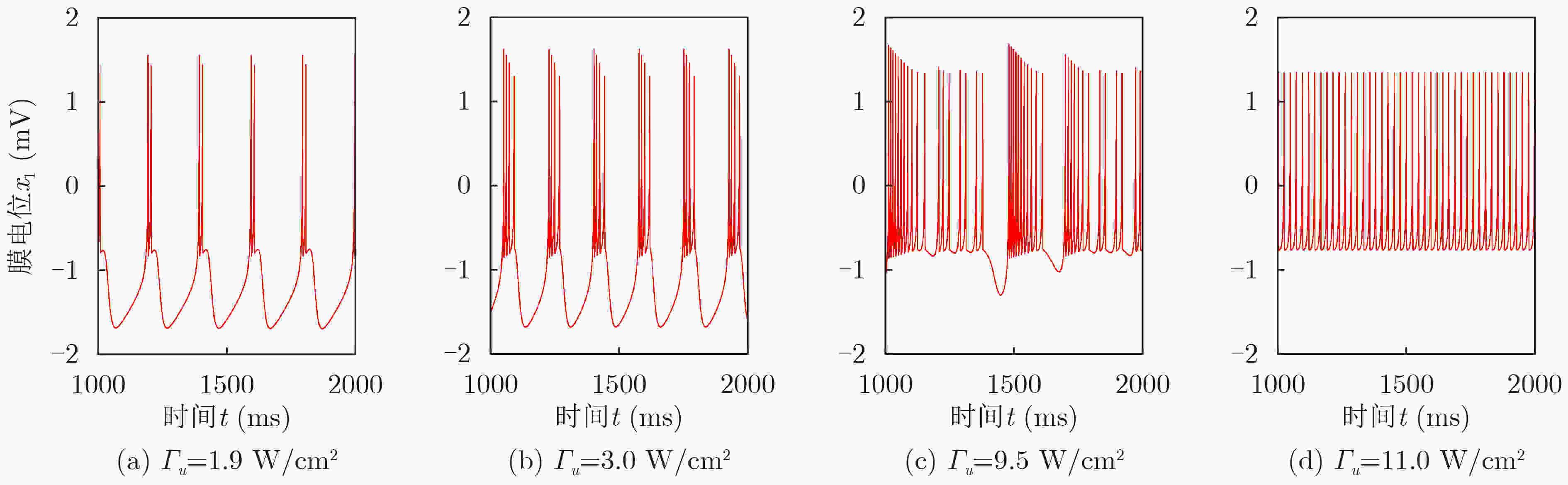
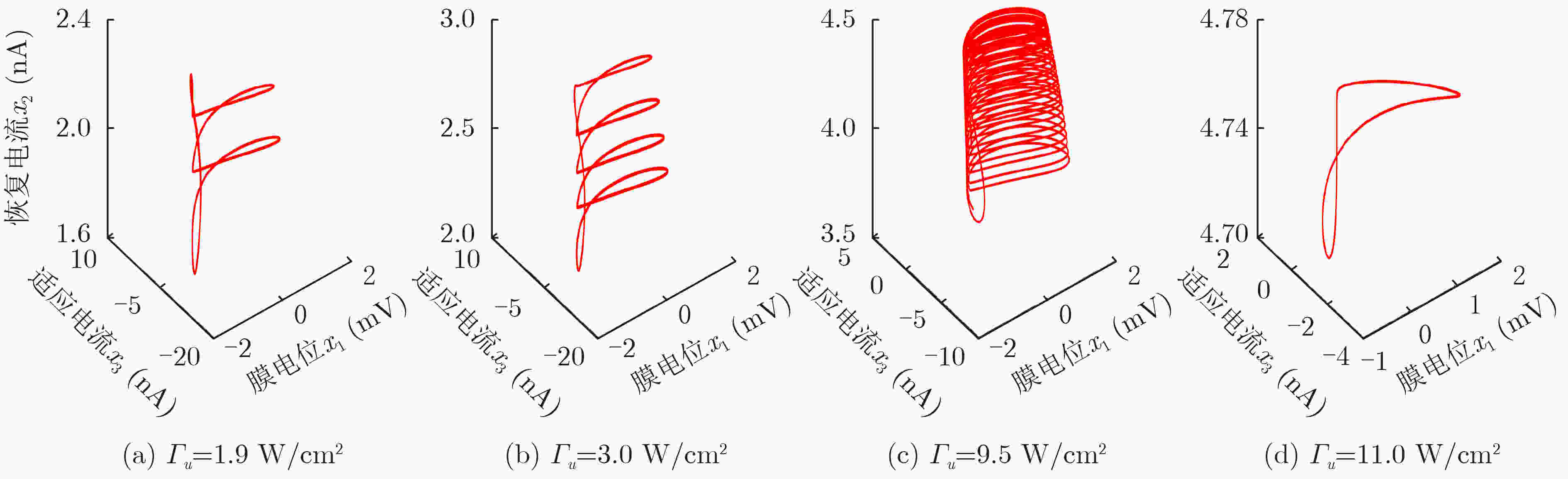
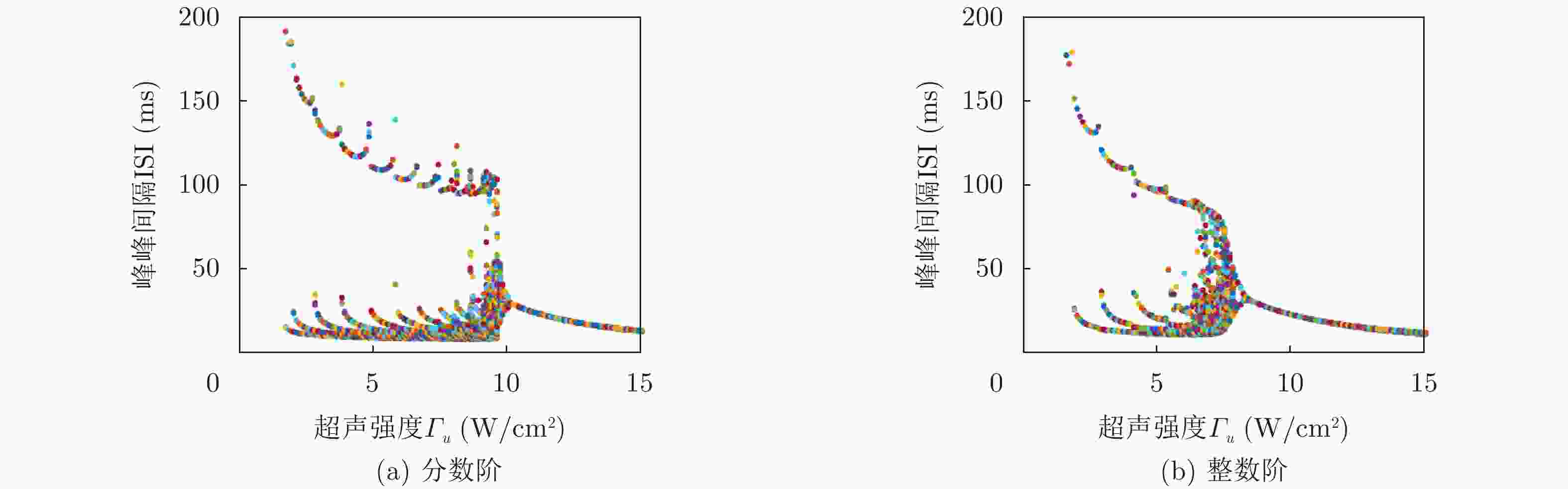
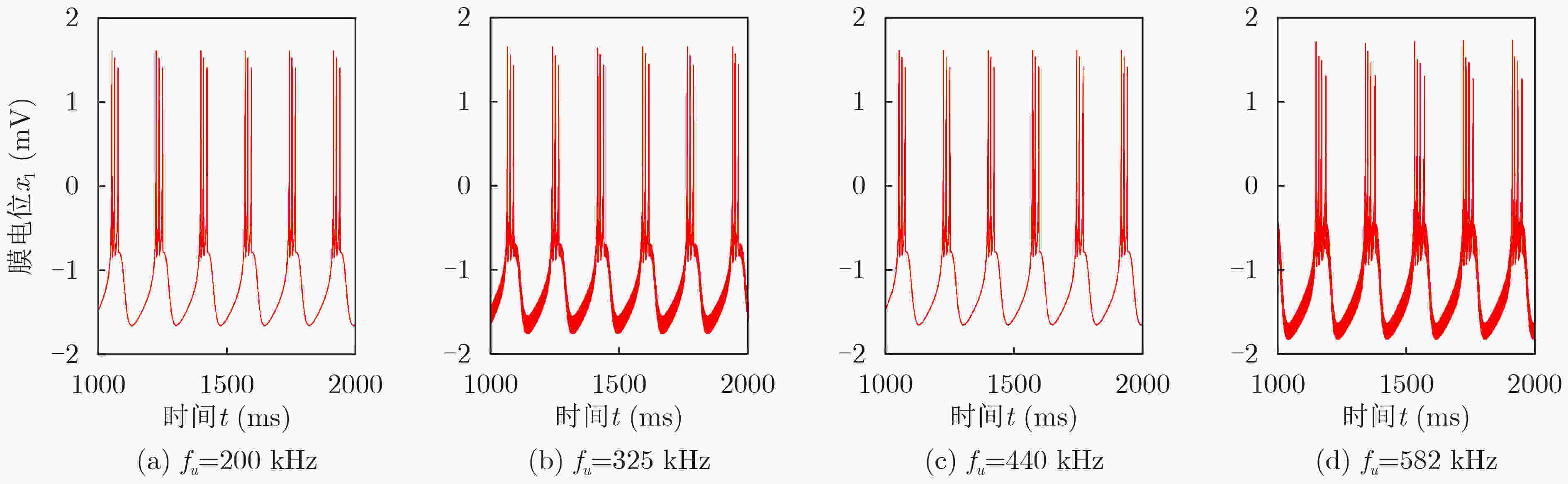
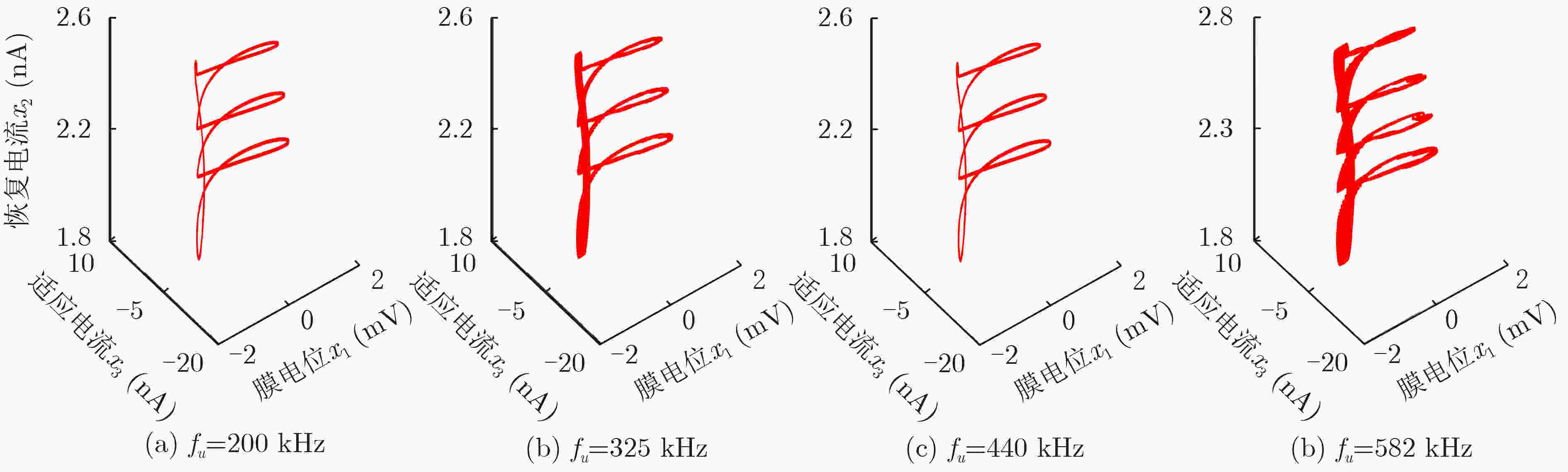
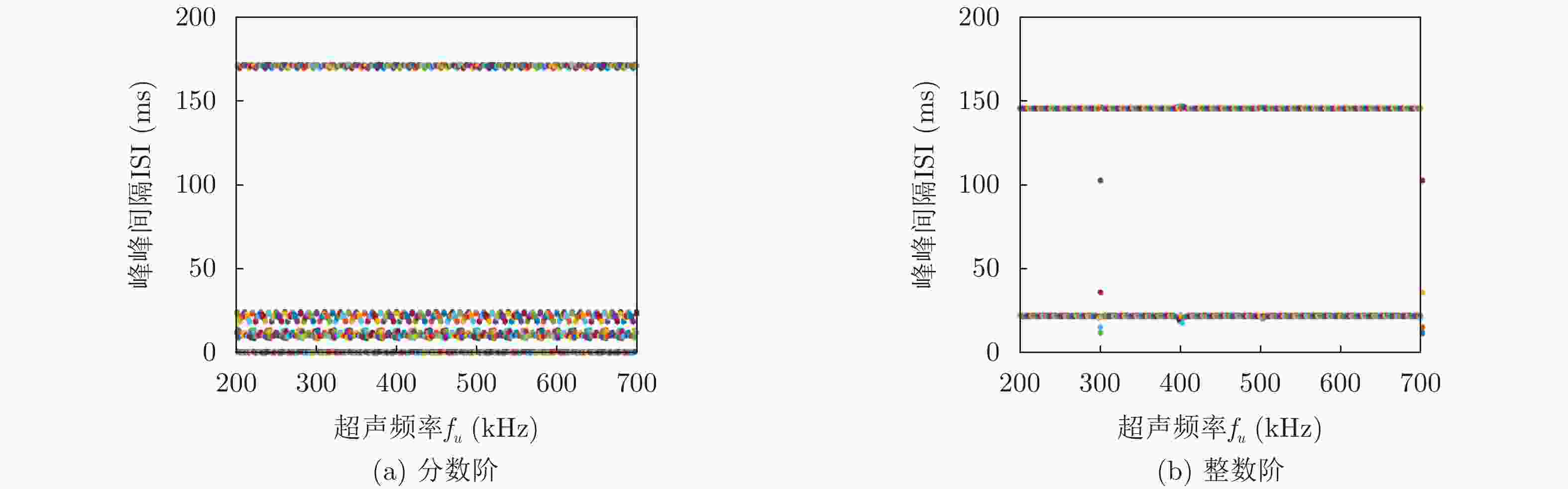
摘要: 该文基于分数阶扩展Hindmarsh-Rose(HR)神经元模型，对其在经颅磁声刺激(TMAS)影响下的放电模式和放电频率进行了分析研究。作为神经元的外部刺激输入，具有不同磁声参数的经颅磁声刺激产生的交变电流会对神经元的放电特性产生不同的影响。通过对不同磁感应强度、超声强度以及超声频率下神经元的膜电位曲线以及以磁声参数为变量的峰峰间隔分岔图进行定量分析可知，分数阶扩展HR神经元模型放电模式和放电节律的调节可通过改变经颅磁声刺激的磁感应强度和超声强度来实现。然而，超声频率的改变不会对神经元放电模式产生影响，但其取值变化会在小范围内影响神经元的放电频率。此外，通过对比分数阶与整数阶神经元在不同磁声参数交变电流刺激下的放电特性可知，分数阶扩展HR神经元模型具有更多变的放电模式和更复杂的放电节律。该文的结论有利于了解经颅磁声刺激的影响机制，进而为其实验和临床应用提供理论依据。
-
关键词:
- 经颅磁声刺激 /
- 放电特性 /
- 分数阶 /
- Hindmarsh-Rose神经元模型 /
- 混沌
Abstract: In this paper, the firing modes and spike frequencies of the fractional-order extended Hindmarsh-Rose(HR) neuronal model under Transcranial Magneto-Acoustical Stimulation (TMAS) are investigated. The TMAS with different parameters generate different alternating current and further have various effect on the firing characteristics of the neuronal model. To address the effect of TMAS on firing characteristics under different ultrasound and magnetic field parameters, the membrane potential curves and bifurcation diagrams are exhibited and analyzed. The results show that the firing mode and spike frequency are strongly dependent on the ultrasonic and magnetic field intensities. It is also found that there is no influence of the ultrasonic frequency on the firing mode, though it changes the firing frequency over a small range. Moreover, compared with the integer-order neuronal model, the fractional-order extended HR neuronal model exhibits more variable firing modes and more complex discharge rhythms. These conclusions reveal the influencing mechanism of TMAS and can be taken as theoretical basis for TMAS experimental and clinical application. -
1. 引言
神经元是神经系统的重要组成部分，是神经系统进行信息传递和处理的核心。神经元的放电特性与神经系统模式识别及脑信号测量息息相关。神经元的放电特性具有混沌特性，其放电模式会随着外部输入电流等分岔参数的变化而表现为静止、脉冲放电、簇放电和混沌放电等完全不同的形式。为此，很多无创的外部刺激技术被应用于神经系统疾病的治疗当中，例如，经颅电刺激、经颅磁刺激、经颅超声刺激以及经颅磁声刺激等[1-3]。
经颅磁声刺激是一种利用静态磁场和超声波在脑组织液中产生刺激电流的无创脑刺激技术。经颅磁声刺激不仅在空间分辨率和穿透深度方面具有明显优势，而且可通过提高局部场电位的幅值，进而增强集中超声刺激对神经调节的作用[4]。实验表明，经颅磁声刺激可以改变神经元的放电节律和Ca2+离子浓度[5]。因此，经颅磁声刺激成为癫痫、帕金森等神经系统疾病的潜在治疗手段，并在近几年得到了快速发展。经颅磁声刺激由磁场和超声共同作用，其作用电流受磁感应强度、超声强度、超声频率多个磁声参数影响，具有复杂的放电特性[6]。
迄今为止，研究者已经提出了多种神经元模型，用以描述神经元的生物特性及其放电节律。最经典的神经元模型为Hodgkin-Huxley(HH)模型，该模型由4个非线性微分方程组成，描述了巨大轴突乌贼神经元系统中的离子活动[7]。其他常用的神经元模型有Hindmarsh-Rose(HR)模型[8]、FitzHugh-Nagumo(FHN)模型[9]、Ermentrout模型[10]、Morris-Lecar模型[11]和积分-发射模型[12]等。在现有神经元模型中，基于电导的HH神经元模型具有较高的生物学精度，是目前最真实的神经系统模型之一，但其结构复杂，需要较高的计算成本。因此，针对神经元模型系统的数学分析，需要在生物精度和计算代价之间进行权衡。为此，随后的研究者根据其他生物神经元的电活动，提出了一系列维数较低的简化模型，如主要用于描述心电学上的电活动的FHN模型和本文使用的主要用于模拟大脑丘体神经元的放电行为的HR模型。基于脉冲形态的HR模型常应用于大脑神经元模型的动态特性分析与同步控制研究。
随着神经元模型研究的深入，很多改进的HR神经元模型被提出，针对改进神经元模型动力学行为的研究就此展开。Moujahid等人[13]考虑到神经系统中复杂的电磁场分布，在经典HR神经元模型中引入一个表示磁通量的变量，从而建立了一个4变量的HR神经元模型。基于此模型，Lü等人[14]不仅研究了神经元细胞内外电磁感应对神经元放电节律的影响，还考虑了外部电磁辐射对神经元放电模式的影响。研究发现，考虑电磁辐射的HR神经元模型具有更丰富的分岔参数，其表现的复杂放电特性符合神经元的生物特性。为进一步提高HR神经元模型的生物学特性，文献[15]提出了一个扩展的HR神经元模型，该模型也由4个变量组成，引入的变量表示细胞内钙离子在细胞质与其存储区之间的交换。通过动态特性分析与实验验证发现，该扩展HR神经元模型的动态特性与神经元的生物学特性一致，相比于经典HR神经元模型，更符合真实神经元的电活动特征，更适用于神经元的放电特性分析[16,17]。针对此扩展HR神经元模型，文献[18]通过计算平衡点、李雅普诺夫指数以及绘制分岔图讨论了直流电刺激下扩展HR神经元模型的动态特性，并研究了直流外部输入对神经元放电特性的影响。然而，现有文献对其进行的动态特性研究均基于直流电刺激，而经颅磁声刺激是通过无创经颅刺激技术产生交变电流作为神经元的外部刺激输入，刺激电流的变化会使神经元表现出完全不同的更复杂的放电特性。
此外，经典神经元模型由整数阶微分方程表示。然而，随着神经科学的发展，研究人员在实验中发现分数阶微分更符合大鼠新皮层锥体神经元多时间尺度适应的放电特性[19]。Anastasio[20]发现脑干前庭动眼神经细胞的电生理特征更符合分数阶动力学特性。而且，分数阶微分方程可以看作理想整数阶微分方程的一般形式，能更准确地描述某些物理现象。因此，分数阶神经元模型在描述神经动力学行为方面比整数阶模型更有优势。文献[21,22]以具有直流电输入的分数阶经典HR神经元模型为研究对象，分别将直流外部输入和分数阶次作为分岔参数，通过定量分析研究了分数阶HR神经元模型的分岔特性。研究发现，相比整数阶模型，分数阶HR神经元模型具有更复杂的动态特性，具有不同直流外部输入或分数阶次的神经元模型，均可能表现出完全不同的放电模式或放电节律。针对改进的分数阶扩展HR神经元模型，文献[23]通过平衡点计算和李雅普诺夫指数讨论了此改进HR神经元模型的动态特性，并设计控制算法实现了两个耦合神经元的同步控制。然而，现有文献对此改进HR神经元模型的动态特性研究均基于直流电刺激。在神经系统疾病的治疗中，许多非侵入性脑刺激疗法，如经颅磁声刺激、经颅磁刺激等，均是通过产生交变电流作为神经元的外部输入以改变其放电特性。因此，本文以更符合神经元生物特性的分数阶扩展HR神经元模型为研究对象，考虑经颅磁声刺激交变电流的影响，分析其在不同磁声参数作用下的放电模式和放电频率，并将其放电特性与相同参数下的整数阶神经元模型对比，对经颅磁声刺激输入下分数阶扩展HR神经元的放电特性展开研究。
2. 问题描述
2.1 经颅磁声刺激
经颅磁声刺激利用静磁场和超声波的双重作用形成刺激电流，其原理为神经元在经颅磁声刺激的作用下，其组织液中的带电离子随着超声波的传播而发生移动，同时受外加静磁场的影响，带正负电荷离子受到洛伦兹力的作用而向相反方向移动，形成脑刺激电流。因此，经颅磁声刺激对神经元的影响可用神经元系统中与超声波、静磁场和组织液特性有关的调制正弦交流电流来描述，其表达式为
Iext=σBx√2Γuρc0sin((2πfut)+1) (1) 其中，σ 为神经元组织液的电导率，ρ为组织液的密度，c0为超声波传播速度，其典型值分别为σ = 0.5 Siemens/m, ρ =1120 kg/m3 以及c0 =1540 m/s。此外，Bx为静磁感应强度，Γu为超声场强度，fu为超声频率[24-27]。在仿真分析中，将以这些磁声参数作为经颅磁声刺激的可调变量，分析其对神经元动态特性的影响。本文考虑的磁声参数取值范围如表1所示。
表 1 磁声参数的可调范围磁声参数变量 可调范围 Bx 0.5～3.0 T Γu 0.5～15 W/cm2 fu 100～600 kHz 2.2 分数阶扩展HR神经元模型
经典的三变量HR神经元模型因其在计算速度方面的优势被广泛地应用于神经元动态性能的研究。其模型可描述为
˙x1=x2−ax31−bx21−x3+Iext˙x2=c−dx21−x2˙x3=r(S(x1−x0)−x3)} (2) 其中，x1为膜电位，x2为恢复性快电流，x3为适应性慢电流。Iext表示作用于神经元的外部刺激输入电荷。a, b, c, d, r, S和x0均为模型参数，其中，x0表示Iext =0时的静息膜电位，r表示慢离子通道的变化速率且 0<r
≪ 1[28]。随着神经科学的发展，典型的三变量HR模型在描述神经元复杂的非线性和精确的行为模式方面存在局限性。因此，科研人员提出了一种改进的扩展HR神经模型，该模型引入了一个新的变量x4来描述细胞内钙离子在细胞质和其存储介质之间的缓慢交换。扩展HR神经元整数阶模型可由式(3)微分方程表示
˙x1=x2−ax31−bx21−x3+Iext˙x2=c−dx21−x2−ex4˙x3=r(S(x1−x0)−x3)˙x4=h(−px4+f(x2+g))} (3) 其中，h, p, f和g为变量x4新引入的模型参数[13,21]。
随着神经科学的发展，分数阶神经元模型被发现相比于整数阶神经元模型更具普遍性和准确性。为此，下面介绍分数阶定义，将扩展HR神经元改进为分数阶形式，并对其在经颅磁声刺激作用下的放电模式进行研究。分数阶导数的微分方程具有多种形式，其中，Caputo定义相比其他定义具有更明确的物理意义。
定义1[29] 函数x(t)的Caputo分数阶微分定义为
c0Dqtx(t)=1Γ(n−q)∫t0(t−τ)−q+n−1x(n)(τ)dτ (4) 其中，t ≥ 0, q为分数阶次，n为满足n–1<q<n的最小整数。
Γ (⋅)为Gamma函数。为简化表达，本文用
Dqtx(t) 代替c0Dqtx(t) 表示Caputo分数阶微分。由此，分数阶扩展HR神经元模型可表示为Dqtx1=x2−ax31−bx21−x3+IextDqtx2=c−dx21−x2−ex4Dqtx3=r(S(x1−x0)−x3)Dqtx4=h(−px4+f(x2+g))} (5) 在相关文献中，对HR神经元模型放电节律的研究主要以直流刺激作为外部输入。但大多数无创的经颅脑刺激方法，如经颅磁刺激、经颅超声刺激和经颅磁声刺激均通过产生交变电流改变神经元的放电节律。因此，本文以经颅磁声刺激作用下的分数阶扩展HR神经元模型为研究对象。其系统模型可由式(5)表示，式中经颅磁声刺激产生的外部输入电流Iext可写为式(1)形式，其值随磁感应强度、超声场强度和超声频率的变化而变化。本文的仿真实验选定如下扩展HR神经元模型参数：a=1, b=3, c=1, d=5, e=0.125, f=0.88, g=0.9, r=0.006, S=4, p=1, h=0.0002, x0=–1.56，且模型状态变量初始值为[x1(0), x2(0), x3(0), x4(0)]=[0.1, 0.3, 3, –0.3]。
3. 神经元系统放电特性分析
为了研究经颅磁声刺激作用下的分数阶扩展HR神经元的放电特性，本文分别以磁感应强度、超声强度和超声频率为变量，应用Matlab软件进行仿真并对生成的膜电位曲线、
x1x2x3 相图和峰峰间距分岔图进行定量分析。3.1 磁感应强度对神经元放电特性的影响
为了研究磁感应强度对神经元放电特性的影响，选定磁感应强度Bx为变量，其变化区间为0.5 T≤Bx≤3.0 T。超声强度和超声频率选取固定值Γu=0.5 W/cm2和fu=350 kHz。选取分数阶次q=0.98，其放电特性如图1—图3所示。
图1(a)—图1(d)分别为磁感应强度Bx为0.9 T, 1.7 T, 2.2 T和2.5 T时分数阶扩展HR神经元的膜电位曲线，图2(a)—图2(d)为与之相对应的不同磁感应强度下的神经元模型
x1x2x3 相图。如图1、图2所示，随着磁感应强度的变化，神经元呈现多种不同的放电模式。当Bx=0.9 T时，神经元表现为双周期的簇放电形式，且簇间间距较大，簇内峰峰间距较小(如图1(a)和图2(a)所示)。当Bx=1.7 T时，神经元表现为6周期簇放电形式，且簇内峰峰间距逐渐增大(如图1(b)和图2(b)所示)。而且，对比Bx=0.9 T与Bx=1.7 T时的神经元放电节律可见，随着磁感应强度的增大，其簇间间距减小，放电频率增大。当Bx=2.2 T时，神经元表现出混沌放电形式(如图1(c)和图2(c)所示)。当Bx=2.5 T时，神经元呈现高频率单周期脉冲放电模式(如图1(d)和图2(d)所示)。除此之外，由图1、图2可见，随着磁感应强度的增大，神经元的放电频率整体呈增大趋势，神经元膜电位最大值基本不变，但其最小值逐渐增大，因此，神经元膜电位的幅值呈逐渐减小趋势。为进一步观察不同磁感应强度下分数阶扩展HR神经元的放电特性，本文针对以磁感应强度为分岔参数的膜电位峰峰间距分叉图(如图3(a)所示)进行定量分析。在磁感应强度变化范围内，当0.5 T≤Bx<0.86 T时，神经元处于静止状态。当Bx≥0.86 T时，神经元进入双周期簇放电形式，且随着磁感应强度增大，峰峰间隔逐渐减小，簇间间隔呈先减小后增大趋势。之后当磁感应强度处于0.98 T≤Bx<1.74 T范围内时，神经元依然表现为簇放电形式，但其节律从3周期逐渐增加至6周期，且在每种周期簇放电模式下，簇间间距均表现为随着磁感应强度的增大先减小再增大。与此同时，神经元放电周期的递增是随着原有周期模式内簇内脉冲频率趋于一致时产生一个新的脉冲而变化的。当1.74 T≤Bx<2.18 T时，神经元依然表现为周期逐个递增的簇放电模式。但与之前阶段不同的是，其簇间间距随着磁感应强度的增大而增大。当2.18 T≤Bx<2.24 T时，神经元处于混沌放电模式。当Bx=2.24 T，神经元表现为双周期簇放电，之后当Bx≥2.25 T，神经元进入单周期脉冲放电状态，且放电频率随磁感应强度的增加而增大。
此外，为对比磁感应强度变化对分数阶与整数阶扩展HR神经元的影响，以磁感应强度为变量的整数阶神经元膜电位峰峰间距分叉图如图3(b)所示。可知，分数阶与整数阶神经元模型的放电模式与放电节律变化趋势基本一致。但随着磁感应强度的增大，分数阶神经元比整数阶神经元更快进入簇放电模式，且在以磁感应强度为变量的经颅磁声刺激作用下的分数阶神经元模型具有更复杂的放电特性，其具体表现为更多变的放电模式和更复杂的分岔特性。
3.2 超声强度对神经元放电特性的影响
选定超声强度变化范围为0.5 W/cm2≤ Γu ≤15 W/cm2，超声频率fu=350 kHz，磁感应强度Bx=0.5 T，扩展HR神经元放电特性如图4、图5所示。
图4(a)—图4(d)和图5(a)—图5(d)分别为超声强度Γu为1.9 W/cm2, 3.0 W/cm2, 9.5 W/cm2和11.0 W/cm2时的神经元膜电位曲线及其
x1x2x3 相图。可以看出，不同超声强度下的分数阶扩展HR神经元具有不同的放电模式。当Γu=1.9 W/cm2时，神经元呈现双周期的簇放电模式，且簇内峰频率较簇间放电频率较大(如图4(a)和图5(a)所示)。当超声场强度增大至Γu=3.0 W/cm2时，可观察神经元依然呈簇放电形式，但其放电节律变化为4周期，且簇间放电频率增大，簇内峰峰间隔呈增大趋势(如图4(b)和图5(b)所示)。当Γu=9.5 W/cm2时，神经元呈现混沌放电模式(如图4(c)和图5(c)所示)。而当Γu=11.0 W/cm2时，神经元进入频率较高的单周期脉冲放电模式。对比图4(d)和图5(d)可知，随着超声强度增加，神经元膜电位最小值逐渐增大，膜电位曲线幅值逐渐减小，神经元放电频率整体呈增大趋势。通过绘制以超声场强度为分岔参数的膜电位峰峰间距分叉图(如图6)，可观察到不同超声场强度下神经元模型的放电节律，对其进行定量分析可知超声场强度对分数阶扩展HR神经元放电特性的影响。不同超声场强度下分数阶扩展HR神经元膜电位峰峰间距分叉图如图6(a)所示，对其进行定量分析可知，当Γu≤1.5 W/cm2时，神经元呈现静止状态，直至进入双周期簇放电模式。当1.5 W/cm2<Γu ≤8.9 W/cm2时，随着超声场强度的增加，神经元表现为周期个数逐渐递增的簇放电形式，且其放电脉冲的增加均以原有放电模式中簇内峰峰间距向较小值趋于一致为前提。因此，在同一种周期性簇放电模式中，神经元膜电位曲线的簇内峰峰间距呈逐渐减小趋势。值得注意的是，随着超声强度的变化，神经元膜电位的簇间频率的变化趋势有所不同。当1.5 W/cm2<Γu ≤6.0 W/cm2时，神经元膜电位簇间间距表现为先减小后增大，而当6.1 W/cm2<Γu ≤8.9 W/cm2时，神经元膜电位簇间间距呈增大趋势。当8.9 W/cm2<Γu ≤9.9 W/cm2时，神经元进入混沌放电状态，直至Γu≥9.9 W/cm2，神经元恢复至双周期簇放电模式。当超声场强度继续增大至Γu>10.1 W/cm2时，神经元进入单周期脉冲放电模式，且随着超声场强度的增大，其放电频率逐渐升高。
将不同超声场强度下的分数阶(q=0.98)扩展HR神经元峰峰间距分叉图与其整数阶(q=1)分叉图对比可得，不同超声场强度经颅磁声刺激下的分数阶神经元与整数阶神经元的放电特性变化趋势大致相同，但在相同的超声强度变化范围内，分数阶神经元呈现出更多种的放电模式和更多变的放电节律。
3.3 超声频率对神经元放电特性的影响
针对经颅磁声刺激参数，选取磁感应强度及超声场强度分别为Bx=0.8 T和Γu =1.0 W/cm2，分数阶次q=0.98，当超声频率变化范围为200 kHz≤fu≤700 kHz时，分数阶扩展HR神经元的放电特性如图7、图8所示。
当超声频率fu分别为200 kHz, 325 kHz, 440 kHz和582 kHz时，分数阶扩展HR神经元膜电位曲线及
x1x2x3 相图如图7、图8所示。当磁感应强度和超声场强度为选取的固定值，超声频率fu=200 kHz时，神经元表现为3周期簇放电形式(如图7(a)和图8(a)所示)。当超声频率增大至fu=325 kHz时，神经元依然呈现3周期簇放电形式，且其膜电位幅值、簇间间距和簇内峰峰间距均变化不大。但是当膜电势处于负电位值时，其值出现了小幅度高频率波动(如图7(b)和图8(b)所示)。当超声频率fu=440 kHz，神经元放电模式和放电频率与fu=200 kHz时完全相同(如图7(c)和图8(c)所示）。而当超声频率继续增大到fu=582 kHz时，神经元发生放电模式的改变，由3周期簇放电变化为4周期簇放电形式，但其电位幅值和簇间频率不变。然而，与fu=325 kHz时放电特性相似，当fu=582 kHz时，神经元膜电势同样表现出低电位值高频率波动现象(如图7(d)和图8(d)所示)。为进一步分析超声频率对分数阶(q=0.98)扩展HR神经元放电特性的影响，本文对如图9(a)所示的神经元膜电位峰峰间距曲线进行分析。当超声频率为200 kHz ≤fu≤700 kHz时，神经元均处于簇放电模式，且其簇间频率基本不变。当超声频率为10 kHz的整数倍时，分数阶扩展HR神经元均呈现相同的放电特性。然而，当超声频率为取值范围内的其他值时，神经元膜电位簇内脉冲个数和脉冲频率均出现小幅度波动。
由整数阶(q=1)扩展HR神经元膜电位峰峰间距分岔图(如图9(b)所示)可知，当超声频率处于200 kHz ≤fu≤700 kHz时，神经元在大多数超声频率取值下的放电模式和放电节律相同。然而，当超声频率为100 kHz的整数倍时，神经元的放电节律会呈现与其他取值不同的形式。例如，当fu为300 kHz和700 kHz时，神经元呈现6周期放电形式，而当fu为400 kHz和500 kHz时，神经元放电模式不变，但其放电频率发生小幅度改变。而对比分数阶扩展HR神经元膜电位峰峰间距分岔图可得，超声频率对分数阶神经元模型放电特性的影响更明显，不同超声频率下的分数阶神经元具有更复杂的放电特性。
4. 结束语
本文以经颅磁声刺激参数为变量，讨论了不同磁感应强度、超声强度和超声频率对分数阶扩展HR神经元放电特性的影响。通过对基于Matlab的仿真结果进行的定量分析可知，当磁感应强度和超声场强度都较小时，神经元处于静止状态，即无放电行为。随着磁感应强度或超声场强度的增大，由式(1)可知，经颅磁声刺激产生的交变电流幅值增大，神经元先后呈现多周期簇放电、混沌放电和高频率单周期脉冲放电形式，且伴随神经元膜电位幅值逐渐减小，脉冲放电频率逐渐增高。当神经元处于簇放电模式时，随着刺激交变电流幅值的增大，其簇内脉冲个数逐渐增多，且簇内脉冲频率向较小值趋于一致。当然，在相同周期的簇放电模式内，当刺激电流幅值在较低值范围内增大时，其簇间频率逐渐增高，而当刺激电流幅值在较高值范围内增大时，簇间频率可能出现减小趋势。这些结论均为经颅磁声刺激的临床和实验研究提供了选定磁感应强度和超声强度调整范围的依据。同样由经颅磁声刺激表达式(1)可知，超声频率的变化会引起刺激交变电流频率的变化。由分析可知，当超声频率保持为10 kHz的整数倍时，无论其如何变化，均不会对分数阶扩展HR神经元的放电特性产生影响。否则，不仅会改变神经元的放电模式和放电节律，还会使得神经元膜电势在负电位值时发生高频率波动。因此，若要避免超声频率引发神经元放电特性的改变，在选取超声频率时，应尽可能选择10 kHz的整数倍为选定参数。
此外，本文对比了经颅磁声参数对分数阶与整数阶扩展HR神经元放电特性的影响，发现相比整数阶模型，分数阶模型在不同磁声参数下具有更多变的放电模式和更复杂的放电特性，这也进一步说明分数阶神经元模型在描述神经元放电特性方面更具普遍性和适应性。通过上述分析研究磁声刺激参数与具有更真实生物特性的大脑神经元模型放电特性的关系，有助于进一步理解经颅磁声刺激的影响机制，丰富经颅磁声刺激进入临床实验的理论依据。此外，针对具有磁声刺激输入的分数阶扩展HR神经元模型的动态特性分析，可作为计算神经科学和神经形态学的准备工作，为研究在人体大脑中很难识别的神经元之间的实际相互作用提供了模型基础。
-
[1] 袁毅, 庞娜, 陈玉东, 等. 经颅磁声刺激作用下神经元放电频率适应性的研究[J]. 生物医学工程学杂志, 2017, 34(6): 934–941.YUAN Yi, PANG Na, CHEN Yudong, et al. Study of neuronal spike-frequency adaptation with transcranial magneto-acoustical stimulation[J]. Journal of Biomedical Engineering, 2017, 34(6): 934–941. [2] 李江涛, 郑敏军, 曹辉. 经颅磁刺激技术的研究进展[J]. 高电压技术, 2016, 42(4): 1168–1178.LI Jiangtao, ZHENG Minjun, and CAO Hui. Research progress in transcranial magnetic stimulation technology[J]. High Voltage Engineering, 2016, 42(4): 1168–1178. [3] 于阳, 李玥, 张广浩, 等. 适用于临床及动物试验的高频重复经颅磁刺激系统设计及其应用[J]. 高电压技术, 2013, 39(1): 181–187. doi: 10.3969/j.issn.1003-6520.2013.01.026YU Yang, LI Yue, ZHANG Guanghao, et al. Design and application of high frequency repetitive transcranial magnetic stimulation system for clinical and animal tests[J]. High Voltage Engineering, 2013, 39(1): 181–187. doi: 10.3969/j.issn.1003-6520.2013.01.026 [4] 张帅, 史勋, 尹宁, 等. 基于H-H神经元模型的经颅磁声刺激对神经元放电活动的影响[J]. 高电压技术, 2019, 45(4): 1124–1130.ZHANG Shuai, SHI Xun, YIN Ning, et al. Effects of transcranial magneto-acoustical stimulation on neuronal firing activities based on H-H neuron model[J]. High Voltage Engineering, 2019, 45(4): 1124–1130. [5] WANG Yuexiang, FENG Lina, LIU Shikun, et al. Transcranial magneto-acoustic stimulation improves neuroplasticity in hippocampus of Parkinson’s disease model mice[J]. Neurotherapeutics, 2019, 16(4): 1210–1224. doi: 10.1007/s13311-019-00732-5 [6] ZHANG Shuai, CUI Kun, ZHANG Xueying, et al. Effect of transcranial ultrasonic-magnetic stimulation on two types of neural firing behaviors in modified izhikevich model[J]. IEEE Transactions on Magnetics, 2018, 54(3): 5000204. [7] NATARAJAN A and HASLER J. Hodgkin–Huxley neuron and FPAA dynamics[J]. IEEE Transactions on Biomedical Circuits and Systems, 2018, 12(4): 918–926. doi: 10.1109/TBCAS.2018.2837055 [8] YU Hongjie and PENG Jianhua. Chaotic synchronization and control in nonlinear-coupled Hindmarsh–Rose neural systems[J]. Chaos, Solitons & Fractals, 2006, 29(2): 342–348. [9] KUMAR D, SINGH J, and BALEANU D. A new numerical algorithm for fractional Fitzhugh–Nagumo equation arising in transmission of nerve impulses[J]. Nonlinear Dynamics, 2018, 91(1): 307–317. doi: 10.1007/s11071-017-3870-x [10] ERMENTROUT B. Linearization of F-I curves by adaptation[J]. Neural Computation, 1998, 10(7): 1721–1729. doi: 10.1162/089976698300017106 [11] TSUMOTO K, KITAJIMA H, YOSHINAGA T, et al. Bifurcations in Morris–Lecar neuron model[J]. Neurocomputing, 2006, 69(4/6): 293–316. [12] STOLIAR P, TRANCHANT J, CORRAZE B, et al. A leaky-integrate-and-fire neuron analog realized with a Mott Insulator[J]. Advanced Functional Materials, 2017, 27(11): 1604740. doi: 10.1002/adfm.201604740 [13] MOUJAHID A, D’ANJOU A, TORREALDEA F J, et al. Efficient synchronization of structurally adaptive coupled Hindmarsh–Rose neurons[J]. Chaos, Solitons & Fractals, 2011, 44(11): 929–933. [14] LÜ Mi, WANG Chunni, REN Guodong, et al. Model of electrical activity in a neuron under magnetic flow effect[J]. Nonlinear Dynamics, 2016, 85(3): 1479–1490. doi: 10.1007/s11071-016-2773-6 [15] LV Mi and MA Jun. Multiple modes of electrical activities in a new neuron model under electromagnetic radiation[J]. Neurocomputing, 2016, 205: 375–381. doi: 10.1016/j.neucom.2016.05.004 [16] VEPA R. Modelling and estimation of chaotic biological neurons[J]. IFAC Proceedings Volumes, 2009, 42(7): 27–32. doi: 10.3182/20090622-3-UK-3004.00008 [17] RECH P C. Dynamics in the parameter space of a neuron model[J]. Chinese Physics Letters, 2012, 29(6): 060506. doi: 10.1088/0256-307X/29/6/060506 [18] RAJAGOPAL K, KHALAF A J M, PARASTESH F, et al. Dynamical behavior and network analysis of an extended Hindmarsh–Rose neuron model[J]. Nonlinear Dynamics, 2019, 98(1): 477–487. doi: 10.1007/s11071-019-05205-0 [19] LUNDSTROM B N, HIGGS M H, SPAIN W J, et al. Fractional differentiation by neocortical pyramidal neurons[J]. Nature Neuroscience, 2008, 11(11): 1335–1342. doi: 10.1038/nn.2212 [20] ANASTASIO T J. The fractional-order dynamics of brainstem Vestibulo-Oculomotor Neurons[J]. Biological Cybernetics, 1994, 72(1): 69–79. doi: 10.1007/BF00206239 [21] DONG Jun, ZHANG Guangjun, XIE Yong, et al. Dynamic behavior analysis of fractional-order Hindmarsh–Rose neuronal model[J]. Cognitive Neurodynamics, 2014, 8(2): 167–175. doi: 10.1007/s11571-013-9273-x [22] XIE Yong, KANG Yanmei, LIU Yong, et al. Firing properties and synchronization rate in fractional-order Hindmarsh-Rose model neurons[J]. Science China Technological Sciences, 2014, 57(5): 914–922. doi: 10.1007/s11431-014-5531-3 [23] GIRESSE T A, CREPIN K T, and MARTIN T. Generalized synchronization of the extended Hindmarsh–Rose neuronal model with fractional order derivative[J]. Chaos, Solitons & Fractals, 2019, 118: 311–319. [24] YUAN Yi, PANG Na, CHEN Yudong, et al. A phase-locking analysis of neuronal firing rhythms with transcranial magneto-acoustical stimulation based on the Hodgkin-Huxley neuron model[J]. Frontiers in Computational Neuroscience, 2017, 11: 1. [25] YUAN Yi, CHEN Yudong, and LI Xiaoli. Theoretical analysis of transcranial magneto-acoustical stimulation with Hodgkin-Huxley neuron model[J]. Frontiers in Computational Neuroscience, 2016, 10: 35. [26] LIU Dan, ZHAO Song, LUO Xiaoyuan, et al. Unidirectional synchronization of Hodgkin-Huxley neurons with prescribed performance under transcranial magneto-acoustical simulation[J]. Frontiers in Neuroscience, 2019, 13: 1061. doi: 10.3389/fnins.2019.01061 [27] LIU Dan, ZHAO Song, LUO Xiaoyuan, et al. Synchronization for fractional-order extended Hindmarsh-Rose neuronal models with magneto-acoustical stimulation input[J]. Chaos, Solitons & Fractals, 2021, 144: 110635. [28] 汪芃, 李倩昀, 唐国宁. Hindmarsh-Rose神经元阵列自发产生螺旋波的研究[J]. 物理学报, 2018, 67(3): 030502. doi: 10.7498/aps.67.20172140WANG Peng, LI Qianyun, and TANG Guoning. Spontaneous generation of spiral wave in the array of Hindmarsh-Rose neurons[J]. Acta Physica Sinica, 2018, 67(3): 030502. doi: 10.7498/aps.67.20172140 [29] MENG Fanqi, ZENG Xiaoqin, and WANG Zuolei. Dynamical behavior and synchronization in time-delay fractional-order coupled neurons under electromagnetic radiation[J]. Nonlinear Dynamics, 2019, 95(2): 1615–1625. doi: 10.1007/s11071-018-4648-5 期刊类型引用(3)
1. 熊林海，吴朝俊，徐楚岩. 基于分数阶双忆阻器的多稳态混沌系统及其FPGA实现. 固体电子学研究与进展. 2024(01): 77-83 . 
百度学术2. 郭苗苗，翟昊迪，吉利辉，王田，徐桂芝. 经颅磁刺激对老年大鼠工作记忆相关跨脑区网络协同作用的影响. 电子与信息学报. 2024(04): 1468-1478 . 
本站查看3. 张帅，王艺潇，武健康，芈金睿，李子春，徐桂芝. 经颅磁声电刺激对老年小鼠电压门控钠钾离子通道的影响. 中国组织工程研究. 2023(26): 4200-4207 . 百度学术其他类型引用(5)
-
下载:
下载:
百度学术
计量
- 文章访问数: 876
- HTML全文浏览量: 582
- PDF下载量: 84
- 被引次数: 8
下载:
