基于改进贝叶斯非负Tikhonov正则化方法的同轴电缆信号传输畸变补偿研究

秦风; 高原; 吴双

doi:10.11999/JEIT210068

基于改进贝叶斯非负Tikhonov正则化方法的同轴电缆信号传输畸变补偿研究

doi: 10.11999/JEIT210068

1.
中国工程物理研究院应用电子学研究所绵阳 621900
2.
中国工程物理研究院复杂电磁环境科学与技术重点实验室绵阳 621900

基金项目: 中国工程物理研究院复杂电磁环境科学与技术重点实验室基金项目(FZSYS-02)

详细信息

作者简介:
秦风：男，1985年生，副研究员，研究方向为电磁脉冲环境测试、电磁环境效应及防护

高原：男，1989年生，助理研究员，研究方向为电磁脉冲环境仿真与测试

吴双：男，1993年生，初级工，研究方向为电磁环境测试

通讯作者:
高原　18142550916@163.com

中图分类号: O441.5; TM935.4
计量
- 文章访问数: 1026
- HTML全文浏览量: 366
- PDF下载量: 49
- 被引次数: 0
出版历程
- 收稿日期: 2021-01-18
- 修回日期: 2021-03-31
- 网络出版日期: 2021-04-16
- 刊出日期: 2021-08-10

Signal Compensation of Coaxial Cable Based on Modified Non-negative Tikhonov Regularization Method within Bayesian Inference

1.
Institute of Applied Electronics, China Academy of Engineering Physics, Mianyang 621900, China
2.
Key Laboratory of Science and Technology on Complex Electromagnetic Environment, China Academy of Engineering Physics, Mianyang 621900, China

Funds: Foundation of Key Laboratory of Science and Technology on Complex Electromagnetic Environment, China Academy of Engineering Physics (FZSYS-02)

摘要

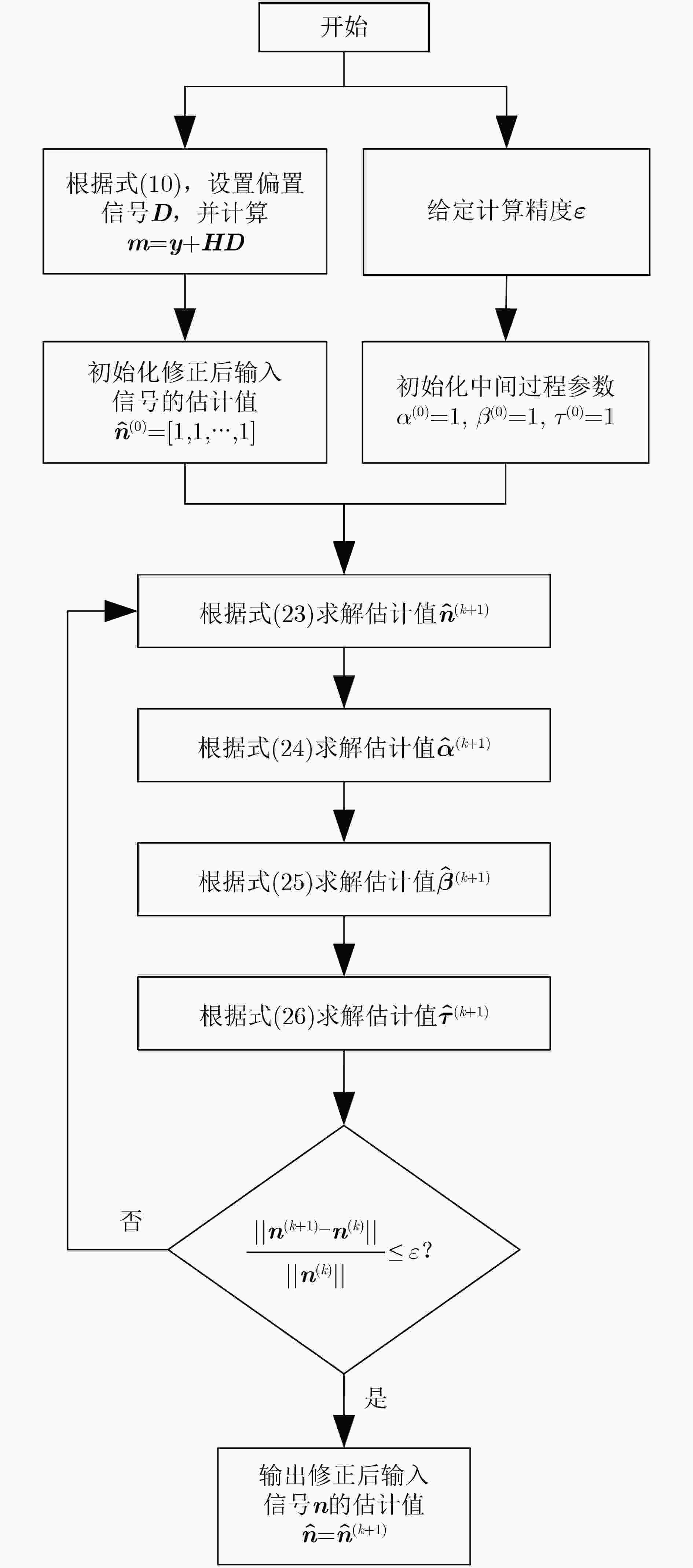
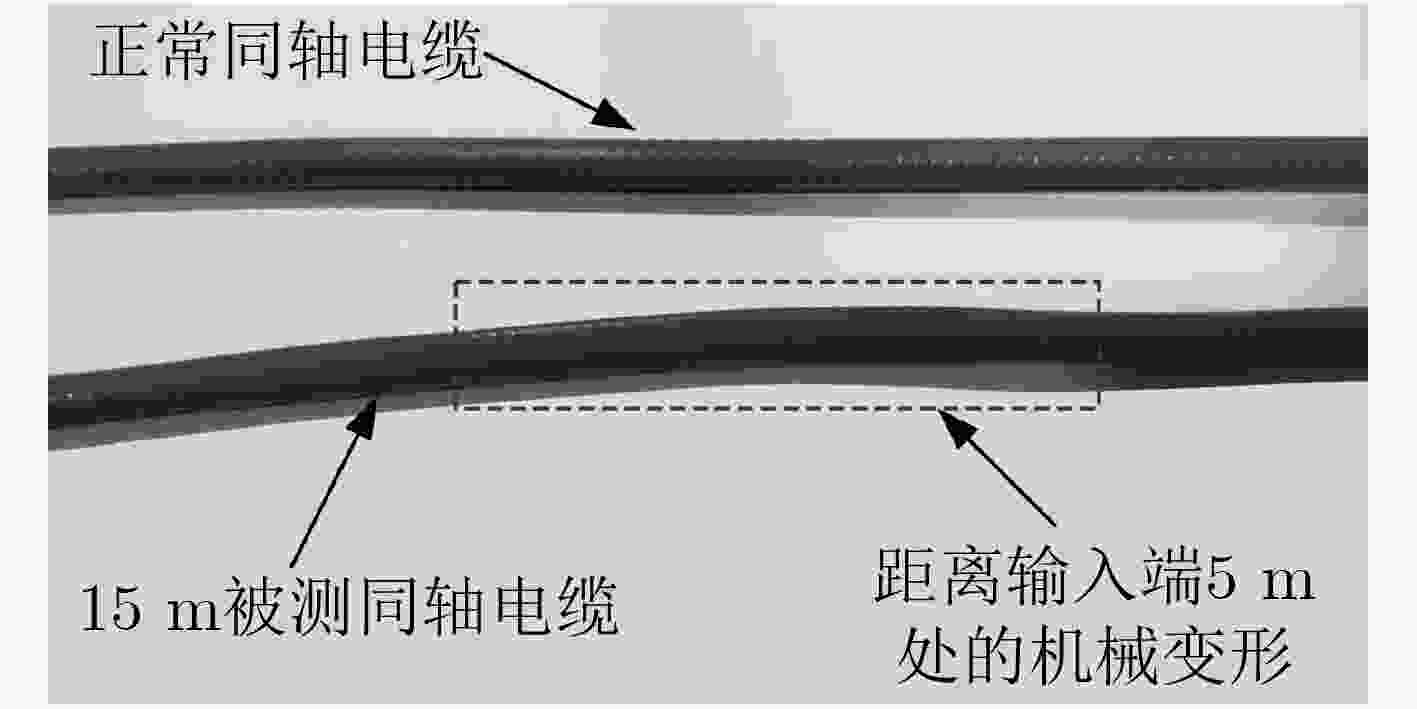
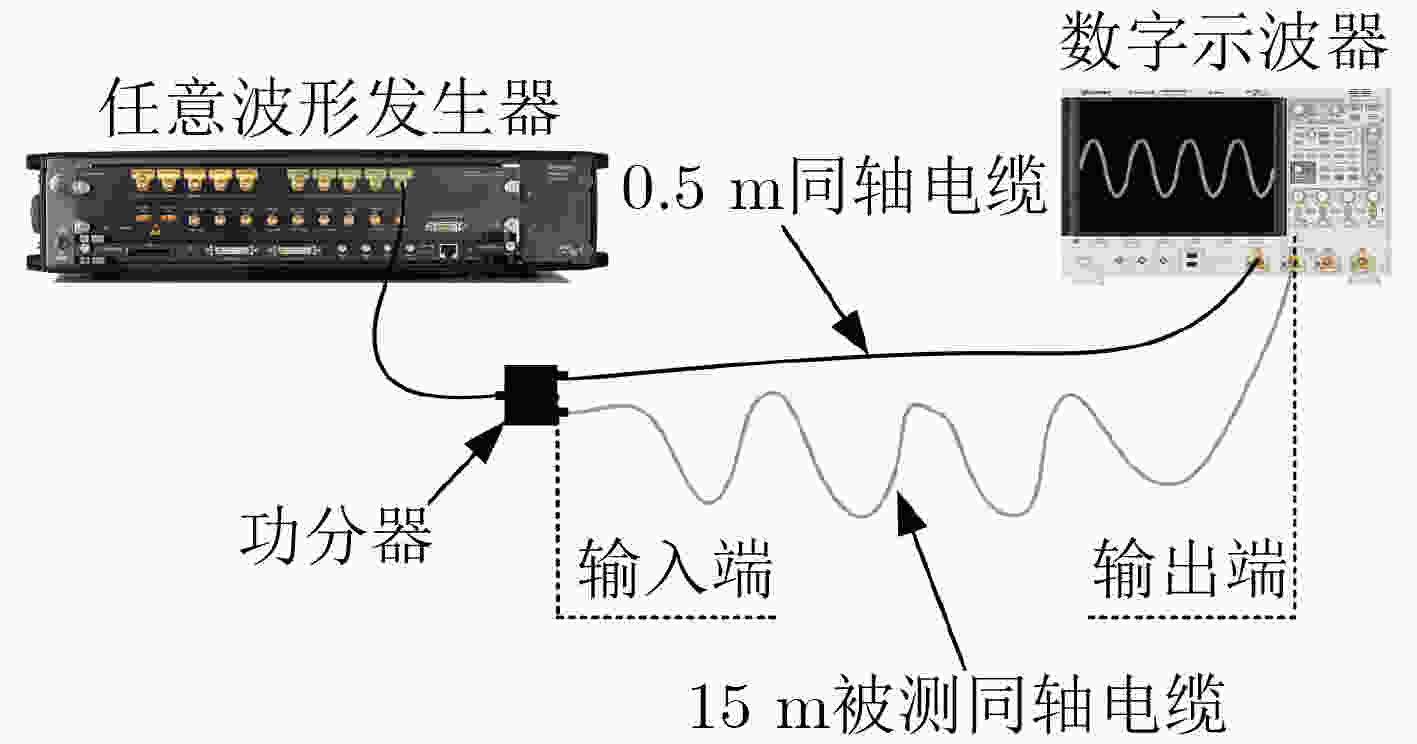
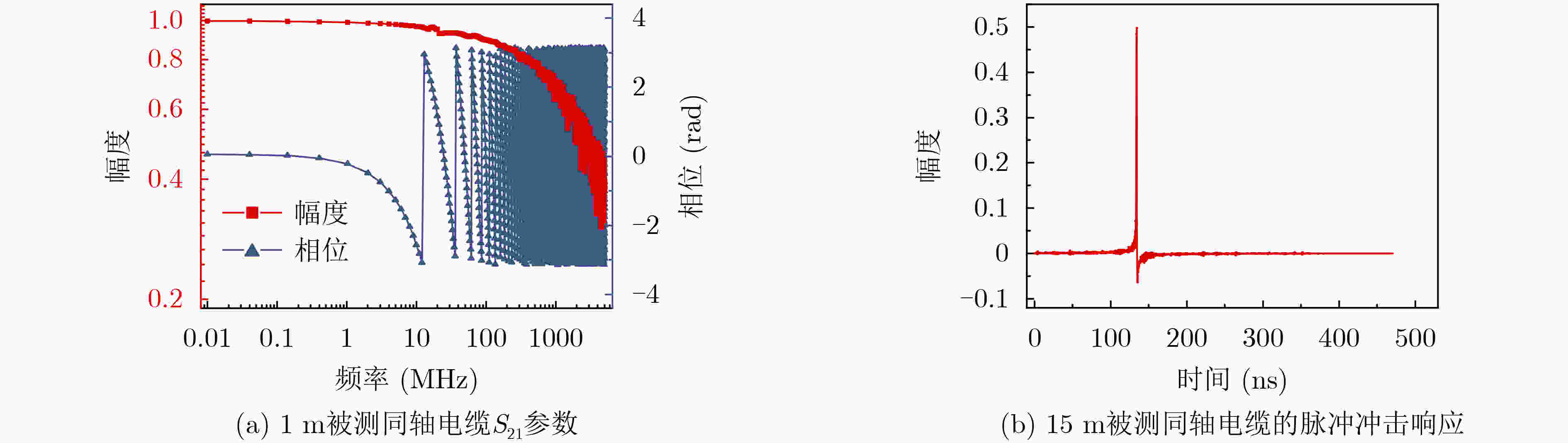
摘要: 随着信号频率、带宽及传输距离的增大，信号在同轴电缆传输过程中的畸变问题变得越来越严重。特别地，如果同轴电缆在使用过程中还意外地遭受了挤压、拉伸或折叠，信号畸变问题将会变得更加严重。该文基于贝叶斯推理的非负Tikhonov正则化方法，提出一种改进的信号补偿方法。该方法可有效规避逆分析中的病态矩阵问题，利用同轴电缆的冲击响应函数，并结合输出端口的测量信号，即可实现输入信号的重构。并以长度15 m的受挤压同轴电缆为对象，采用此方法对3种不同样式的脉冲信号(双指数脉冲信号、调制方波信号、双极脉冲信号)进行了传输畸变补偿。结果表明：该方法均能实现优异的补偿效果，补偿后信号与输入信号间偏差远远低于传统的衰减补偿法。并且，该方法具有较强的鲁棒性，当信噪比大于30 dB时，即可保持好的稳定性。
- 信号补偿 /
- 改进的非负Tikhonov正则化方法 /
- 同轴电缆
Abstract: With the increase of signal frequency, bandwidth and transmission distance, the signal distortion problem brought by the coaxial cable becomes serious and can not be ignored. Specifically, if the coaxial cable is accidentally squeezed, stretched or folded during use, the signal distortion problem will become more serious. Herein, a modified signal compensation method is proposed based on the non-negative Tikhonov regularization method with Bayesian inference. This method can effectively avoid the ill-conditioned matrix problem in the inverse analysis. The input signal can be reconstructed by using impulse response function of coaxial cable and measured output signal. Three different types of pulse signals, i.e., double exponential pulse signal, modulated square wave signal, and bipolar pulse signal, transmitted in a 15 m extruded coaxial cable are compensated. The results show that this method can achieve excellent compensation effect, and the deviation between the compensated signal and the input signal is far lower than that of typical attenuation compensation method. Moreover, the modified method exhibits strong robustness. When the signal-to-noise ratio is larger than 30 dB, it can maintain good stability.
- Signal compensation /
- Modified non-negative Tikhonov regularization method /
- Coaxial cable

HTML全文

1. 引言

随着雷达分辨率的不断提升，海杂波呈现出明显的重拖尾和非高斯特征，不再满足中心极限定理的假设，导致高斯杂波背景下设计的检测器虚警和漏检概率升高^[1]。复合高斯模型(Compound Gaussian Model, CGM)将高分辨海杂波建模为慢变纹理分量调制快变散斑分量的过程，能够较好地拟合高分辨海杂波的非高斯特性。利用不同分布的随机变量建模CGM的纹理分量即可得到不同的杂波模型。当纹理分量分别服从伽马分布、逆伽马分布和逆高斯(Inverse Gaussian, IG)分布时，海杂波幅度序列的概率密度函数(Probability Density Function, PDF)分别服从K分布^[2]，Pareto分布^[3]和逆高斯纹理复合高斯模型(Compound Gaussian model with Inverse Gaussian texture, CG-IG)^[4]。然而，受海况、擦地角、雷达极化方式和载频等因素的影响，上述3种杂波模型的拟合适用范围仍然存在限制，且存在模型选择问题。针对此问题，文献[5]提出使用广义逆高斯(Generalized Inverse Gaussian, GIG)分布建模CGM的纹理分量，得到具有高泛化能力和高拟合优度的广义逆高斯纹理复合高斯模型(Compound-Gaussian model with Generalized Inverse Gaussian texture, CG-GIG)。由于伽马分布、逆伽马分布和IG分布分别是GIG在不同参数下的特例，所以在GIG纹理背景下设计的相干检测器能够最大程度避免因拟合误差造成的性能损失。

为了解决非高斯、时变杂波背景下的目标检测问题，文献[6]首次在CGM下提出纹理分量未知的归一化自适应匹配滤波(Adaptive Normalized Matched Filter, ANMF)检测器。ANMF检测器虽然适用于所有纹理结构的复合高斯杂波，但其对任意一种纹理结构的杂波均不具有最优检测性能。针对伽马纹理结构下的K分布杂波，文献[7]基于GLRT准则，提出了最优K检测器(Optimum K Detector, OKD)。针对逆伽马纹理结构下的广义Pareto分布，文献[8]提出了广义似然比线性门限检测器(Generalized Likelihood Ratio Test with Linear-Threshold Detector, GLRT-LTD)。值得注意的是，GLRT-LTD为广义Pareto分布下的最优相干检测器，且具有解析的门限结构。文献[9]在CG-IG杂波背景下，基于GLRT准则设计具有逆高斯纹理结构的广义似然比(Generalized Likelihood Ratio Test with Inverse Gaussian texture, GLRT-IG)检测器。文献[10]给出了CG-GIG杂波背景下的最优相干检测器，命名为GIG纹理下的广义似然比检测(Generalized Likelihood Ratio Test with Generalized Inverse Gaussian texture, GIG-GLRT)器。为了进一步提升检测器的性能，海杂波的频谱分布、纹理分量空间相关性和散斑协方差矩阵斜对称特征等先验信息被引入检测器的结构设计。文献[11]结合ANMF检测器，在CG-GIG杂波背景下提出近最优的alpha自适应匹配滤波(α Adaptive Matched Filter, α-AMF)检测器，实现了检测性能和计算复杂度的折衷。文献[12]将海杂波纹理分量的空间相关性引入GLRT检测器的设计，在均匀和部分均匀杂波背景下提升了目标检测性能。文献[13]将协方差矩阵的斜对称特性引入检测器设计中，一定程度上降低了检测器对参考单元杂波数据的依赖。然而，上述检测器均假定目标速度已知，并未考虑导向矢量失配对检测器的影响。在实际雷达对海探测过程中，受波束指向误差等不确定性因素的影响，实际导向矢量和理论导向矢量可能存在不匹配现象，如图1所示。导向矢量的失配可能会检测到非期望的副瓣目标，从而引起不必要的虚警。为了平衡检测器的目标检测性能以及抗失配能力，文献[14]在存在失配信号的条件下推导得到自适应波束形成器正交抑制检测(Adaptive Beamformer Orthogonal Rejection Test, ABORT)算法。文献[15]在CG-IG分布杂波背景下，提出类似于ABORT检测器结构的目标检测算法。针对距离扩展目标检测问题，文献[16]在K分布杂波背景下设计类似于ABORT的检测器。

图 1 失配示意图

下载: 全尺寸图片幻灯片

本文针对GIG纹理背景下的失配检测问题，分别基于GLRT和最大后验估计GLRT(Maximum A Posteriori GLRT, MAP GLRT)准则发展类似于ABORT的失配检测器。首先，通过在零假设中引入与理论导向矢量正交的虚拟信号来抑制失配信号。然后基于失配情况下的目标检测模型设计两个失配检测器，并证明其对散斑协方差矩阵和目标多普勒导向矢量均具有CFAR特性。最后仿真和实测海杂波数据实验结果表明，提出的失配检测器以牺牲匹配情况下较小的检测性能为代价，换取了较高的抗失配性能。相较于CG-GIG分布下的GIG-GLRT, MAP-GLRT^[17], α-AMF检测器以及不依赖纹理结构分布的ANMF和ABORT检测器，提出的失配检测器同时兼备较好的目标检测性能和抗失配性能。

2. 失配信号的目标检测模型

失配情况下的实际导向矢量 ${{\boldsymbol p}_{\mathrm{m}}}$ 通常由平行和正交于理论导向矢量 ${\boldsymbol{p}}$ 的 ${\boldsymbol p}_{\mathrm{m}}^\parallel$ 和 ${\boldsymbol p}_{\mathrm{m}}^ \bot$ 构成，即 ${{\boldsymbol p}_{\mathrm{m}}} = {\boldsymbol p}_{\mathrm{m}}^\parallel + {\boldsymbol p}_{\mathrm{m}}^ \bot$ 。其中， ${\boldsymbol p}_{\mathrm{m}}^\parallel = \alpha {\boldsymbol{p}}$ 是希望检测到的目标回波，而 ${\boldsymbol p}_{\mathrm{m}}^ \bot = \beta {\boldsymbol{q}}$ 是不希望检测到的干扰信号。为了提升检测器的抗失配性能，与ABORT检测器类似，引入虚拟信号 $\beta {\boldsymbol{q}}$ 建模零假设 ${H_0}$ 下的待检测(Cell Under Test, CUT)回波向量。因此在GIG纹理背景下导向矢量失配的目标检测模型定义为

$\left. {\begin{array}{*{20}{c}} {{H_0}:\left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{z}} = \beta {\boldsymbol{q}} + {\boldsymbol{c}}} \\ {{{\boldsymbol{z}}_k} = {{\boldsymbol{c}}_k},k = 1,2, \cdots ,L} \end{array}} \right.} \\ {{H_1}:\left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{z}} = \alpha {\boldsymbol{p}} + {\boldsymbol{c}}} \\ {{{\boldsymbol{z}}_k} = {{\boldsymbol{c}}_k},k = 1,2, \cdots ,L} \end{array}} \right.} \end{array}} \right\}$

(1)

其中，零假设 ${H_0}$ 表示CUT中不存在目标，而备择假设 ${H_1}$ 表示CUT中存在目标。向量 ${\boldsymbol{z}} = {\left[ {{z_1},{z_2}, \cdots ,{z_N}} \right]^{\mathrm{T}}}$ 表示CUT回波，其中包含 $N$ 个相参脉冲； ${{\boldsymbol{z}}_k},k = 1,2, \cdots ,L$ 表示CUT周围存在的 $L$ 个参考单元； $\alpha$ 表示目标回波幅度，通常被建模为Swerling 0型； ${\boldsymbol{p}} = \left[ {1,{{\mathrm{e}}^{{\mathrm{j}}2\pi {f_{\mathrm{d}}}}}, \cdots ,{{\mathrm{e}}^{{\mathrm{j}}2\pi \left( {N - 1} \right){f_{\mathrm{d}}}}}} \right]$ 表示目标回波的导向矢量，其归一化多普勒频率 ${f_{\mathrm{d}}}$ 在区间 $\left[ { - 0.5,0.5} \right]$ 内服从均匀分布； $\tau$ 和 ${{u}}$ 分别表示杂波的纹理分量和散斑分量； $\beta {\boldsymbol{q}}$ 表示人为引入 ${H_0}$ 的虚拟信号， $\beta$ 和 ${\boldsymbol{q}}$ 分别表示虚拟信号的复幅度和导向矢量，虚拟导向矢量 ${\boldsymbol{q}}$ 在白化空间中与理论导向矢量 ${\boldsymbol{p}}$ 正交，即 $\left\langle {{{\boldsymbol{M}}^{ - 1/2}}{\boldsymbol{p}}} \right\rangle = {\left\langle {{{\boldsymbol{M}}^{ - 1/2}}{\boldsymbol{q}}} \right\rangle ^ \bot }$ 。需要注意的是，在ABORT检测器中，所引入的虚拟信号 ${\boldsymbol{q}}$ 与理论导向矢量 ${\boldsymbol{p}}$ 在准白化空间中正交，即 $\left\langle {{{\boldsymbol{S}}^{ - 1/2}}{\boldsymbol{p}}} \right\rangle = {\left\langle {{{\boldsymbol{S}}^{ - 1/2}}{\boldsymbol{q}}} \right\rangle ^ \bot }$ ，其中 ${\boldsymbol{S}}$ 表示理论散斑协方差矩阵 ${\boldsymbol{M}}$ 的估计值。根据球不变随机向量模型，CUT回波向量在 ${H_0}$ 和 ${H_1}$ 假设下的条件PDF定义为

$\begin{split} \,&{f_0}\left( {{\boldsymbol{z}}|\beta ,{\boldsymbol{M}},\tau ;{H_0}} \right) = \frac{1}{{{{\left( {\pi \tau } \right)}^N}\left| {\boldsymbol{M}} \right|}}\\ & \qquad \cdot \exp \left( { - \frac{{{{\left( {{\boldsymbol{z}} - \beta {\boldsymbol{q}}} \right)}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}\left( {{\boldsymbol{z}} - \beta {\boldsymbol{q}}} \right)}}{\tau }} \right) \end{split}$

(2)

$\begin{split} & {f_1}\left( {{\boldsymbol{z}}|\alpha ,{\boldsymbol{M}},\tau ;{H_1}} \right) = \frac{1}{{{{\left( {\pi \tau } \right)}^N}\left| {\boldsymbol{M }}\right|}}\\ & \qquad \cdot\exp \left( { - \frac{{{{\left( {{\boldsymbol{z}} - \alpha {\boldsymbol{p}}} \right)}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}\left( {{\boldsymbol{z}} - \alpha {\boldsymbol{p}}} \right)}}{\tau }} \right) \end{split}$

(3)

其中， $\tau$ 表示GIG分布的随机数，其PDF表达式 $f\left( \tau \right)$ 为

$f\left( \tau \right) = \frac{{{{\left( {a/b} \right)}^{p/2}}{\tau ^{p - 1}}}}{{2{K_p}\left( {\sqrt {ab} } \right)}}{{\mathrm{e}}^{ - \frac{{\left( {a\tau + b/\tau } \right)}}{2}}},a \gt 0,b \gt 0$

(4)

其中， $a$ 和 $b$ 分别表示GIG分布的形状参数和尺度参数， ${K_p}\left( \cdot \right)$ 表示 $p$ 阶第2类修正Bessel函数。伽马和逆伽马分布分别对应形状参数 $a = 0$ 和尺度参数 $b = 0$ 时的GIG分布；当 $p = - {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}$ , $b = \lambda u$ 和 $a = {\lambda \mathord{\left/ {\vphantom {\lambda u}} \right. } u}$ 时，GIG分布退化为形状参数为 $\lambda$ 尺度参数为 $\mu$ 的GIG分布。

3. 基于GIG纹理结构的失配检测器

本节考虑导向矢量失配的影响，基于两步GLRT和MAP-GLRT准则在广义逆高斯杂波背景下设计失配检测器，并通过理论证明所提检测器对散斑协方差矩阵 ${\boldsymbol{M}}$ 以及目标多普勒导向矢量 ${\boldsymbol{p}}$ 具有CFAR特性。

3.1 GLRT准则下的失配检测器

本节基于两步GLRT准则设计失配检测器。首先假设杂波散斑分量 ${{u}}$ 的协方差矩阵 ${\boldsymbol{M}}$ 已知，那么导向矢量失配情况下的GLRT准则定义为

$\frac{{\mathop {\max }\limits_\alpha \displaystyle\int {{f_1}\left( {{\boldsymbol{z}}|\alpha ,\tau ;{H_1}} \right)f\left( \tau \right){\mathrm{d}}\tau } }}{{\mathop {\max }\limits_\beta \displaystyle\int {{f_0}\left( {{\boldsymbol{z}}|\beta ,\tau ;{H_0}} \right)f\left( \tau \right){\mathrm{d}}\tau } }}\mathop \gtrless \limits_{{H_0}}^{{H_1}} {\xi _{\mathrm{g}}}$

(5)

其中， ${\xi _{\mathrm{g}}}$ 为GLRT检测器的检测门限，式(5)中参数 $\alpha$ 和 $\beta$ 的最大似然(Maximum Likelihood, ML)估计为 $\hat \alpha$ 与 $\hat \beta$ ，定义分别为

$\hat \alpha = \frac{{{{\boldsymbol{p}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{z}}}}{{{{\boldsymbol{p}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{p}}}}$

(6)

$\hat \beta = \frac{{{{\boldsymbol{q}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{z}}}}{{{{\boldsymbol{q}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{q}}}}$

(7)

将式(6)和式(7)分别代入式(2)和式(3)的条件PDF中，可以得到

$\begin{split} \mathop {\max }\limits_\beta {f_0}\left( {{\boldsymbol{z}}|\beta ,\tau ;{H_0}} \right) = \,& {f_0}\left( {{\boldsymbol{z}}|\hat \beta ,\tau ;{H_0}} \right) = \frac{1}{{{{\left( {\pi \tau } \right)}^N}\left| {\boldsymbol{M}} \right|}}\\ & \cdot\exp \left( { - \frac{{{l_0}}}{\tau }} \right)\\[-1pt] \end{split}$

(8)

$\begin{split} \mathop {\max }\limits_\alpha {f_1}\left( {{\boldsymbol{z}}|\alpha ,\tau ;{H_1}} \right) =\,& {f_0}\left( {{\boldsymbol{z}}|\hat \alpha ,\tau ;{H_1}} \right) = \frac{1}{{{{\left( {\pi \tau } \right)}^N}\left| {\boldsymbol{M}} \right|}}\\ & \cdot \exp \left( { - \frac{{{l_1}}}{\tau }} \right) \\[-1pt] \end{split}$

(9)

其中 ${l_0}$ 和 ${l_1}$ 分别定义为

${l_0} = {{\boldsymbol{z}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{z}} - \frac{{{{\left| {{{\boldsymbol{q}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{z}}} \right|}^2}}}{{{{\boldsymbol{q}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{q}}}}$

(10)

${l_1} = {{\boldsymbol{z}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{z}} - \frac{{{{\left| {{{\boldsymbol{p}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{z}}} \right|}^2}}}{{{{\boldsymbol{p}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{p}}}}$

(11)

设矩阵 ${\boldsymbol{A}}$ 的投影矩阵为 ${{\boldsymbol{P}}_{\boldsymbol{A}}} = {\boldsymbol{A}}{\left( {{{\boldsymbol{A}}^{\mathrm{H}}}{\boldsymbol{A}}} \right)^{ - 1}}{{\boldsymbol{A}}^{\mathrm{H}}}$ ，那么投影矩阵 ${{\boldsymbol{P}}_{\boldsymbol{A}}}$ 的正交补矩阵定义为 ${\boldsymbol{P}}_{\boldsymbol{A}}^ \bot = {\boldsymbol{I}} - {{\boldsymbol{P}}_{\boldsymbol{A}}} = {\boldsymbol{I}} - {\boldsymbol{A}}{\left( {{{\boldsymbol{A}}^{\mathrm{H}}}{\boldsymbol{A}}} \right)^{ - 1}}{{\boldsymbol{A}}^{\mathrm{H}}}$ ，其中 ${\boldsymbol{I}}$ 表示与矩阵 ${\boldsymbol{A}}$ 行维数相同的单位矩阵。利用虚拟导向矢量 ${\boldsymbol{q}}$ 与理论导向矢量 ${\boldsymbol{p}}$ 在白化空间中相互正交的性质， $\left\langle {{{\boldsymbol{M}}^{ - 1/2}}{\boldsymbol{p}}} \right\rangle = {\left\langle {{{\boldsymbol{M}}^{ - 1/2}}{\boldsymbol{q}}} \right\rangle ^ \bot }$ 可以改写为

${{\boldsymbol{I}}_N} - \frac{{{{\boldsymbol{M}}^{ - 1/2}}{\boldsymbol{q}}{{\boldsymbol{q}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1/2}}}}{{{{\boldsymbol{q}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{q}}}} = \frac{{{{\boldsymbol{M}}^{ - 1/2}}{\boldsymbol{p}}{{\boldsymbol{p}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1/2}}}}{{{{\boldsymbol{p}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{p}}}}$

(12)

将式(12)代入式(10)，化简 ${l_0}$ 为

$\begin{split} {l_0} \,& = {{\boldsymbol{z}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1/2}}\left( {{{\boldsymbol{I}}_N} - \frac{{{{\boldsymbol{M}}^{ - 1/2}}{\boldsymbol{q}}{{\boldsymbol{q}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1/2}}}}{{{{\boldsymbol{q}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{q}}}}} \right){{\boldsymbol{M}}^{ - 1/2}}{\boldsymbol{z}} \\ & = \frac{{{{\left| {{{\boldsymbol{p}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{z}}} \right|}^2}}}{{{{\boldsymbol{p}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{p}}}}\\[-1pt] \end{split}$

(13)

将式(4)和式(9)代入式(5)，即可得到式(5)分子部分关于纹理分量 $\tau$ 的积分结果，如式(14)所示

$\begin{split} \int {{f_1}\left( {{\boldsymbol{z}}|\hat \alpha ,\tau ;{H_1}} \right)f\left( \tau \right){\mathrm{d}}\tau } =\,& \frac{{{a^{{N / 2}}}{b^{ - {p / 2}}}{{\left( {2{l_1} + b} \right)}^{\frac{{p - N}}{2}}}}}{{{\pi ^N}\left| {\boldsymbol{M}} \right| {K_p}\left( {\sqrt {ab} } \right)}}\\ & \cdot{K_{N - p}}\left( {\sqrt {a\left( {2{l_1} + b} \right)} } \right) \end{split}$

(14)

同理，式(5)分母部分关于纹理分量 $\tau$ 的积分结果如式(15)所示

$\begin{split} \int {{f_0}\left( {{\boldsymbol{z}}|\hat \beta ,\tau ;{H_0}} \right)f\left( \tau \right){\mathrm{d}}\tau } =\,& \frac{{{a^{{N / 2}}}{b^{ - {p / 2}}}{{\left( {2{l_0} + b} \right)}^{\frac{{p - N}}{2}}}}}{{{\pi ^N}\left| {\boldsymbol{M}} \right|{K_p}\left( {\sqrt {ab} } \right)}}\\ & \cdot {K_{N - p}}\left( {\sqrt {a\left( {2{l_0} + b} \right)} } \right) \end{split}$

(15)

将式(14)和式(15)代入式(5)，即可得到广义逆高斯纹理复合高斯杂波背景下类似于AOBRT(ABORT-like Generalized Compound Gaussian with Inverse Gaussian, A-CGGIG)检测器的检验统计量，如式(16)所示

$\frac{{{{\left( {2{l_1} + b} \right)}^{\frac{{P - N}}{2}}}{K_{N - p}}\left( {\sqrt {a\left( {2{l_1} + b} \right)} } \right)}}{{{{\left( {2{l_0} + b} \right)}^{\frac{{P - N}}{2}}}{K_{N - p}}\left( {\sqrt {a\left( {2{l_0} + b} \right)} } \right)}}\mathop \gtrless \limits_{{H_0}}^{{H_1}} {\xi _{\mathrm{g}}}$

(16)

第2步，利用参考单元数据 ${{\boldsymbol{z}}_k},k = 1,2, \cdots ,L$ 估计散斑分量的协方差矩阵实现自适应相干检测。本文采用约束渐进最大似然估计器(Constrained Approximate Maximum Likelihood Estimator, CAMLE)估计 ${\boldsymbol{M}}$ ，降低海杂波纹理分量 $\tau$ 对散斑协方差矩阵估计的影响，CAMLE的定义为

$\left. \begin{aligned} & {\hat {\boldsymbol{M}}\left( m \right) = \frac{N}{L}\sum\limits_{k = 1}^L {\frac{{{{\boldsymbol{z}}_k}{\boldsymbol{z}}_k^{\mathrm{H}}}}{{{\boldsymbol{z}}_k^{\mathrm{H}}{{\hat {\boldsymbol{M}}}^{ - 1}}\left( m \right){{\boldsymbol{z}}_k}}}} } \\ & {\hat {\boldsymbol{M}}\left( m \right) = \frac{N}{{{\mathrm{Tr}}\left( {\hat {\boldsymbol{M}}\left( m \right)} \right)}}{{\hat {\boldsymbol{M}}}_{{\mathrm{CAMLE}}}}\left( {{m}} \right)} \end{aligned} \right\}$

(17)

其中， $m$ 表示迭代次数，运算符 ${\mathrm{Tr}}\left( \cdot \right)$ 表示求矩阵的迹。CAMLE的初值通常采用归一化样本协方差矩阵(Normalized Sample Covariance Matrix, NSCM)，通过1～3次迭代即可得到较为准确的估计结果。将散斑协方差矩阵的估计结果 $\hat {\boldsymbol{M}}$ 带入式(16)，得到自适应的A-CGGIG检测器

$\frac{{{{\left( {2{{\hat l}_1} + b} \right)}^{\frac{{P - N}}{2}}}{K_{N - p}}\left( {\sqrt {a\left( {2{{\hat l}_1} + b} \right)} } \right)}}{{{{\left( {2{{\hat l}_0} + b} \right)}^{\frac{{P - N}}{2}}}{K_{N - p}}\left( {\sqrt {a\left( {2{{\hat l}_0} + b} \right)} } \right)}}\mathop \gtrless \limits_{{H_0}}^{{H_1}} {\xi _{\mathrm{g}}}$

(18)

其中， ${\hat l_1}$ 和 ${\hat l_0}$ 分别是 ${l_1}$ 和 ${l_0}$ 的估计值，定义为

$\left. \begin{aligned} & {{{\hat l}_1} = {{\boldsymbol{z}}^{\mathrm{H}}}{{\hat {\boldsymbol{M}}}^{ - 1}}{\boldsymbol{z}} - {{\left| {{{\boldsymbol{p}}^{\mathrm{H}}}{{\hat {\boldsymbol{M}}}^{ - 1}}{\boldsymbol{z}}} \right|}^2}/\left( {{{\boldsymbol{p}}^{\mathrm{H}}}{{\hat {\boldsymbol{M}}}^{ - 1}}{\boldsymbol{p}}} \right)} \\ & {{{\hat l}_0} = {{\left| {{{\boldsymbol{p}}^{\mathrm{H}}}{{\hat {\boldsymbol{M}}}^{ - 1}}{\boldsymbol{z}}} \right|}^2}/\left( {{{\boldsymbol{p}}^{\mathrm{H}}}{{\hat {\boldsymbol{M}}}^{ - 1}}{\boldsymbol{p}}} \right)} \end{aligned} \right\}$

(19)

3.2 MAP GLRT准则下的失配检测器

本节基于两步MAP GLRT准则设计失配检测器。首先假设杂波散斑分量 ${{u}}$ 的协方差矩阵 ${\boldsymbol{M}}$ 已知，那么导向矢量失配情况下的MAP GLRT准则定义为

$\frac{{\mathop {\max }\limits_{{\tau _1},\alpha } {f_1}\left( {{\boldsymbol{z}}|\alpha ,{\tau _1};{H_1}} \right)f\left( \tau \right)}}{{\mathop {\max }\limits_{{\tau _0},\beta } {f_0}\left( {{\boldsymbol{z}}|\beta ,{\tau _0};{H_0}} \right)f\left( \tau \right)}}\mathop \gtrless \limits_{{H_0}}^{{H_1}} {\xi _{\mathrm{h}}}$

(20)

其中， ${\xi _{\mathrm{h}}}$ 表示MAP GLRT检测器的检测门限。参数 $\alpha$ 和 $\beta$ 的ML估计 $\hat \alpha$ 和 $\hat \beta$ 同式(6)和式(7)。将 $\hat \alpha$ 和 $\hat \beta$ 代入式(2)和式(3)，并乘以式(4)所示的广义逆高斯分布，即可得到式(21)和式(22)

$\begin{split} {f_0}\left( {{\boldsymbol{z}}|\hat \beta ,{\tau _0};{H_0}} \right)f\left( {{\tau _0}} \right) =\,& \frac{{{{\left( {a/b} \right)}^{p/2}}}}{{2{K_p}\left( {\sqrt {ab} } \right){\pi ^N}\left| {\boldsymbol{M}} \right|}}\tau _0^{p - N - 1}\\ & \cdot \exp \left[ { - \left( {\frac{a}{2}{\tau _0} + \frac{{{l_0} + {b \mathord{\left/ {\vphantom {b 2}} \right. } 2}}}{{{\tau _0}}}} \right)} \right] \end{split}$

(21)

$\begin{split} {f_1}\left( {{\boldsymbol{z}}|\hat \alpha ,{\tau _1};{H_1}} \right)f\left( {{\tau _1}} \right) =\,& \frac{{{{\left( {a/b} \right)}^{p/2}}}}{{2{K_p}\left( {\sqrt {ab} } \right){\pi ^N}\left| {\boldsymbol{M}} \right|}}\tau _1^{p - N - 1}\\ & \cdot\exp \left[ { - \left( {\frac{a}{2}{\tau _1} + \frac{{{l_1} + {b \mathord{\left/ {\vphantom {b 2}} \right. } 2}}}{{{\tau _1}}}} \right)} \right] \end{split}$

(22)

分别计算式(21)和式(22)的对数表达式，并对纹理分量 $\tau$ 求偏导，将其结果置0，即可以分别得到零假设 ${H_0}$ 和备择假设 ${H_1}$ 下纹理分量的MAP估计 ${\hat \tau _0}$ 和 ${\hat \tau _1}$ ，如式(23)和式(24)所示

$\begin{split} \quad\;\; {\hat \tau _0} = \,& \left( - \left( {N + 1 - p} \right) + {\mathrm{sqrt}}\Bigr( {{\left( {N + 1 - p} \right)}^2} \right.\\ & \left.+ a\left( {2{l_0} + b} \right) \Bigr) \right)/a \end{split}$

(23)

$\begin{split} \quad \;\; {\hat \tau _1} =\,& \left( - \left( {N + 1 - p} \right) + {\mathrm{sqrt}}\Bigr( {{\left( {N + 1 - p} \right)}^2} \right.\\ & \left. + a\left( {2{l_1} + b} \right) \Bigr) \right)/a \end{split}$

(24)

将式(11)、式(13)、式(23)和式(24)代入式(20)，即可得到基于MAP准则的广义逆高斯纹理复合高斯杂波背景下类似于AOBRT(ABORT-like Generalized Compound Gaussian with Inverse Gaussian, AM-CGGIG)检测器的检验统计量，如式(25)所示

$\frac{{{{\hat \tau }_1}^{p - N - 1}\exp \left[ { - \left( {\dfrac{a}{2}{{\hat \tau }_1} + \dfrac{{{l_1} + {b \mathord{\left/ {\vphantom {b 2}} \right. } 2}}}{{{{\hat \tau }_1}}}} \right)} \right]}}{{{{\hat \tau }_0}^{p - N - 1}\exp \left[ { - \left( {\dfrac{a}{2}{{\hat \tau }_0} + \dfrac{{{l_0} + {b \mathord{\left/ {\vphantom {b 2}} \right. } 2}}}{{{{\hat \tau }_0}}}} \right)} \right]}}\mathop \gtrless \limits_{{H_2}}^{{H_1}} {\xi _{\mathrm{h}}}$

(25)

第2步，将式(17)中的CAMLE的估计结果代入式(25)，即可得到AM-CGGIG检测器的自适应形式，定义为

$\frac{{{{\hat \tau }_1}^{p - N - 1}\exp \left[ { - \left( {\dfrac{a}{2}{{\hat \tau }_1} + \dfrac{{{{\hat l}_1} + {b \mathord{\left/ {\vphantom {b 2}} \right. } 2}}}{{{{\hat \tau }_1}}}} \right)} \right]}}{{{{\hat \tau }_0}^{p - N - 1}\exp \left[ { - \left( {\dfrac{a}{2}{{\hat \tau }_0} + \dfrac{{{{\hat l}_0} + {b \mathord{\left/ {\vphantom {b 2}} \right. } 2}}}{{{{\hat \tau }_0}}}} \right)} \right]}}\mathop \gtrless \limits_{{H_2}}^{{H_1}} {\xi _{\mathrm{h}}}$

(26)

对比式(18)和式(26)的检验统计量可以发现，次优的AM-CGGIG检测器由于利用MAP算法估计海杂波的纹理结构，其检验统计量中不存在第2类修正Bessel函数，因此降低了计算复杂度。

3.3 失配检测器的CFAR特性分析

本节分析提出的A-CGGIG和AM-CGGIG检测器的CFAR特性。可以发现式(18)和式(26)均为变量 ${\hat l_0}$ 和 ${\hat l_1}$ 的函数，因此仅需分析 ${\hat l_0}$ 和 ${\hat l_1}$ 与失配检测器的关系即可，首先将这两个变量分别重写为

${\hat l_0} = \frac{{{{\left| {{{\left( {{{\boldsymbol{M}}^{ - {1 / 2}}}{\boldsymbol{p}}} \right)}^{\mathrm{H}}}{{\boldsymbol{M}}^{{1 / 2}}}{{\hat M}^{ - 1}}{{\boldsymbol{M}}^{{1 / 2}}}\left( {{{\boldsymbol{M}}^{ - {1 / 2}}}{\boldsymbol{z}}} \right)} \right|}^2}}}{{{{\left( {{{\boldsymbol{M}}^{ - {1/ 2}}}{\boldsymbol{p}}} \right)}^{\mathrm{H}}}{{\boldsymbol{M}}^{{1/ 2}}}{{\hat {\boldsymbol{M}}}^{ - 1}}{{\boldsymbol{M}}^{{1 / 2}}}\left( {{{\boldsymbol{M}}^{ - {1 / 2}}}{\boldsymbol{p}}} \right)}}$

(27)

${\hat l_1} = {\left( {{{\boldsymbol{M}}^{ - {1 / 2}}}{\boldsymbol{z}}} \right)^{\mathrm{H}}}{{\boldsymbol{M}}^{{1 / 2}}}{\hat {\boldsymbol{M}}^{ - 1}}{{\boldsymbol{M}}^{{1 / 2}}}\left( {{{\boldsymbol{M}}^{ - {1 / 2}}}{\boldsymbol{z}}} \right) - {\hat l_0}$

(28)

对于重塑后的导向矢量 ${{\boldsymbol{M}}^{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. } 2}}}{\boldsymbol{p}}$ 而言，总存在一个Householder矩阵 ${\boldsymbol{P}}$ ，能够将其转化为 ${\boldsymbol{P}}{{\boldsymbol{M}}^{{{ - 1} / 2}}}{\boldsymbol{p}} = \left| {{{\boldsymbol{M}}^{{{ - 1} / 2}}}{\boldsymbol{p}}} \right|{\boldsymbol{v}}$ ，其中 ${\boldsymbol{v}} = {\left( {1,0,0, \cdots ,0} \right)^{\mathrm{T}}}$ 。基于球不变随机向量模型，分别化简 ${\hat l_0}$ 和 ${\hat l_1}$ 为

$\begin{split} & {\hat l_0} \\ & = \frac{{{{\left| {{{\left( {{\boldsymbol{P}}{{\boldsymbol{M}}^{ - {1 / 2}}}{\boldsymbol{p}}} \right)}^{\mathrm{H}}} {\boldsymbol{P}}{{\boldsymbol{M}}^{{1 / 2}}} {{\hat {\boldsymbol{M}}}^{ - 1}} {{\boldsymbol{M}}^{{1 / 2}}}{{\boldsymbol{P}}^{\mathrm{H}}} \left( {{\boldsymbol{P}}{{\boldsymbol{M}}^{ - {1 / 2}}}{\boldsymbol{z}}} \right)} \right|}^2}}}{{{{\left( {{\boldsymbol{P}}{{\boldsymbol{M}}^{ - {1 /2}}}{\boldsymbol{p}}} \right)}^{\mathrm{H}}}{\boldsymbol{P}}{{\boldsymbol{M}}^{{1 / 2}}}{{\hat{\boldsymbol{M}}}^{ - 1}} {{\boldsymbol{M}}^{{1 / 2}}}{{\boldsymbol{P}}^{\mathrm{H}}} \left( {{\boldsymbol{P}}{{\boldsymbol{M}}^{ - {1 / 2}}}{\boldsymbol{p}}} \right)}} \\ & = \tau \frac{{{{\left| {{{\boldsymbol{v}}^{\mathrm{H}}}{{\bar {\boldsymbol{M}}}^{ - 1}}{\boldsymbol{n}}} \right|}^2}}}{{{{\boldsymbol{v}}^{\mathrm{H}}}{{\bar {\boldsymbol{M}}}^{ - 1}}{\boldsymbol{v}}}}\\[-1pt] \end{split}$

(29)

$\begin{split} {\hat l_1} = \,&{\left( {{\boldsymbol{P}}{{\boldsymbol{M}}^{ - {1 / 2}}}{\boldsymbol{z}}} \right)^{\mathrm{H}}}{\boldsymbol{P}}{{\boldsymbol{M}}^{{1 / 2}}}{\hat{\boldsymbol{ M}}^{ - 1}}{{\boldsymbol{M}}^{{1 / 2}}}{{\boldsymbol{P}}^{\mathrm{H}}}\\ & \cdot\left( {{\boldsymbol{P}}{{\boldsymbol{M}}^{ - {1 / 2}}}{\boldsymbol{z}}} \right) - {\hat l_0} = \tau \left( {{{\boldsymbol{n}}^{\mathrm{H}}}{{\bar {\boldsymbol{M}}}^{ - 1}}{\boldsymbol{n}}} \right) - {\hat l_0} \end{split}$

(30)

其中， ${\boldsymbol{n}} = {\boldsymbol{P}}{{\boldsymbol{M}}^{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}{{u}}$ 和 $\bar {\boldsymbol{M}} = {\boldsymbol{P}}{{\boldsymbol{M}}^{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}\hat {\boldsymbol{M}}{{\boldsymbol{M}}^{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}} {{\boldsymbol{P}}^{\mathrm{H}}}$ 。杂波向量 ${\boldsymbol{n}}$ 服从 ${\boldsymbol{n}}{\text{～}}{\mathrm{CN}}\left( {0,{\boldsymbol{I}}} \right)$ 。此外，由于采用CAMLE，矩阵 $\bar {\boldsymbol{M}}$ 与理论散斑协方差矩阵 ${\boldsymbol{M}}$ 之间相互独立^[18]。将式(29)和式(30)代入式(18)和式(26)中，可以发现检测器A-CGGIG和AM-CGGIG的检验统计量均独立于 ${\boldsymbol{M}}$ 和 ${\boldsymbol{p}}$ ，这表明A-CGGIG和AM-CGGIG检测器对 ${\boldsymbol{M}}$ 和 ${\boldsymbol{p}}$ 具有CFAR特性。

4. 失配检测器性能评估

本节在导向矢量匹配和出现失配两种情况下，利用仿真和实测海杂波数据验证提出的A-CGGIG和AM-CGGIG检测器性能及其CFAR特性。理论导向矢量 ${\boldsymbol{p}}$ 和实际导向矢量 ${{\boldsymbol{p}}_{\mathrm{m}}}$ 失配角 $\theta$ 余弦值的平方定义为

${\cos ^2}\theta = \frac{{{{\left| {{{\boldsymbol{p}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{{\boldsymbol{p}}_{\mathrm{m}}}} \right|}^2}}}{{\left( {{{\boldsymbol{p}}^{\mathrm{H}}}{{\boldsymbol{M}}^{ - 1}}{\boldsymbol{p}}} \right)\left( {{\boldsymbol{p}}_{\mathrm{m}}^{\mathrm{H}}{{\boldsymbol{M}}^{ - 1}}{{\boldsymbol{p}}_{\mathrm{m}}}} \right)}}$

(31)

当 ${\cos ^2}\theta = 1$ 时，表示实际导向矢量 ${{\boldsymbol{p}}_{\mathrm{m}}}$ 和理论导向矢量 ${\boldsymbol{p}}$ 相匹配；当 $0 \lt {\cos ^2}\theta \lt 1$ 时，表示理论导向矢量 ${\boldsymbol{p}}$ 失配于实际导向矢量 ${{\boldsymbol{p}}_{\mathrm{m}}}$ 。

4.1 仿真数据实验结果及性能分析

在仿真杂波数据实验中，散斑协方差矩阵 ${\boldsymbol{M}}$ 被建模为1阶滞后衰减系数为 $\rho$ 的指数相关型协方差矩阵，即 ${{\boldsymbol{M}}_{i,j}} = {\rho ^{\left| {i - j} \right|}},1 \le i,j \le N$ ，对于海杂波而言 $\rho \in \left[ {0.9,0.99} \right]$ ，本节设定 $\rho = 0.9$ 。此外，设定脉冲积累数目 $N = 6$ ，参考单元数目 $L = 20$ ，仿真杂波参数为 $a = 1,b = 1,p = 2$ ；目标归一化多普勒频率为 ${f_{\mathrm{d}}} = 0.3$ ，目标检测中的虚警概率为 ${P_{{\mathrm{fa}}}} = {10^{ - 4}}$ ，蒙特卡洛实验次数为10⁵，信杂比(Signal Clutter Ratio, SCR)为

${\mathrm{SCR}} = 10\lg \left( {\frac{{{{\left| \alpha \right|}^2}}}{{{S_\rho }\left( {{f_{\mathrm{d}}}} \right)}}} \right)$

(32)

其中， ${S_\rho }\left( {{f_{\mathrm{d}}}} \right)$ 表示海杂波的多普勒功率谱密度，定义为

${S_\rho }\left( {{f_{\mathrm{d}}}} \right) = 1 + 2\sum\limits_{n = 1}^{N - 1} {\left( {1 - \frac{n}{N}} \right){\rho ^n}} \cos \left( {2\pi {f_{\mathrm{d}}}n} \right)$

(33)

展示了提出的A-CGGIG和AM-CGGIG检测器在导向矢量匹配时，即 ${{\boldsymbol{p}}_{\mathrm{m}}} = {\boldsymbol{p}}$ ，与ANMF, ABORT, GIG-GLRT, MAP-GLRT以及α-AMF检测器的检测性能曲线；当信杂比 ${\mathrm{SCR}} = 6\;{\mathrm{dB}}$ 时，展示了提出的检测器和对比检测器的接收机工作特性(Receiver Operating Characteristic, ROC)曲线。列举了A-CGGIG和AM-CGGIG检测器与对比检测器目标检测概率达到 $90\%$ 时所需要的SCR。

图 2 在匹配情况下提出的检测器与对比检测器的目标检测性能

下载: 全尺寸图片幻灯片

表 1 导向矢量匹配时上述检测器检测概率达到

$90\%$ 时所需要的SCR(dB)

检测器类型	ANMF	ABORT	GIG-GLRT	MAP-GLRT	α-AMF	A-CGGIG	AM-GIGIG
信杂比	8.40	7.61	5.70	5.71	5.82	5.80	5.93

下载: 导出CSV

| 显示表格

综合分析图2和表1，可以发现提出的A-CGGIG和AM-CGGIG检测器在导向矢量匹配时的检测性能与GIG-GLRT和MAP-GLRT检测器的差距小于0.5 dB，且优于α-AMF, ANMF以及ABORT检测器。

在导向矢量出现失配时，所检测到的目标并非是期望方向上的目标，此时希望检测器的性能越差越好。提出的A-CGGIG和AM-CGGIG检测器与对比检测器的抗失配性能对比如图3所示，图3(a)表征检测器在不同SCR和失配角下抗失配性能的台面图，图3中0.9, 0.5, 0.1表示检测概率。从图3中可以发现提出的A-CGGIG和AM-CGGIG的抗失配性能优于GIG-GLRT, MAP-GLRT以及α-AMF检测器。

图 3 在失配情况下提出的检测器与对比检测器的目标检测性能

下载: 全尺寸图片幻灯片

沿着图3(a)纵坐标取点，即可获取检测器在相应失配角下的检测性能曲线。和分别展示了当 ${\cos ^2}\theta = 0.8$ 和 ${\cos ^2}\theta = 0.6$ 时，上述检测器的性能曲线。从图3中可以发现，所有检测器的性能均会随着失配角度的增加而下降。一般而言，检测器的抗失配性能提升是以牺牲检测性能为代价的，而提出的检测器在导向矢量匹配时的检测性能与最优检测器差距小于0.5 dB，且对导向矢量的失配较为敏感，属于同时兼顾目标检测性能和抗失配能力的检测器。

分析了所提A-CGGIG和AM-CGGIG检测器关于目标多普勒频率 ${f_{\mathrm{d}}}$ 和1阶迟滞衰减系数 $\rho$ 的CFAR特性。从和中可以发现，自适应A-CGGIG和AM-CGGIG检测器的 ${P_{{\mathrm{fa}}}}$ 在不同 ${f_{\mathrm{d}}}$ 和 $\rho$ 保持为10^–4不变，与预先设置的 ${P_{{\mathrm{fa}}}}$ 一致。这表明 ${f_{\mathrm{d}}}$ 和 $M$ 不影响自适应A-CGGIG和AM-CGGIG检测器的门限大小，表明提出的检测器对 ${f_{\mathrm{d}}}$ 和 $M$ 具有CFAR特性。

图 4 检测器虚警概率曲线

下载: 全尺寸图片幻灯片

4.2 实测数据实验结果及性能分析

在实测数据实验中，IPIX雷达1998年19980205_171437_ANTSTEP文件VV极化数据被用于验证提出的检测器性能。19980205_171437_ANTSTEP数据共具有28个距离单元，为了方便实验，剔除第6～9受目标回波影响的距离单元，在剩余的纯海杂波数据中添加相干脉冲数目 $N = 6$ 的仿真目标信号，通过蒙特-卡洛实验获得检测概率曲线。展示了CG-GIG分布对实测海杂波数据的拟合结果，可以发现相较于K分布、广义Pareto分布以及CG-IG分布，CG-GIG分布具有较好的拟合效果，其参数估计结果为 $\hat a = 0.15,\hat b = 1.35, \hat p = - 0.7$ 。图5(b)给出了所提A-CGGIG和AM-CGGIG检测器与对比检测器在导向矢量匹配情况时的目标检测性能。

图 5 实测海杂波数据背景下检测器性能分析

下载: 全尺寸图片幻灯片

列举了A-CGGIG和AM-CGGIG检测器与对比检测器目标检测概率达到 $90\%$ 时所需要的SCR。从图5(b)和表2可以发现，A-CGGIG和AM-CGGIG检测器与GIG-GLRT检测器在导向矢量匹配时性能差距小于0.5 dB。

表 2 导向矢量匹配时上述检测器检测概率达到

$90\%$ 时所需要的SCR(dB)

检测器类型	ANMF	ABORT	GIG-GLRT	MAP-GLRT	α-AMF		A-CGGIG	AM-GIGIG
信杂比	12.88	12.16	11.34	11.50	11.43		11.37	11.53

下载: 导出CSV

| 显示表格

图6分析了A-CGGIG和AM-CGGIG检测器与对比检测器在导向矢量失配情况下的检测性能。从图6中可以发现，提出的检测器的抗失配性优于GIG-GLRT和MAP-GLRT检测器。综上所述，提出的检测器仅以牺牲匹配情况下较小的检测性能为代价，提升了出现失配信号时的抗失配性能。

图 6 检测器抗失配性能对比

下载: 全尺寸图片幻灯片

5. 结论

本文针对导向矢量失配情况下的目标检测问题，为了抑制失配信号，在 ${H_0}$ 假设中人为引入虚拟信号 $\beta {\boldsymbol{q}}$ ，并基于GLRT和MAP GLRT准则在GIG纹理背景下发展对散斑协方差矩阵 ${\boldsymbol{M}}$ 和导向矢量 ${\boldsymbol{p}}$ 具有CFAR特性的A-CGGIG和AM-CGGIG检测器。仿真和实测数据实验结果表明，提出的检测器兼顾匹配情况下的目标检测性能和失配情况下的抗失配性能。

图 1 改进方法的算法流程

下载: 全尺寸图片幻灯片

图 2 受挤压的15 m被测同轴电缆

下载: 全尺寸图片幻灯片

图 3 实验测试设置示意图

下载: 全尺寸图片幻灯片

图 4 同轴电缆脉冲冲击响应计算

下载: 全尺寸图片幻灯片

图 5 双指数脉冲信号在受挤压15 m同轴电缆中的传输畸变补偿

下载: 全尺寸图片幻灯片

图 6 改进补偿法对于不同类型信号的畸变补偿

下载: 全尺寸图片幻灯片

图 7 改进补偿法与衰减补偿法的补偿效果对比

下载: 全尺寸图片幻灯片

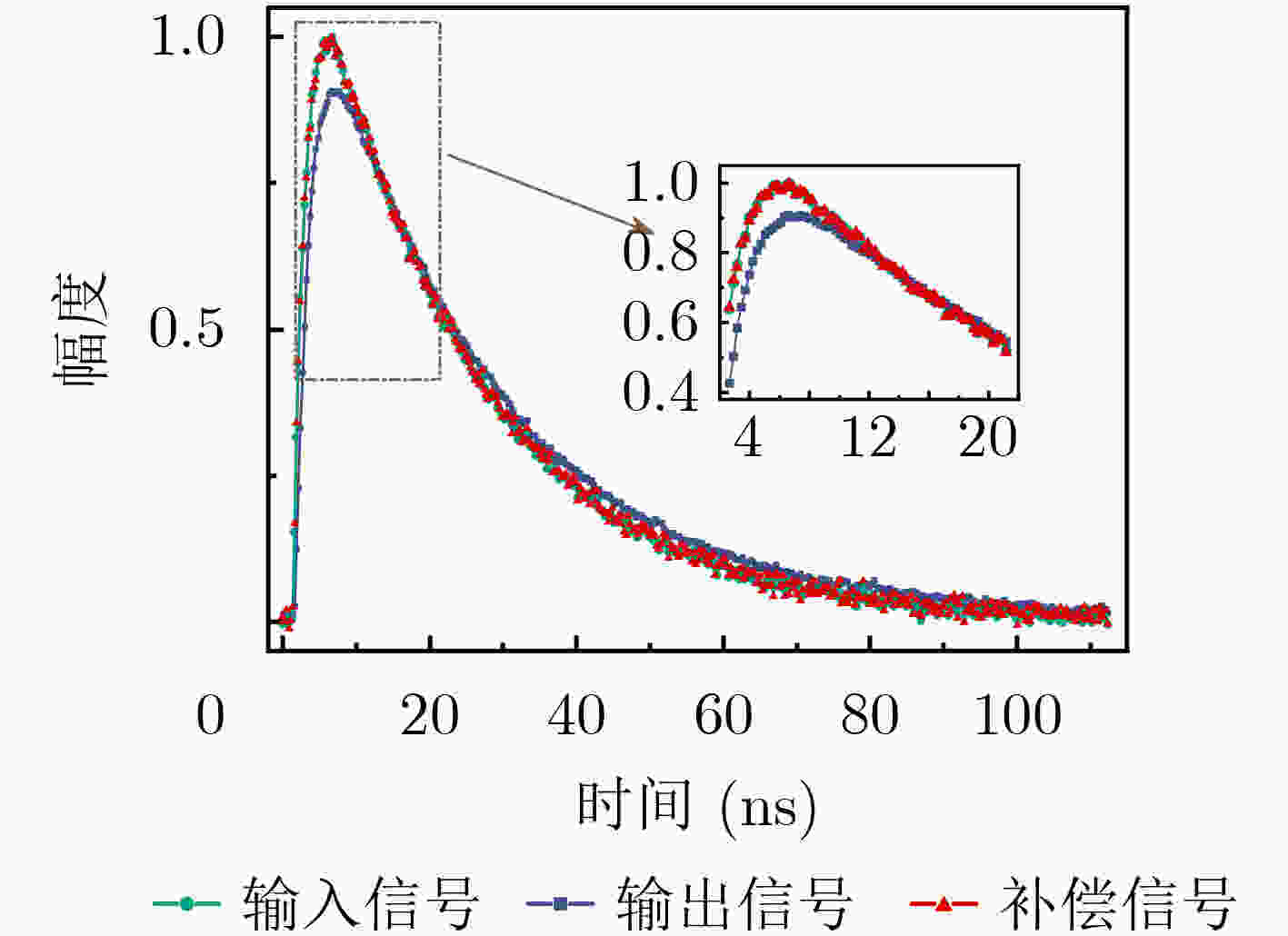
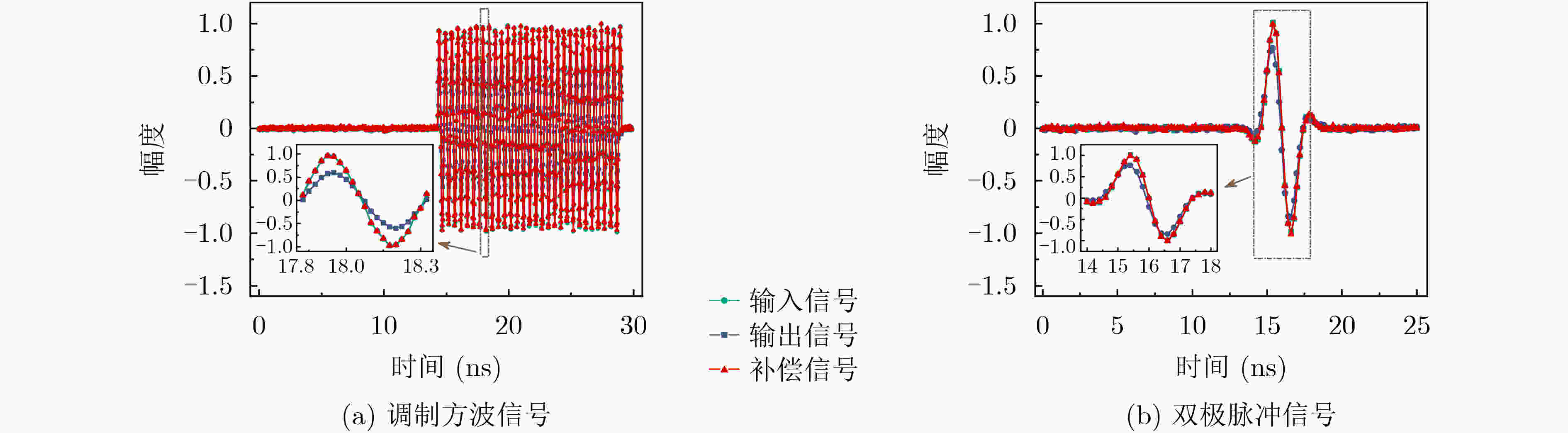
表 1 输出信号、采用改进补偿方法补偿后信号与输入信号间相对偏差(%)

信号样式输出与输入信号偏差补偿与输入信号偏差

双指数脉冲信号 16.5 1.5
调制方波信号 24.4 2.4
双极脉冲信号 25.3 2.3

下载: 导出CSV

表 2 不同补偿方法补偿后信号与输入信号间相对偏差(%)

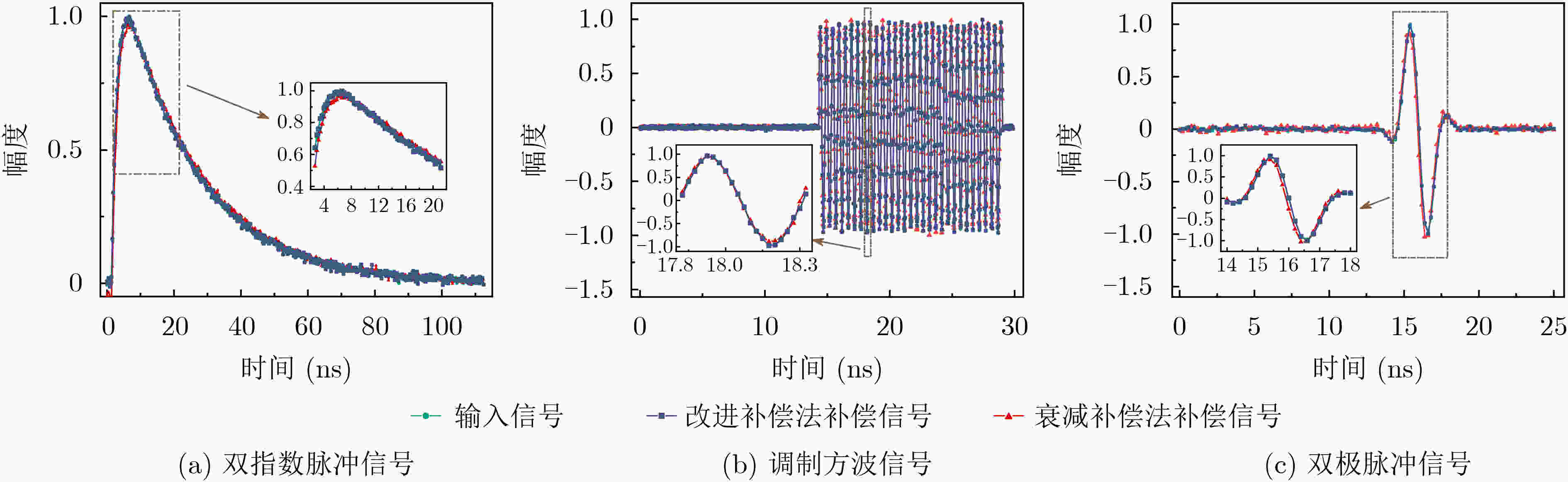
信号样式改进补偿法衰减补偿法

双指数脉冲信号 1.5 9.0
调制方波信号 2.4 10.5
双极脉冲信号 2.3 13.3

下载: 导出CSV

表 3 不同信噪比下改进补偿方法补偿后信号与输入信号间相对偏差(%)

信号样式 45 dB 40 dB 35 dB 30 dB 25 dB 20 dB

双指数脉冲信号 1.5 1.5 1.7 3.4 11.1 17.0
调制方波信号 2.4 2.5 2.8 6.3 19.1 33.1
双极脉冲信号 2.3 2.5 3.0 6.5 18.6 28.3

下载: 导出CSV

表 4 不同信噪比下衰减补偿法补偿后信号与输入信号间相对偏差(%)

信号样式 45 dB 40 dB 35 dB 30 dB 25 dB 20 dB

双指数脉冲信号 9.0 9.3 12.0 17.2 22.0 31.0
调制方波信号 10.5 11.1 15.5 22.5 27.5 35.5
双极脉冲信号 13.3 13.7 16.3 24.3 29.3 36.3

下载: 导出CSV

参考文献(23)

[1]	XIAO Pei, DU Pingan, and ZHANG Bingxue. An analytical method for radiated electromagnetic and shielding effectiveness of braided coaxial cable[J]. IEEE Transactions on Electromagnetic Compatibility, 2019, 61(1): 121–127. doi: 10.1109/TEMC.2018.2814629
[2]	王亚平, 蔡勖. ALICE实验中同轴电缆的信号传输特性的研究[J]. 核电子学与探测技术, 2006, 26(2): 195–198. doi: 10.3969/j.issn.0258-0934.2006.02.019 WANG Yaping and CAI Xu. Study of signal transmission properties of a coaxial cable in ALICE experiment[J]. Nuclear Electronics &Detection Technology, 2006, 26(2): 195–198. doi: 10.3969/j.issn.0258-0934.2006.02.019
[3]	SATO S, YAMAGUCHI T, NISHIMURA S, et al. Influence of measuring cable on lightning impulse parameters[J]. Electronics and Communications in Japan, 2010, 93(6): 1–7. doi: 10.1002/ecj.10288
[4]	戈弋, 黄华, 袁欢. 温度和机械弯曲引起的同轴电缆相位变化特性[J]. 太赫兹科学与电子信息学报, 2019, 17(4): 621–626. doi: 10.11805/TKYDA201904.0621 GE Yi, HUANG Hua, and YUAN Huan. Phase characteristics of coaxial cable caused by temperature and mechanical bending[J]. Journal of Terahertz Science and Electronic Information Technology, 2019, 17(4): 621–626. doi: 10.11805/TKYDA201904.0621
[5]	贾文超, 董冰, 李林. 同轴电缆形变TDR监测技术的研究与实现[J]. 计算机测量与控制, 2007, 15(10): 1276–1278. doi: 10.3969/j.issn.1671-4598.2007.10.004 JIA Wenchao, DONG Bing, and LI Lin. Research and realization of coaxial-cable deformation TDR monitoring technology[J]. Computer Measurement &Control, 2007, 15(10): 1276–1278. doi: 10.3969/j.issn.1671-4598.2007.10.004
[6]	陈云敏, 梁志刚, 陈仁朋, 等. 有缺陷同轴电缆的时域反射特性及应用[J]. 浙江大学学报: 工学版, 2005, 39(1): 51–56, 64. CHEN Yunmin, LIANG Zhigang, CHEN Renpeng, et al. Time domain reflectometry property of defective coaxial cable and its applications[J]. Journal of Zhejiang University:Engineering Science, 2005, 39(1): 51–56, 64.
[7]	CHOO J, CHOO J, and KIM Y H. Evaluation of electromagnetic interference from axially ruptured coaxial cable with multiple dielectrics used in nuclear power plants[J]. IEEE Transactions on Electromagnetic Compatibility, 2019, 61(3): 860–869. doi: 10.1109/TEMC.2018.2835665
[8]	渠红光, 李宪优, 田耕, 等. 基于衰减特性的电缆传输畸变软件补偿[J]. 装备指挥技术学院学报, 2010, 21(2): 87–90. QU Hongguang, LI Xianyou, TIAN Geng, et al. Attenuation compensation by software based on the character of transfers of the cable[J]. Journal of the Academy of Equipment Command &Technology, 2010, 21(2): 87–90.
[9]	付佳斌, 卿燕玲, 卫兵, 等. 同轴电缆测量纳秒脉冲信号衰减的数字补偿[J]. 强激光与粒子束, 2011, 23(10): 2826–2830. doi: 10.3788/HPLPB20112310.2826 FU Jiabin, QING Yanlin, WEI Bing, et al. Numerical compensation for coaxial cable signal degradation[J]. High Power Laser and Particle Beams, 2011, 23(10): 2826–2830. doi: 10.3788/HPLPB20112310.2826
[10]	黄豹. 新的高频同轴电缆补偿原理[J]. 核电子学与探测技术, 1985, 5(4): 193–198. HUANG Bao. New principle of high frequency coaxial cable equalization[J]. Nuclear Electronics &Detection Technology, 1985, 5(4): 193–198.
[11]	WHALLEY W B. Color-television coaxial cable termination and equalization[J]. SMPTE Journal 1955, 1995, 64(1): 8–12.
[12]	SARKAR T K, TSENG F I, RAO S M, et al. Deconvolution of impulse response from time-limited input and output: Theory and experiment[J]. IEEE Transactions on Instrumentation and Measurement, 1985, IM-34(4): 541–546. doi: 10.1109/TIM.1985.4315400
[13]	王园, 朱江淼. 应用反卷积实现脉冲计量中的信号重构与系统辨识[J]. 信号处理, 2013, 29(4): 532–535. doi: 10.3969/j.issn.1003-0530.2013.04.017 WANG Yuan and ZHU Jiangmiao. Signal reconstruction and system identification using the deconvolution in pulse metrology[J]. Signal Processing, 2013, 29(4): 532–535. doi: 10.3969/j.issn.1003-0530.2013.04.017
[14]	THOMPSON A M and KAY J. On some Bayesian choices of regularization parameter in image restoration[J]. Inverse Problems, 1993, 9(6): 749–761. doi: 10.1088/0266-5611/9/6/011
[15]	YAN Gang and SUN Hao. A non-negative Bayesian learning method for impact force reconstruction[J]. Journal of Sound and Vibration, 2019, 457: 354–367. doi: 10.1016/j.jsv.2019.06.013
[16]	骆睿, 刘莉, 佟瑞, 等. 基于Tikhonov正则化的高分辨率群时延测量与计算方法[J]. 电子学报, 2019, 47(5): 1044–1048. doi: 10.3969/j.issn.0372-2112.2019.05.010 LUO Rui, LIU Li, TONG Rui, et al. High-resolution group delay measurement and calculation method based on Tikhonov regularization[J]. Acta Electronica Sinica, 2019, 47(5): 1044–1048. doi: 10.3969/j.issn.0372-2112.2019.05.010
[17]	韩玉兵, 吴乐南, 张冬青. 基于正则化处理的超分辨率重建[J]. 电子与信息学报, 2007, 29(7): 1713–1716. HAN Yubing, WU Lenan, and ZHANG Dongqing. Super-resolution reconstruction based on regularization[J]. Journal of Electronics &Information Technology, 2007, 29(7): 1713–1716.
[18]	王鹏宇, 宋千, 周智敏. 基于多测量动态聚类的压缩感知增强成像方法[J]. 电子与信息学报, 2013, 35(11): 2664–2671. WANG Pengyu, SONG Qian, and ZHOU Zhimin. Enhanced compressive imaging approach based on multi-measurement and dynamic clustering[J]. Journal of Electronics &Information Technology, 2013, 35(11): 2664–2671.
[19]	JOHNSTON P R and GULRAJANI R M. Selecting the corner in the L-curve approach to Tikhonov regularization[J]. IEEE Transactions on Biomedical Engineering, 2000, 47(9): 1293–1296. doi: 10.1109/10.867966
[20]	王师萍. 带非负限制的增广Tikhonov正则化方法[D]. [硕士论文], 上海交通大学, 2010. WANG Shiping. Augmented Tikhonov regularization with nonnegative constraints[D]. [Master dissertation], Shanghai Jiao Tong University, 2010.
[21]	WANG Jingbo and ZABARAS N. Hierarchical Bayesian models for inverse problems in heat conduction[J]. Inverse Problems, 2005, 21(1): 183–206. doi: 10.1088/0266-5611/21/1/012
[22]	JIN Bangti and ZOU Jun. A Bayesian inference approach to the ill-posed Cauchy problem of steady-state heat conduction[J]. International Journal for Numerical Methods in Engineering, 2008, 76(4): 521–544. doi: 10.1002/nme.2350
[23]	JIN Bangti and ZOU Jun. Augmented Tikhonov regularization[J]. Inverse Problems, 2009, 25(2): 025001. doi: 10.1088/0266-5611/25/2/025001

施引文献

资源附件(0)

访问统计

图(7) / 表(4)

计量

文章访问数: 1026
HTML全文浏览量: 366
PDF下载量: 49
被引次数: 0

1. 引言
2. 失配信号的目标检测模型
3. 基于GIG纹理结构的失配检测器
3.1 GLRT准则下的失配检测器
3.2 MAP GLRT准则下的失配检测器
3.3 失配检测器的CFAR特性分析
4. 失配检测器性能评估
4.1 仿真数据实验结果及性能分析
4.2 实测数据实验结果及性能分析
5. 结论

1. 引言
2. 失配信号的目标检测模型
3. 基于GIG纹理结构的失配检测器
3.1 GLRT准则下的失配检测器
3.2 MAP GLRT准则下的失配检测器
3.3 失配检测器的CFAR特性分析
4. 失配检测器性能评估
4.1 仿真数据实验结果及性能分析
4.2 实测数据实验结果及性能分析
5. 结论

参考文献(23)

施引文献

资源附件(0)

访问统计

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

基于改进贝叶斯非负Tikhonov正则化方法的同轴电缆信号传输畸变补偿研究

doi: 10.11999/JEIT210068

作者简介:
秦风：男，1985年生，副研究员，研究方向为电磁脉冲环境测试、电磁环境效应及防护

高原：男，1989年生，助理研究员，研究方向为电磁脉冲环境仿真与测试

吴双：男，1993年生，初级工，研究方向为电磁环境测试

通讯作者:
高原　18142550916@163.com

计量

Signal Compensation of Coaxial Cable Based on Modified Non-negative Tikhonov Regularization Method within Bayesian Inference

1. 引言

2. 失配信号的目标检测模型

3. 基于GIG纹理结构的失配检测器

3.1 GLRT准则下的失配检测器

3.2 MAP GLRT准则下的失配检测器

3.3 失配检测器的CFAR特性分析

4. 失配检测器性能评估

4.1 仿真数据实验结果及性能分析

4.2 实测数据实验结果及性能分析

5. 结论

计量

目录

1. 引言

2. 失配信号的目标检测模型

3. 基于GIG纹理结构的失配检测器

3.1 GLRT准则下的失配检测器

3.2 MAP GLRT准则下的失配检测器

3.3 失配检测器的CFAR特性分析

4. 失配检测器性能评估

4.1 仿真数据实验结果及性能分析

4.2 实测数据实验结果及性能分析

5. 结论

信号样式	输出与输入信号偏差	补偿与输入信号偏差
双指数脉冲信号	16.5	1.5
调制方波信号	24.4	2.4
双极脉冲信号	25.3	2.3

信号样式	改进补偿法	衰减补偿法
双指数脉冲信号	1.5	9.0
调制方波信号	2.4	10.5
双极脉冲信号	2.3	13.3

信号样式	45 dB	40 dB	35 dB	30 dB	25 dB	20 dB
双指数脉冲信号	1.5	1.5	1.7	3.4	11.1	17.0
调制方波信号	2.4	2.5	2.8	6.3	19.1	33.1
双极脉冲信号	2.3	2.5	3.0	6.5	18.6	28.3

留言板

基于改进贝叶斯非负Tikhonov正则化方法的同轴电缆信号传输畸变补偿研究

doi: 10.11999/JEIT210068

作者简介: 秦风：男，1985年生，副研究员，研究方向为电磁脉冲环境测试、电磁环境效应及防护 高原：男，1989年生，助理研究员，研究方向为电磁脉冲环境仿真与测试 吴双：男，1993年生，初级工，研究方向为电磁环境测试

通讯作者: 高原 18142550916@163.com

计量

出版历程

Signal Compensation of Coaxial Cable Based on Modified Non-negative Tikhonov Regularization Method within Bayesian Inference

1. 引言

2. 失配信号的目标检测模型

3. 基于GIG纹理结构的失配检测器

3.1 GLRT准则下的失配检测器

3.2 MAP GLRT准则下的失配检测器

3.3 失配检测器的CFAR特性分析

4. 失配检测器性能评估

4.1 仿真数据实验结果及性能分析

4.2 实测数据实验结果及性能分析

5. 结论

计量

出版历程

目录

1. 引言

2. 失配信号的目标检测模型

3. 基于GIG纹理结构的失配检测器

3.1 GLRT准则下的失配检测器

3.2 MAP GLRT准则下的失配检测器

3.3 失配检测器的CFAR特性分析

4. 失配检测器性能评估

4.1 仿真数据实验结果及性能分析

4.2 实测数据实验结果及性能分析

5. 结论

作者简介:
秦风：男，1985年生，副研究员，研究方向为电磁脉冲环境测试、电磁环境效应及防护

高原：男，1989年生，助理研究员，研究方向为电磁脉冲环境仿真与测试

吴双：男，1993年生，初级工，研究方向为电磁环境测试

通讯作者:
高原　18142550916@163.com