基于稀疏步进调频信号的低信噪比逆合成孔径雷达成像

王樾; 白雪茹; 周峰

doi:10.11999/JEIT210056

基于稀疏步进调频信号的低信噪比逆合成孔径雷达成像

doi: 10.11999/JEIT210056

王樾¹,
白雪茹²,
周峰^1, ,

1.
西安电子科技大学电子信息攻防对抗与仿真技术教育部重点实验室西安 710071
2.
西安电子科技大学雷达信号处理国家重点实验室西安 710071

基金项目: 国家自然科学基金(61971332, 61631019)

详细信息

作者简介:
王樾：男，1995年生，硕士，研究方向为ISAR成像

白雪茹：女，1984年生，教授，研究方向为高分辨雷达成像、雷达目标识别

周峰：男，1980年生，教授，研究方向为电子对抗、雷达成像

通讯作者:
周峰　fzhou@mail.xidian.edu.cn

中图分类号: TN957
计量
- 文章访问数: 1251
- HTML全文浏览量: 463
- PDF下载量: 131
- 被引次数: 20
出版历程
- 收稿日期: 2021-01-18
- 修回日期: 2021-03-31
- 网络出版日期: 2021-04-19
- 刊出日期: 2022-03-28

High-resolution Inverse Synthetic Aperture Radar Imaging with Sparse Stepped-frequency Chirp Signals under Low Signal to Noise Ratio

WANG Yue¹,
BAI Xueru²,
ZHOU Feng^{1
, ,}

1.
Key Laboratory of Electronic Information Countermeasure and Simulation Technology, Ministry of Education, Xidian University, Xi’an 710071, China
2.
National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China

Funds: The National Natural Science Foundation of China (61971332, 61631019)

摘要

摘要: 针对稀疏步进调频信号对目标径向运动敏感且低信噪比(SNR)下难以聚焦成像的问题，该文提出基于遗传算法和稀疏贝叶斯学习的平动补偿与高分辨逆合成孔径雷达(ISAR)成像方法。首先，针对稀疏步进调频信号建立回波模型和稀疏观测模型，通过构造参数化字典，将ISAR成像问题转换为目标运动参数估计与高分辨距离像(HRRP)合成的联合问题。然后，对目标高分辨距离像引入Gamma-Gauss先验，并采用变分贝叶斯推断(VBI)对散射点进行估计。在此基础上，通过遗传算法迭代同步获得目标运动参数与高质量HRRP，最终实现高分辨聚焦成像和运动参数精确估计。不同场景下的仿真和实测数据处理结果验证了所提算法的有效性。
- 逆合成孔径雷达(ISAR) /
- 运动参数估计 /
- 稀疏贝叶斯学习 /
- 遗传算法
Abstract: To solve the sensitivity of sparse stepped-frequency chirp signals to target radial motion and to achieve high-resolution imaging with low Signal to Noise Ratio (SNR), a translation compensation and high-resolution Inverse Synthetic Aperture Radar (ISAR) imaging based on genetic algorithm and sparse Bayesian learning is proposed. Firstly, an echo model and a sparse observation model are established for the sparse stepped-frequency chirp signal. A parameterized dictionary is then constructed to turn ISAR imaging to the joint estimation of target motion parameter and High-Resolution Range Profile (HRRP) synthesis. Secondly, the Gamma-Gaussian prior is introduced to the high-resolution range profile of the target, and the scattering center is estimated by the Variational Bayesian Inference (VBI) algorithm. On this basis, target motion parameters and high-quality HRRP are obtained through the iteration of genetic algorithm. Hence, high-resolution imaging of the moving targets is achieved while the motion parameters are accurately estimated. The effectiveness of the proposed method is verified by simulation and real data processing result in various scenes.
- Inverse Synthetic Aperture Radar (ISAR) /
- Motion parameter estimation /
- Sparse Bayesian learning /
- Genetic algorithm

HTML全文

1. 引言

萤火虫算法(Firefly Algorithm, FA)是一种模拟萤火虫吸引行为的群智能优化算法^[1]。它在特征提取、聚类等问题上的性能胜过遗传算法、粒子群算法等^[2–5]。因此，FA被应用于解决网络、图像处理等越来越多的工程和科学领域的重要优化问题^[5]。随着应用范围的扩大，人们对算法性能的期望也变得更高。

为了提高算法性能，学者们对FA进行了许多改进。这些改进首先是参数控制，如Yu等人^[6]提出了一种步长动态调整策略。Haji等人^[3]则探讨了步长、吸引力等多个参数的最优取值组合。Wang等人^[7]对步长和吸引力进行了理论性分析，并结合参数自身特性提出自适应调整策略。参数控制有助于提高算法性能，但面临复杂优化问题时对算法性能的提升非常有限。一些学者开始研究不同的吸引模型。Wang等人^[8]提出了随机吸引模型，从群体中随机选择一只萤火虫。Verma等人^[9]提出基于维度构造一只全局最优的虚拟萤火虫。Zhang等人^[4]则根据最大回报成本比选择一只萤火虫。萤火虫受选出的萤火虫吸引而移动。这些吸引模型降低了算法时间复杂度，但需结合其它技术才能提高算法的收敛精度。另一类改进是与其它技术混合，如Gandomi等人^[10]将混沌技术引入FA，提高了算法的全局搜索能力。Hassanzadeh等人^[2]结合模糊逻辑，让当前萤火虫受模糊集合中萤火虫的吸引，从而增强优质萤火虫对其它个体的吸引作用。这类改进结合不同技术的优点，能够取得较好的效果，本文的研究属于这一类。

近年来，国内外不少学者将反向学习(Opposition-Based Learning, OBL)^[11]与群智能算法结合，如差分演化算法、粒子群优化算法等。这些方法对算法性能的提升表现出显著效果^[12,13]。目前OBL与FA的结合也有些研究成果，其中比较有代表性的工作有，Verma等人^[9]在FA的种群初始化时用OBL获得更好的初始种群。Yu等人^[14]则利用OBL计算迭代最差萤火虫的反向解。这些方法利用了反向个体提供的丰富信息，提高了算法收敛精度。但他们在计算反向个体时，将个体的所有维都取其反向值。Park等人^[15]指出，对于一个个体，并不是所有维上的反向值都优于个体的值。他们在应用OBL到差分演化算法时提出将个体与反向个体进行二项式交叉，得到两个部分维是反向值的候选解，从而保存个体和反向个体中的部分信息，进一步增强了算法的搜索能力。然而，上述方法虽能够保存个体和反向个体中的部分信息，但不能获得两者中有用信息的最优组合。因此，进一步提升算法性能的关键在于如何发现和保存个体和反向个体中有用信息的组合。

为了发现并充分利用个体和反向个体中隐藏的有用信息，本文结合正交试验设计和反向学习技术，设计一种正交反向学习策略(Orthogonal Opposition-Based Learning, OOBL)，利用正交试验设计产生一组部分维上取反向值的候选解，从而挖掘并保存个体和反向个体中的有用信息；再将OOBL应用到FA算法，提出一种基于正交反向学习策略的萤火虫算法(Orthogonal Opposition-based Firefly Algorithm, OOFA)。

2. 萤火虫算法与反向学习

2.1 萤火虫算法FA

FA中，每只萤火虫代表一个可行解，被随机分布在目标函数的搜索空间内。对于一个D维搜索空间，设种群个数为N，第i只萤火虫的位置表示为 ${X_i} = ({x_{i1}},{x_{i2}},·\!·\!·,{x_{iD}})$ ，则其位置更新方程的定义为^[1]

$x_i^{t + 1} = x_i^t + {\beta _0}{{\rm e}^{ - \gamma {r_{ij}}\!\!^2}}(x_j^t - x_i^t) + {\alpha ^t}{\varepsilon ^t}$

(1)

式(1)中， $x_i^{t + 1}$ 表示萤火虫i在 $t + 1$ 时刻的位置。等号右侧第2项表示萤火虫i因受到萤火虫j的吸引而产生的位移，其中， ${\beta _0}$ 表示光源(距离r=0)处的吸引力，通常取1; ${r_{ij}}$ 表示两只萤火虫i, j之间的距离，计算公式见式(2); $\gamma$ 表示媒介对光的吸收率，通常取１。

${r_{ij}} = {\left\| {{x_i} - {x_j}} \right\|_2} = \sqrt {\sum\limits_{k = 1}^d {{{({x_{ik}} - {x_{jk}})}^2}} }$

(2)

式(1)等号右侧的第3项是随机项，其中， ${\varepsilon^t}$ 是t时刻服从均匀分布的随机因子， ${\alpha ^t} \in [0,1]$ 表示t时刻的步长。为了更好地平衡算法的探索与开发能力，Yang^[16]提出迭代递减的 $\alpha$ ，计算公式见式(3)。

${\alpha ^t} = {\alpha ^{t - 1}}\delta , \ 0 < \delta < 1$

(3)

其中， $\delta$ 是一个冷却系数。

2.2 反向学习

OBL是Tizhoosh^[11]提出的一种智能技术，其思想是同时评估当前点和其反向点，择优使用，以此来加速搜索进程。OBL的基本定义见定义1。

定义1 若x是定义在实数集R上[a, b]区间的一个实数，即x $\; \in\;$ [a, b]，则x的反向点定义如式(4)^[11]：

$\overset{{{\smile}}}{x} = a + b - x$

(4)

在OBL的基础上，Rahnamayan等人^[17]为了充分利用群体搜索信息，提出重心反向(Centroid Opposition, CO)，以群体重心为参考点计算反向点。重心与基于重心的反向点定义如下：

定义2 设 $({X_1},{X_2},·\!·\!· {X_N})$ 是D维搜索空间中带有单位质量的N个点，则整体的重心定义为

${G_j} = \frac{1}{N}{\sum\limits_{i = 1}^N {{x_{ij}}} }, \ j = 1, 2,·\!·\!·, D$

(5)

定义3 若一个离散均匀的整体的重心为G，则该整体中某一点X_i的反向点定义为

${\overset{{{\smile}}}{X} _i} = 2 \times G - {X_i}, \ i = 1,2,·\!·\!·, n$

(6)

反向点位于一个具有动态边界的搜索空间[a_j, b_j]中，动态边界按式(7)计算。当反向点超出边界时，按式(8)重新计算反向点，其中 ${\rm{rand}}(0,1)$ 是[0, 1]上的一个随机数。

${a_j} = \min ({X_j}), {b_j} = {\rm max}({X_j})\quad\quad\quad\quad\quad\quad$

(7)

${\overset{{{\smile}}}{x}_i}_j = \left\{ {\begin{aligned} & {{a_j} + {\rm{rand}}(0,1) \times ({G_j} - {a_j}), \ {x} }_{ij} < {{a_j}} \\ & {{G_j} + {\rm{rand}}(0,1) \times ({b_j} - {G_j}), \ {x} }_{ij} > {{b_j}} \end{aligned}} \right.$

(8)

3. 正交反向学习萤火虫算法OOFA

3.1 正交反向学习策略

正交试验设计是通过使用正交表以较少的试验次数发现各因素的不同水平之间的最优组合^[18]。例如，对于2水平7因素的试验，若测试所有组合，则需 ${2^7} = 128$ 次试验。但用正交试验设计，采用正交表 ${L_8}({2^7})$ ，见式(9)，则仅需８次试验就可以找出最优组合，大幅减少了试验次数。

${L_8}({2^7}) = \left[ {\begin{array}{*{20}{c}} 1&1&1&1&1&1&1 \\ 1&1&1&2&2&2&2 \\ 1&2&2&1&1&2&2 \\ 1&2&2&2&2&1&1 \\ 2&1&2&1&2&1&2 \\ 2&1&2&2&1&2&1 \\ 2&2&1&1&2&2&1 \\ 2&2&1&2&1&1&2 \end{array}} \right]$

(9)

OOBL策略中，问题的维度对应正交试验设计中的因素，个体和反向个体在各维度上的值作为各因素的水平，这样就可以进行一个2水平D因素的正交试验。构建试验解时，当正交表的元素为1，试验解对应维上取个体的值；当正交表的元素为2，试验解对应维上取反向个体的值。为了直观地说明OOBL中试验解的构建，以一个7维问题为例，给出了用 ${L_8}({2^7})$ 构建的试验解，见图1。OOBL的具体步骤见算法1(表1)。

表 1 算法1：OOBL策略

输入：种群X，一个个体的索引ind和正交表L；
输出：新种群X。
步骤：
(1) 根据式(5)计算当前种群重心G；
(2) 根据式(6)计算指定个体的反向个体ox；
(3) 根据式(7)更新群体边界；根据式(8)对ox进行边界检查；
(4) for i=1: L的行数M
(5) 　for j=1: 问题维数D
(6)　　 if L(i, j)==1
(7)　　　oox(i, j)=X(ind, j)；
(8) 　　else
(9)　　　 oox(i, j)=ox( j)；
(10)　　end if
(11)　end for
(12) end for
(13) 评估正交反向候选解，评估次数FEs=FEs+M–1；
(14) 从X和正交反向候选解中选出适应值最优的N个个体。

下载: 导出CSV

| 显示表格

图 1 试验解的构建

下载: 全尺寸图片幻灯片

OOBL的关键步骤在于试验解的构建，即第4步到第12步。一个个体通过正交试验将得到M个试验解。M也是正交表的行数，计算公式见式(10)。

$M = {2^{\left\lceil {{{\log }_2}(D + 1)} \right\rceil }}$

(10)

根据正交表的特性，第1个试验解与该个体相同，不需要评估。另外的 $M - 1$ 个试验解的部分维上是个体的值，部分维上取反向个体的值，这部分试验解称为正交反向候选解。它们是个体和反向个体不同维上信息的代表性的组合，需要评估。因此执行一次OOBL策略需要的函数评估次数是 $M - 1$ 次。从种群和正交反向候选解中选择最优的N个个体作为新种群，这样可以充分发掘个体和反向个体中有用信息的组合，并更多地在种群中保存这些信息。

3.2 OOFA算法

本节把提出的正交重心反向学习策略OOBL结合到FA中，提出一种正交反向学习的FA算法，简称为OOFA，见算法2(表2)。

表 2 算法2：OOFA算法

输入：目标函数；
输出：全局最优位置及适应值。
步骤：
(1) 随机初始化有N个个体的种群X；
(2) 评估初始种群f(X)，当前函数评估次数FEs=N；
(3) 根据种群适应值排序；
(4) 根据函数维数D，生成2水平D因素的正交表L；
(5) while 未达迭代终止条件
(6)　　 for i=1:N
(7)　　　 for j=1: i
(8) 　　　　根据式(1)和式(2)，第i个个体向第j个个体移位；
(9) 　　　end for
(10) 　end for
(11) 　对种群进行边界检查；
(12) 　评估种群，函数评估次数FEs=FEs+N；
(13) 　随机选择群体中一个个体，执行OOBL；
(14)　根据式(3)更新步长因子；
(15) end while

下载: 导出CSV

| 显示表格

OOFA算法中，生成2水平D因素的正交表的算法见文献[19]的附录部分。OOFA保持了FA算法的基本框架和主要操作，仅在种群移位之后增加了随机选择一个个体并对它执行OOBL操作。设目标函数的维度为D，种群规模为N，最大迭代次数为T。OOFA算法的主要操作是第6步至第10步的萤火虫移位操作和第13步的OOBL，前者时间复杂度都是 $O({N^2}D)$ ，后者时间复杂度是 $O({D^2})$ 。这两种操作都在迭代过程中，所以总的时间复杂度为 $O(T{N^2}D) + O(T{D^2})$ ，略去低阶项，算法总时间复杂度为 $O(T{N^2}D)$ 。OOFA与FA算法时间复杂度一致，对算法的改进没有增加过多的计算开销。

迭代初期，OOFA通过执行反向计算引入了不同个体在不同维上的反向搜索空间，从而拓展了潜在的有希望的搜索空间，加强了全局搜索能力。随着迭代不断进行，反向搜索空间不断减小，此时OOFA通过正交试验设计对个体周围较小的空间和反向空间进行局部探索，从而提升了算法的局部勘探能力。

4. 仿真实验与结果分析

4.1 测试函数

为了全面客观地对OOFA算法的性能做出评价，选择CEC 2013测试集。该测试集一共28个函数，包含了单峰、多峰和组合函数，比传统测试集的函数更多更复杂，可以更好地代表广泛的实际优化问题，具体定义见文献[20]。实验运行在一台配置为：Intel Core(TM)2 Duo CPU E4600 @ 2.40 GHz；内存2 GB；操作系统为Windows 8 专业版的计算机上。所有算法在Matlab 2012下进行仿真。实验中，最大函数评估次数设为10⁵，种群规模N=30，问题维数D=30，每个算法在每个函数上独立运行25次。

4.2 OOBL策略有效性分析

为了验证OOBL策略的有效性，对OOFA与FA在收敛精度、稳定性、收敛速度和运行时间上进行比较。为了公平比较，根据Yang^[16]给出的参数取值范围，两种算法的参数均设为： ${\beta _0} = 1,$ ${\alpha _0} = 0.5$ , $\gamma = 1$ , $\delta = 0.97$ 。比较收敛精度和稳定性时，迭代终止条件设为到达最大函数评估次数，记录算法找到的最优解与函数最优值之差的均值(Mean)和标准差(SD)。比较收敛速度和运行时间时，迭代终止条件设为到达给定精度或到达最大函数评估次数，记录算法的平均函数评估次数(FEs)和平均运行时间(T)。时间单位为s。因OOFA的收敛精度高于FA，所以给定精度以FA在各函数上能达到的平均精度为基准进行设定。为了进一步分析两者收敛速度的差异，求各函数上FA与OOFA的平均函数评估次数之比，即加速比(R)。实验结果见表3。

表 3 FA与OOFA的比较结果

函数	FA				OOFA				加速比R
函数	Mean	SD	FEs	T (s)	Mean	SD	FEs	T (s)	加速比R
f₁	5.16E+04	6.35E+03	80232	3.85	1.70E–10	8.44E–10	1091	0.03	73.54
f₂	7.30E+08	2.15E+08	72314	3.82	3.39E+07	1.04E+07	1704	0.06	42.44
f₃	4.74E+16	1.43E+17	16662	0.94	1.61E+09	8.63E+08	616	0.02	27.05
f₄	9.36E+04	1.29E+04	37973	1.94	7.25E+04	1.22E+04	5669	0.17	6.70
f₅	1.58E+04	3.90E+03	44544	2.25	1.06E+02	3.32E+01	1421	0.04	31.35
f₆	8.71E+03	2.01E+03	36463	1.85	6.90E+01	2.47E+01	904	0.03	40.34
f₇	1.08E+05	1.13E+05	32322	2.11	4.11E+01	1.12E+01	1082	0.05	29.87
f₈	2.10E+01	5.29E–02	82741	4.87	2.10E+01	6.09E–02	85977	3.23	0.96
f₉	4.28E+01	1.42E+00	64643	18.07	2.14E+01	4.18E+00	4178	1.08	15.47
f₁₀	6.79E+03	1.12E+03	72373	3.95	1.67E+01	1.19E+01	1094	0.04	66.15
f₁₁	8.38E+02	9.77E+01	52407	2.85	1.13E+01	3.35E+00	989	0.03	52.99
f₁₂	8.43E+02	9.43E+01	56517	3.51	1.05E+02	3.38E+01	1133	0.05	49.88
f₁₃	8.17E+02	9.91E+01	60595	3.89	8.64E+01	3.04E+01	1304	0.06	46.47
f₁₄	8.10E+03	3.23E+02	80418	4.48	1.55E+03	5.45E+02	5359	0.19	15.01
f₁₅	8.07E+03	3.59E+02	72859	4.24	4.41E+03	7.63E+02	5598	0.21	13.02
f₁₆	3.19E+00	5.04E–01	57793	11.01	1.79E+00	5.38E–01	10998	1.86	5.25
f₁₇	1.40E+03	1.91E+02	56622	2.95	4.09E+01	3.16E+00	1955	0.06	28.96
f₁₈	1.44E+03	1.68E+02	52612	3.01	1.06E+02	2.98E+01	1484	0.05	35.45
f₁₉	1.04E+06	4.38E+05	52422	2.75	3.34E+00	7.17E–01	1230	0.04	42.62
f₂₀	1.50E+01	1.43E–05	8888	0.51	1.50E+01	3.14E–05	962	0.04	9.24
f₂₁	3.57E+03	1.80E+02	64395	5.24	2.92E+02	2.75E+01	1901	0.12	33.87
f₂₂	8.87E+03	3.07E+02	61069	4.75	1.91E+03	1.25E+03	4629	0.27	13.19
f₂₃	9.05E+03	4.02E+02	49134	4.21	5.61E+03	1.21E+03	4437	0.29	11.07
f₂₄	4.15E+02	2.78E+01	32295	10.01	2.17E+02	6.37E+00	652	0.19	49.53
f₂₅	4.09E+02	1.66E+01	44404	13.74	2.70E+02	1.38E+01	728	0.21	60.99
f₂₆	3.08E+02	4.83E+01	64359	20.94	2.95E+02	2.03E+01	41667	12.63	1.54
f₂₇	1.64E+03	5.93E+01	32762	10.50	4.51E+02	6.27E+01	955	0.29	34.31
f₂₈	6.25E+03	5.82E+02	48551	4.94	3.00E+02	6.06E–03	1499	0.12	32.39

下载: 导出CSV

| 显示表格

分析表3可知，OOFA仅在函数 ${f_8}$ 和 ${f_{20}}$ 上与FA取得相同结果，在其它26个函数上所得结果的精度均优于FA，且在 ${f_1},{f_3}$ 和 ${f_{19}}$ 等多个函数上的精度高于FA多个数量级，这说明OOBL有助于提高算法收敛精度。从标准差上看，函数 ${f_8},{f_9},{f_{14}},{f_{15}},$ ${f_{16}},{f_{20}},{f_{22}},{f_{23}}$ 和 ${f_{27}}$ 上，FA的结果略优于OOFA，但其它19个函数上，OOFA的结果均优于FA，这说明OOBL策略使算法的稳定性更好。总之，OOBL策略虽花费了一定的函数评估次数，但获得了更大的收益，它聚合了个体与反向个体中的有用信息，加快了算法的搜索进程，有效提高了算法的收敛精度，在函数评估次数相同的情况下，OOFA的收敛精度明显高于FA。

从平均迭代次数上来看，到达相同精度，OOFA在除了 ${f_8}$ 之外的其它27个函数上需要的函数评估次数均少于FA。OOFA平均运行时间也少于FA，其主要原因是到达给定精度时OOFA需要的函数评估次数比FA所需要的更少些。 ${f_8}$ 上OOFA虽然平均函数评估次数略多于FA，但平均运行时间仍然少于FA。由3.2节OOFA算法时间复杂度的分析可知，萤火虫移位操作的时间复杂度高于OOBL的时间复杂度，而FA中萤火虫移位操作的执行次数多于OOFA中移位操作的执行次数。所以， ${f_8}$ 上OOFA使用与FA相近次数的函数评估，但运行时间仍少些。从加速比上可看出，除 ${f_8}$ 之外的其它27个函数上加速比均大于1，最大加速比到达73.57。可见，OOFA算法的收敛速度和运行速度都更快。

图2是各算法随机选择一次运行结果的收敛曲线，表现了算法多数情况下的收敛行为。受篇幅限制，仅选择了2个单峰函数( ${f_1}$ 和 ${f_4}$ )和2个多峰函数( ${f_9}$ 和 ${f_{12}}$ )上的收敛曲线。从图2可看出，算法运行早期，FA和OOFA的收敛曲线都急剧下降，说明这个过程算法的求解精度在迅速提高。与FA的收敛曲线相比，OOFA的收敛曲线下降幅度更大，这说明OOFA算法的收敛速度更快。算法运行后期，FA与OOFA的收敛曲线逐渐稳定于某个值，OOFA曲线收敛的值小于FA的，说明OOFA的收敛精度高于FA。

图 2 FA与OOFA在函数f₁, f₄, f₉和f₁₂上的收敛曲线

下载: 全尺寸图片幻灯片

综上所述，对表3和图2的分析证明了OOBL在FA算法中的有效性和适用性。

4.3 OOFA与近期FA改进算法比较

为了验证OOFA的性能，选择近期有代表性的FA变种算法进行比较。比较算法有：MFA^[21], VSSFA^[6], OFA^[12]、RaFA^[8]和ODFA^[9]。为了公平比较，各算法共同的参数设置同4.2节，其它参数与原文献保持一致，即MFA的m=20, OFA的p=0.25。迭代终止条件设为到达最大函数评估次数。表4记录各算法找到的最优解与函数最优值之差的均值(Mean)和标准差(SD)。为了从统计意义上对实验结果进行评价，采用Wilcoxon秩和检验^[22](显著性水平设为0.05)来分析各算法与OOFA在各函数上的结果之间是否存在显著差异，符号“–”，“+”，“≈”分别表示各算法劣于、优于和相当于OOFA的结果。P-value反映OOFA与各算法性能差异的显著性。最后采用Friedman检验^[22]来对算法进行排名。这3项结果记录在表4的最后3行。

表 4 各FA变种算法结果的比较(Mean±SD)

函数	MFA	VSSFA	OFA	RaFA	ODFA	OOFA
f₁	3.58E+04±5.83E+03	3.45E+04±4.31E+03	2.42E+04±5.28E+03	4.03E+02±7.35E+02	1.32E+04±5.63E+03	1.70E–10±8.44E–10
f₂	5.03E+08±1.67E+08	3.73E+08±7.44E+07	3.34E+08±1.65E+08	3.71E+07±2.17E+07	2.19E+08±8.17E+07	3.39E+07±1.04E+07
f₃	1.47E+15±2.87E+15	1.68E+13±2.15E+13	2.01E+14±5.77E+14	2.62E+10±1.55E+10	6.04E+14±2.98E+15	1.61E+09±8.63E+08
f₄	9.27E+04±1.08E+04	8.04E+04±8.81E+03	8.68E+04±1.27E+04	1.04E+05±3.33E+04	8.21E+04±2.27E+04	7.25E+04±1.22E+04
f₅	9.85E+03±4.47E+03	8.56E+03±1.64E+03	5.70E+03±1.94E+03	4.99E+02±1.01E+03	1.14E+03±6.20E+02	1.06E+02±3.32E+01
f₆	5.84E+03±1.72E+03	4.49E+03±5.99E+02	3.48E+03±1.19E+03	1.71E+02±7.17E+01	1.64E+03±1.07E+03	6.90E+01±2.47E+01
f₇	2.52E+04±2.64E+04	2.61E+03±1.28E+03	6.42E+03±1.09E+04	3.03E+04±4.31E+04	2.40E+04±5.81E+04	4.11E+01±1.12E+01
f₈	2.10E+01±6.57E–02	2.10E+01±5.85E–02	2.10E+01±6.54E–02	2.11E+01±5.93E–02	2.10E+01±5.39E–02	2.10E+01±6.09E–02
f₉	4.16E+01±1.81E+00	4.05E+01±9.64E–01	3.83E+01±3.17E+00	3.96E+01±2.48E+00	3.72E+01±3.35E+00	2.14E+01±4.18E+00
f₁₀	5.14E+03±1.10E+03	4.59E+03±5.23E+02	3.29E+03±8.44E+02	1.49E+02±1.23E+02	1.97E+03±9.37E+02	1.67E+01±1.19E+01
f₁₁	6.54E+02±1.11E+02	6.50E+02±4.33E+01	4.60E+02±9.00E+01	1.52E+02±5.41E+01	4.65E+02±9.63E+01	1.13E+01±3.35E+00
f₁₂	7.40E+02±8.81E+01	6.52E+02±4.22E+01	5.13E+02±9.01E+01	8.69E+02±1.54E+02	6.73E+02±1.39E+02	1.05E+02±3.38E+01
f₁₃	7.42E+02±9.14E+01	6.50E+02±5.49E+01	5.48E+02±7.61E+01	8.81E+02±1.31E+02	6.86E+02±9.57E+01	8.64E+01±3.04E+01
f₁₄	7.44E+03±4.96E+02	7.66E+03±2.56E+02	5.83E+03±6.32E+02	1.62E+03±3.60E+02	7.27E+03±6.99E+02	1.55E+03±5.45E+02
f₁₅	7.56E+03±5.92E+02	7.65E+03±3.13E+02	5.72E+03±7.14E+02	4.89E+03±1.01E+03	7.26E+03±4.44E+02	4.41E+03±7.63E+02
f₁₆	2.70E+00±4.78E–01	2.76E+00±3.05E–01	1.47E+00±4.45E–01	1.95E+00±5.61E–01	2.46E+00±4.73E–01	1.79E+00±5.38E–01
f₁₇	1.26E+03±1.41E+02	1.18E+03±8.23E+01	6.52E+02±1.04E+02	9.87E+01±4.59E+01	8.98E+02±1.68E+02	4.09E+01±3.16E+00
f₁₈	1.28E+03±2.00E+02	1.16E+03±9.17E+01	7.18E+02±1.52E+02	1.55E+03±2.47E+02	1.03E+03±1.92E+02	1.06E+02±2.98E+01
f₁₉	2.75E+05±2.01E+05	2.39E+05±6.70E+04	5.00E+04±3.86E+04	7.96E+01±1.68E+02	2.68E+04±5.41E+04	3.34E+00±7.17E–01
f₂₀	1.50E+01±3.72E–02	1.50E+01±2.29E–02	1.50E+01±6.32E–08	1.49E+01±1.78E–01	1.37E+01±8.18E–01	1.50E+01±3.14E–05
f₂₁	3.03E+03±2.98E+02	3.10E+03±1.43E+02	2.47E+03±1.64E+02	4.57E+02±1.71E+02	2.16E+03±3.59E+02	2.92E+02±2.75E+01
f₂₂	8.43E+03±4.74E+02	8.29E+03±2.74E+02	6.77E+03±1.01E+03	2.07E+03±5.70E+02	7.63E+03±9.75E+02	1.91E+03±1.25E+03
f₂₃	8.16E+03±4.96E+02	8.28E+03±2.43E+02	6.82E+03±8.01E+02	6.38E+03±9.46E+02	7.58E+03±6.23E+02	5.61E+03±1.21E+03
f₂₄	3.83E+02±2.26E+01	3.57E+02±8.70E+00	3.45E+02±1.59E+01	3.69E+02±2.90E+01	3.48E+02±1.61E+01	2.17E+02±6.37E+00
f₂₅	4.02E+02±1.31E+01	3.76E+02±6.32E+00	3.85E+02±1.81E+01	3.94E+02±1.78E+01	3.74E+02±1.73E+01	2.70E+02±1.38E+01
f₂₆	2.73E+02±4.82E+01	2.50E+02±1.53E+01	2.62E+02±5.77E+01	3.31E+02±1.08E+02	3.04E+02±9.55E+01	2.95E+02±2.03E+01
f₂₇	1.56E+03±6.16E+01	1.47E+03±3.89E+01	1.41E+03±4.78E+01	1.60E+03±1.07E+02	1.46E+03±9.06E+01	4.51E+02±6.27E+01
f₂₈	5.60E+03±5.24E+02	4.96E+03±2.87E+02	4.56E+03±5.53E+02	6.00E+03±1.08E+03	4.45E+03±6.04E+02	3.00E+02±6.06E–03
–/≈/+	25/2/1	25/2/1	24/2/2	27/0/1	26/1/1	—
P-value	1.18E–5	1.18E–5	1.33E–5	4.46E–6	7.03E–6	—
Friedman	5.30	4.30	3.13	3.61	3.32	1.34

下载: 导出CSV

| 显示表格

从表4可看出，OOFA在大部分函数上都优于各比较算法。从表4中的P-value值均小于0.05，说明OOFA与各比较算法的性能差异非常显著。由Friedman检验排名可知OOFA与各算法相比排名第一。与VSSFA相比，OOFA性能明显更好，这说明OOBL对算法性能提升的贡献高于VSSFA中参数控制的贡献。MFA和RaFA都采用了精英策略。每次迭代中，MFA让最亮萤火虫飞向一个从多个随机方向中找出的最好方向。RaFA则是让最亮萤火虫执行柯西变异。而OOFA中每只萤火虫都有机会执行OOBL，可以探索不同的反向空间，相比MFA和RaFA, OOFA具有更强的全局搜索能力。OFA与ODFA也采用了反向学习策略。OFA算法仅在 ${f_{16}}$ 和 ${f_{26}}$ 上表现优于OOFA。它用最差萤火虫的反向个体和最优个体依概率替换最差萤火虫，这种策略对群体逃离局部最优有一定作用，但它只利用了最差个体的反向空间，没有探索更多优秀个体的反向空间；而且最差个体的反向个体不一定在每一维上的信息都较差。所以，OFA算法探索的反向空间是非常有限的，且没有充分聚集最差个体和其反向个体中的有用信息。ODFA仅在 ${f_{20}}$ 上表现优于OOFA，它仅在种群初始过程中利用反向学习获得更好的初始种群，而迭代过程中，在不同维上结合了不同个体所包含的有利信息，没有利用反向个体中的有利信息。OOFA在24个函数上优于OFA，在26个函数上优于ODFA。这说明OOFA中的OOBL策略不但利用反向学习充分探索了反向空间，而且利用正交试验设计结合并保存个体和反向个体中有用信息的组合。此外，OFA和ODFA采用的反向学习策略是OBL，我们之前的研究^[23]发现，OBL容易造成搜索偏向坐标，在带偏移的函数上往往表现不佳。而OOFA采用的是CO，没有坐标搜索偏向，所以在复杂的CEC 2013测试函数上能表现出更好的收敛性。

基于以上实验结果和统计分析，可得出在CEC 2013测试集上，OOFA算法性能明显优于其它比较算法。

5. 结束语

本文利用反向学习和正交试验设计构造了一种正交反向学习策略OOBL，并应用到FA中，提出了一种改进的萤火虫算法OOFA。OOFA的特点主要是利用正交试验设计充分挖掘和保存个体与反向个体中的有用信息，从而提高算法性能。OOFA保持了FA算法的基本框架，没有增加额外参数，仅在群体中随机选择的一个个体上执行OOBL。本文从理论上分析了OOFA的优越性，且从实验和统计分析上表明OOBL策略的有效性和OOFA的较优性能。后续工作是将OOBL策略引入其它群智能算法中并用于解决命名数据网络中的路由优化等问题。

图 1 概率图模型

下载: 全尺寸图片幻灯片

图 2 稀疏向量θ

下载: 全尺寸图片幻灯片

图 3 3种算法相应相变图

下载: 全尺寸图片幻灯片

图 4 3种算法平均重构误差随SNR变化曲线

下载: 全尺寸图片幻灯片

图 5 目标散射点分布图

下载: 全尺寸图片幻灯片

图 6 速度加速度估计误差随SNR变化曲线

下载: 全尺寸图片幻灯片

图 7 仿真数据波形1成像结果

下载: 全尺寸图片幻灯片

图 8 仿真数据波形2成像结果

下载: 全尺寸图片幻灯片

图 9 飞机全频带实测数据成像结果

下载: 全尺寸图片幻灯片

图 10 飞机实测数据波形1成像结果

下载: 全尺寸图片幻灯片

图 11 飞机实测数据波形2成像结果

下载: 全尺寸图片幻灯片

表 1 所提算法伪代码

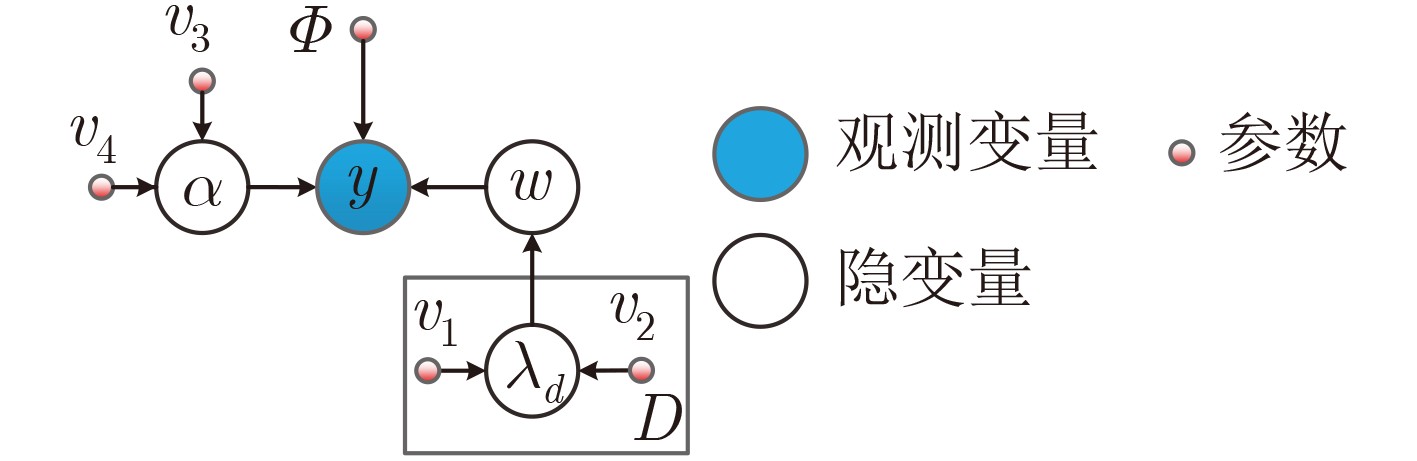
算法：基于稀疏步进调频信号的低信噪比ISAR成像
(1) 初始化种群 $\left( {\Delta {{\hat v}_{\rm{R}}},\Delta {{\hat a}_{\rm{R}}}} \right)$ , ${v_1}$ , ${v_2}$ , ${v_3}$ , ${v_4}$ , ${\boldsymbol{\varLambda}}$ , $\alpha$ , ${{{G}}_{\rm{1}}}$ , ${{{G}}_{\rm{2}}}$ , ${\eta _1}$ 。
(2) For iter1=1: ${{{G}}_{\rm{1}}}$
(a) For k=1: ${{K}}$
构造 ${\boldsymbol{D}}_k^{\left( {{\rm{iter1}}} \right)}\left( {\Delta {{\hat v}_{\rm{R}}},\Delta {{\hat a}_{\rm{R}}}} \right)$ ；
For iter2=1: ${{{G}}_{\rm{2}}}$
利用式(22)更新 $\alpha$ ；
利用式(24)更新 ${\boldsymbol{\varLambda}}$ ；
利用式(26)更新 ${\boldsymbol{\theta}}$ ；
若 $\hat {\boldsymbol{\theta}} _k^{\left( {{\rm{iter1}}} \right)}$ 相对于前一次估计的变化量小于 ${\eta _1}$ 则停止循环；
End
End
(b) 构建距离像矩阵 ${\boldsymbol{s} }_{\rm{r} }^{\left( { {\rm{iter1} } } \right)}\left( {\Delta { {\hat v}_{\rm{R} } },\Delta { {\hat a}_{\rm{R} } } } \right) = \left[ { {\boldsymbol{\theta} } _{\rm{1} }^{\left( { {\rm{iter1} } } \right)},{\boldsymbol{\theta} } _{\rm{2} }^{\left( { {\rm{iter1} } } \right)}, \cdots,{\boldsymbol{\theta} } _K^{\left( { {\rm{iter1} } } \right)} } \right]$ ，得 ${I^{\left( {{\rm{iter1}}} \right)}}\left( {\Delta {{\hat v}_{\rm{R}}},\Delta {{\hat a}_{\rm{R}}}} \right)$ ；
(c) 根据式(18)计算图像熵；
(d) 保留图像熵较小的个体并更新种群；
(e) 判断是否达到循环次数 ${{{G}}_{\rm{1}}}$ ；
End
(3) 实现高分辨ISAR成像。

下载: 导出CSV

表 2 运算复杂度对比

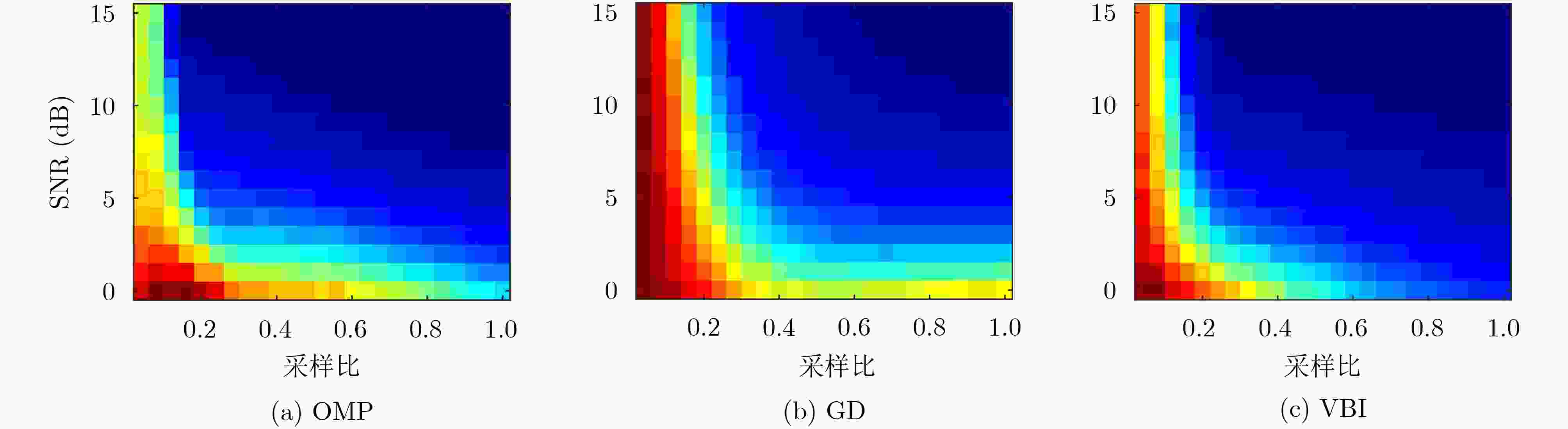
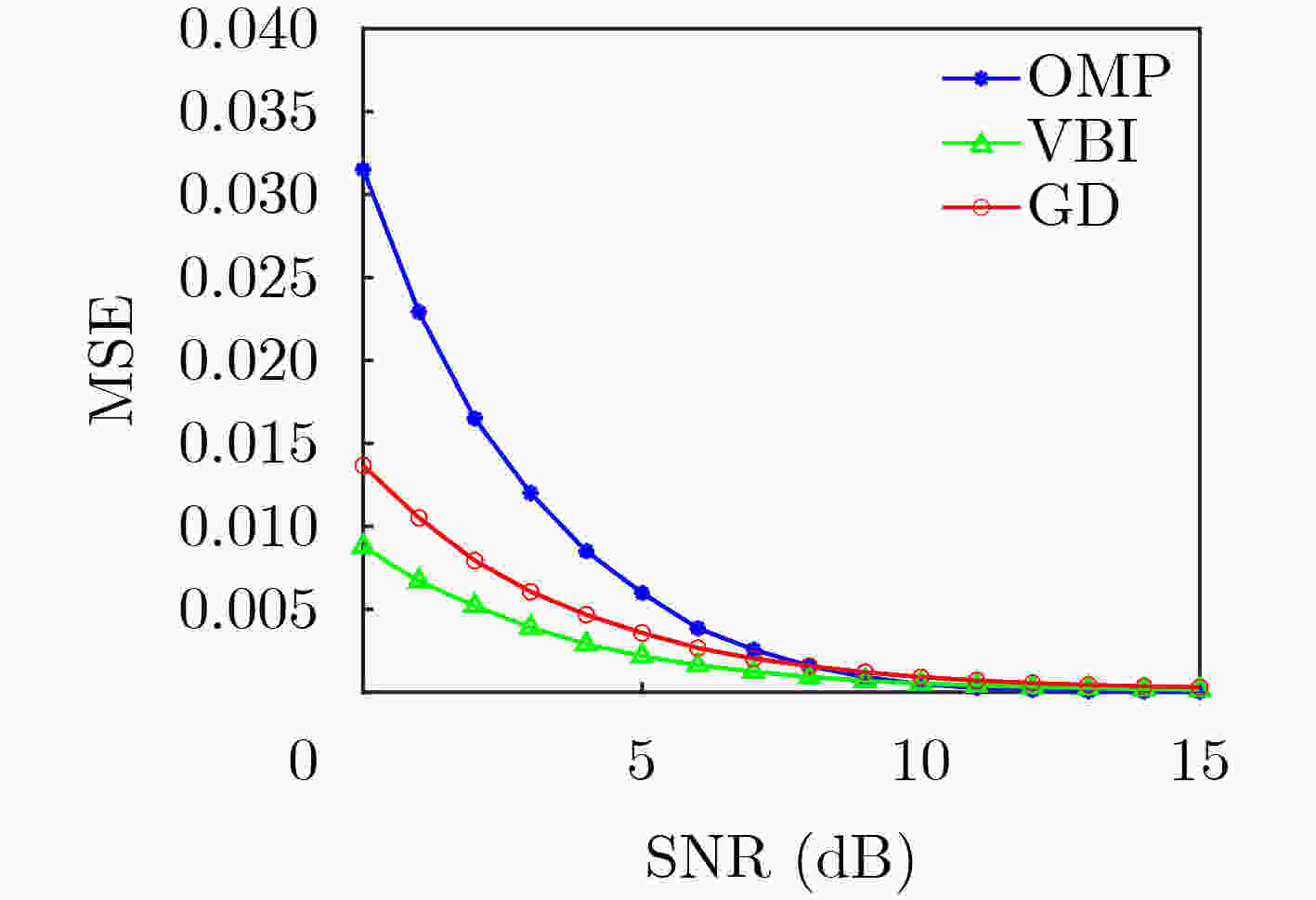
重构算法	OMP	GD	VBI
运算复杂度	${\cal{O}}\left( {{k_0}{L^2}} \right)$	${\cal{O}}\left( {{L^{\rm{3}}}} \right)$	${\cal{O}}\left( {{L^{\rm{3}}}} \right)$

下载: 导出CSV

表 3 雷达系统参数

${f_{\rm{c}}}$	${\rm{PRF}}$	${T_{\rm{R}}}$	$B$	$\Delta f$
10 GHz	6.4 kHz	20 μs	800 MHz	10 MHz

下载: 导出CSV

表 4 Yak-42飞机剩余速度估计值表

	本文算法	算法1
波形1(m/s)	9.9763	9.8973
波形2(m/s)	9.9619	9.7503

下载: 导出CSV

表 5 Yak-42飞机剩余加速度估计值表

	本文算法	算法1
波形1(m/s²)	0.9975	1.1147
波形2(m/s²)	0.9994	1.2095

下载: 导出CSV

表 6 不同算法对Yak-42飞机实测数据成像的图像熵

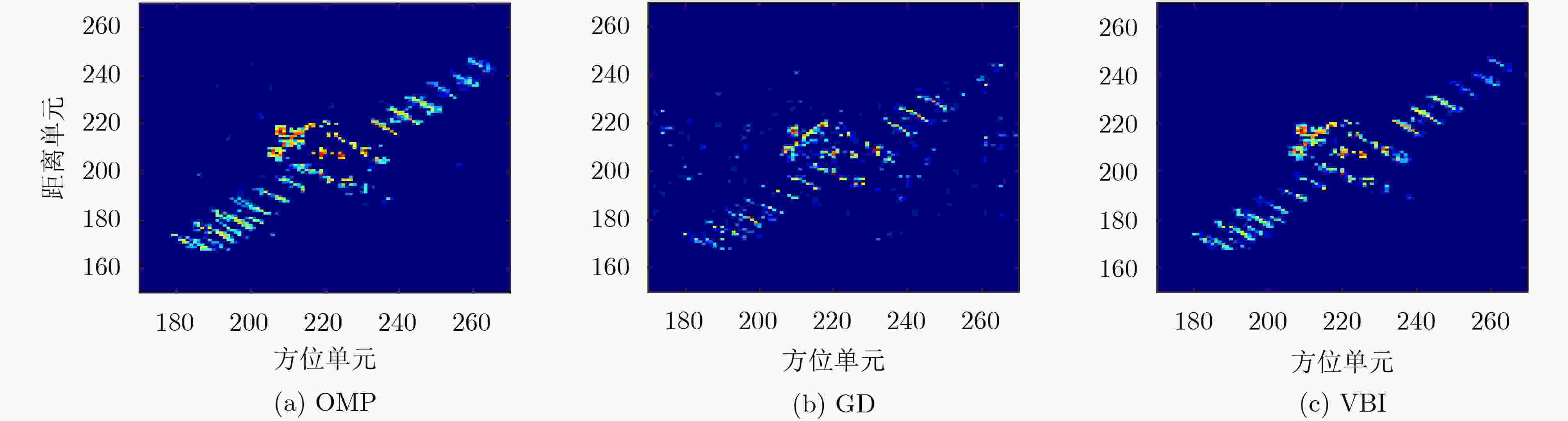
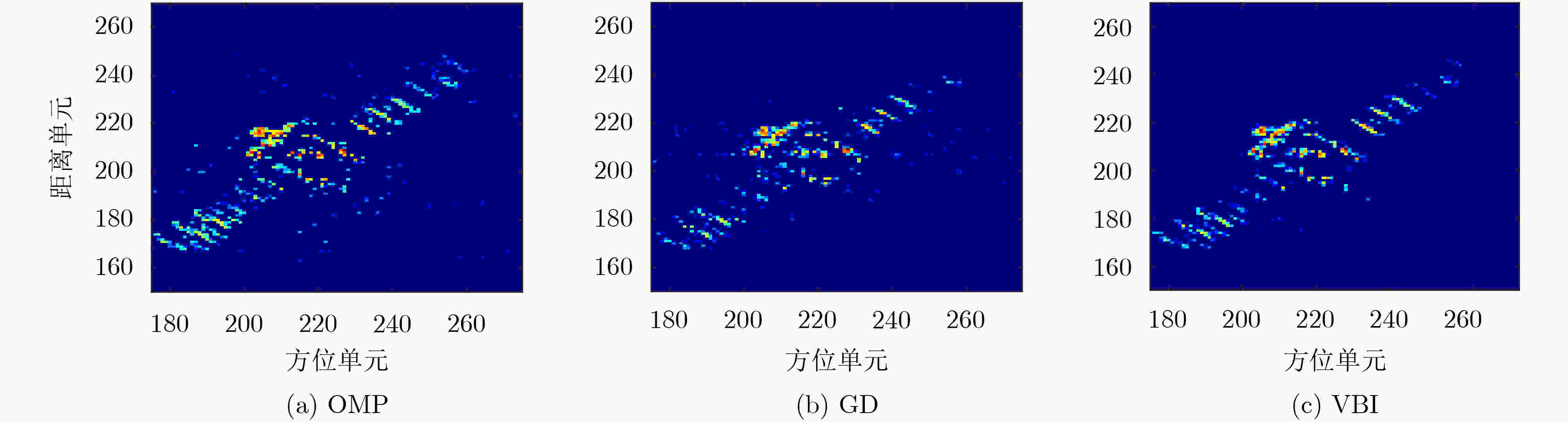
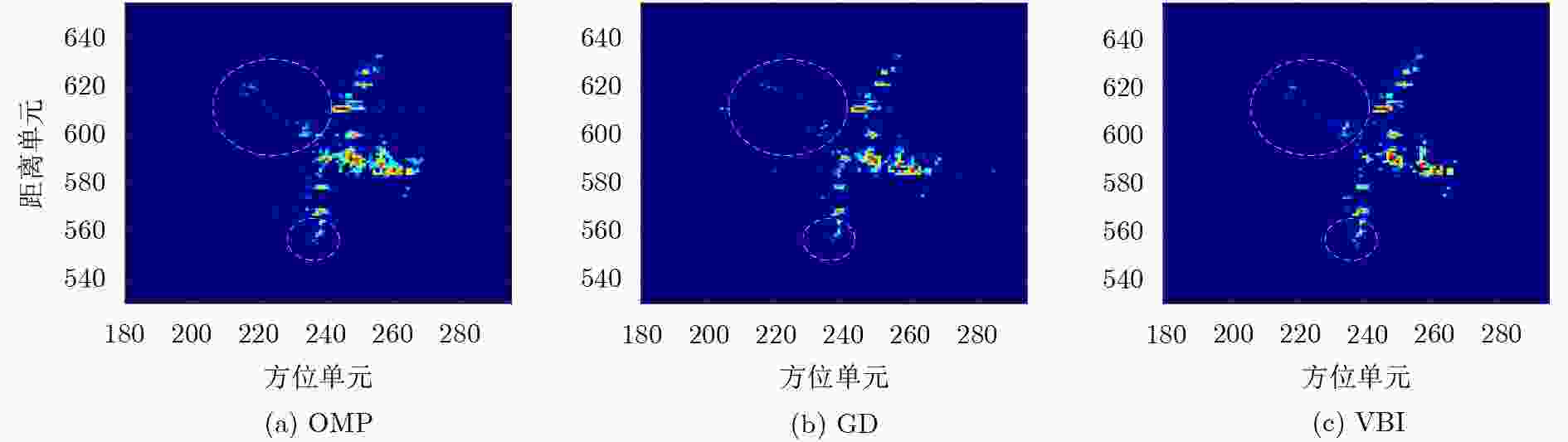
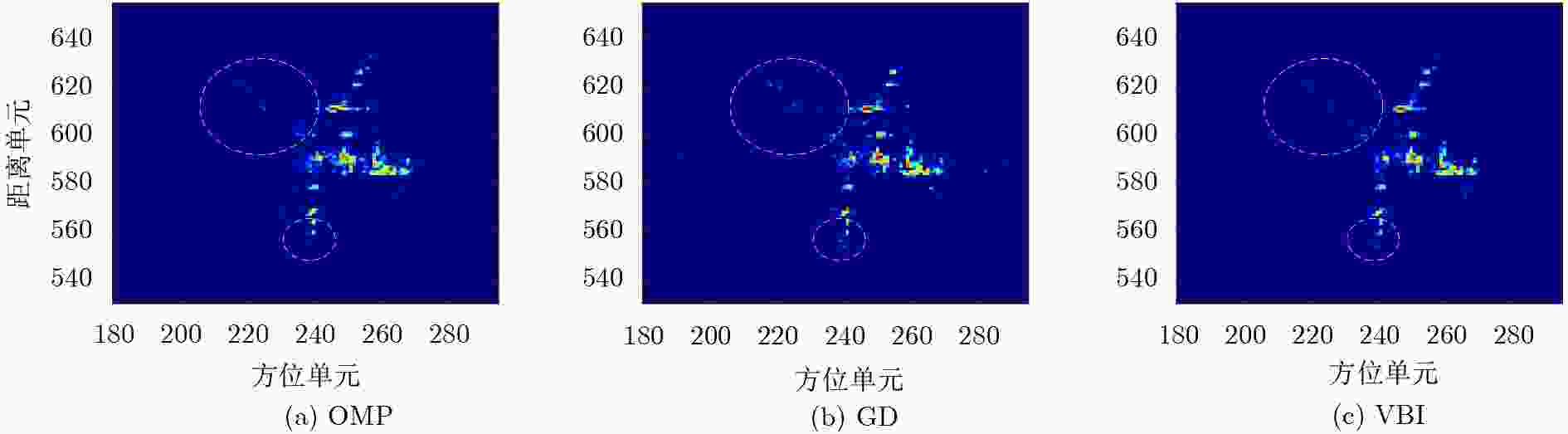
	OMP	GD	VBI
波形1	0.2757	0.2108	0.1963
波形2	0.2086	0.1957	0.1767

下载: 导出CSV

参考文献(20)

[1]	BAI Xueru, ZHOU Xuening, ZHANG Feng, et al. Robust pol-ISAR target recognition based on ST-MC-DCNN[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(12): 9912–9927. doi: 10.1109/TGRS.2019.2930112
[2]	王天云, 陆新飞, 孙麟, 等. 基于贝叶斯压缩感知的ISAR自聚焦成像[J]. 电子与信息学报, 2015, 37(11): 2719–2726. doi: 10.11999/JEIT150235 WANG Tianyun, LU Xinfei, SUN Lin, et al. An autofocus imaging method for ISAR based on Bayesian compressive sensing[J]. Journal of Electronics &Information Technology, 2015, 37(11): 2719–2726. doi: 10.11999/JEIT150235
[3]	LUO Ying, ZHANG Qun, QIU Chengwei, et al. Micro-Doppler effect analysis and feature extraction in ISAR imaging with stepped-frequency chirp signals[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(4): 2087–2098. doi: 10.1109/TGRS.2009.2034367
[4]	ZHANG Lei, XING Mengdao, QIU Chengwei, et al. Resolution enhancement for inversed synthetic aperture radar imaging under low SNR via improved compressive sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(10): 3824–3838. doi: 10.1109/TGRS.2010.2048575
[5]	FU Wei, JIANG Defu, GAO Yiyue, et al. An adaptive optimal waveform design algorithm based on frequency-stepped chirp signal[J]. IET Radar, Sonar & Navigation, 2019, 13(6): 892–899. doi: 10.1049/iet-rsn.2018.5410
[6]	WEI Shaopeng, ZHANG Lei, MA Hui, et al. Sparse frequency waveform optimization for high-resolution ISAR imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(1): 546–566. doi: 10.1109/TGRS.2019.2937965
[7]	JEONG H R, KIM H T, and KIM K T. Application of subarray averaging and entropy minimization algorithm to stepped-frequency ISAR autofocus[J]. IEEE Transactions on Antennas and Propagation, 2008, 56(4): 1144–1154. doi: 10.1109/TAP.2008.919208
[8]	LIU Yabo, XING Mengdao, ZHANG Leiyong, et al. Novel range profile synthesis algorithm for linearly stepped-frequency modulated inversed synthetic aperture radar imaging of remote manoeuvring target[J]. IET Radar, Sonar & Navigation, 2011, 5(4): 496–506. doi: 10.1049/iet-rsn.2010.0013
[9]	LIAO Zhikun, HU Jiemin, LU Dawei, et al. Motion analysis and compensation method for random stepped frequency radar using the pseudorandom code[J]. IEEE Access, 2018, 6: 57643–57654. doi: 10.1109/ACCESS.2018.2873784
[10]	KANG M S, LEE S J, LEE S H, et al. ISAR imaging of high-speed maneuvering target using gapped stepped-frequency waveform and compressive sensing[J]. IEEE Transactions on Image Processing, 2017, 26(10): 5043–5056. doi: 10.1109/TIP.2017.2728182
[11]	李瑞, 张群, 苏令华, 等. 基于稀疏贝叶斯学习的双基雷达关联成像[J]. 电子与信息学报, 2019, 41(12): 2865–2872. doi: 10.11999/JEIT180933 LI Rui, ZHANG Qun, SU Linghua, et al. Bistatic radar coincidence imaging based on sparse Bayesian learning[J]. Journal of Electronics &Information Technology, 2019, 41(12): 2865–2872. doi: 10.11999/JEIT180933
[12]	BAI Xueru, ZHANG Yu, and ZHOU Feng. High-resolution radar imaging in complex environments based on Bayesian learning with mixture models[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(2): 972–984. doi: 10.1109/TGRS.2018.2863743
[13]	LI Yuanyuan, FU Yaowen, and ZHANG Wenpeng. High-resolution distributed ISAR imaging by OMP method[J]. The Journal of Engineering, 2019, 2019(19): 6138–6142. doi: 10.1049/joe.2019.0380
[14]	ZHU Feng, ZHANG Qun, LEI Qiang, et al. Reconstruction of moving target’s HRRP using sparse frequency-stepped chirp signal[J]. IEEE Sensors Journal, 2011, 11(10): 2327–2334. doi: 10.1109/JSEN.2011.2136375
[15]	ZHANG Lei, QIAO Zhijun, XING Mengdao, et al. High-resolution ISAR imaging with sparse stepped-frequency waveforms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11): 4630–4651. doi: 10.1109/TGRS.2011.2151865
[16]	ZHANG Shuanghui, LIU Yongxiang, LI Xiang, et al. Bayesian high resolution range profile reconstruction of high-speed moving target from under-sampled data[J]. IEEE Transactions on Image Processing, 2020, 29: 5110–5120. doi: 10.1109/TIP.2020.2980149
[17]	NING Yu, BAI Xueru, ZHOU Feng, et al. Method for inverse synthetic aperture radar imaging of space debris using improved genetic algorithm[J]. IET Radar, Sonar & Navigation, 2017, 11(5): 812–821. doi: 10.1049/iet-rsn.2016.0048
[18]	SUN Lin and CHEN Weidong. Improved Bayesian ISAR imaging by learning the local structures of the target scene[J]. IEEE Sensors Journal, 2019, 19(19): 8865–8877. doi: 10.1109/JSEN.2019.2919572
[19]	ZHOU Feng, BAI Xueru, XING Mengdao, et al. Analysis of wide-angle radar imaging[J]. IET Radar, Sonar & Navigation, 2011, 5(4): 449–457. doi: 10.1049/iet-rsn.2010.0076
[20]	杨磊, 夏亚波, 毛欣瑶, 等. 基于分层贝叶斯Lasso的稀疏ISAR成像算法[J]. 电子与信息学报, 2021, 43(3): 623–631. doi: 10.11999/JEIT200292 YANG Lei, XIA Yabo, MAO Xinyao, et al. Sparse ISAR imaging algorithm based on Bayesian-lasso[J]. Journal of Electronics &Information Technology, 2021, 43(3): 623–631. doi: 10.11999/JEIT200292

施引文献

期刊类型引用(13)

1.	黄亮，张军，季伟东. 结合正交补空间反向学习策略的自然计算方法. 小型微型计算机系统. 2023(03): 544-552 . 百度学术
2.	韩沐枫. 计及需求响应的微电网多时间尺度调度仿真. 计算机与现代化. 2023(03): 102-106 . 百度学术
3.	王文川，徐雷，徐冬梅. 阴阳萤火虫算法及其在全局优化问题中的应用研究. 应用基础与工程科学学报. 2022(01): 64-75 . 百度学术
4.	李钧超，张辰，陈丹，巩鑫龙. 考虑多站融合的智能变电站选址定容优化方法研究. 电网与清洁能源. 2022(03): 61-67 . 百度学术
5.	王天雷，张绮媚，李俊辉，周京，刘人菊，谭南林. 基于正交对立学习的改进麻雀搜索算法. 电子测量技术. 2022(10): 57-66 . 百度学术
6.	赵新超，熊卿，冯帅. 均匀邻域对位的自适应差分进化算法. 集美大学学报(自然科学版). 2021(01): 72-81 . 百度学术
7.	郭腾，陈剑培，况富强. 基于改进的和声搜索算法的无线通信频谱分配策略研究. 微型电脑应用. 2021(03): 97-99+105 . 百度学术
8.	李媛媛，魏延，张文泷，王晶仪，蒋俊蕊. 基于K-means的邻域结合随机吸引的萤火虫算法. 重庆师范大学学报(自然科学版). 2021(06): 114-121 . 百度学术
9.	刘浩洋，杜欣慧，裴玥瑶，李钢. 针对漂浮式光伏电站最大功率追踪的研究. 电源技术. 2020(01): 72-75 . 百度学术
10.	刘小龙. 基于统计指导的飞蛾扑火算法求解大规模优化问题. 控制与决策. 2020(04): 901-908 . 百度学术
11.	李煜，郑娟，刘景森. 大规模优化问题的改进花朵授粉算法. 计算机科学与探索. 2020(08): 1427-1440 . 百度学术
12.	钟章生，陈世炉，陈志龙. 利用并行惯性权重OOL-FA的大数据分类. 计算机工程与设计. 2020(10): 2818-2824 . 百度学术
13.	厉建军，张建梅，孙晓红，王迎迎，李洋，辛伟娟，王彩虹. 卤煮工艺对酱卤肉制品品质的影响. 农产品加工. 2019(13): 52-54+58 . 百度学术

其他类型引用(7)

资源附件(0)

访问统计

图(11) / 表(6)

计量

文章访问数: 1251
HTML全文浏览量: 463
PDF下载量: 131
被引次数: 20

1. 引言
2. 萤火虫算法与反向学习
2.1 萤火虫算法FA
2.2 反向学习
3. 正交反向学习萤火虫算法OOFA
3.1 正交反向学习策略
3.2 OOFA算法
4. 仿真实验与结果分析
4.1 测试函数
4.2 OOBL策略有效性分析
4.3 OOFA与近期FA改进算法比较
5. 结束语

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

基于稀疏步进调频信号的低信噪比逆合成孔径雷达成像

doi: 10.11999/JEIT210056

作者简介:
王樾：男，1995年生，硕士，研究方向为ISAR成像

白雪茹：女，1984年生，教授，研究方向为高分辨雷达成像、雷达目标识别

周峰：男，1980年生，教授，研究方向为电子对抗、雷达成像

通讯作者:
周峰　fzhou@mail.xidian.edu.cn

计量

High-resolution Inverse Synthetic Aperture Radar Imaging with Sparse Stepped-frequency Chirp Signals under Low Signal to Noise Ratio

1. 引言

2. 萤火虫算法与反向学习

2.1 萤火虫算法FA

2.2 反向学习

3. 正交反向学习萤火虫算法OOFA

3.1 正交反向学习策略

3.2 OOFA算法

4. 仿真实验与结果分析

4.1 测试函数

4.2 OOBL策略有效性分析

4.3 OOFA与近期FA改进算法比较

5. 结束语

期刊类型引用(13)

其他类型引用(7)

计量

目录

1. 引言

2. 萤火虫算法与反向学习

2.1 萤火虫算法FA

2.2 反向学习

3. 正交反向学习萤火虫算法OOFA

3.1 正交反向学习策略

3.2 OOFA算法

4. 仿真实验与结果分析

4.1 测试函数

4.2 OOBL策略有效性分析

4.3 OOFA与近期FA改进算法比较

5. 结束语

留言板

基于稀疏步进调频信号的低信噪比逆合成孔径雷达成像

doi: 10.11999/JEIT210056

作者简介: 王樾：男，1995年生，硕士，研究方向为ISAR成像 白雪茹：女，1984年生，教授，研究方向为高分辨雷达成像、雷达目标识别 周峰：男，1980年生，教授，研究方向为电子对抗、雷达成像

通讯作者: 周峰 fzhou@mail.xidian.edu.cn

计量

出版历程

High-resolution Inverse Synthetic Aperture Radar Imaging with Sparse Stepped-frequency Chirp Signals under Low Signal to Noise Ratio

1. 引言

2. 萤火虫算法与反向学习

2.1 萤火虫算法FA

2.2 反向学习

3. 正交反向学习萤火虫算法OOFA

3.1 正交反向学习策略

3.2 OOFA算法

4. 仿真实验与结果分析

4.1 测试函数

4.2 OOBL策略有效性分析

4.3 OOFA与近期FA改进算法比较

5. 结束语

期刊类型引用(13)

其他类型引用(7)

计量

出版历程

目录

1. 引言

2. 萤火虫算法与反向学习

2.1 萤火虫算法FA

2.2 反向学习

3. 正交反向学习萤火虫算法OOFA

3.1 正交反向学习策略

3.2 OOFA算法

4. 仿真实验与结果分析

4.1 测试函数

4.2 OOBL策略有效性分析

4.3 OOFA与近期FA改进算法比较

5. 结束语

作者简介:
王樾：男，1995年生，硕士，研究方向为ISAR成像

白雪茹：女，1984年生，教授，研究方向为高分辨雷达成像、雷达目标识别

周峰：男，1980年生，教授，研究方向为电子对抗、雷达成像

通讯作者:
周峰　fzhou@mail.xidian.edu.cn