Gridless DOA Estimation Algorithm for Planar Arrays with Arbitrary Geometry
-
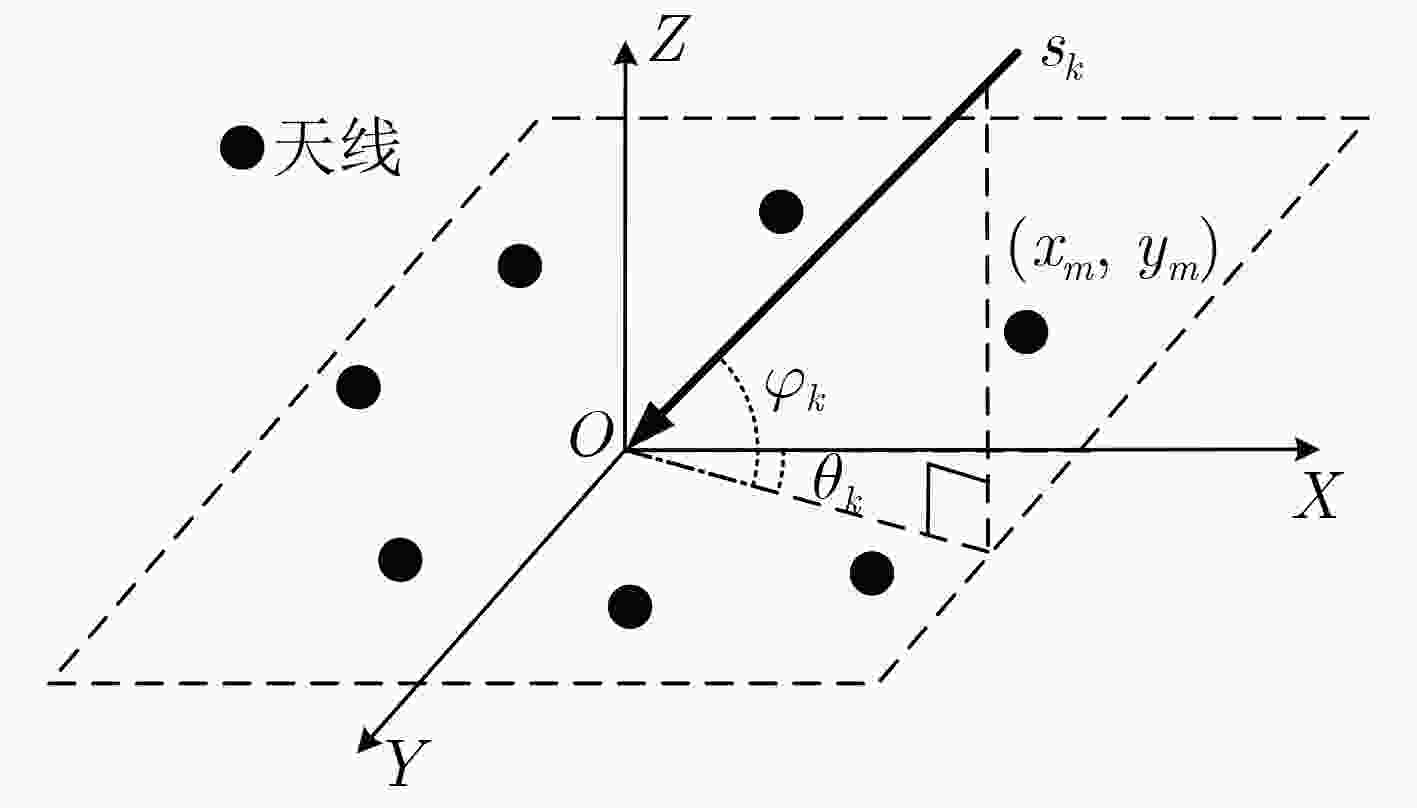
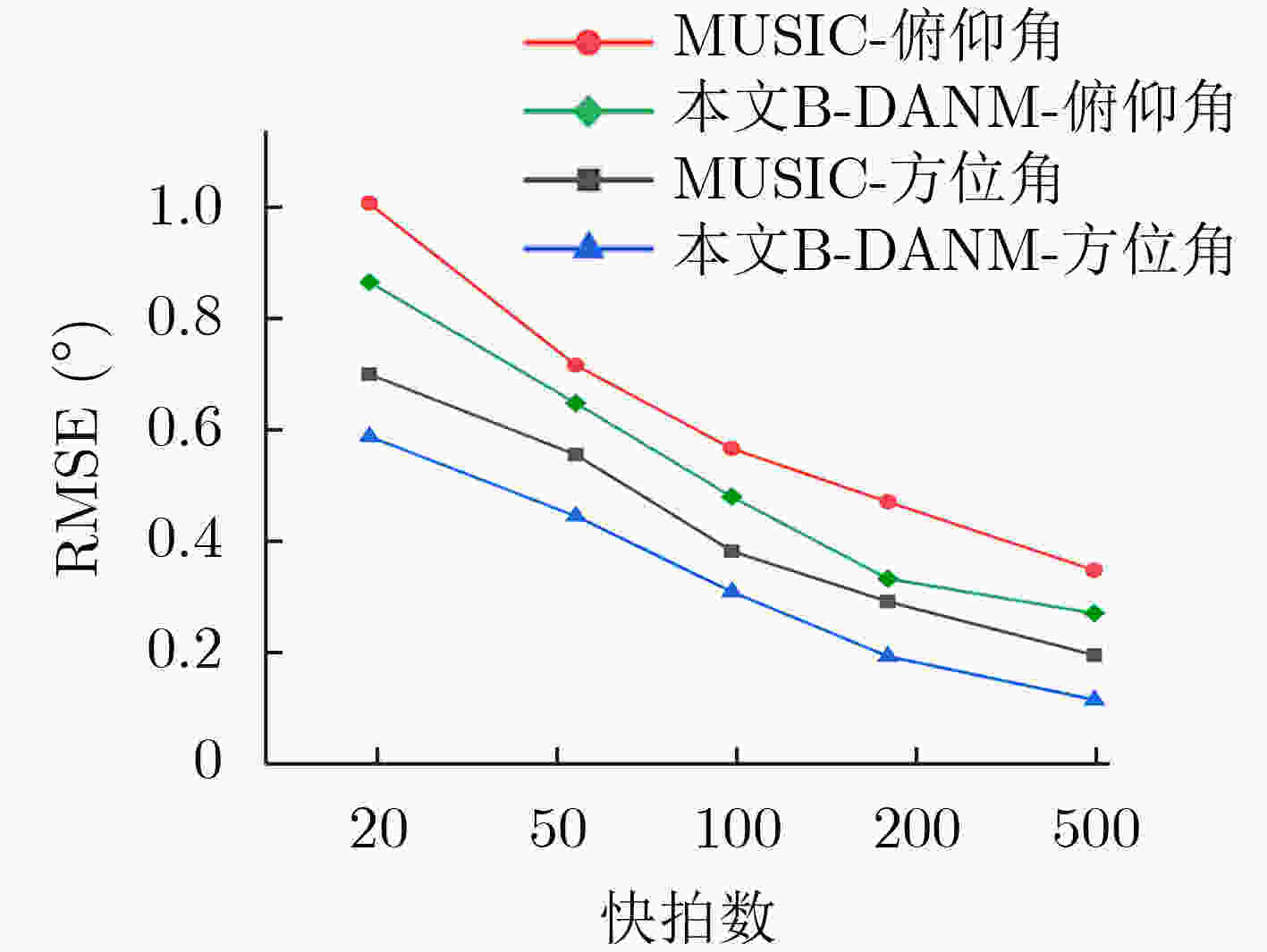
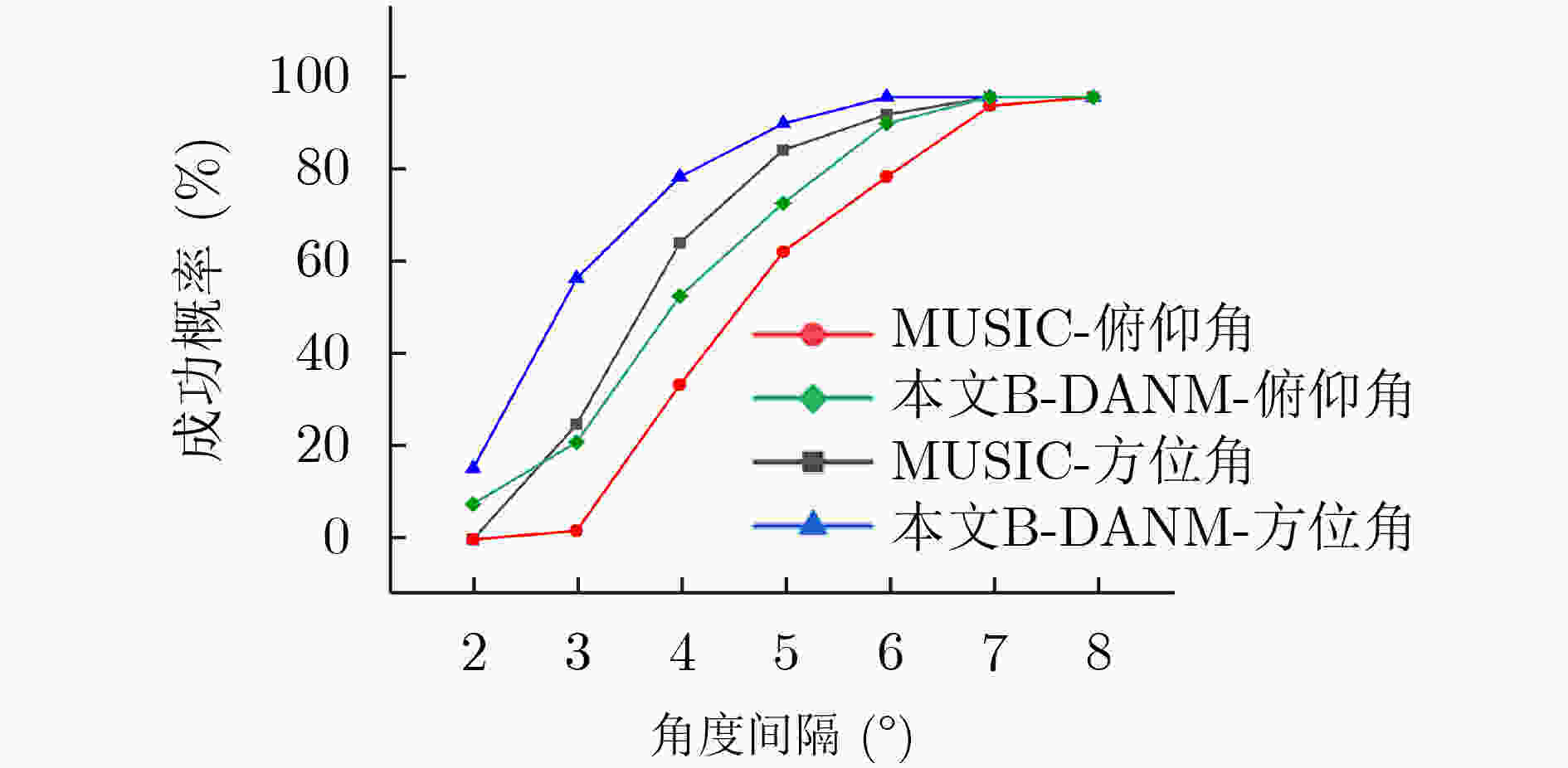
摘要: 由于在网格失配情况下依然具备良好的估计性能,无网格DOA估计算法近年来受到了广泛的关注与研究,其中又以基于原子范数最小化(ANM)的DOA估计算法最具代表性。随着可分离ANM(DANM)算法的提出,为ANM理论在2维DOA估计领域中的应用提供了可能。不过传统的DANM算法以及其后续的一系列改进算法都只适用于均匀矩形阵列(URA)或稀疏矩形阵列(SRA),无法适用于具有任意几何结构的平面阵列。针对上述问题,该文提出一种适用于任意几何结构平面阵列的无网格DOA估计算法,即B-DANM算法。该算法利用一类贝塞尔函数对实际平面天线阵列接收信号的协方差数据进行展开,从而获得适用于任意几何结构平面阵列的DANM算法框架,然后再通过求解半定规划问题、Toeplitz矩阵的Vandermonde分解以及估计参数配对、角度变换等过程来得到最终的DOA估计结果。仿真实验验证了,在任意几何结构平面阵列的测向系统中,B-DANM算法相比于传统的2维DOA估计算法在精度、分辨力等方面的优势。
-
关键词:
- 无网格DOA估计算法 /
- 原子范数最小化 /
- 半定规划 /
- 一类贝塞尔函数
Abstract: Due to the good estimation performance in the case of off-grid, the gridless DOA estimation algorithms attract extensive attentions and researches in recent years, among which the most representative is the one based on Atomic Norm Minimization (ANM). With the development of Decoupled ANM (DANM) algorithm, the application of ANM to the field of two-dimensional DOA estimation is possible. However, the traditional DANM algorithm and its subsequent improved algorithms are only suitable for Uniform Rectangular Array (URA) or Sparse Rectangular Array (SRA), and is not suitable for planar arrays with arbitrary geometry. In order to solve the above problem, a gridless DOA estimation algorithm, B-DANM algorithm, is proposed for planar arrays with arbitrary geometry. B-DANM algorithm exploits the first Bessel function to expand the covariance data of the received signal of the actual planar antenna array, so as to obtain the DANM algorithm framework suitable for planar arrays with arbitrary geometry, and then the final DOA estimation result is obtained by solving the Semi-Definite Program (SDP) problem, Vandermonde decomposition of Toeplitz matrix, pairing of estimation parameters and angle transformation. The simulation results show that the B-DANM algorithm has the advantages of accuracy and resolution compared with the traditional two-dimensional DOA estimation algorithm in the direction finding system of planar arrays with arbitrary geometry. -
表 1 B-DANM算法
输入:阵列接收数据${\boldsymbol{Z}}$,阵元位置坐标集合$\mathbb{D}$,贝塞尔函数最大
阶数$Q$,正则化参数$\varepsilon $;步骤1 计算协方差矩阵${\boldsymbol{\hat R} } = {\boldsymbol{Z} }{ {\boldsymbol{Z} }^{\rm{H}}}/{\boldsymbol{T} }$; 步骤2 根据式(12)构造矩阵${{\boldsymbol{G}}_x}$与${{\boldsymbol{G}}_y}$; 步骤3 求解式(18)所示的半定规划问题; 步骤4 对${\boldsymbol{T}}({{\boldsymbol{u}}_x})$与${\boldsymbol{T}}({{\boldsymbol{u}}_y})$做Vandermonde分解,得到参数
${\alpha _k}$与${\beta _k}$的估计结果;步骤5 对参数${\alpha _k}$与${\beta _k}$的估计结果进行配对; 步骤6 根据式(8)所示的参数关系,得到最终的DOA估计结
果${\hat \theta _k}$与${\hat \varphi _k}$;表 2 算法复杂度分析
算法 复杂度 2D-MUSIC $O\left( {{M^2}\left( {T + {P_1}{P_2}} \right) + {M^3}} \right)$ DANM $O\left( {{{\left( {{M_x} + {M_y}} \right)}^{3.5}}\lg (1/\rho )} \right)$ CPPA-DANM $O\left( {{{\left( {2{x_{\max }} + 2{y_{\max }}} \right)}^{3.5}}\lg (1/\rho )} \right)$ B-DANM $O\left( {{{\left( {4Q + 2} \right)}^{3.5}}\lg (1/\rho )} \right)$ -
[1] 张海, 陈小龙, 张涛, 等. 基于MUSIC算法的二次雷达应答信号分离方法[J]. 电子与信息学报, 2020, 42(12): 2984–2991. doi: 10.11999/JEIT190842ZHANG Hai, CHEN Xiaolong, ZHANG Tao, et al. Overlapping secondary surveillance radar replies separation algorithm based on MUSIC[J]. Journal of Electronics &Information Technology, 2020, 42(12): 2984–2991. doi: 10.11999/JEIT190842 [2] 李建峰, 沈明威, 蒋德富. 互质阵中基于降维求根的波达角估计算法[J]. 电子与信息学报, 2018, 40(8): 1853–1859. doi: 10.11999/JEIT171087LI Jianfeng, SHEN Mingwei, and JIANG Defu. Reduced- dimensional root finding based direction of arrival estimation for coprime array[J]. Journal of Electronics &Information Technology, 2018, 40(8): 1853–1859. doi: 10.11999/JEIT171087 [3] SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830 [4] ROY R and KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 984–995. doi: 10.1109/29.32276 [5] CANDES E J, ROMBERG J, and TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489–509. doi: 10.1109/TIT.2005.862083 [6] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. doi: 10.1109/TIT.2006.871582 [7] CANDES E J and WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21–30. doi: 10.1109/MSP.2007.914731 [8] BARANIUK R G. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118–121. doi: 10.1109/MSP.2007.4286571 [9] MALIOUTOV D, CETIN M, and WILLSKY A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Transactions on Signal Processing, 2005, 53(8): 3010–3022. doi: 10.1109/TSP.2005.850882 [10] CHI Y, SCHARF L L, PEZESHKI A, et al. Sensitivity to basis mismatch in compressed sensing[J]. IEEE Transactions on Signal Processing, 2011, 59(5): 2182–2195. doi: 10.1109/TSP.2011.2112650 [11] DAS A. Theoretical and experimental comparison of off-grid sparse Bayesian direction-of-arrival estimation algorithms[J]. IEEE Access, 2017, 5: 18075–18087. doi: 10.1109/ACCESS.2017.2747153 [12] YANG Zai, XIE Lihua, and ZHANG Cishen. Off-grid direction of arrival estimation using sparse Bayesian inference[J]. IEEE Transactions on Signal Processing, 2013, 61(1): 38–43. doi: 10.1109/TSP.2012.2222378 [13] CHANDRASEKARAN V, RECHT B, PARRILO P A, et al. The convex geometry of linear inverse problems[J]. Foundations of Computational Mathematics, 2012, 12(6): 805–849. doi: 10.1007/s10208-012-9135-7 [14] CANDÈS E J and FERNANDEZ-GRANDA C. Towards a mathematical theory of super-resolution[J]. Communications on Pure and Applied Mathematics, 2014, 67(6): 906–956. doi: 10.1002/cpa.21455 [15] TANG Gongguo, BHASKAR B N, SHAH P, et al. Compressed sensing off the grid[J]. IEEE Transactions on Information Theory, 2013, 59(11): 7465–7490. doi: 10.1109/TIT.2013.2277451 [16] BHASKAR B N, TANG Gongguo, and RECHT B. Atomic norm denoising with applications to line spectral estimation[J]. IEEE Transactions on Signal Processing, 2013, 61(23): 5987–5999. doi: 10.1109/TSP.2013.2273443 [17] YANG Yang, CHU Zhigang, XU Zhongming, et al. Two-dimensional grid-free compressive beamforming[J]. The Journal of the Acoustical Society of America, 2017, 142(2): 618–629. doi: 10.1121/1.4996460 [18] YANG Yang, CHU Zhigang, and PING Guoli. Alternating direction method of multipliers for weighted atomic norm minimization in two-dimensional grid-free compressive beamforming[J]. The Journal of the Acoustical Society of America, 2018, 144(5): EL361–EL366. doi: 10.1121/1.5066345 [19] YANG Yang, CHU Zhigang, and PING Guoli. Two-dimensional multiple-snapshot grid-free compressive beamforming[J]. Mechanical Systems and Signal Processing, 2019, 124: 524–540. doi: 10.1016/j.ymssp.2019.02.011 [20] ZHANG Zhe, WANG Yue, and TIAN Zhi. Efficient two-dimensional line spectrum estimation based on decoupled atomic norm minimization[J]. Signal Processing, 2019, 163: 95–106. doi: 10.1016/j.sigpro.2019.04.024 [21] TIAN Xiyan, LEI Jinhui, and DU Liufeng. A generalized 2-D DOA estimation method based on low-rank matrix reconstruction[J]. IEEE Access, 2018, 6: 17407–17414. doi: 10.1109/ACCESS.2018.2820165 [22] LU Aihong, GUO Yan, LI Ning, et al. Efficient gridless 2-D direction-of-arrival estimation for coprime array based on decoupled atomic norm minimization[J]. IEEE Access, 2020, 8: 57786–57795. doi: 10.1109/ACCESS.2020.2982413 [23] HUA Yingbo. A pencil-MUSIC algorithm for finding two-dimensional angles and polarizations using crossed dipoles[J]. IEEE Transactions on Antennas and Propagation, 1993, 41(3): 370–376. doi: 10.1109/8.233122 -





 下载:
下载:


 下载:
下载:
