Laws and Mechanism of Dual-frequency Insensitive Effect of Blocking Interference
-
摘要: 该文通过引入幂级数展开式的5阶项对双频干扰下系统非线性失真进行分析,揭示了阻塞干扰产生双频钝感现象的本质原因,并进行了试验验证。理论分析与试验结果表明,当干扰信号强度较弱、系统非线性失真程度较低时,可用精确到3阶项的幂级数展开式描述其传递函数,此时受试装备对双频干扰场强的有效值敏感;随着干扰信号增强,系统非线性失真程度上升,幂级数展开式中的5阶项不可忽略,受试装备对双频干扰出现阻塞效应减弱现象;阻塞程度越高,双频阻塞减弱现象越严重。Abstract: By introducing the 5th-order term of power series expansion, the nonlinear distortion of the system under dual -frequency interference is analyzed, and the essential reason of dual-frequency insensitive effect caused by blocking interference is revealed, which is verified by experiments. Theoretical analysis and experimental results show that when the interference signal strength is weak and the nonlinear distortion of the system is low, the transfer function can be described by the power series expansion accurate to the 3rd-order term, and the test equipment is sensitive to the effective value of the dual -frequency interference field strength; with the increase of the interference signal, the nonlinear distortion of the system increases, and the 5th-order term in the power series expansion cannot be ignored, and the higher the blocking degree is, the more serious the dual-frequency insensitive effect is.
-
表 1 以峰值电平压缩1.5 dB为敏感判据试验结果
Ei/Ei0 Δf1= 0 Hz 0.84 0.72 0.66 0.60 Δf2 =90 MHz 0.56 0.72 0.78 0.82 R 1.02 1.03 1.03 1.04 Δf1= –150 MHz 0.88 0.76 0.66 0.53 Δf2 =150 MHz 0.47 0.65 0.78 0.85 R 1.00 1.00 1.04 1.01 表 2 以峰值电平压缩6 dB为敏感判据试验结果
Ei/Ei0 Δf1= 0 Hz 1.09 0.87 0.77 0.68 Δf2 =90 MHz 0.72 0.77 0.83 0.90 R 1.71 1.35 1.29 1.27 Δf1= –150 MHz 0.89 0.80 0.70 0.62 Δf2 =150 MHz 0.66 0.80 0.85 0.89 R 1.24 1.28 1.21 1.18 表 3 以峰值电平压缩12 dB为敏感判据试验结果
Ei/Ei0 Δf1= 0 Hz 1.11 1.06 0.91 0.80 Δf2 =90 MHz 0.99 1.07 1.14 1.16 R 2.22 2.27 2.12 1.98 Δf1= –150 MHz 1.12 0.84 0.70 0.65 Δf2 =150 MHz 0.71 0.91 1.05 1.08 R 1.77 1.52 1.59 1.59 表 4 单频临界干扰场强与选择系数比
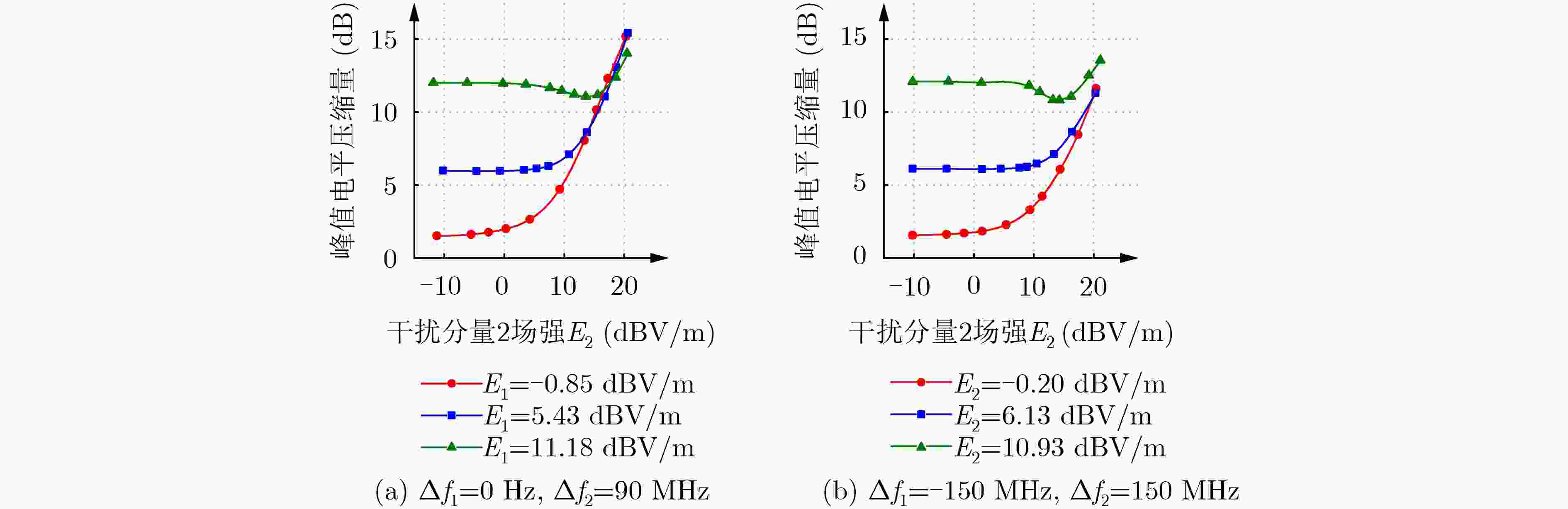
峰值电平压缩量 单频临界干扰场强(dBV/m) A1/A2均值 6 dB 12 dB Δf1=0 Hz 5.43 11.18 1.90 Δf2=90 MHz 11.10 16.70 Δf1=–150 MHz 6.13 10.93 2.60 Δf2=150 MHz 14.26 19.99 表 5 频偏0 Hz, 90 MHz双频干扰试验结果
Δf1=0 Hz Δf2=90 MHz 有效电平差
(V)峰值电平
压缩量(dB)干扰场强
(dBV/m)5.43 / / 5.99 / 11.10 / 5.98 –4.20 10.56 2.20 5.24 –2.20 10.24 1.78 5.07 0.60 9.34 0.90 4.78 4.30 4.81 1.38 4.99 干扰场强
(dBV/m)11.18 / / 12.01 / 16.70 / 11.96 3.80 15.84 3.25 10.15 5.80 15.23 2.07 9.58 6.80 14.74 1.30 9.30 8.80 12.94 0.80 9.13 表 6 频偏–150MHz, 150 MHz双频干扰试验结果
Δf1=–150 MHz Δf2=150 MHz 有效电平差
(V)峰值电平
压缩量(dB)干扰场强
(dBV/m)6.13 / / 6.03 / 14.26 / 6.00 –2.20 13.71 2.79 5.21 0.80 12.85 1.49 5.04 2.30 11.99 0.52 4.93 5.30 5.95 2.90 5.08 干扰场强
(dBV/m)10.93 / / 11.96 / 19.99 / 11.95 3.80 19.06 5.01 9.90 5.80 18.40 3.39 9.74 8.40 16.44 0.19 9.56 10.00 12.83 2.94 9.71 -
[1] IEC. CISPR 16–2–2 Specification for radio disturbance and immunity measuring apparatus and methods-Part 2–2: Methods of measurement of disturbances and immunity-Measurement of disturbance power[S]. IEC, 2010. [2] 中国人民解放军总装备部. GJB 151B-2013 军用设备和分系统电磁发射和敏感度要求与测量[S]. 2013.PLA General Equipment Department. GJB 151B-2013 Electromagnetic emission and susceptibility requirements and measurements for military equipment and subsystems[S]. 2013. [3] IEC. IEC/TS 61000-1-2 Electromagnetic compatibility (EMC)-Part 1–2: General- Methodology for the achievement of functional safety of electrical and electronic systems including equipment with regard to electromagnetic phenomena[S]. IEC, 2016. [4] ARMSTRONG K. How to manage risks with regard to electromagnetic disturbances[C]. 2016 IEEE International Symposium on Electromagnetic Compatibility, Ottawa, Canada, 2016. doi: 10.1109/ISEMC.2016.7571610. [5] ARMSTRONG K, PISSOORT D, DEGRAEVE A, et al. Risk management of electromagnetic disturbances[C]. 2018 IEEE International Symposium on Electromagnetic Compatibility and 2018 IEEE Asia-Pacific Symposium on Electromagnetic Compatibility, Suntec City, Singapore, 2018: 193–198. doi: 10.1109/ISEMC.2018.8393765. [6] RADASKY W A and ARMSTRONG K. Non-standardized immunity test techniques to help manage risks caused by EM disturbances[C]. 2016 IEEE International Symposium on Electromagnetic Compatibility, Ottawa, Canada, 2016: 84–89. doi: 10.1109/ISEMC.2016.7571614. [7] 王雅平, 魏光辉, 潘晓东, 等. 通信电台带外双频干扰预测模型与试验[J]. 电子学报, 2019, 47(4): 826–831. doi: 10.3969/j.issn.0372-2112.2019.04.009WANG Yaping, WEI Guanghui, PAN Xiaodong, et al. Out-of-band dual frequency jamming prediction model and experiment for communication stations[J]. Acta Electronica Sinica, 2019, 47(4): 826–831. doi: 10.3969/j.issn.0372-2112.2019.04.009 [8] 李伟, 魏光辉, 潘晓东, 等. 复杂电磁环境下通信装备干扰预测方法[J]. 电子与信息学报, 2017, 39(11): 2782–2789. doi: 10.11999/JEIT170107LI Wei, WEI Guanghui, PAN Xiaodong, et al. Interference prediction method of communication equipment under complex electromagnetic environment[J]. Journal of Electronics &Information Technology, 2017, 39(11): 2782–2789. doi: 10.11999/JEIT170107 [9] 王雅平, 魏光辉, 李伟, 等. 接收机带内双频阻塞干扰机理建模与验证[J]. 北京理工大学学报, 2018, 38(7): 709–814. doi: 10.15918/j.tbit1001-0645.2018.07.008WANG Yaping, WEI Guanghui, LI Wei, et al. Mechanism modeling and verification of receiver with in-band dual-frequency blocking jamming[J]. Transactions of Beijing Institute of Technology, 2018, 38(7): 709–814. doi: 10.15918/j.tbit1001-0645.2018.07.008 [10] LI Wei, WEI Guanghui, PAN Xiaodong, et al. Electromagnetic compatibility prediction method under the multifrequency in-band interference environment[J]. IEEE Transactions on Electromagnetic Compatibility, 2018, 60(2): 520–528. doi: 10.1109/TEMC.2017.2720961 [11] ZHAO Kai, WEI Guanghui, WANG Yaping, et al. Prediction model of in-band blocking interference under the electromagnetic radiation of dual-frequency continuous wave[J]. International Journal of Antennas and Propagation, 2020, 2020: 7651389. doi: 10.1155/2020/7651389 [12] DOMINO W, VAKILIAN N, and AGAHI D. Polynomial model of blocker effects on LNA/mixer devices[J]. Applied Microwave & Wireless, 2001, 13(6): 30–44. [13] 赵凯, 魏光辉, 潘晓东, 等. 单频电磁辐射对雷达的干扰规律[J]. 系统工程与电子技术, 2021, 43(2): 363–368. doi: 10.12305/j.issn.1001-506X.2021.02.10ZHAO Kai, WEI Guanghui, PAN Xiaodong, et al. Interference laws of single frequency electromagnetic radiation to radar[J]. Systems Engineering and Electronics, 2021, 43(2): 363–368. doi: 10.12305/j.issn.1001-506X.2021.02.10 [14] 魏光辉, 潘晓东, 万浩江. 装备电磁辐射效应规律与作用机理[M]. 北京: 国防工业出版社, 2018: 87–106.WEI Guanghui, PAN Xiaodong, and WAN Haojiang. Feature and Mechanism of Electromagnetic Radiation Effects for Equipment[M]. Beijing: Nation Defense Industry Press, 2018: 87–106. [15] AL-KANAN H, YANG Xianzhen, and LI Fu. Improved estimation for Saleh model and predistortion of power amplifiers using 1-dB compression point[J]. The Journal of Engineering, 2020, 2020(1): 13–18. doi: 10.1049/joe.2019.0973 [16] 魏光辉, 王雅平, 潘晓东, 等. 带外电磁辐射三阶互调阻塞干扰预测方法及终端设备[P]. 中国专利, 108833039, 2020.WEI Guanghui, WANG Yaping, PAN Xiaodong, et al. Out-of-band electromagnetic radiation third-order intermodulation barrage jamming prediction method and terminal equipment[P]. China Patent, 108833039, 2020. [17] 魏光辉, 赵凯, 任仕召. 通信电台电磁辐射2阶互调低频阻塞效应与作用机理[J]. 电子与信息学报, 2020, 42(8): 2059–2064. doi: 10.11999/JEIT190574WEI Guanghui, ZHAO Kai, and REN Shizhao. Second-order intermodulation low frequency blocking effect and mechanism for communication radio under electromagnetic radiation[J]. Journal of Electronics &Information Technology, 2020, 42(8): 2059–2064. doi: 10.11999/JEIT190574 -





 下载:
下载:


 下载:
下载:
