基于V-结构&amp;对数似然函数定向与禁忌爬山的贝叶斯网络结构算法

刘浩然; 王念太; 王毅; 张力悦; 苏昭玉; 刘文; 赵旭丹

doi:10.11999/JEIT210032

基于V-结构&对数似然函数定向与禁忌爬山的贝叶斯网络结构算法

doi: 10.11999/JEIT210032

刘浩然^{1, 2, ,},
王念太^{1, 2},
王毅^{1, 2},
张力悦^{1, 2},
苏昭玉^{1, 2},
刘文³,
赵旭丹³

1.
燕山大学信息科学与工程学院秦皇岛 066004
2.
河北省特种光纤与光纤传感重点实验室秦皇岛 066004
3.
北京市机电研究院北京 100027

基金项目: 国家重点研发计划(2019YFB1707301)，河北省人才工程培养资助项目(A201903005)

详细信息

作者简介:
刘浩然：男，1980年生，教授，博士生导师，研究方向为无线传感器网络、工业故障检测及预测

王念太：男，1996年生，硕士生，研究方向为贝叶斯网络、工业故障检测及预测

王毅：男，1996年生，硕士生，研究方向为贝叶斯网络、工业故障检测及预测

张力悦：男，1994年生，博士生，研究方向为贝叶斯网络、工业故障检测及预测

苏昭玉：女，1994年生，硕士生，研究方向为贝叶斯网络、工业故障检测及预测

刘文：女，1966年生，学士，研究方向为机床工艺参数感知与预测

赵旭丹：女，1981年生，硕士，研究方向为财务会计理论与方法

通讯作者:
刘浩然　liu.haoran@ysu.edu.cn

中图分类号: TP18
计量
- 文章访问数: 1293
- HTML全文浏览量: 620
- PDF下载量: 97
- 被引次数: 0
出版历程
- 收稿日期: 2021-01-11
- 修回日期: 2021-04-21
- 网络出版日期: 2021-05-07
- 刊出日期: 2021-11-23

Bayesian Network Structure Algorithm Based on V-structure & Log-Likelihood Orientation and Tabu Hill Climbing

Haoran LIU^{1, 2
, ,},
Niantai WANG^{1, 2},
Yi WANG^{1, 2},
Liyue ZHANG^{1, 2},
Zhaoyu SU^{1, 2},
Wen LIU³,
Xudan ZHAO³

1.
School of Information Science and Engineering, Yanshan University, Qinhuangdao 066004, China
2.
The Key Laboratory for Special Fiber and Fiber Sensor of Hebei Province, Yanshan University, Qinhuangdao 066004, China
3.
Beijing Institute of Mechanical and Electrical Engineering, Beijing 100027, China

Funds: The National Key R&D Program of China (2019YFB1707301), The Hebei Talent Engineering Training Support Project (A201903005)

摘要

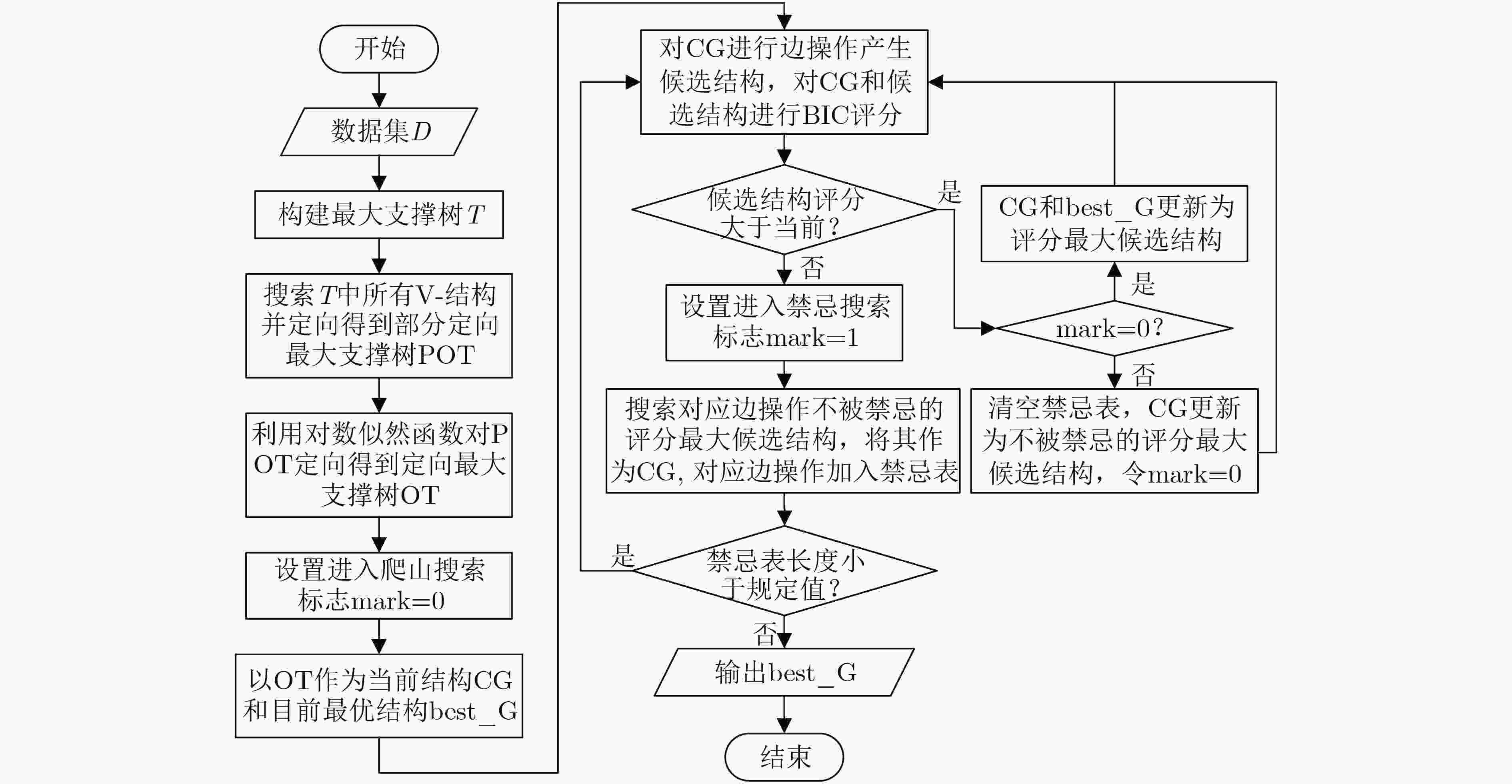
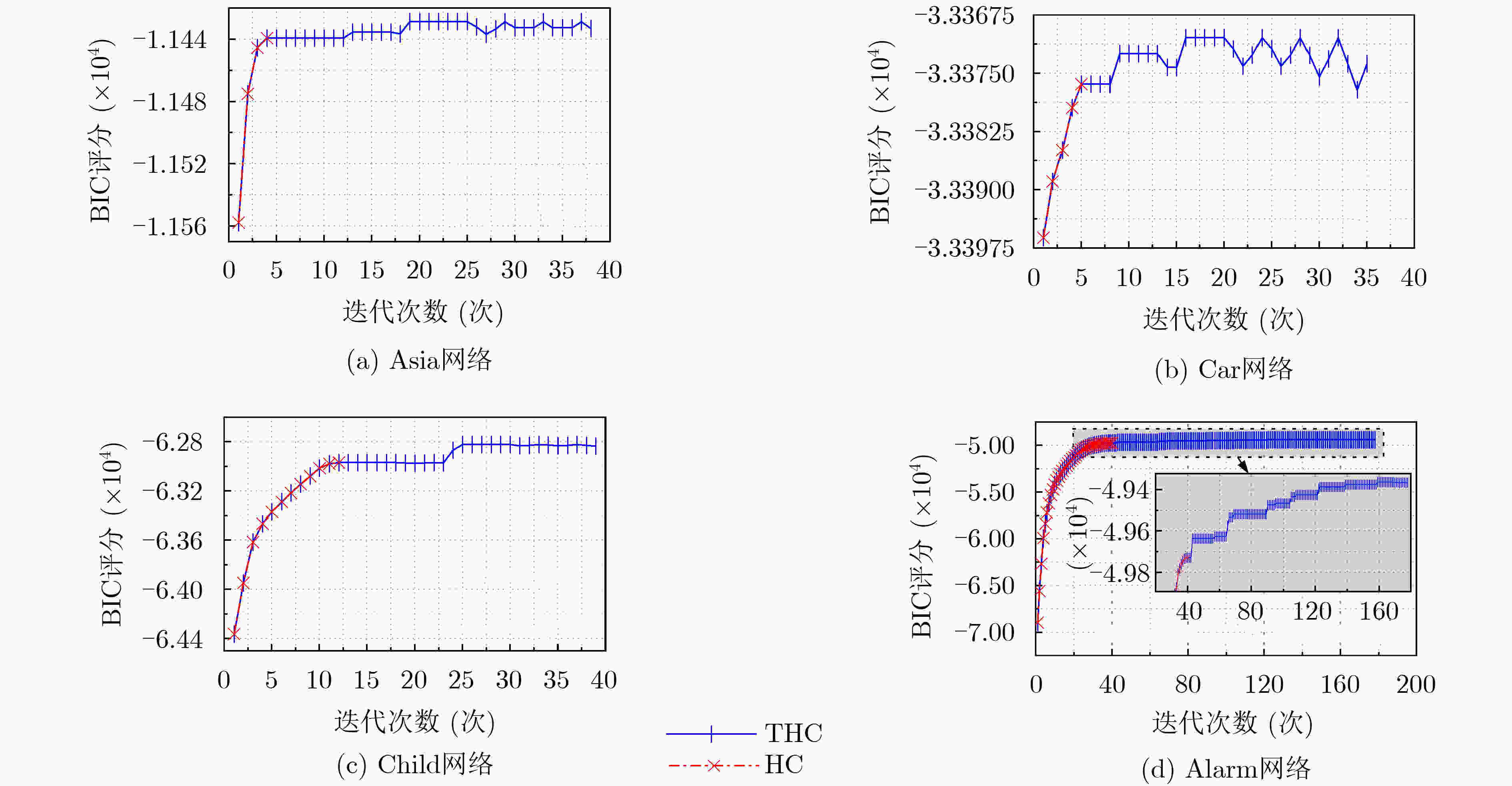
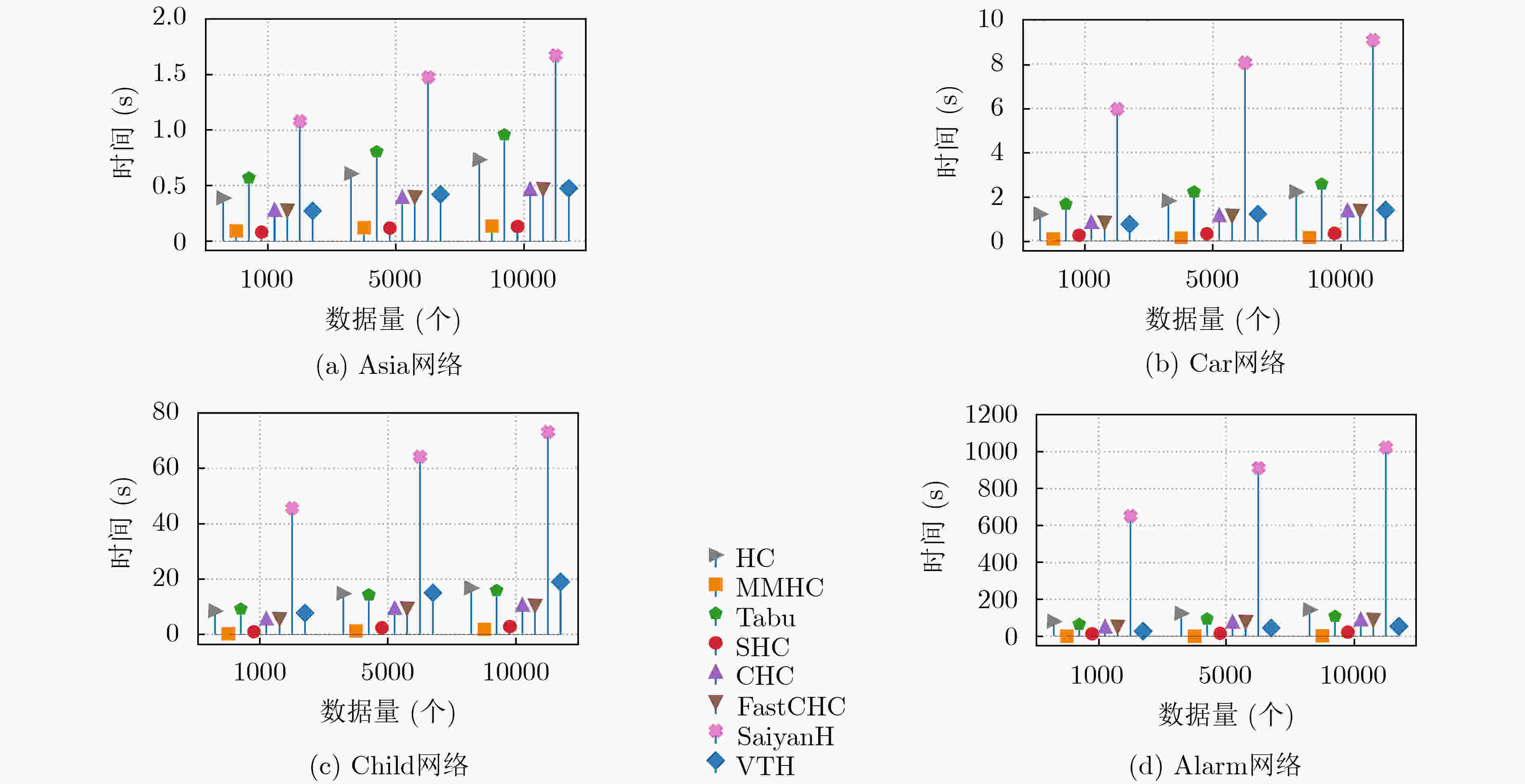
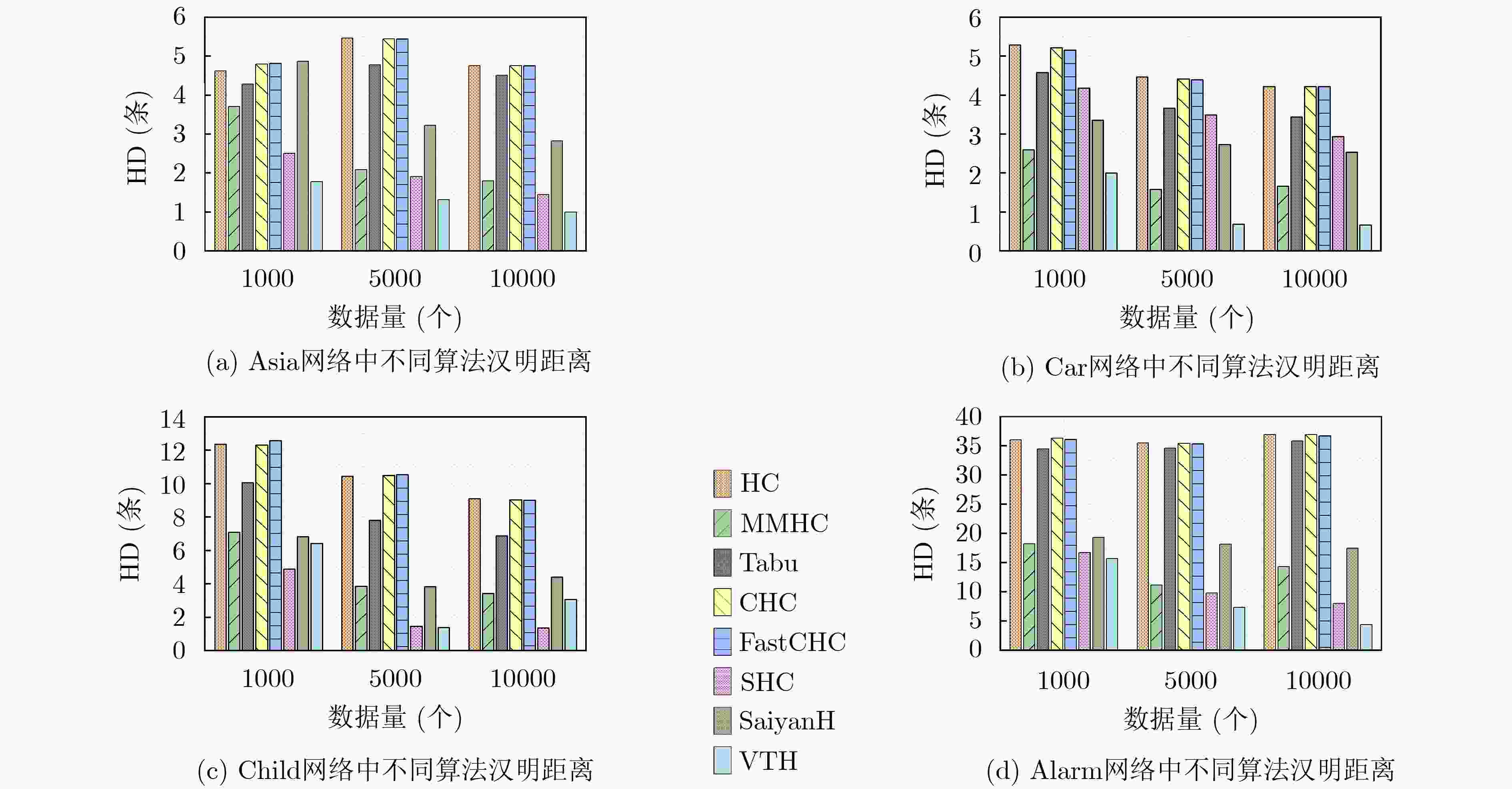
摘要: 针对爬山算法搜索空间过大和易陷入局部最优的问题，该文提出基于V-结构&对数似然函数定向与禁忌爬山的贝叶斯网络结构算法(VTH)。该算法利用定向最大支撑树约束搜索空间，在最大支撑树定向过程中，提出V-结构与对数似然函数(VLL)结合的定向策略；在评分搜索过程中，提出禁忌爬山(VTH)评分搜索策略，该策略将禁忌表清空机制与爬山搜索的局部择优准则结合，在提高全局寻优能力的同时也能保证搜索效率。该算法与其他算法在Asia, Car, Child和Alarm 4种标准网络中进行仿真实验，对比汉明距离、F1值、平衡评分函数(BSF)值、运行时间4个指标，验证了该算法的有效性。
- 贝叶斯网络结构 /
- 爬山算法 /
- 禁忌搜索 /
- 定向最大支撑树
Abstract: Hill climbing algorithm has too large search space and is easy to fall into local optimum. In this paper, a new Bayesian network structure algorithm based on V-structure & log-likelihood orientation and Tabu Hill (VTH) climbing is proposed. The algorithm limits the search space by using the oriented maximum weight spanning tree. In the process of maximum weight spanning tree orientation, the orientation strategy based on V-structure and Log-Likelihood (VLL) function is proposed. Tabu Hill Climbing (THC) scoring search strategy is established during the process of search, it combines the tabu list clearing mechanism with the local optimization criteria of hill climbing, the strategy not only ensures the search efficiency, but also improves the global optimization ability. By comparing Hamming distance, F1-value, Balanced Scoring Function(BSF) value and Time with other algorithms in Asia, Car, Child and Alarm standard networks, the effectiveness of the proposed algorithm is verified.
- Bayesian network structure /
- Hill climbing algorithm /
- Tabu search /
- Oriented maximum weight spanning tree

HTML全文

图 1 最大支撑树中3节点连接关系

下载: 全尺寸图片幻灯片

图 2 ep修改CG得到候选结构

下载: 全尺寸图片幻灯片

图 3 VTH算法流程图

下载: 全尺寸图片幻灯片

图 4 HC与THC在4种网络中寻优过程对比

下载: 全尺寸图片幻灯片

图 5 4个网络中不同算法运行时间结果

下载: 全尺寸图片幻灯片

图 6 4个网络中不同算法汉明距离结果

下载: 全尺寸图片幻灯片

表 1 4种网络中VLL策略和CRAE策略定向结果

网络	数据量	VLL策略			CRAE策略
网络	数据量	T	F	acc(%)	T	F	acc(%)
Asia	1000	5.56	0.58	90.58	3.58	2.56	58.33
	5000	6.02	0.47	92.81	3.62	2.87	55.82
	10000	6.27	0.47	93.07	3.71	3.02	55.12
Car	1000	7.93	0.96	89.25	5.87	3.02	66.00
	5000	8.18	0.82	90.86	6.00	2.98	66.83
	10000	8.11	0.89	90.12	6.00	3.00	66.67
Child	1000	13.78	4.98	73.46	14.31	4.44	76.30
	5000	13.93	5.07	73.33	14.20	4.80	74.74
	10000	13.98	5.02	73.57	14.18	4.82	74.62
Alarm	1000	33.49	0.44	98.69	23.40	10.53	68.96
	5000	34.02	0	100.00	22.84	11.18	67.15
	10000	34.00	0	100.00	22.69	11.31	66.73

下载: 导出CSV

表 2 对比算法介绍

算法	描述
HC算法	经典爬山算法
Tabu算法	利用禁忌表提高爬山全局寻优能力的禁忌搜索算法
MMHC算法	依赖分析与爬山算法结合的经典混合算法
CHC算法	通过动态限制提高爬山效率的高效算法
FastCHC算法	对CHC算法的改进算法
SHC算法	标准节点序定向最大支撑树与简化爬山结合的有效算法
SaiyanH算法	新近提出的爬山算法和禁忌搜索结合的混合算法

下载: 导出CSV

表 4 Car网络中不同算法F1值和BSF值结果

数据量	对比项	HC	MMHC	Tabu	SHC	CHC	FastCHC	SaiyanH	VTH
1000	F1	0.6383	0.8317	0.6962	0.7690	0.6456	0.6495	0.7852	0.8810
1000	BSF	0.6357	0.7589	0.6742	0.7686	0.6410	0.6430	0.7380	0.8203
5000	F1	0.7133	0.9042	0.7673	0.8133	0.7161	0.7179	0.8299	0.9609
5000	BSF	0.6989	0.8333	0.7345	0.8118	0.7006	0.7020	0.7785	0.8958
10000	F1	0.7346	0.8982	0.7844	0.8462	0.7346	0.7346	0.8443	0.9617
10000	BSF	0.7164	0.8277	0.7485	0.8426	0.7164	0.7164	0.7911	0.8919

下载: 导出CSV

表 5 Child网络中不同算法F1值和BSF值结果

数据量	对比项	HC	MMHC	Tabu	SHC	CHC	FastCHC	SaiyanH	VTH
1000	F1	0.7054	0.8367	0.7644	0.8930	0.7068	0.6999	0.8467	0.8554
1000	BSF	0.6193	0.7250	0.6649	0.7736	0.6209	0.6152	0.7308	0.7386
5000	F1	0.7666	0.9167	0.8291	0.9698	0.7654	0.7636	0.9187	0.9715
5000	BSF	0.7273	0.8422	0.7776	0.9014	0.7273	0.7251	0.8526	0.9061
10000	F1	0.8000	0.9267	0.8514	0.9717	0.8016	0.8021	0.9061	0.9366
10000	BSF	0.7607	0.8569	0.8006	0.9030	0.7621	0.7626	0.8466	0.8775

下载: 导出CSV

表 3 Asia网络中不同算法F1值和BSF值结果

数据量	对比项	HC	MMHC	Tabu	SHC	CHC	FastCHC	SaiyanH	VTH
1000	F1	0.6579	0.7450	0.6862	0.8369	0.6424	0.6401	0.6319	0.8788
1000	BSF	0.4964	0.5696	0.5192	0.6730	0.4841	0.4823	0.4782	0.6950
5000	F1	0.5900	0.8549	0.6481	0.8739	0.5923	0.5923	0.7687	0.9118
5000	BSF	0.4512	0.6812	0.4966	0.7137	0.4530	0.4530	0.5990	0.7325
10000	F1	0.6526	0.8748	0.6721	0.9046	0.6526	0.6526	0.7974	0.9335
10000	BSF	0.5069	0.7052	0.5226	0.7468	0.5069	0.5069	0.6300	0.7605

下载: 导出CSV

表 6 Alarm网络中不同算法F1值和BSF值结果

数据量	对比项	HC	MMHC	Tabu	SHC	CHC	FastCHC	SaiyanH	VTH
1000	F1	0.5128	0.7767	0.5369	0.7951	0.5068	0.5095	0.7616	0.8090
1000	BSF	0.5680	0.7644	0.5807	0.7457	0.5642	0.5658	0.7413	0.7545
5000	F1	0.5463	0.8690	0.5589	0.8866	0.5485	0.5485	0.7891	0.9165
5000	BSF	0.6413	0.8474	0.6485	0.8488	0.6425	0.6421	0.7955	0.8755
10000	F1	0.5313	0.8268	0.5484	0.9093	0.5308	0.5329	0.7972	0.9514
10000	BSF	0.6402	0.8183	0.6505	0.8856	0.6399	0.6381	0.8072	0.9174

下载: 导出CSV

参考文献(24)

[1]	李硕豪, 张军. 贝叶斯网络结构学习综述[J]. 计算机应用研究, 2015, 32(3): 641–646. doi: 10.3969/j.issn.1001-3695.2015.03.001 LI Shuohao and ZHANG Jun. Review of Bayesian networks structure learning[J]. Application Research of Computers, 2015, 32(3): 641–646. doi: 10.3969/j.issn.1001-3695.2015.03.001
[2]	ZHAO Xuan, PENG Benhong, ELAHI E, et al. Optimization of Chinese coal-fired power plants for cleaner production using Bayesian network[J]. Journal of Cleaner Production, 2020, 273: 122837. doi: 10.1016/j.jclepro.2020.122837
[3]	MCLACHLAN S, DUBE K, HITMAN G A, et al. Bayesian networks in healthcare: Distribution by medical condition[J]. Artificial Intelligence in Medicine, 2020, 107: 101912. doi: 10.1016/j.artmed.2020.101912
[4]	CARRIGER J F and BARRON M G. A Bayesian network approach to refining ecological risk assessments: Mercury and the Florida panther (Puma concolor coryi)[J]. Ecological Modelling, 2020, 418: 108911. doi: 10.1016/j.ecolmodel.2019.108911
[5]	ANDERSON B. Using Bayesian networks to perform reject inference[J]. Expert Systems with Applications, 2019, 137: 349–356. doi: 10.1016/j.eswa.2019.07.011
[6]	SCANAGATTA M, SALMERÓN A, and STELLA F. A survey on Bayesian network structure learning from data[J]. Progress in Artificial Intelligence, 2019, 8(4): 425–439. doi: 10.1007/s13748-019-00194-y
[7]	HECKERMAN D, GEIGER D, and CHICKERING D M. Learning Bayesian networks: The combination of knowledge and statistical data[J]. Machine Learning, 1995, 20(3): 197–243. doi: 10.1007/BF00994016
[8]	曹杰. 贝叶斯网络结构学习与应用研究[D].[博士论文], 中国科学技术大学, 2017. CAO Jie. Bayesian network structure learning and application[D].[Ph.D. dissertation], University of Science and Technology of China, 2017.
[9]	TSAMARDINOS I, BROWN L E, and ALIFERIS C F. The max-min hill-climbing Bayesian network structure learning algorithm[J]. Machine Learning, 2006, 65(1): 31–78. doi: 10.1007/s10994-006-6889-7
[10]	冀俊忠, 张鸿勋, 胡仁兵, 等. 基于禁忌搜索的贝叶斯网结构学习算法[J]. 北京工业大学学报, 2011, 37(8): 1274–1280. JI Junzhong, ZHANG Hongxun, HU Renbing, et al. A Tabu-search based Bayesian network structure learning algorithm[J]. Journal of Beijing University of Technology, 2011, 37(8): 1274–1280.
[11]	GÁMEZ J A, MATEO J L, and PUERTA J M. Learning Bayesian networks by hill climbing: Efficient methods based on progressive restriction of the neighborhood[J]. Data Mining and Knowledge Discovery, 2011, 22(1-2): 106–148. doi: 10.1007/s10618-010-0178-6
[12]	GÁMEZ J A, MATEO J L, and PUERTA J M. One iteration CHC algorithm for learning Bayesian networks: An effective and efficient algorithm for high dimensional problems[J]. Progress in Artificial Intelligence, 2012, 1(4): 329–346. doi: 10.1007/s13748-012-0033-7
[13]	ARIAS J, GÁMEZ J A, and PUERTA J M. Structural learning of Bayesian networks via constrained hill climbing algorithms: Adjusting trade-off between efficiency and accuracy[J]. International Journal of Intelligent Systems, 2015, 30(3): 292–325. doi: 10.1002/int.21701
[14]	刘浩然, 吕晓贺, 李轩, 等. 基于Bayesian改进算法的回转窑故障诊断模型研究[J]. 仪器仪表学报, 2015, 36(7): 1554–1561. doi: 10.3969/j.issn.0254-3087.2015.07.014 LIU Haoran, LÜ Xiaohe, LI Xuan, et al. A study on the fault diagnosis model of rotary kiln based on an improved algorithm of Bayesian[J]. Chinese Journal of Scientific Instrument, 2015, 36(7): 1554–1561. doi: 10.3969/j.issn.0254-3087.2015.07.014
[15]	刘彬, 刘永记, 刘浩然, 等. 基于改进遗传爬山算法的篦冷机熟料换热二次风温故障诊断[J]. 计量学报, 2018, 39(5): 651–658. doi: 10.3969/j.issn.1000-1158.2018.05.10 LIU Bin, LIU Yongji, LIU Haoran, et al. Fault diagnosis of secondary air temperature of grate cooler cement clinker heat transfer based on improved genetic hill climbing algorithm[J]. Acta Metrologica Sinica, 2018, 39(5): 651–658. doi: 10.3969/j.issn.1000-1158.2018.05.10
[16]	CONSTANTINOU A C. Learning Bayesian networks that enable full propagation of evidence[J]. IEEE Access, 2020, 8: 124845–124856. doi: 10.1109/ACCESS.2020.3006472
[17]	CHEN Guangjie and GE Zhiqiang. Robust Bayesian networks for low-quality data modeling and process monitoring applications[J]. Control Engineering Practice, 2020, 97: 104344. doi: 10.1016/j.conengprac.2020.104344
[18]	YANG Jing, GUO Xiaoxue, AN Ning, et al. Streaming feature-based causal structure learning algorithm with symmetrical uncertainty[J]. Information Sciences, 2018, 467: 708–724. doi: 10.1016/j.ins.2018.04.076
[19]	PRIM R C. Shortest connection networks and some generalizations[J]. The Bell System Technical Journal, 1957, 36(6): 1389–1401. doi: 10.1002/j.1538-7305.1957.tb01515.x
[20]	DAI Jingguo, REN Jia, and DU Wencai. Decomposition-based Bayesian network structure learning algorithm using local topology information[J]. Knowledge-Based Systems, 2020, 195: 105602. doi: 10.1016/j.knosys.2020.105602
[21]	BEHJATI S and BEIGY H. Improved K2 algorithm for Bayesian network structure learning[J]. Engineering Applications of Artificial Intelligence, 2020, 91: 103617. doi: 10.1016/j.engappai.2020.103617
[22]	ZHAO Jianjun and HO S S. Improving Bayesian network local structure learning via data-driven symmetry correction methods[J]. International Journal of Approximate Reasoning, 2019, 107: 101–121. doi: 10.1016/j.ijar.2019.02.004
[23]	CONSTANTINOU A C. The importance of temporal information in Bayesian network structure learning[J]. Expert Systems with Applications, 2021, 164: 113814. doi: 10.1016/j.eswa.2020.113814
[24]	JIANG Jinke, WANG Juyun, YU Hua, et al. Poison identification based on Bayesian network: A novel improvement on K2 algorithm via Markov Blanket[C]. The 4th International Conference on Advances in Swarm Intelligence, Harbin, China, 2013: 173–182.