基于正交基函数-编辑距离的低信噪比下磁异常信号相似性度量方法

邱景; 欧津东; 谢冬; 王铮; 杜杰卓

doi:10.11999/JEIT210029

基于正交基函数-编辑距离的低信噪比下磁异常信号相似性度量方法

doi: 10.11999/JEIT210029

重庆大学光电工程学院光电技术及系统教育部重点实验室重庆 400044

基金项目: 国家自然科学基金(51775070)，中央高校基本科研业务费专项基金(2019CDJGFGD002)

详细信息

作者简介:
邱景：男，1982年生，教授，研究方向为微弱磁场探测技术、可穿戴柔性传感技术、环境能量采集及自供电传感技术、雷达隐身技术

欧津东：男，1995年生，硕士生，研究方向为微弱磁场探测技术

谢冬：男，1995年生，硕士生，研究方向为微弱磁场探测技术

王铮：女，1996年生，硕士生，研究方向为微弱磁场探测技术

杜杰卓：男，1996年生，硕士生，研究方向为微弱磁场探测技术、可穿戴柔性传感技术

通讯作者:
邱景　jingqiu@cqu.edu.com

中图分类号: TN911.7; O441
计量
- 文章访问数: 1347
- HTML全文浏览量: 704
- PDF下载量: 102
- 被引次数: 0
出版历程
- 收稿日期: 2021-01-08
- 修回日期: 2021-06-24
- 网络出版日期: 2021-07-07
- 刊出日期: 2022-02-25

A Similarity Measurement Method for Magnetic Anomaly Signal under Low Signal-to-Noise Based on Orthogonal Basis Function–Edit Distance

Key Laboratory of Optoelectronic Technology and System of Ministry of Education, College of Optoelectronic Engineering, Chongqing University, Chongqing 400044, China

Funds: The National Natural Science Foundation of China (51775070), The Fundamental Research Funds for the Central Universities (2019CDJGFGD002)

摘要

摘要: 针对低信噪比下磁异常信号相似性难以度量的问题，该文提出基于正交基函数(OBF)分解和编辑距离法(EDR)相结合的OBF-EDR磁异常信号相似性度量方法。该方法通过对磁异常信号进行正交基函数分解得到离散基函数系数，根据背景噪声与基函数不相关的特性提高离散基函数系数信噪比，利用编辑距离法对离散基函数系数进行相似性计算从而间接实现对磁异常信号的相似性度量。仿真测试表明OBF-EDR方法相较于EDR算法可在更低信噪比情况下对磁异常信号进行相似性度量。
- 正交基函数 /
- 编辑距离 /
- 磁场曲线 /
- 相似性度量 /
- 低信噪比
Abstract: Considering the problem that the similarity of magnetic anomaly signals is difficult to measure under low signal-to-noise ratio, a similarity measurement method OBF-EDR based on the combination of Orthogonal Basis Function (OBF) decomposition and Edit Distance on Real sequence (EDR) is proposed. This method obtains discrete basis function coefficients by decomposing the magnetic anomaly signals with orthogonal basis functions method. The signal-to-Noise Ratio (SNR) of discrete basis function coefficients is improved due to the uncorrelated characteristics of background noise and basis functions. EDR is used to measure the discrete coefficients of the basis function so as to measure indirectly the similarity of the magnetic anomaly signals. The simulation test shows that the OBF-EDR method can measure the similarity of magnetic anomaly signals at a lower SNR than the EDR algorithm.
- Orthogonal Basis Function(OBF) /
- Edit distance /
- Magnetic signature waveform /
- Similarity measurement /
- Low Signal-to-Noise Rate (SNR)

HTML全文

图 1 磁异常探测模型图

下载: 全尺寸图片幻灯片

图 2 原始磁异常信号

下载: 全尺寸图片幻灯片

图 3 含噪磁异常信号

下载: 全尺寸图片幻灯片

图 4 X轴方向磁异常信号离散基函数系数

下载: 全尺寸图片幻灯片

图 5 Y轴方向磁异常信号离散基函数系数

下载: 全尺寸图片幻灯片

图 6 Z轴方向磁异常信号离散基函数系数

下载: 全尺寸图片幻灯片

图 7 序列A转换为序列B的编辑距离计算过程

下载: 全尺寸图片幻灯片

图 8 X轴方向磁异常测试信号

下载: 全尺寸图片幻灯片

图 9 Y 轴方向磁异常测试信号

下载: 全尺寸图片幻灯片

图 10 Z轴方向磁异常测试信号

下载: 全尺寸图片幻灯片

图 11 FAR随SNR变化情况

下载: 全尺寸图片幻灯片

图 12 FRR随SNR变化情况

下载: 全尺寸图片幻灯片

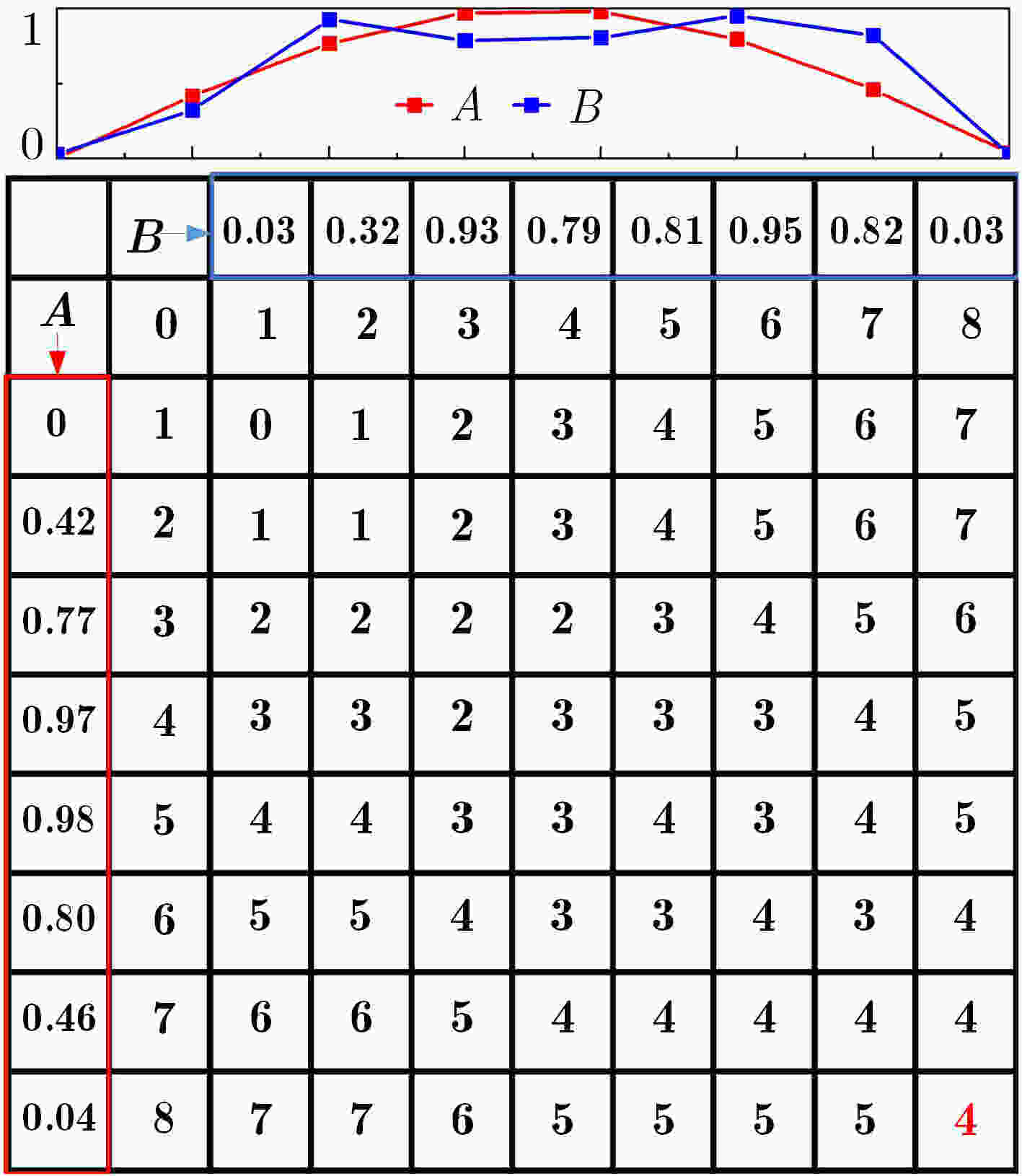
表 1 EDR算法伪代码

输入：两个实数序列A和B
输出：序列A与B的相似度
第1步：计算序列A,B的长度以及阈值e
L_A=LENGTH(A); L_B=LENGTH(B); e=0.1× (max(A)–min(A))
第2步：创建编辑距离矩阵E [L_A+1, L_B+1]并进行初始化
E [0,0]=0
for each row i from 1 to L_A do
E [i, 0] ← E [i–1, 0]+deleteCost(A [i], B [0])
for each column j from 1 to L_B do
E [0, j] ← E [0, j–1]+insertCost(A [0], B [j])
第3步：循环执行
for each row i from 1 to L_A do
for each column j from 1 to L_B do
E [i, j] ← min(E [i–1, j]+deleteCost(A [i], B [j]),
E [i, j–1]+insertCost(A [i], B [j]),
E [i–1, j–1]+substituteCost(A [i], B [j]))
end
end
第4步：返回1–E [L_A, L_B]/max(L_A, L_B)

下载: 导出CSV

表 2 OBF-EDR计算磁异常信号相似度结果

计算对象	${{S} }{ {\rm{\alpha} } _1}$	${W_1}$	${{S} }{ {\rm{\alpha} } _2}$	${W_2}$	${{S} }{ {\rm{\alpha} } _3}$	${W_3}$	${\rm{sLines}}$
${B_x}$和${{\rm{Br}}_x}$	1.000	0.700	0.768	0.145	0.816	0.155	0.938
${B_y}$和${{\rm{Br}}_y}$	1.000	0.718	0.794	0.138	0.829	0.143	0.946
${B_z}$和${{\rm{Br}}_z}$	0.961	0.782	0.724	0.086	0.754	0.132	0.913

下载: 导出CSV

表 3 EDR计算磁异常信号相似度结果

	计算对象
	${B_x}$和${\rm{B}}{{\rm{r}}_x}$	${B_y}$和${\rm{B}}{{\rm{r}}_y}$	${B_z}$和${\rm{B}}{{\rm{r}}_z}$
相似度	0.75	0.767	0.741

下载: 导出CSV

参考文献(22)

[1]	LAN Jinhui, XIANG Yong, WANG Liping, et al. Vehicle detection and classification by measuring and processing magnetic signal[J]. Measurement, 2011, 44(1): 174–180. doi: 10.1016/j.measurement.2010.09.044
[2]	李开明, 张群, 罗迎, 等. 地面车辆目标识别研究综述[J]. 电子学报, 2014, 42(3): 538–546. doi: 10.3969/j.issn.0372-2112.2014.03.018 LI Kaiming, ZHANG Qun, LUO Ying, et al. Review of ground vehicles recognition[J]. Acta Electronica Sinica, 2014, 42(3): 538–546. doi: 10.3969/j.issn.0372-2112.2014.03.018
[3]	林君, 刁庶, 张洋, 等. 地球物理矢量场磁测技术的研究进展[J]. 科学通报, 2017, 62(23): 2606–2618. doi: 10.1360/N972017-00010 LIN Jun, DIAO Shu, ZHANG Yang, et al. Research progress of geophysical vector magnetic field survey technology[J]. Chinese Science Bulletin, 2017, 62(23): 2606–2618. doi: 10.1360/N972017-00010
[4]	周家新, 陈建勇, 单志超, 等. 航空磁探中潜艇目标的联合估计检测方法研究[J]. 兵工学报, 2018, 39(5): 833–840. doi: 10.3969/j.issn.1000-1093.2018.05.001 ZHOU Jiaxin, CHEN Jianyong, SHAN Zhichao, et al. Research on joint estimation and detection of submarine target in airborne magnetic anomaly detection[J]. Acta Armamentarii, 2018, 39(5): 833–840. doi: 10.3969/j.issn.1000-1093.2018.05.001
[5]	ZHOU Jiaxin, CHEN Jianyong, and SHAN Zhichao. Spatial signature analysis of submarine magnetic anomaly at low altitude[J]. IEEE Transactions on Magnetics, 2017, 53(12): 6001107.
[6]	NAZLIBILEK S, KALENDER O, and EGE Y. Mine identification and classification by mobile sensor network using magnetic anomaly[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(3): 1028–1036. doi: 10.1109/TIM.2010.2060220
[7]	CHEN Xiao, KONG Xiaoying, XU Min, et al. Road vehicle detection and classification using magnetic field measurement[J]. IEEE Access, 2019, 7: 52622–52633. doi: 10.1109/ACCESS.2019.2908006
[8]	GAO Junqi, WANG Jiazeng, ZHANG Linjie, et al. Magnetic signature analysis for smart security system based on TMR magnetic sensor array[J]. IEEE Sensors Journal, 2019, 19(8): 3149–3155. doi: 10.1109/JSEN.2019.2891082
[9]	CHU Zhaoqiang, SHI Weiliang, SHI Huaduo, et al. A 1D magnetoelectric sensor array for magnetic sketching[J]. Advanced Materials Technologies, 2019, 4(3): 1800484. doi: 10.1002/admt.201800484
[10]	GINZBURG B, FRUMKIS L, and KAPLAN B Z. Processing of magnetic scalar gradiometer signals using orthonormalized functions[J]. Sensors and Actuators A: Physical, 2002, 102(1/2): 67–75.
[11]	SHEINKER A, SALOMONSKI N, GINZBURG B, et al. Magnetic anomaly detection using entropy filter[J]. Measurement Science and Technology, 2008, 19(4): 045205. doi: 10.1088/0957-0233/19/4/045205
[12]	SHEINKER A, GINZBURG B, SALOMONSKI N, et al. Magnetic anomaly detection using high-order crossing method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(4): 1095–1103. doi: 10.1109/TGRS.2011.2164086
[13]	SHEN Ying, WANG Jiazeng, SHI Jiedong, et al. Interpretation of signature waveform characteristics for magnetic anomaly detection using tunneling magnetoresistive sensor[J]. Journal of Magnetism and Magnetic Materials, 2019, 484: 164–171. doi: 10.1016/j.jmmm.2019.04.016
[14]	银鸿, 文轩, 杨生胜, 等. 基于磁异常检测的磁性运动目标识别方法研究[J]. 仪器仪表学报, 2018, 39(3): 258–264. YIN Hong, WEN Xuan, YNAG Shengsheng, et al. Research on the moving ferromagnetic object recognition method based on magnetic anomaly detection[J]. Chinese Journal of Scientific Instrument, 2018, 39(3): 258–264.
[15]	NAZLIBILEK S, EGE Y, KALENDER O, et al. Identification of materials with magnetic characteristics by neural networks[J]. Measurement, 2012, 45(4): 734–744. doi: 10.1016/j.measurement.2011.12.017
[16]	WANG Jiazeng, SHEN Ying, ZHAO Rui, et al. Estimation of dipole magnetic moment orientation based on magnetic signature waveform analysis by a magnetic sensor[J]. Journal of Magnetism and Magnetic Materials, 2020, 505: 166761. doi: 10.1016/j.jmmm.2020.166761
[17]	周星星, 吉根林, 张书亮. 时空轨迹相似性度量方法综述[J]. 地理信息世界, 2018, 25(4): 11–18. doi: 10.3969/j.issn.1672-1586.2018.04.003 ZHOU Xingxing, JI Genlin, and ZHANG Shuliang. Overview of the similarity measurement methods for spatial-temporal trajectory[J]. Geomatics World, 2018, 25(4): 11–18. doi: 10.3969/j.issn.1672-1586.2018.04.003
[18]	KEOGH E J and PAZZANI M J. Scaling up dynamic time warping for datamining applications[C]. The 6th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Boston, USA, 2000: 285–289.
[19]	CHEN Lei, ÖZSU M T, and ORIA V. Robust and fast similarity search for moving object trajectories[C]. 2005 ACM SIGMOD International Conference on Management of Data, Baltimore, USA, 2005: 491–502.
[20]	WAGNER R A and FISCHER M J. The string-to-string correction problem[J]. Journal of the ACM, 1974, 21(1): 168–173. doi: 10.1145/321796.321811
[21]	黄朝, 许鑫, 刘敦歌, 等. 基于多传感器的微弱磁异常信号提取方法研究[J]. 电子测量技术, 2015, 38(10): 91–95. doi: 10.3969/j.issn.1002-7300.2015.10.018 HUANG Chao, XU Xin, LIU Dunge, et al. Extraction method of weak magnetic anomaly signal based on multi-sensor[J]. Electronic Measurement Technology, 2015, 38(10): 91–95. doi: 10.3969/j.issn.1002-7300.2015.10.018
[22]	贺王鹏, 胡洁, 陈彬强, 等. 基于可调品质因子小波和簇稀疏增强的磁异常信号特征提取研究[J]. 航天器环境工程, 2020, 37(4): 355–360. doi: 10.12126/see.2020.04.007 HE Wangpeng, HU Jie, CHEN Binqiang, et al. Feature extraction of abnomal magnetic signals using tunable Q-factor wavelet transform and overlapping group shrinkage algorithm[J]. Spacecraft Environment Engineering, 2020, 37(4): 355–360. doi: 10.12126/see.2020.04.007