An Image Encryption Algorithm Based on Filling Curve and Adjacent Pixel Bit Scrambling
-
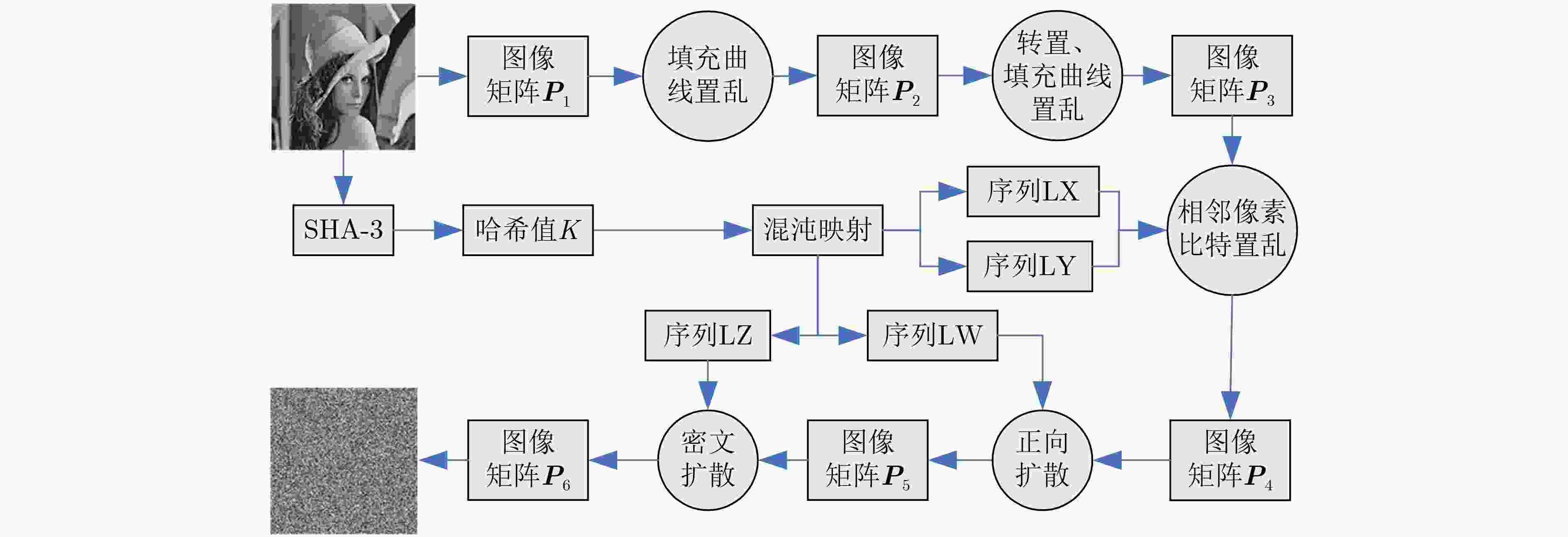
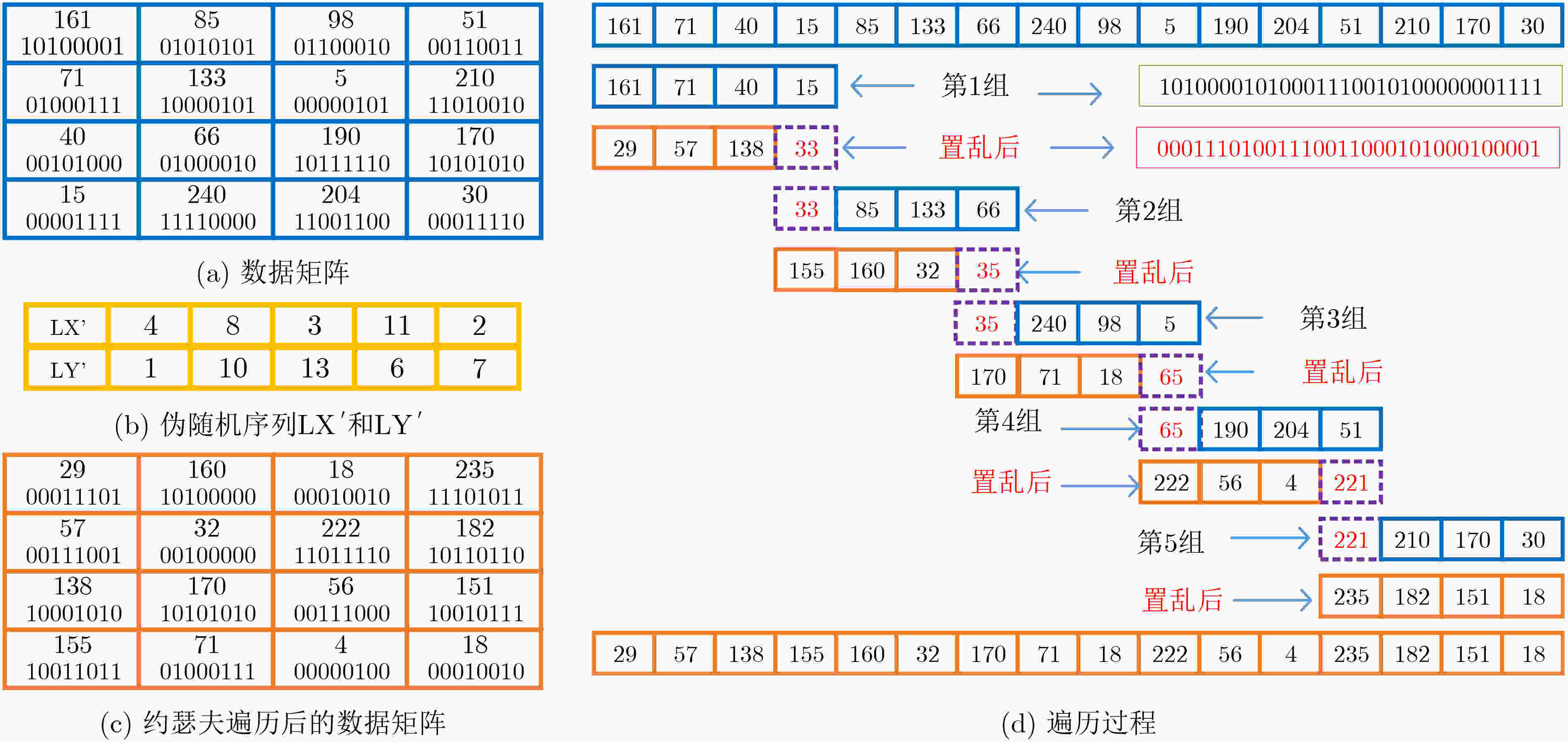
摘要: 为提高图像传输安全性,该文提出一种基于填充曲线和相邻像素比特置乱的加密算法。首先,设计一种新的填充曲线用于图像像素的全局置乱。其次,将混沌序列作为约瑟夫遍历的起点和步长,利用改进的约瑟夫遍历方法对相邻像素进行比特级置乱。像素级和比特级的双重置换,打破了图像像素间的高度相关性。最后,通过双向密文反馈,进一步提高方法的安全性。此外,设计了一种与明文图像关联的自适应密钥生成方法,以克服选择/已知明文攻击。并从密钥空间、密钥灵敏度、信息熵和相关性等性能指标对该方案进行了分析,结果表明,该算法具有良好的性能和足够的安全性。Abstract: To improve the security of image transmission, an encryption algorithm based on filling curve and adjacent pixel bit scrambling is proposed. Firstly, a new filling curve is designed and used to scramble image pixels globally. Secondly, the chaotic sequences are taken as the starting point and step length of Josephus traversal, and the adjacent pixels are bit scrambled by the improved Josephus traversal method. Through double scrambling, the high correlation between pixels of the plain image is broken. Finally, the security of the method is further improved by two-way ciphertext feedback. In addition, an adaptive key generation method associated with the plain image is designed to overcome the chosen/known-plaintext attack. The proposed scheme is analyzed from the aspects of key-space, key sensitivity, information entropy and correlations. The results show that this algorithm has good performance and sufficient security.
-
Key words:
- Image encryption /
- Space filling curve /
- Josephus traversal /
- Bit scrambling /
- Adjacent pixels
-
表 1 不同图像的密文图像的χ2分布统计
Lena Baboon Boat Elaine Pepper 明文 39851 79057 100853 36282 31629 密文 229.73 259.85 241.48 274.92 275.15 表 2 明文图像和密文图像各方向的相关系数
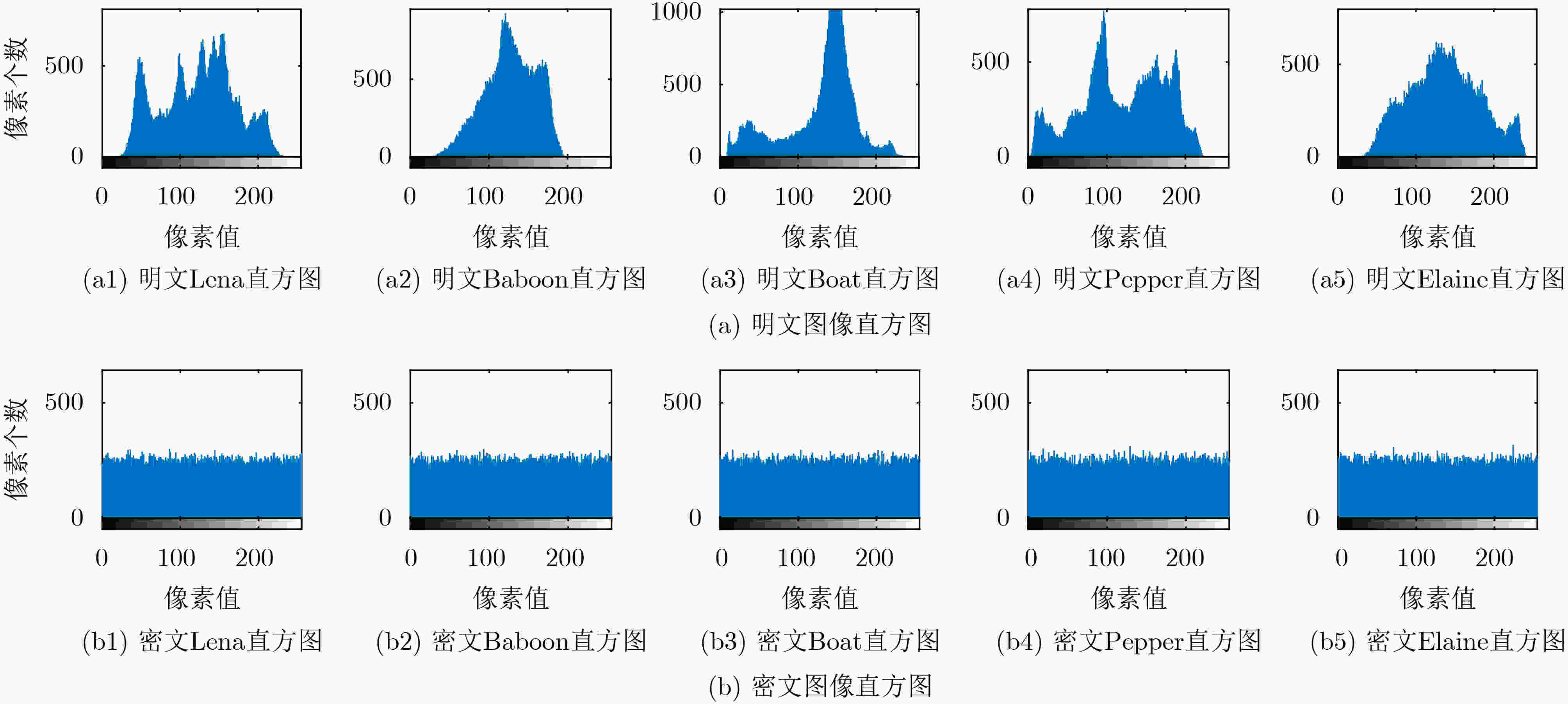
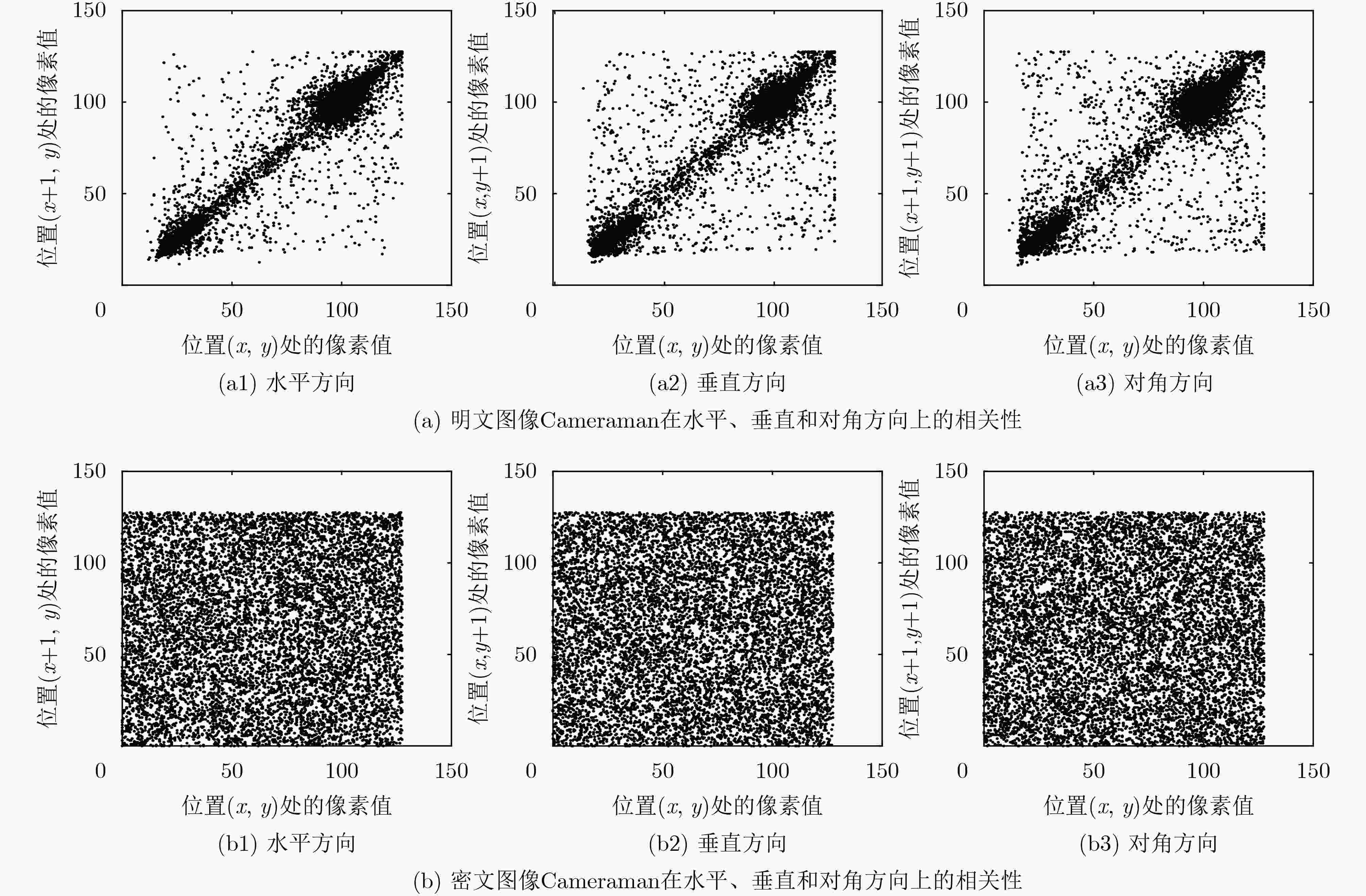
图像 明文 密文 水平 垂直 对角 水平 垂直 对角 Lena 0.9654 0.9309 0.9052 0.001299 –0.002880 –0.007894 Baboon 0.8302 0.8777 0.7883 0.003136 –0.001246 0.008514 Boat 0.9457 0.9277 0.8895 0.001249 –0.000359 –0.001481 Elaine 0.9769 0.9717 0.9506 –0.009156 0.001412 0.004994 Pepper 0.9695 0.9652 0.9376 –0.002798 –0.009152 –0.000651 表 3 不同图像的信息熵和局部信息熵
明文 密文 局部信息熵 Lena 7.4532 7.9975 7.9004 Baboon 7.0092 7.9971 7.9026 Boat 7.1572 7.9974 7.9040 Elaine 7.4874 7.9970 7.9030 Pepper 7.5797 7.9973 7.9029 表 4 明文图像发生微小改变时,对应密文图像间的NPCR和UACI的值(%)
Lena Baboon Boat Elaine Pepper NPCR 99.6750 99.6262 99.5789 99.6094 99.6063 UACI 33.4577 33.2147 33.2642 33.5752 33.3906 表 5 对于大小为256×256的Lena,本方案与其他方法的对比结果
方法 信息熵 NPCR (%) UACI (%) 相关系数 水平 垂直 对角 本文方法 7.9975 99.6750 33.4577 0.0013 –0.0029 –0.0079 文献[8] 7.9970 99.6100 33.4600 0.0022 0.0013 0.0008 文献[10] 7.9974 99.6114 33.4636 –0.0223 –0.0084 –0.0086 文献[11] 7.9969 – – –0.0004 0.0051 –0.0004 文献[12] 7.9976 99.4100 33.5700 0.0030 –0.0024 –0.0034 文献[13] 7.9972 99.6200 33.4000 –0.0015 –0.0032 0.0008 文献[17] 7.9971 99.5986 33.4561 –0.0029 –0.0017 0.0004 文献[20] 7.9967 99.6100 33.4600 0.0068 –0.0054 0.0010 -
[1] KAUR M and KUMAR V. A comprehensive review on image encryption techniques[J]. Archives of Computational Methods in Engineering, 2020, 27(1): 15–43. doi: 10.1007/s11831-018-9298-8 [2] 李付鹏, 刘敬彪, 王光义, 等. 基于混沌集的图像加密算法[J]. 电子与信息学报, 2020, 42(4): 981–987. doi: 10.11999/JEIT190344LI Fupeng, LIU Jingbiao, WANG Guangyi, et al. An image encryption algorithm based on chaos set[J]. Journal of Electronics &Information Technology, 2020, 42(4): 981–987. doi: 10.11999/JEIT190344 [3] FRIDRICH J. Symmetric ciphers based on two-dimensional chaotic maps[J]. International Journal of Bifurcation and Chaos, 1998, 8(6): 1259–1284. doi: 10.1142/S021812749800098X [4] LI Chunhu, LUO Guangchun, QIN Ke, et al. An image encryption scheme based on chaotic tent map[J]. Nonlinear Dynamics, 2017, 87(1): 127–133. doi: 10.1007/s11071-016-3030-8 [5] SOLAK E, ÇOKAL C, YILDIZ O T, et al. Cryptanalysis of fridrich's chaotic image encryption[J]. International Journal of Bifurcation and Chaos, 2010, 20(5): 1405–1413. doi: 10.1142/S0218127410026563 [6] RHOUMA R, SOLAK E, and BELGHITH S. Cryptanalysis of a new substitution-diffusion based image cipher[J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15(7): 1887–1892. doi: 10.1016/j.cnsns.2009.07.007 [7] HUA Zhongyun and ZHOU Yicong. Image encryption using 2D logistic-adjusted-sine map[J]. Information Sciences, 2016, 339: 237–253. doi: 10.1016/j.ins.2016.01.017 [8] CHEN Chen, SUN Kehui, and HE Shaobo. An improved image encryption algorithm with finite computing precision[J]. Signal Processing, 2020, 168: 107340. doi: 10.1016/j.sigpro.2019.107340 [9] FLORES-VERGARA A, INZUNZA-GONZALEZ E, GARCIA-GUERRERO E E, et al. Implementing a chaotic cryptosystem by performing parallel computing on embedded systems with multiprocessors[J]. Entropy, 2019, 21(3): 268. doi: 10.3390/e21030268 [10] ZHANG Yong. The fast image encryption algorithm based on lifting scheme and chaos[J]. Information Sciences, 2020, 520: 177–194. doi: 10.1016/j.ins.2020.02.012 [11] 廖春成, 周小平, 廖春龙, 等. 像素位置与比特双重置乱的混沌图像加密算法[J]. 中国科技论文, 2014, 9(1): 112–116. doi: 10.3969/j.issn.2095-2783.2014.01.022LIAO Chuncheng, ZHOU Xiaoping, LIAO Chunlong, et al. Chaotic image encryption algorithm based on dual scrambling of pixel position and bit[J]. China Sciencepaper, 2014, 9(1): 112–116. doi: 10.3969/j.issn.2095-2783.2014.01.022 [12] LIU Wenhao, SUN Kehui, and ZHU Congxu. A fast image encryption algorithm based on chaotic map[J]. Optics and Lasers in Engineering, 2016, 84: 26–36. doi: 10.1016/j.optlaseng.2016.03.019 [13] LI Yueping, WANG Chunhua, and CHEN Hua. A hyper-chaos-based image encryption algorithm using pixel-level permutation and bit-level permutation[J]. Optics and Lasers in Engineering, 2017, 90: 238–246. doi: 10.1016/j.optlaseng.2016.10.020 [14] SHAHNA K U and MOHAMED A. A novel image encryption scheme using both pixel level and bit level permutation with chaotic map[J]. Applied Soft Computing, 2020, 90: 106162. doi: 10.1016/j.asoc.2020.106162 [15] KANDAR S, CHAUDHURI D, BHATTACHARJEE A, et al. Image encryption using sequence generated by cyclic group[J]. Journal of Information Security and Applications, 2019, 44: 117–129. doi: 10.1016/j.jisa.2018.12.003 [16] MOZAFFARI S. Parallel image encryption with bitplane decomposition and genetic algorithm[J]. Multimedia Tools and Applications, 2018, 77(19): 25799–25819. doi: 10.1007/s11042-018-5817-8 [17] WANG Xingyuan, ZHU Xiaoqiang, and ZHANG Yingqian. An image encryption algorithm based on Josephus traversing and mixed chaotic map[J]. IEEE Access, 2018, 6: 23733–23746. doi: 10.1109/ACCESS.2018.2805847 [18] YANG Gelan, JIN Huixia, and Bai Na. Image encryption using the chaotic Josephus matrix[J]. Mathematical Problems in Engineering, 2014, 2014: 632060. doi: 10.1155/2014/632060 [19] CHAI Xiuli, GAN Zhihua, YANG Kang, et al. An image encryption algorithm based on the memristive hyperchaotic system, cellular automata and DNA sequence operations[J]. Signal Processing:Image Communication, 2017, 52: 6–19. doi: 10.1016/j.image.2016.12.007 [20] SUN Shuliang. A novel hyperchaotic image encryption scheme based on DNA encoding, pixel-level scrambling and bit-level scrambling[J]. IEEE Photonics Journal, 2018, 10(2): 7201714. doi: 10.1109/JPHOT.2018.2817550 [21] QI Guoyuan, VAN WYK M A, VAN WYK B J, et al. A new hyperchaotic system and its circuit implementation[J]. Chaos, Solitons & Fractals, 2009, 40(5): 2544–2549. doi: 10.1016/j.chaos.2007.10.053 [22] AQEEL-UR-REHMAN, LIAO Xiaofeng, KULSOOM A, et al. A modified (Dual) fusion technique for image encryption using SHA-256 hash and multiple chaotic maps[J]. Multimedia Tools and Applications, 2016, 75(18): 11241–11266. doi: 10.1007/s11042-015-2851-7 [23] 林土胜, 徐亚国. 信息加密的混沌流密码受参数变化影响的实验研究[J]. 中山大学学报:自然科学版, 2004, 43(S2): 101–104. doi: 10.3321/j.issn:0529-6579.2004.z2.026LIN Tusheng and XU Yaguo. Experimental study of different parameters on chaotic stream ciphers for information encryption[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2004, 43(S2): 101–104. doi: 10.3321/j.issn:0529-6579.2004.z2.026 -






 下载:
下载:







 下载:
下载:
