A Fast and Efficient FPGA-based Level Set Hardware Accelerator for Image Segmentation
-
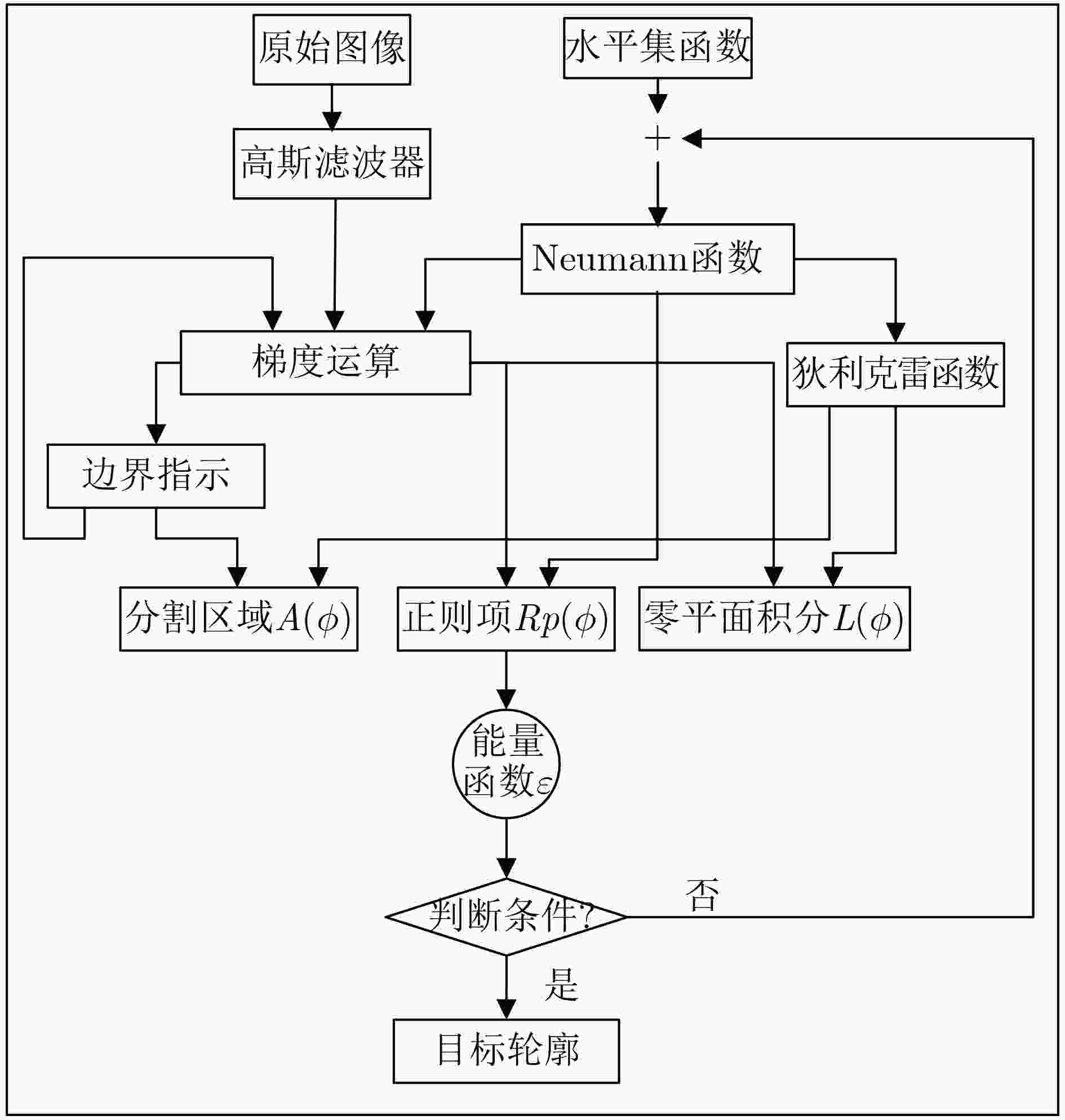
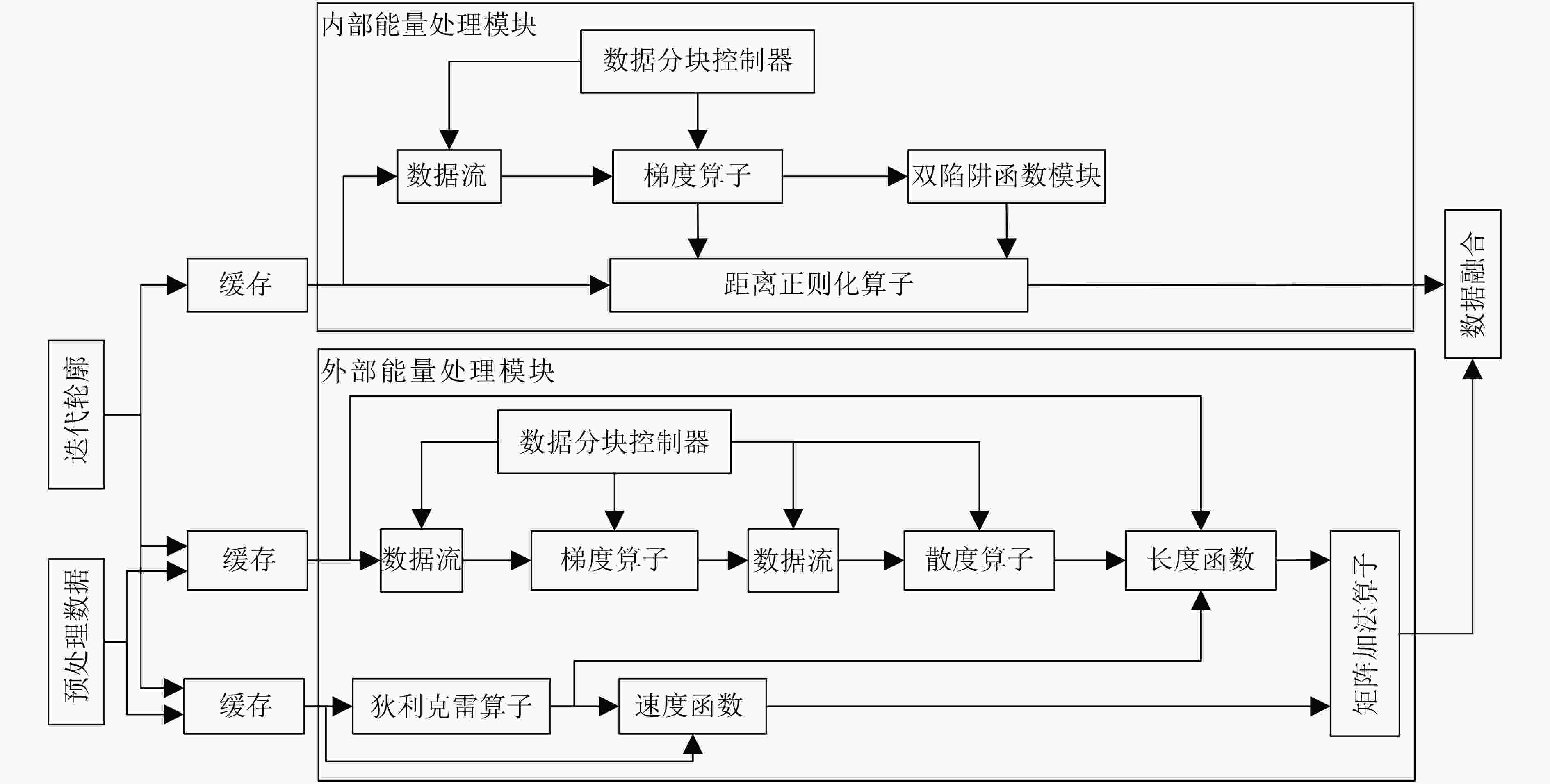
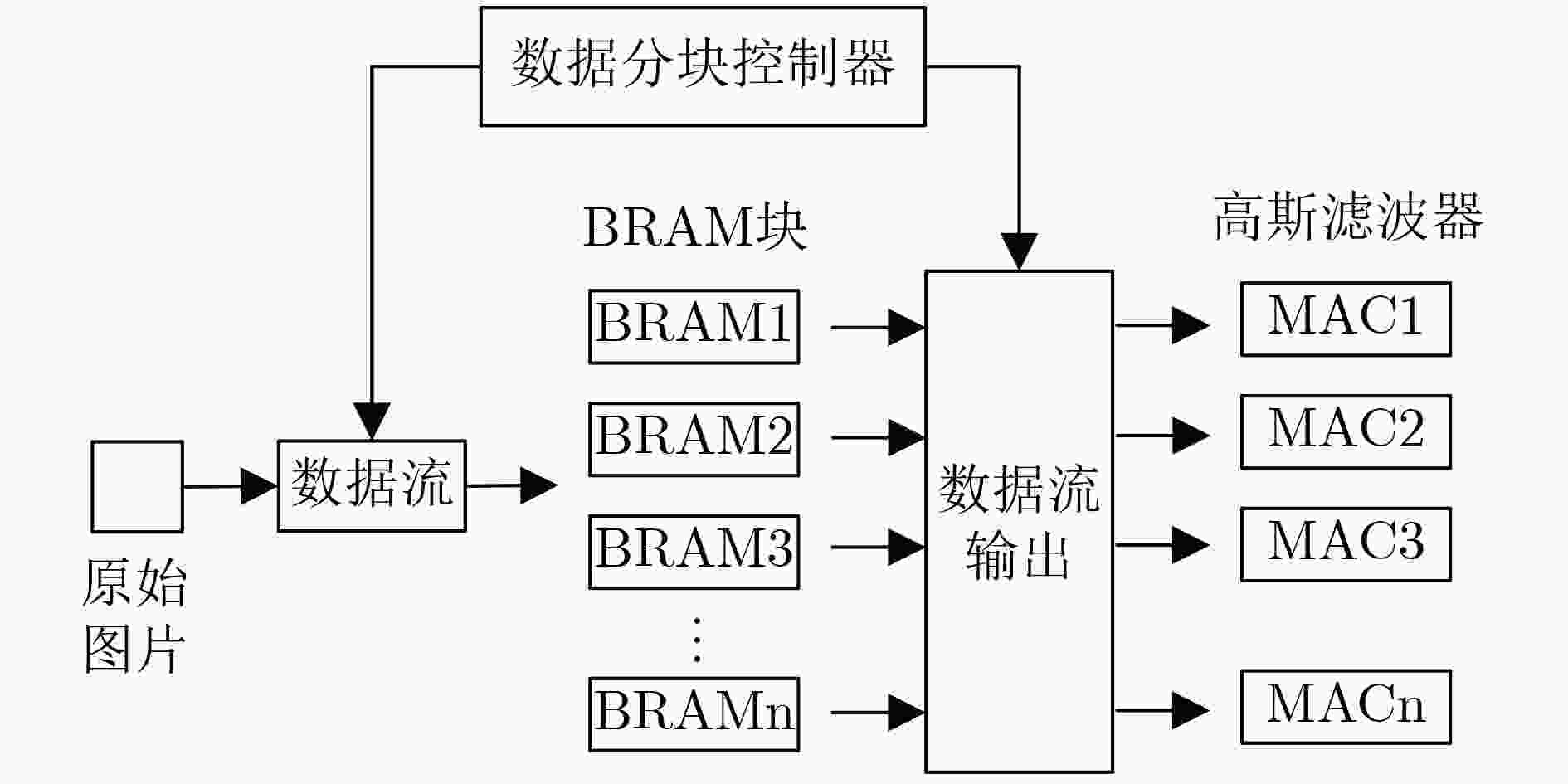
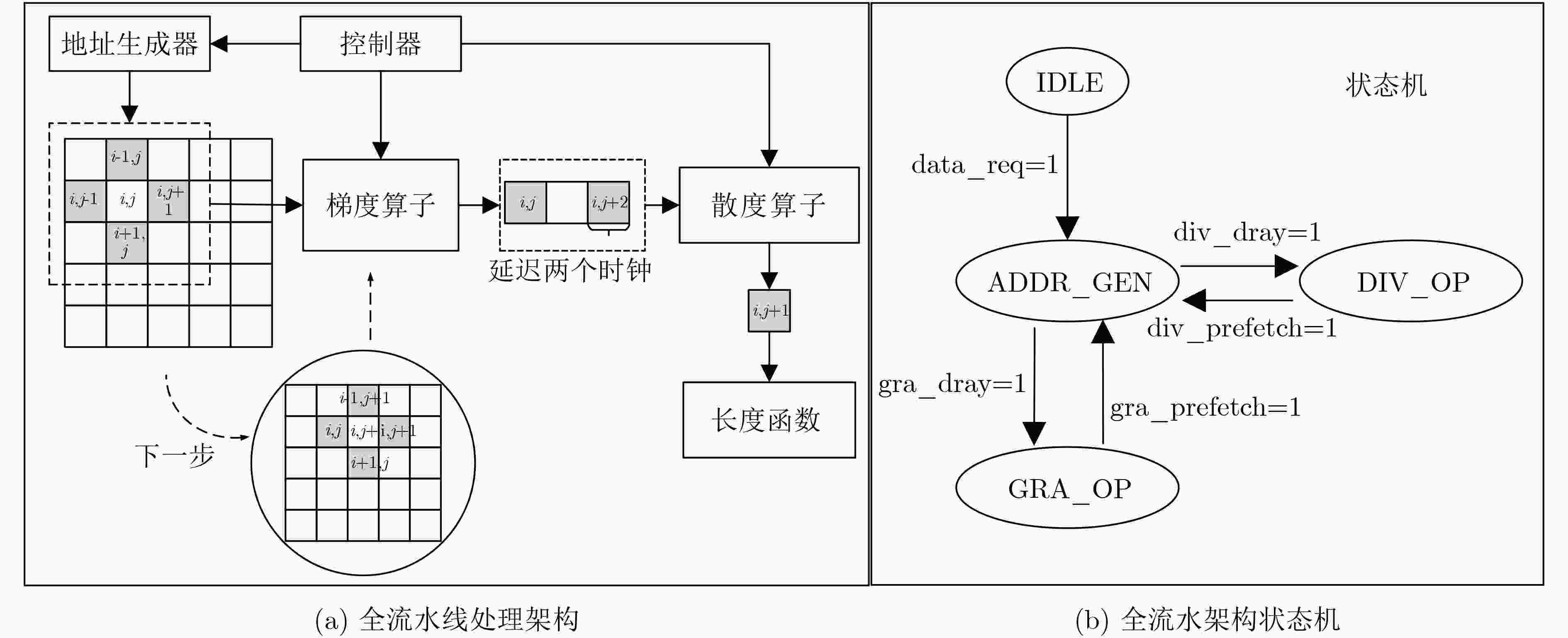
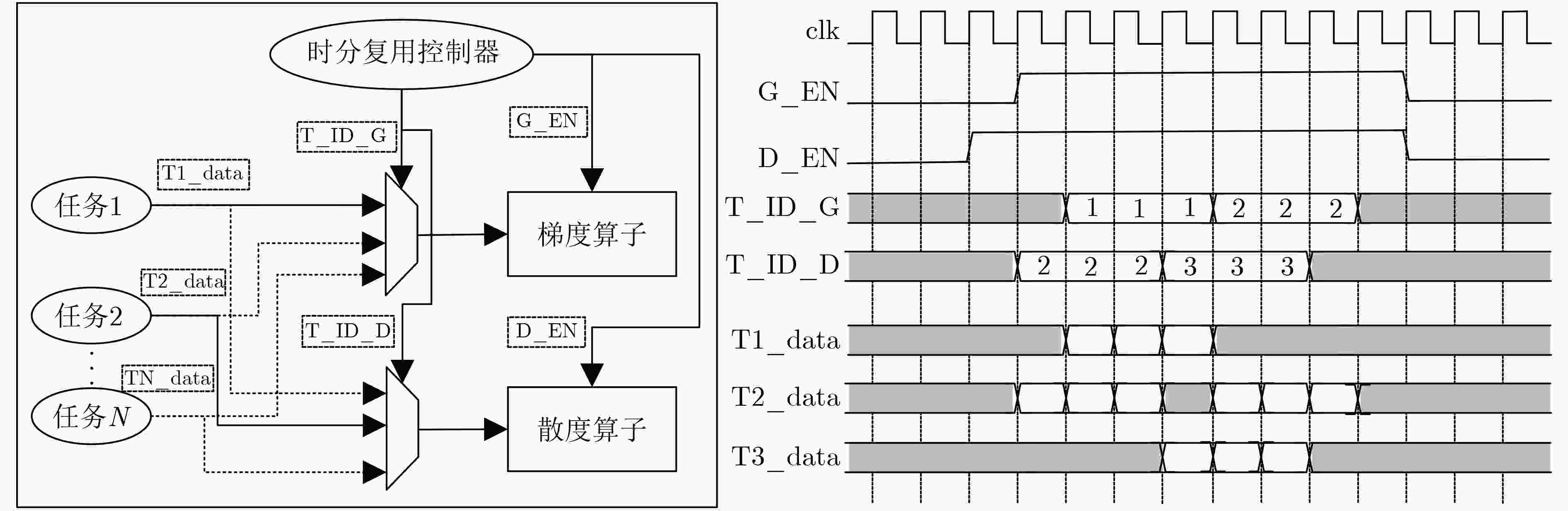
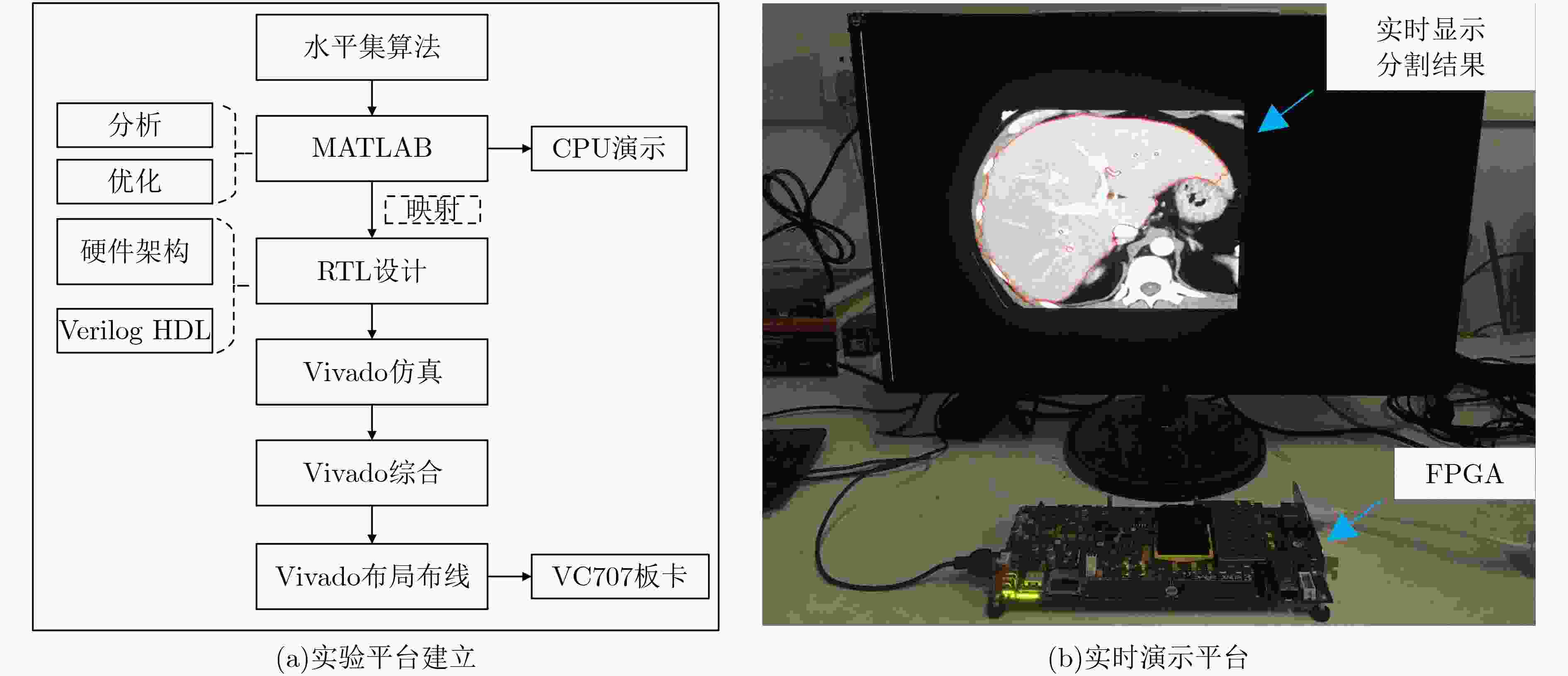
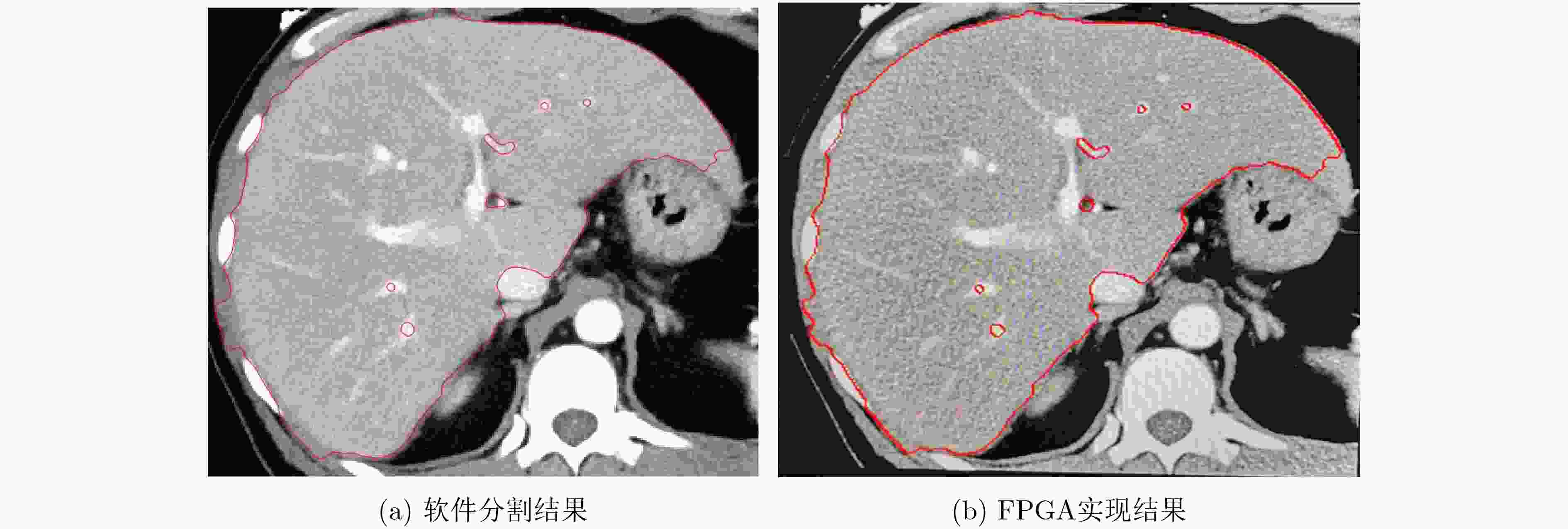
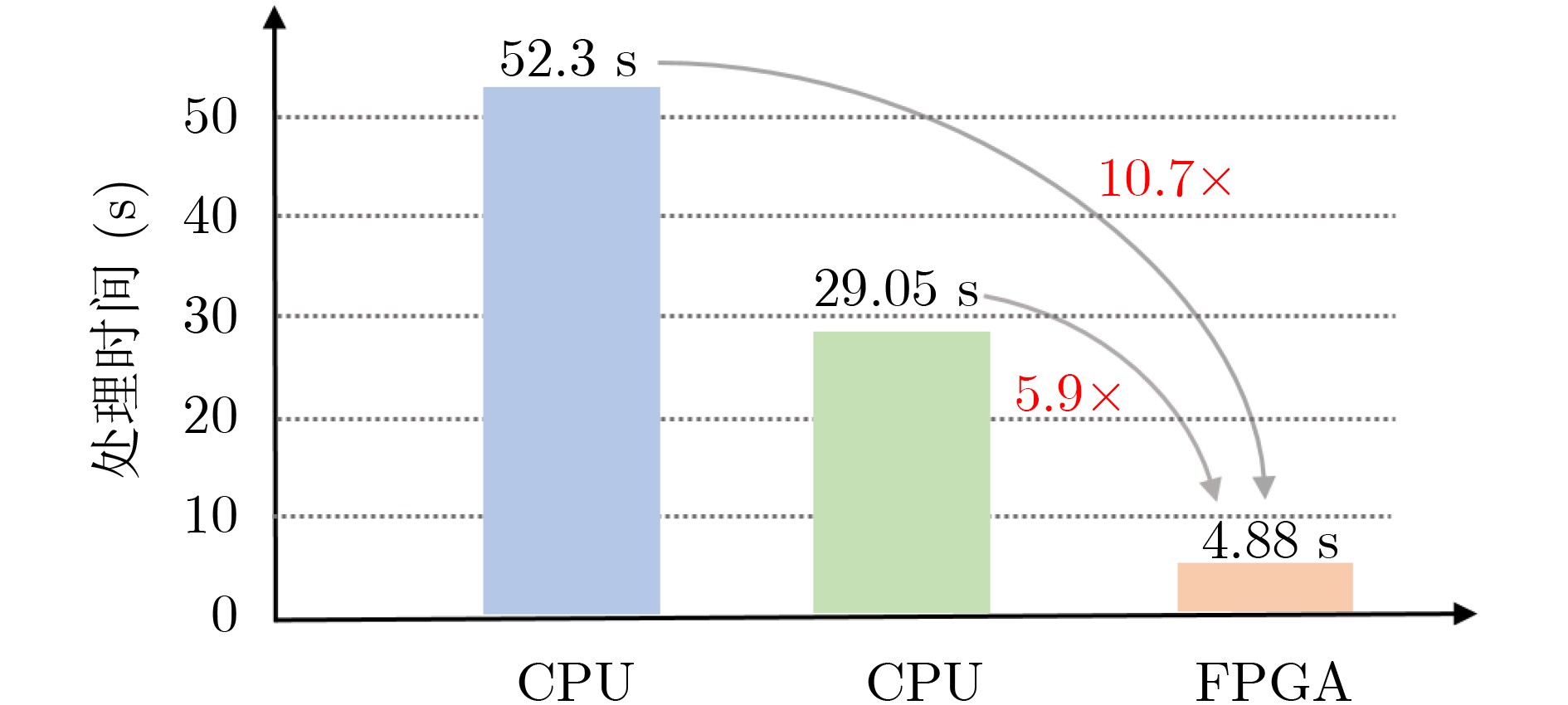
摘要: 水平集算法因其出色的性能，在图像分割领域中得到了广泛的应用。同时，与基于深度学习的图像分割算法相比，水平集算法不需要训练数据，大幅降低了数据标记带来的工作量。然而，目前水平集算法主要是基于软件开发，涉及大量复杂的计算，以及计算的多次迭代，导致较高的处理延时与功耗。为了加快水平集算法的处理速度和降低功耗，该文提出了一种基于FPGA的水平集图像分割算法加速器，其中包含4个设计创新点：任务级并行处理、图像分块像素级并行处理、全流水线处理架构、分时复用的梯度和散度算子处理。实验结果表明，与在CPU上执行的水平集算法相比，该文提出的硬件加速器处理速度提升10.7倍，功耗仅为2.2 W。Abstract: The level set algorithm is widely used for image segmentation due to its high accuracy. In addition, compared to the deep learning-based image segmentation methods, the level set algorithm can be implemented without training data, which reduces significantly the labeling efforts. However, the normal level set algorithm is still developed using software, involving complex computation with a large number of pixels and iterations andcausing long processing time and large power consumption. In this work, an FPGA-based level set hardware accelerator is proposed for image segmentation. The proposed hardware accelerator contains four design components: task-level parallel processing, image splitting processing, fully-pipelined processing architecture, and time-multiplexed gradient and divergence processing engine. Based on the experimental results, the proposed hardware accelerator achieves up to 10.7 times acceleration compared to the level set algorithm executing on the CPU, with only 2.2 W power consumption.
-
Key words:
- FPGA /
- Hardware accelerator /
- Level set /
- Image segmentation
-
1. 引言
图像分割技术已经广泛应用于多个领域，如医学图像分析、自动驾驶、人脸识别等[1-3]。该技术可以独立应用或作为目标检测和目标分类应用的预处理方法。图像分割可以使用传统的分割方法实现(如水平集方法)，也可以使用基于神经网络的方法。其中，基于神经网络的图像分割方法比如全卷积网络(Fully Convolutional Networks, FCN)和U-Net[4]，由于其高准确率的特点，在近几年吸引了大量关注。但是这些方法的缺点是需要大量的训练数据才能达到如此高的准确率。为了制作图像分割的标签，需要为每个训练的数据画出目标轮廓，这往往需要耗费大量精力和时间。与基于神经网络的方法对比，基于水平集的图像分割方法不需要训练数据并且能够达到高准确率。另外，基于水平集的图像分割方法是根据像素纹理进行分割的，与需要训练数据的神经网络方法相比，提供了更强的鲁棒性。
水平集方法由Osher等人[5]首次提出，用于捕获动态的图像轮廓。随后，Kass等人[6]提出了基于活动轮廓模型的改进算法。活动轮廓模型有两种类型：参数活动轮廓模型[6,7]和几何活动轮廓模型[8-10]。水平集算法的关键点是曲线演化理论，即使用高维曲面的零平面表示低维曲面的轮廓。水平集方法与其他的图像分割方法对比的一个优点是它能够很好地处理拓扑结构变化的问题(比如在演化过程中，轮廓的拓扑结构从1个轮廓分化为两个轮廓，或者从两个轮廓合并为1个轮廓的情况)。
对比基于深度学习的图像分割方法[11]，水平集方法具有无需训练数据、准确率高的特点，显著地减少了制作标签消耗的时间。但是，该算法包含了大量的复杂计算和多次迭代的过程，导致计算复杂度很高。在水平集算法中，基于能量泛函的偏微分方程涉及大量的梯度和散度计算，并且在曲线轮廓演进的过程中，需要重复计算该过程。此外，迭代计算的过程需要应用于整张图片的全部像素，从而进一步增加了计算复杂度。目前，水平集算法仍然通过中央处理器(Central Processing Unit, CPU)利用软件实现。复杂的计算过程导致该算法处理时间长和功耗大等问题，严重限制了水平集算法的应用。
为了解决该问题，本文提出了一种基于现场可编程门阵列(Field Programmable Gate Array, FPGA)的水平集图像分割算法加速器[12]。为了加速水平集算法并且提高硬件资源的高利用率，本文提出了4个设计创新点：(1)任务级并行处理；(2)图像分块像素级并行处理；(3)全流水线处理；(4)分时复用的梯度和散度算子处理。实验结果表明：与CPU运行的水平集算法相比，所提出的基于FPGA的水平集图像分割算法加速器有着更高的处理速度。
本文的其余部分内容安排如下：第2节介绍水平集算法；第3节描述本文提出的基于FPGA的水平集图像分割算法加速器以及4个设计创新点；第4节展示实验结果与分析；第5节总结全文。
2. 水平集算法
水平集算法是跟踪轮廓和图像纹理运动的数字方法[13,14]，算法的关键点是通过高维曲面的零水平面来表示低维曲面的轮廓，而非直接求取轮廓信息。高维曲面由水平集函数表示，通过对水平集函数进行微分，并计算零水平集以获得图像轮廓。我们知道，3维曲线的表面可以用一个2维平面的闭合曲线表示，比如2维函数
x2+y2=1 可以表示为{(x,y)|f(x,y)=x2+y2+1=2} ，其中平面是2，集合属于{x2+y2=1} 。因此，水平集算法的优点是可以对任意复杂的结构进行建模和拓扑转换。在原始的水平集算法中，经过多次迭代后，水平集函数需要重新初始化，以确保水平集曲线的平滑度。通过使用新的变分公式[15]以及距离正则化的水平集演化算法 (Distance Regularized Level Set Evolution, DRLSE)[16]，将不再需要重新初始化水平集函数。关于水平集算法的软件处理流程如图1所示。原始的输入图像先经过高斯滤波器处理，然后再进行梯度运算。同时，初始的轮廓使用Neumann边缘函数处理，然后分别进行梯度运算和狄利克雷函数处理。经过3个函数的处理后，可以获得能量函数，根据迭代次数和轮廓的收敛情况判断下一次迭代是否继续进行。DRLSE算法的细节描述如下：
首先，定义一个水平集函数
∅ ，其演化方程如式(1)所示，其中F是速度函数，它取决于图像数据和水平集函数∅ ∂∅∂t+F|∇∅|=0 (1) 然后，定义能量函数
ε ，如式(2)所示，其中RP 是水平集函数的正则项，Lg 是边界指示函数的零水平面轮廓的积分，而Ag 是分割区域的权重。式(3)，式(4)和式(5)分别定义RP ,Lg 和Ag ，其中g是边界指示函数，δ(∅) 是狄利克雷函数，而H(−∅) 是Heaviside函数。ε(∅)=μRP(∅)+λLg(∅)+αAg(∅) (2) ∂RP∂∅=−div(dP(|∇∅|)∇∅) (3) Lg(∅)≜∫Ωgδ(∅)|∇∅|dx (4) Ag(∅)≜∫ΩgH(−∅)dx (5) 结合以上方程式和使能量函数ε降低的梯度[17]演化方程式(6)，可以得出迭代方程式(7)，利用梯度优化方法使能量函数结果降低，可以使目标轮廓收敛。
∂∅∂t=−∂ε∂∅ (6) ∂∅∂t=μdiv(dP(|∇∅|)∇∅)+λδ(∅)⋅div(g∇∅|∇∅|)+αgδ(∅) (7) 从水平集算法的细节可以看出，其计算过程非常复杂，涉及大量的迭代过程。此外，每次迭代都需要遍历整个图像，从而导致处理时间长、功耗高。近年来，一些工作提出了使用CPU+图形处理器(Graphic Processing Unit, GPU)的方法来加速水平集算法的处理[18,19]。
相比于CPU，GPU以其较高的并行计算度在算法加速中具有较大优势，可以通过大量的并行计算引擎加速算法中矩阵或张量的密集运算，但是，在水平集算法中，由于其算法处理的特殊性，不只有高密度矩阵运算，同时还兼有很多逻辑串行计算，这就导致GPU和CPU之间需要进行频繁的数据交互，一方面降低了计算的加速效果，另一方面，增加了数据传输所带来的额外功耗，因此GPU并不是加速水平集算法的最佳选择。在参考文献[18,19]中，为了解决这个问题，对原有水平集算法进行了大量修改，提高了并行度，做了稀疏化处理，并对算法流程进行了修改，才能让该算法可以在GPU上高速运行。然而，该算法降低了原有水平集算法的准确性。
众所周知，CPU按照串行方式执行程序，从水平集算法层面来看，它的每次迭代都需要遍历整个图像的像素。因此，使用CPU执行水平集算法的效率非常低，并且功耗很高。尽管GPU专用于图像处理，但它也是通用图像处理器，与专用硬件架构相比，它不能针对特定算法采用高效策略，这也是造成其低能效和高功耗的原因。
在我们的工作之前，只有文献[20]曾做过关于水平集图像分割算法加速器的工作，但是该算法与我们的算法完全不同，因为它是一种轻量级的水平集算法，提高了性能但牺牲了准确性，并且该作者使用了不同的测试图像和方法，这使得很难比较这两种设计。为了提高能效并加速水平集算法，本文提出了一种基于FPGA的水平集图像分割算法加速器。
3. 水平集图像分割算法硬件架构
本文提出的基于FPGA的水平集图像分割算法加速器的总体硬件架构如图2所示。对应处理流程如下：首先对原始图像中的像素进行预处理，包括高斯滤波去噪、计算图像像素的梯度，通过边缘指示计算模块进行数据转换。然后，进入迭代阶段。对初始化或迭代轮廓进行Neumann边界处理，得到内外能量处理模块的输入。在进行外部能量处理时，将预处理后的数据与Neumann边界处理后的轮廓进行融合作为外部能量模块的输入，然后将内部能量处理模块与外部能量处理模块的输出传输到矩阵加法算子模块进行进一步处理。
为了提高处理速度，本文提出了4种设计技术，包括(1)任务级并行处理；(2)图像分块像素级并行处理；(3)全流水线处理；(4)分时复用的梯度和散度算子处理。它们的细节将在后面的小节中描述。
3.1 任务级并行处理架构
本文提出的任务级并行处理架构如图3所示。通过对水平集算法中子任务的相关性研究，本文发现了多个彼此不相关的子任务。因此，可以通过并行处理这些任务来提高整体处理速度。
可以利用的任务级并行之一是内部和外部能量处理子任务。本文将迭代轮廓缓存在多个并行的缓存区中，而不是缓存在单个缓存区中。这样的好处在于：内部和外部能量处理模块可以同时读取/写入缓存区以并行处理，而且不会发生任何资源的调用冲突。
另一个可以利用的任务级并行是在内部和外部能量处理模块的内部。对于内部能量处理模块而言，可以对梯度和距离正则化的计算进行并行化处理。而对于外部能量处理模块，可以并行计算梯度和狄利克雷函数。综上，本文可以充分利用任务级并行性来提高处理速度。
3.2 图像分块像素级并行处理架构
除任务级的并行性外，像素级的并行性也可以被利用。图4展示了本文提出的图像分块像素级并行处理架构。我们发现在水平集算法中，每个像素的处理只与该像素周围的小部分像素相关，而与其他像素无关。因此在设计硬件架构的时候，本文将输入图像分割成多个图像块并存储在多个随机存取存储器(Random Access Memory, RAM)中，这些RAM中的数据会被并行处理以提高处理速度。例如，在进行高斯滤波平滑处理的过程中，左上角和右下角的图像是互不相关的，因此可以通过将图像分割成4块来同时处理这两个部分的图像。同时为了保证数据处理的完整性和正确性，本文设计了数据分块控制器来处理相邻两个数据块之间的边缘部分。最后，引入的数据分块控制器模块只增加了少量的硬件开销，但大大提高了图像分割迭代过程的收敛速度。
3.3 全流水线处理架构
本文提出的全流水线处理架构如图5所示，其中水平集算法会在流水线控制器的控制下完全流水化处理。一旦模块的输入数据准备好，就会立即开始该模块的数据处理。通过在不同级别(系统级和模块级)设计全流水线的处理结构，可以充分利用所有的处理模块来提高吞吐量。流水线机制需要有一个状态机来控制协调，如图5(a)所示，它主要分为地址生成状态、梯度计算状态和散度计算状态，对应的控制信号如图5(b)所示，当发送数据请求发生时，它将跳转到地址生成状态，并通过内部计数器确定梯度计算是否开启以及散度计算是否开启。例如，对于外部能量处理模块，可以实现梯度函数、散度函数、轮廓长度函数的流水线化。当梯度计算完成后，其结果将直接传递到下一阶段；一旦数据准备好，散度的计算将立即开始；当散度计算完成后，轮廓长度的计算也可以立刻开始。全流水线的处理架构大大提高了吞吐量。
3.4 分时复用架构
为了减少资源使用量，本文设计了分时复用的梯度和散度算子处理模块，如图6所示。在水平集算法中，有一些处理阶段需要计算像素的梯度和散度。由于这些阶段不需要同时工作，并且这些阶段之间的时间间隔很长，所以可以对梯度和散度计算模块进行分时复用。本文通过设计一个分时复用控制器来实现，它可以动态地切换梯度和散度计算模块的数据输入/输出，并控制模块的启动/停止。这种设计有助于减少硬件开销，同时不影响处理速度。
4. 实验结果
本节介绍用于验证所提出的水平集图像分割算法加速器的实验设备搭建和实时演示平台。然后，根据Xilinx Vivado平台的评估结果来分析实验结果。
图7(a)展示了实验设备的搭建流程，其中包括算法分析和优化、硬件架构设计以及FPGA实现。在算法分析中，本文抽象了水平集算法的关键部分，以加快执行速度。在硬件架构设计中，设计了任务级并行处理架构、图像分块像素级并行处理架构、全流水线处理架构、分时复用的梯度和散度算子处理架构，组成了硬件的加速平台。在FPGA实现中，采用Xilinx VC707 FPGA评估板来实现提出的定点数据的水平集图像分割算法加速器。使用Xilinx Vivado平台来验证Verilog HDL语言描述的RTL行为，并生成比特流以供验证评估。
图7(b)展示了实验的实时演示平台，包括一个显示器、Xilinx VC707 FPGA评估板和必要的连接器。将水平集图像分割算法加速器应用于图像分割，图像存储在FPGA中，通过按FPGA板上的按键开始进行分割。同时，中间迭代的分割轮廓被传输到显示器上进行实时显示。
图8显示了软件和FPGA实现的分割结果对比，其错误率小于1.8%。测试的医学电子计算机断层扫描(Computed Tomography, CT)图像的像素尺寸为270×300，FPGA的工作时钟频率为100 MHz。在FPGA上实现的分割结果与软件的结果匹配，但是通过FPGA实现的分割速度提升很多。其中CPU的型号为1.80 GHz的Intel Core i5-8250U，内存为8 GB，硬件平台为Xilinx VC707 FPGA评估板。在运行功率为50 W的情况下，软件实现对图像进行分割的处理时间为52.3 s，而在运行功率为2.2 W的情况下，FPGA实现的处理时间仅为4.88 s，比软件实现的处理时间减少了10.7倍。为了更好地展示本文架构的性能，将算法进一步通过GPU进行了实现，GPU型号为GeForce RTX 2080，分割时间为29.05 s，FPGA硬件架构与其相比，加快5.9倍，如图9所示。图10展示了3张对其他图像的分割轮廓结果，并给出了参考轮廓以及IoU值，IoU均能达到95%以上。
表1显示了FPGA的资源利用率。Virtex 7以100 MHz的时钟频率来运行本文提出的硬件加速器。可以看到，Xilinx Virtex 7 FPGA芯片的所有资源使用率只有10%左右，因此所提出的水平集图像分割算法加速器是轻量级的。图11展示了所提出的水平集图像分割算法加速器的功耗以及功耗的详细占比。在使用Xilinx Virtex 7 FPGA分割270×300医学图像时，硬件加速器的功率为2.2 W。在功耗的占比中，动态功耗占85%，包括了BRAM、信号、逻辑、DSP和时钟上的功耗。
表 1 资源利用率FPGA型号 时钟频率 (MHz) Regs LUT DSP Virtex7 100 40655(6.69%) 30680(10.10%) 307(10.96%) 5. 结论
本文提出了一种基于FPGA的水平集图像分割算法加速器，以提高水平集图像分割算法的处理速度和能效。其中，提出了4种设计技术，包括任务级并行处理、图像分块像素级并行处理、全流水线处理架构和分时复用的梯度和散度算子处理。在Xilinx VC707 FPGA评估板上实现了水平集图像分割算法加速器，并且得到了与软件处理结果相同的分割轮廓。基于FPGA实现的水平集图像分割算法结果与软件实现的分割结果基本一致，分割速度提升10.7倍，功耗仅为2.2 W。
-
表 1 资源利用率
FPGA型号 时钟频率 (MHz) Regs LUT DSP Virtex7 100 40655(6.69%) 30680(10.10%) 307(10.96%) 
下载: 导出CSV
-
[1] NIRKIN Y, MASI I, TRAN TUAN A, et al. On face segmentation, face swapping, and face perception[C]. Proceedings of the 13th IEEE International Conference on Automatic Face & Gesture Recognition (FG 2018), Xi'an, China, 2018: 98–105. doi: 10.1109/FG.2018.00024. [2] WANG Guotai, LI Wenqi, ZULUAGA M A, et al. Interactive medical image segmentation using deep learning with image-specific fine tuning[J]. IEEE Transactions on Medical Imaging, 2018, 37(7): 1562–1573. doi: 10.1109/TMI.2018.2791721 [3] MISHRA S, LIANG Peixian, CZAJKA A, et al. CC-NET: Image complexity guided network compression for biomedical image segmentation[C]. Proceedings of the IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 2019: 57–60. doi: 10.1109/ISBI.2019.8759448. [4] HU Haigen, ZHENG Yixing, ZHOU Qianwei, et al. MC-Unet: Multi-scale convolution unet for bladder cancer cell segmentation in phase-contrast microscopy images[C]. Proceedings of 2019 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), San Diego, USA, 2019: 1197–1199. doi: 10.1109/BIBM47256.2019.8983121. [5] OSHER S and SETHIAN J A. Fronts propagating with curvature-dependent speed: Algorithms based on hamilton-jacobi formulations[J]. Journal of Computational Physics, 1998, 79(1): 12–49. doi: 10.1016/0021-9991(88)90002-2 [6] KASS M, WITKIN A, and TERZOPOULOS D. Snakes: Active contour models[J]. International Journal of Computer Vision, 1988, 1(4): 321–331. doi: 10.1007/BF00133570 [7] XU Chenyang and PRINCE J L. Snakes, shapes, and gradient vector flow[J]. IEEE Transactions on Image Processing, 1998, 7(3): 359–369. doi: 10.1109/83.661186 [8] CASELLES V, CATTÉ F, COLL T, et al. A geometric model for active contours in image processing[J]. Numerische Mathematik, 1993, 66(1): 1–31. doi: 10.1007/BF01385685 [9] CASELLES V, KIMMEL R, and SAPIRO G. Geodesic active contours[J]. International Journal of Computer Vision, 1997, 22(1): 61–79. doi: 10.1023/A:1007979827043 [10] MALLADI R, SETHIAN J A, and VEMURI B C. Shape modeling with front propagation: A level set approach[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(2): 158–175. doi: 10.1109/34.368173 [11] RONNEBERGER O, FISCHER P, and BROX T. U-Net: Convolutional networks for biomedical image segmentation[C]. Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Munich, Germany, 2015: 234–241. doi: 10.1007/978-3-319-24574-4_28. [12] LIU Ye, WANG Yin, CHANG Liang, et al. A fast and efficient FPGA-based level set hardware accelerator for image segmentation[C]. Proceedings of 2020 IEEE International Conference on Integrated Circuits, Technologies and Applications (ICTA), Nanjing, China, 2020: 83–84. doi: 10.1109/ICTA50426.2020.9331957. [13] CHAN T F and VESE L A. Active contours without edges[J]. IEEE Transactions on Image Processing, 2001, 10(2): 266–277. doi: 10.1109/83.902291 [14] LI Chunming, HUANG Rui, DING Zhaohua, et al. A level set method for image segmentation in the presence of intensity inhomogeneities with application to MRI[J]. IEEE Transactions on Image Processing, 2011, 20(7): 2007–2016. doi: 10.1109/TIP.2011.2146190 [15] LI Chunming, XU Chenyang, GUI Changfeng, et al. Level set evolution without re-initialization: A new variational formulation[C]. Proceedings of 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, USA, 2005: 430–436. doi: 10.1109/CVPR.2005.213. [16] LI Chunming, XU Chenyang, GUI Changfeng, et al. Distance regularized level set evolution and its application to image segmentation[J]. IEEE Transactions on Image Processing, 2010, 19(12): 3243–3254. doi: 10.1109/TIP.2010.2069690 [17] EVANS L C. Partial Differential Equations[M]. 2nd ed. USA: American Mathematical Society, 2010. [18] JALBA A C, VAN DER LAAN W J, and ROERDINK J B T M. Fast sparse level sets on graphics hardware[J]. IEEE Transactions on Visualization and Computer Graphics, 2013, 19(1): 30–44. doi: 10.1109/TVCG.2012.69 [19] BALLA-ARABÉ S, GAO Xinbo, and WANG Bin. GPU accelerated edge-region based level set evolution constrained by 2d gray-scale histogram[J]. IEEE Transactions on Image Processing, 2013, 22(7): 2688–2698. doi: 10.1109/TIP.2013.2255304 [20] TSUYAMA H and MARUYAMA T. An FPGA acceleration of a level set segmentation method[C]. Proceedings of the 22nd International Conference on Field Programmable Logic and Applications (FPL), Oslo, Norway, 2012: 414–420. doi: 10.1109/FPL.2012.6339138. 期刊类型引用(4)
1. 张静. 红外图像分割与目标提取方法研究. 智能计算机与应用. 2024(07): 241-245 . 
百度学术2. 黄西莹，张旭辉，黄玉，李涛，宋磊，刘培桢. 基于国产异构FPGA的空中红外目标检测跟踪系统. 红外与激光工程. 2024(08): 114-124 . 百度学术3. 穆向阳，雷妍，王闻博. 一种中值滤波快速系统的FPGA实现. 西安石油大学学报(自然科学版). 2023(02): 128-134 . 百度学术4. 胡新钟，蔡昌新. 基于FPGA的镀层腐蚀形貌特征提取. 电镀与精饰. 2023(06): 90-96 . 百度学术其他类型引用(1)
-
下载:
百度学术
计量
- 文章访问数: 1118
- HTML全文浏览量: 464
- PDF下载量: 142
- 被引次数: 5
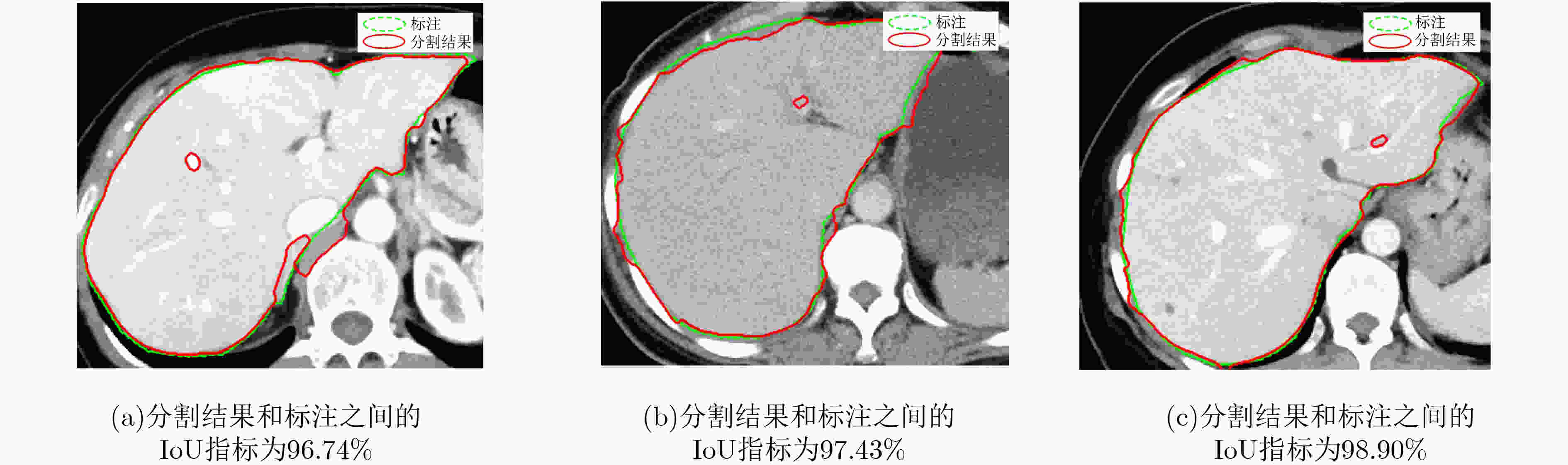
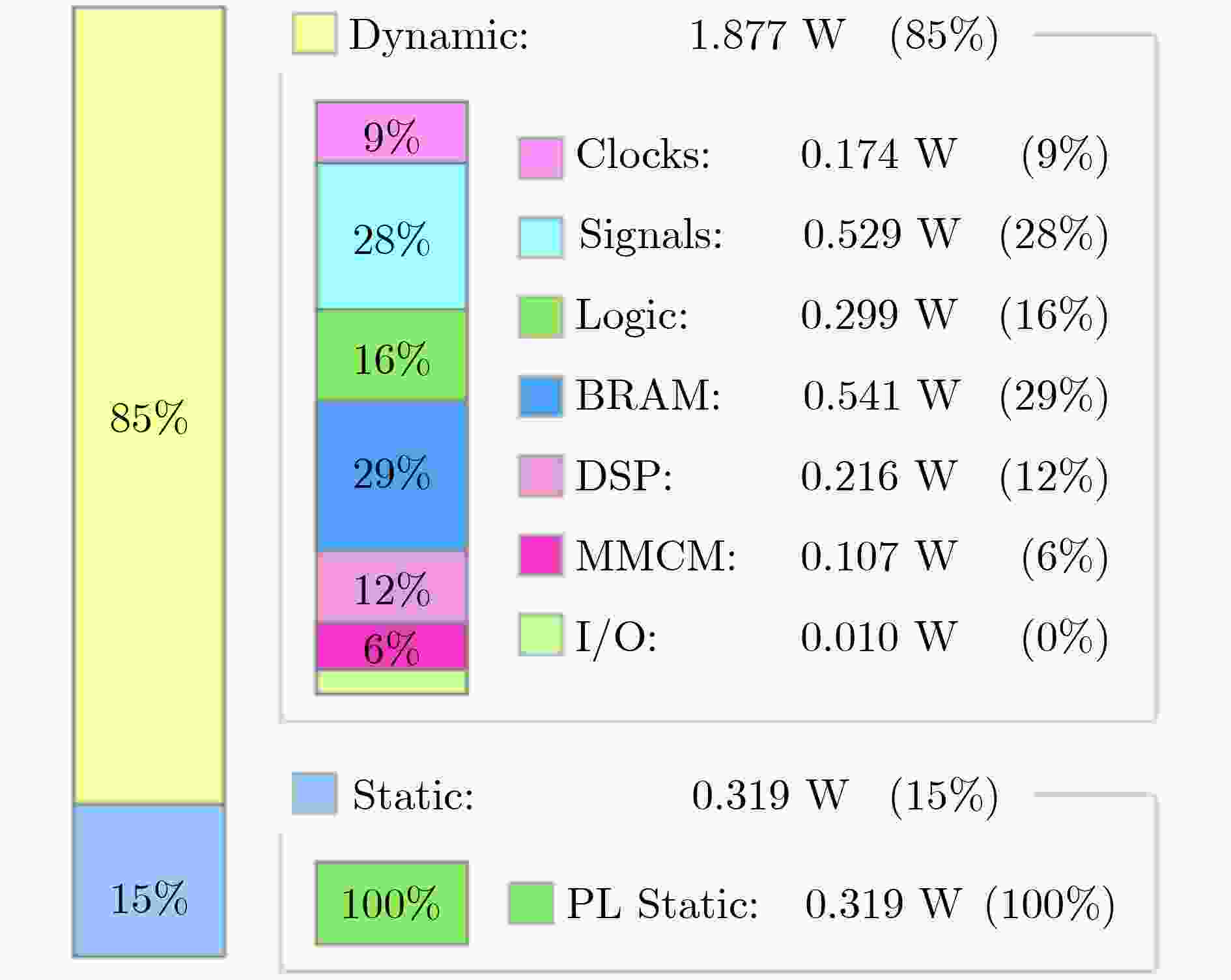
下载:
