Intelligent Multi-carrier Waveform Modulation System: Signal Generation and Recognition
-
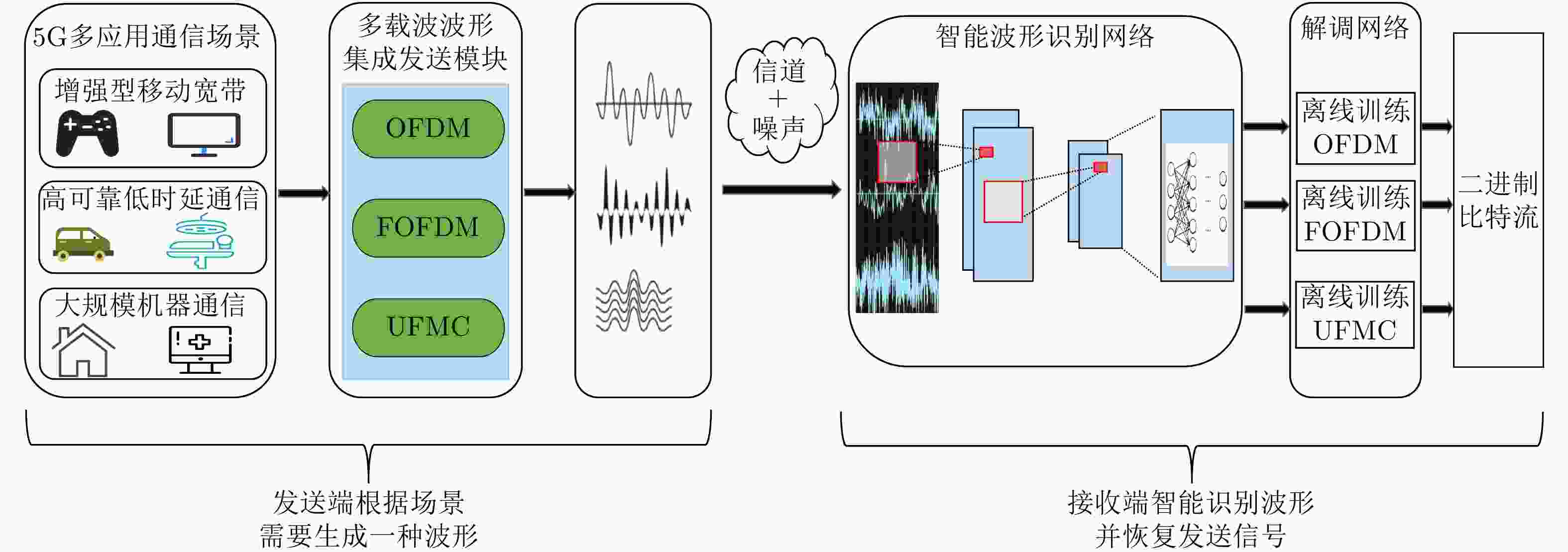
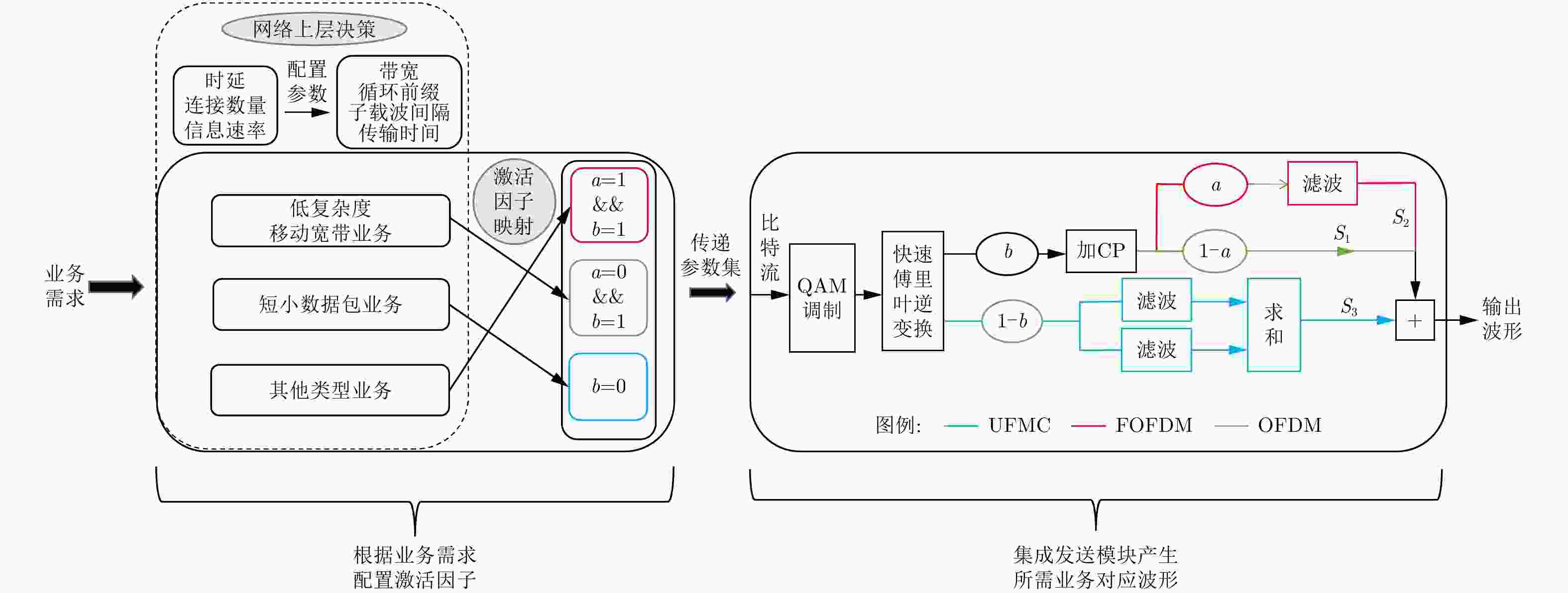
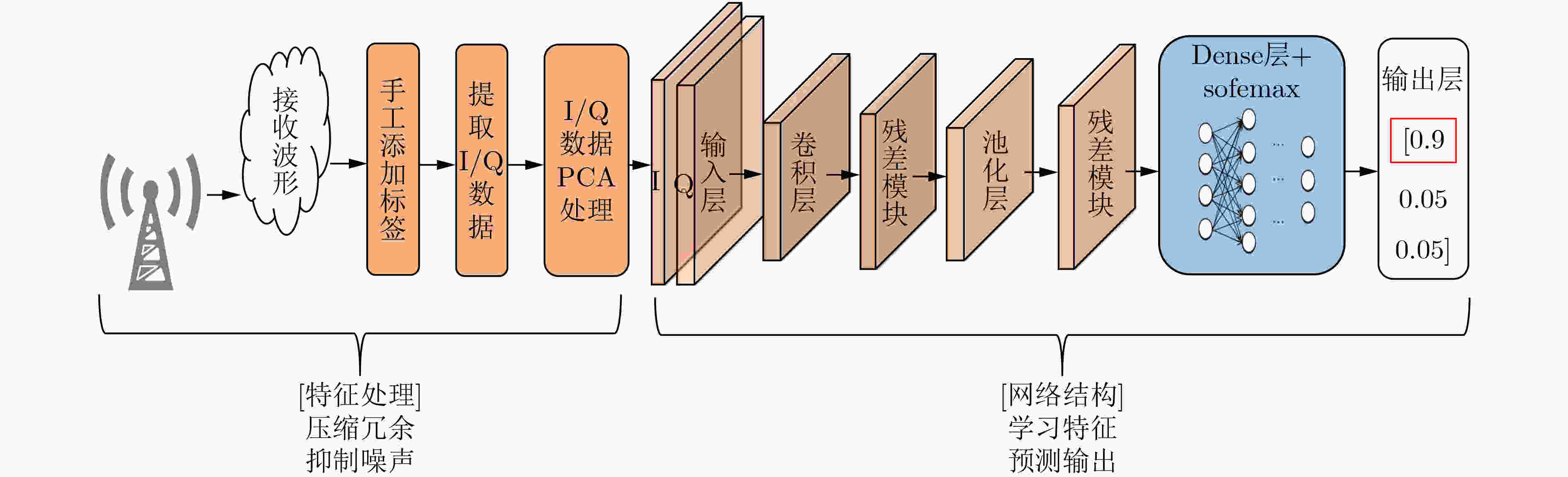
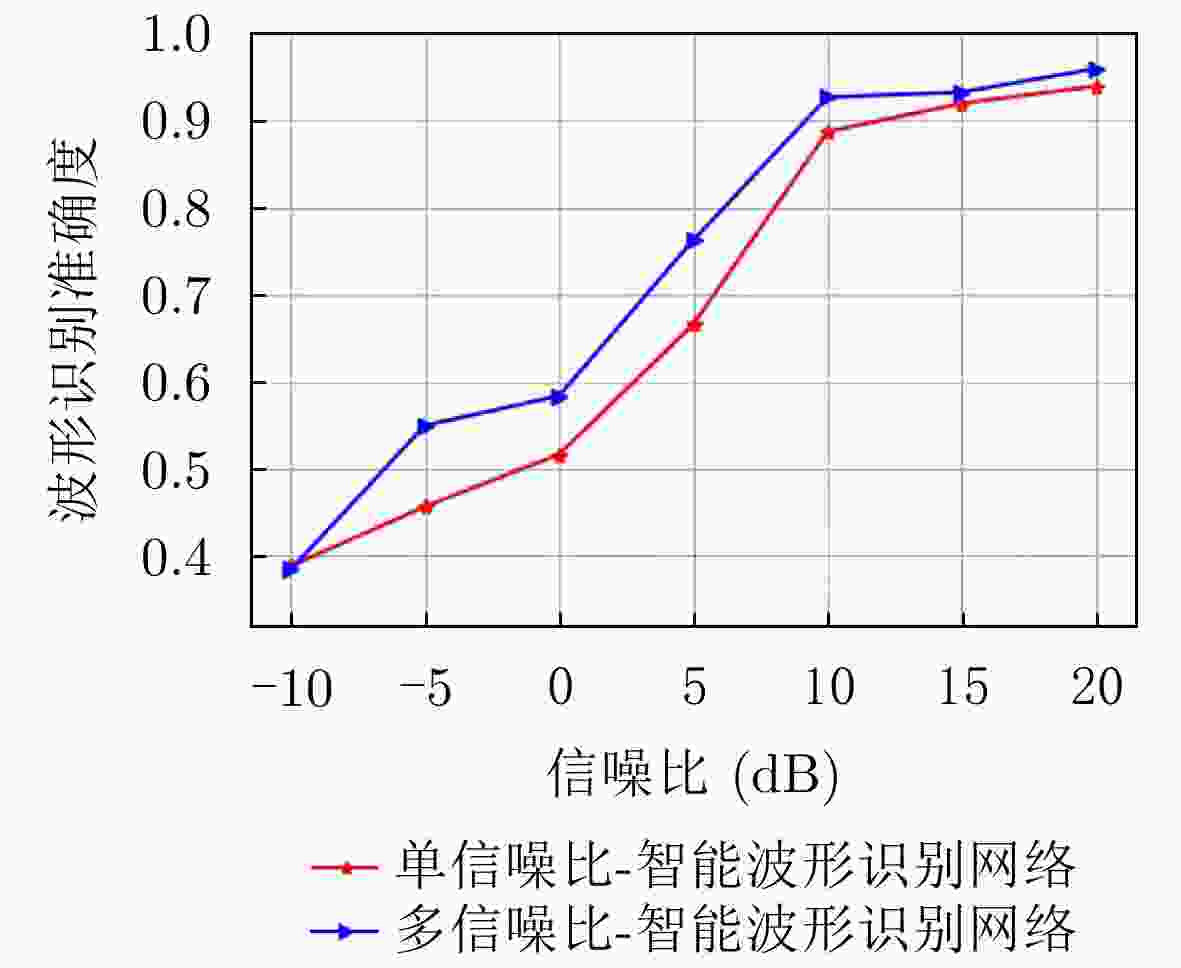
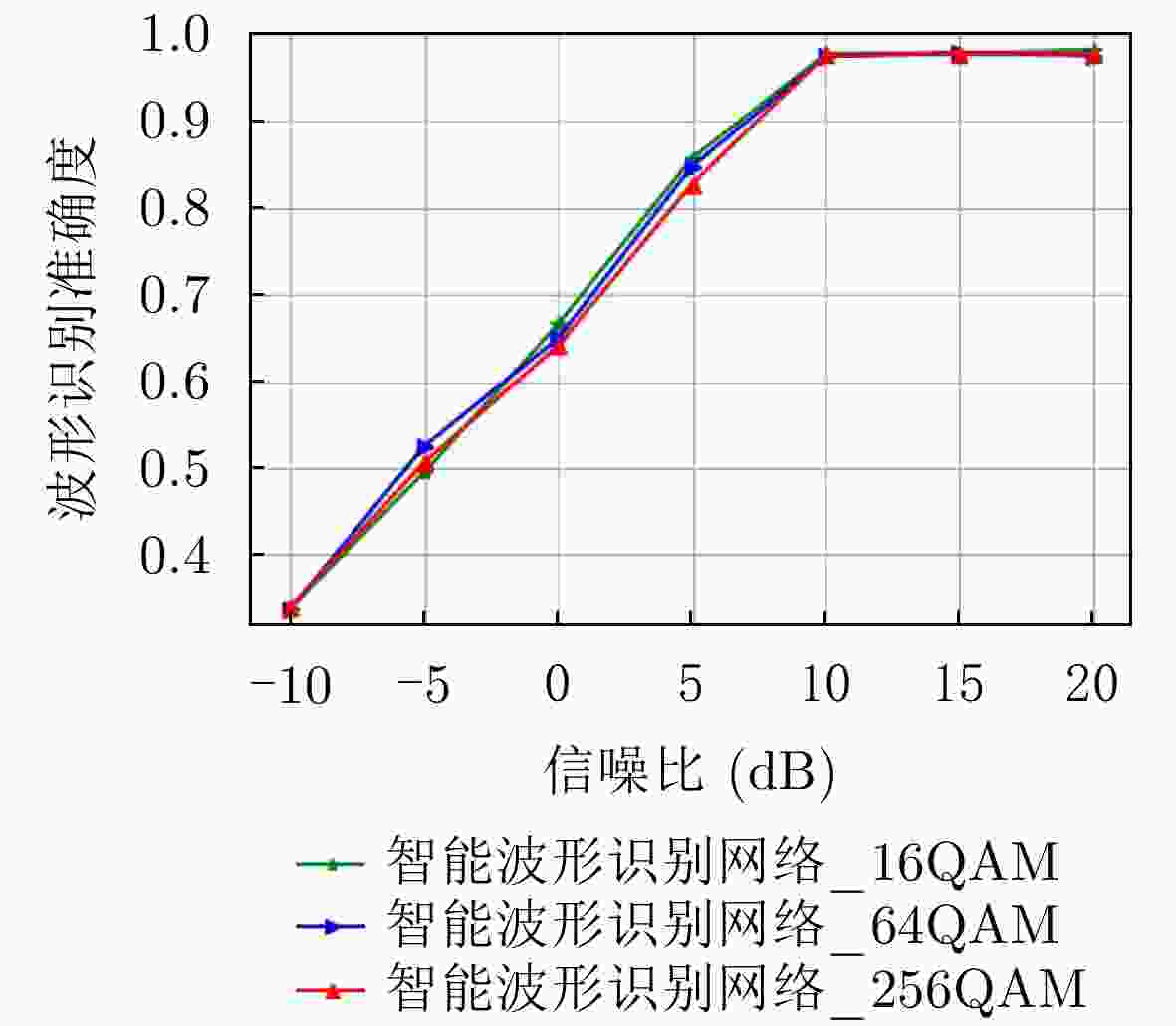
摘要: 移动通信应用场景逐渐呈现复杂化和多变化趋势,很难有一种普适性传输波形满足所有通信需求,这对多种波形的配合与协作提出了较高的要求。该文提出一种适用于复杂场景下的智能化多载波波形调制系统,发送端可通过波形激活因子选择产生合适的传输波形,接收端将不同波形信号的I/Q分量作为自适应因子,使用主成分分析法处理数据后送入智能波形识别网络(IWR-Net)完成信号的识别。所提系统融合深度学习网络,具有较为统一的硬件架构。仿真结果表明,所提方案在5G多场景下对不同发送波形识别准确率最高可达98.2%,并且在不同测试环境中具有良好的泛化性能。
-
关键词:
- 智能化多载波波形调制系统 /
- 多载波波形识别 /
- 深度学习 /
- 智能波形识别网络
Abstract: Mobile communication applications scenarios are becoming complexity and diversity. It is difficult to have a universal transmission waveform to meet all communication needs, which puts forward high requirements for the coordination and collaboration of multiple waveforms. In this paper, an intelligent multi-carrier waveform modulation system is proposed for complex scenarios, the sending end can select a suitable transmission waveform by the waveform activation factor, the receiving end will take the I/Q component of different waveform signals as an adaptive factor, and use the main component analysis method to process the data and feed it into the Intelligent Waveform Recognition Network (IWR-Net) to complete the identification of the signal. The proposed system is integrated with deep learning network and has a more unified hardware architecture. The simulation results show that the accuracy of different send waveform recognition can be as high as 98.2% in 5G multi-scenes, and it has good generalization performance in different test environments. -
表 1 PCA算法处理接收信号流程
输入:原始波形样本数据${\boldsymbol{X}}= ({{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2},\cdots,{{\boldsymbol{x}}_m})_{d \times 2 \times m}^{\rm{T}}$,降维后维度大小${d^*}$; 输出:降维后的波形数据${\boldsymbol{Y}} = ({{\boldsymbol{x}}_1},{{\boldsymbol{x}}_2},\cdots,{{\boldsymbol{x}}_m})_{{d^*} \times 2 \times m}^{\rm{T}}$; (1) for(int j=0; i<3; i++), do
(2) [OFDM, FOFDM, UFMC]: ${ {\boldsymbol{x} }_i} \Leftarrow { {\boldsymbol{x} }_i} - \dfrac{1}{m}\displaystyle\sum\limits_{i = 1}^m { { {\boldsymbol{x} }_i} }$; //对第j种波形数据样本中心化处理(3) ${\boldsymbol{C} } = \dfrac{1}{m}{\boldsymbol{X} }{ {\boldsymbol{X} }^{\rm{T} } }$; //计算波形样本的协方差矩阵 (4) 从最大可分性出发, 构造优化目标: $\mathop { \Rightarrow \max }\limits_{\boldsymbol{w} } \begin{array}{*{20}{c} } {} \end{array}{ {\rm{tr} } }({ {\boldsymbol{W} }^{\rm{T} } }{\boldsymbol{X} }{ {\boldsymbol{X} }^{\rm{T} } }{\boldsymbol{W} }),\;\;{ {\rm{s.t} } } \;\;{ {\boldsymbol{W} }^{\rm{T} } }{\boldsymbol{W} } = {\boldsymbol{I} }$; (5) 使用拉格朗日乘子法得: ${\boldsymbol{X}}{{\boldsymbol{X}}^{\rm{T}}}{\boldsymbol{W}} = \lambda {\boldsymbol{W}}$; (6) 协方差矩阵${\boldsymbol{X}}{{\boldsymbol{X}}^{\rm{T}}}$特征值分解,特征值大小排序后:${\lambda _{\rm{1} } } \ge {\lambda _2} \ge \cdots \ge {\lambda _d}$; (7) 取最大的${d^*}$个特征值所对应的特征向量${{\boldsymbol{\omega}} _{\rm{1}}},{{\boldsymbol{\omega}} _2},\cdots,{{\boldsymbol{\omega}} _{{d^*}}}$组成矩阵${\boldsymbol{P}}$; (8) 计算降维后的矩阵${\boldsymbol{Y}}= {\boldsymbol{P}}{\boldsymbol{X}}$; (9) end 表 2 系统参数配置
参数 数值 参数 数值 FFT长度 256 卷积层激活函数 ReLU 映射方式 16QAM Dropout率 0.3 子带大小 10 过滤器数量 32 子带偏移 78 过滤器大小 (3,2) 切比雪夫滤波器长度 73 优化器 Adam 旁瓣衰减 40 dB 最大池化层大小 (2,2) CP长度 73 全连接层神经元数量 128 表 3 模型训练及测试运行时间(s)
模型 训练时间 测试时间 – – OFDM FOFDM UFMC 多信噪比模型 684.60 3.30 3.26 3.27 单信噪比模型 874.52 3.24 3.76 3.34 -
[1] AAZHANG B, AHOKANGAS P, ALVES H, et al. Key drivers and research challenges for 6G ubiquitous wireless intelligence[EB/OL]. http://jultika.oulu.fi/files/isbn9789526223544.pdf, 2019. [2] TOMKOS I, KLONIDIS D, PIKASIS E, et al. Toward the 6G network era: Opportunities and challenges[J]. IT Professional, 2020, 22(1): 34–38. doi: 10.1109/MITP.2019.2963491 [3] SAAD W, BENNIS M, and CHEN Mingzhe. A vision of 6G wireless systems: Applications, trends, technologies, and open research problems[J]. IEEE Network, 2020, 34(3): 134–142. doi: 10.1109/MNET.001.1900287 [4] SADI Y, ERKUCUK S, and PANAYIRCI E. Flexible physical layer based resource allocation for machine type communications towards 6G[C]. 2020 2nd 6G Wireless Summit (6G SUMMIT), Levi, 2020: 1–5. doi: 10.1109/6GSUMMIT49458.2020.9083921. [5] SAHIN A, GUVENC I, and ARSLAN H. A survey on multicarrier communications: Prototype filters, lattice structures, and implementation aspects[J]. IEEE Communications Surveys & Tutorials, 2014, 16(3): 1312–1338. doi: 10.1109/SURV.2013.121213.00263 [6] MT-2020(5G)推进组. IMT-2020(5G)推进组发布5G技术白皮书[J]. 中国无线电, 2015(5): 6.IMT-2020 Promotion Group. 5G wireless technology architecture white paper[J]. China Radio, 2015(5): 6. [7] VIHRIALA J, ERMOLOVA N, LAHETKANGAS E, et al. On the waveforms for 5G mobile broadband communications[C]. 2015 IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, Scotland, 2015: 1–5. doi: 10.1109/VTCSPRING.2015.7145977. [8] HAN Shuangfeng, XIE Tian, CHIH-LIN I, et al. Artificial-intelligence-enabled air interface for 6G: Solutions, challenges, and standardization impacts[J]. IEEE Communications Magazine, 2020, 58(10): 73–79. doi: 10.1109/MCOM.001.2000218 [9] YUAN Yabo, ZHAO Peng, WANG Bo, et al. Hybrid maximum likelihood modulation classification for continuous phase modulations[J]. IEEE Communications Letters, 2016, 20(3): 450–453. doi: 10.1109/LCOMM.2016.2517007 [10] WANG Hui and GUO Lili. A new method of automatic modulation recognition based on dimension reduction[C]. 2017 Forum on Cooperative Positioning and Service (CPGPS), Harbin, China, 2017: 316–320. doi: 10.1109/CPGPS.2017.8075146. [11] SU Wei. Feature space analysis of modulation classification using very high-order statistics[J]. IEEE Communications Letters, 2013, 17(9): 1688–1691. doi: 10.1109/LCOMM.2013.080613.130070 [12] O’SHEA T J, ROY T, and CLANCY T C. Over-the-air deep learning based radio signal classification[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 168–179. doi: 10.1109/JSTSP.2018.2797022 [13] WANG Yu, LIU Miao, YANG Jie, et al. Data-driven deep learning for automatic modulation recognition in cognitive radios[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 4074–4077. doi: 10.1109/TVT.2019.2900460 [14] DUAN Sirui, CHEN Kan, YU Xiang, et al. Automatic multicarrier waveform classification via PCA and convolutional neural networks[J]. IEEE Access, 2018, 6: 51365–51373. doi: 10.1109/ACCESS.2018.2869901 [15] 邵凯, 李述栋, 王光宇, 等. 基于迟滞噪声混沌神经网络的导频分配[J]. 电子与信息学报, 2020, 42(10): 2454–2461. doi: 10.11999/JEIT190748SHAO Kai, LI Shudong, WANG Guangyu, et al. Hysteretic noisy chaotic neural networks based pilot assignment[J]. Journal of Electronics &Information Technology, 2020, 42(10): 2454–2461. doi: 10.11999/JEIT190748 [16] 桂冠, 王禹, 黄浩. 基于深度学习的物理层无线通信技术: 机遇与挑战[J]. 通信学报, 2019, 40(2): 19–23. doi: 10.11959/j.issn.1000?436x.2019043GUI Guan, WANG Yu, and HUANG Hao. Deep learning based physical layer wireless communication techniques: Opportunities and challenges[J]. Journal on Communications, 2019, 40(2): 19–23. doi: 10.11959/j.issn.1000?436x.2019043 [17] HE Kaiming and SUN Jian. Convolutional neural networks at constrained time cost[C]. 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, USA, 2015. doi: 10.1109/CVPR.2015.7299173. [18] 盖建新, 薛宪峰, 吴静谊, 等. 基于深度卷积神经网络的协作频谱感知方法[J]. 电子与信息学报, 2021, 43(10): 2911–2919. doi: 10.11999/JEIT201005GAI Jianxin, XUE Xianfeng, WU Jingyi, et al. Cooperative spectrum sensing method based on deep convolutional neural network[J]. Journal of Electronics &Information Technology, 2021, 43(10): 2911–2919. doi: 10.11999/JEIT201005 -





 下载:
下载:








 下载:
下载:
