Ordered Escape Routing Combining Improved A* Algorithm with Rip-up and Reroute
-
摘要: 逃逸布线是印刷电路板设计的一个重要组成部分。针对并行逃逸布线的方法用于较大规模电路板布线时速度慢且结果不够好的问题,该文提出一种结合改进A*算法与拆线重布的有序逃逸布线方法。首先,通过代价预估函数确定引脚的布线顺序,使用改进A*算法初始化有序逃逸布线。接着,优化同长度布线路径,调整拥挤区域布线路径。最后,使用A*算法和广度优先搜索进行拆线重布。实验结果表明,该方法对给出的所有测试用例都实现了100%的逃逸,得到有序逃逸路径的可行解非常接近最优解,CPU时间比布尔可满足性问题(SAT)算法与最小费用多商品流(MMCF)算法平均减少分别约为95.6%, 97.8%,总体线长也接近最优。提出的方法能够明显减少寻找可行解的时间,提高布线质量。Abstract: Escape routing is an important part of the integrated circuit physical design. In order to solve the problem of slow parallel escape routing with unsatisfactory outcomes, an algorithm of ordered escape routing, combining the improved A* algorithm with the rip-up and reroute method is proposed. Firstly, the routing sequence of pins is determined by the cost estimation function and the improved A* algorithm is used to initialize the ordered escape routing. Secondly, the routing paths of the same length are optimized and the routing paths of the crowded areas are adjusted. Finally, A* algorithm and breadth-first search are employed to rip-up and reroute. The experimental results shows that this method achieved 100% escape routing for all given test cases, and that the feasible solution of the ordered escape paths is, to a great extent, close to the optimal solution. Compared to the Boolean Satisfiability Problem (SAT) algorithm and MMCF algorithm, this algorithm reduces CPU time by 95.6% and 97.8%, respectively, and makes the overall line length shorter. It is evident that the proposed method reduces the time required to find the feasible solution and optimize wire routing.
-
Key words:
- A* algorithm /
- Rip-up and reroute /
- Ordered escape routing /
- Shortest path
-
表 1 3种顺序选择方法结果对比
测试用例 方法1 方法2 方法3 总线长 布通率(%) 总线长 布通率(%) 总线长 布通率(%) Case5 52 92.0 52 92.0 50 92.0 Case6 46 86.6 60 93.3 57 93.3 Case7 255 80.0 259 82.2 276 88.8 Case8 419 91.4 429 92.8 471 97.1 平均 – 87.5 – 90.1 – 92.8 表 2 3种算法布线结果对比
测试用例 #Row #Col #Pin #Side #Cap 文献[13]SAT-based 文献[15]MMCF-based 本文方法 总线长 用时(s) 总线长 用时(s) 总线长 用时(s) Case1 8 6 6 1 1 21 0.07 21 0.05 21 0.002 Case2 8 8 8 2 1 24 0.07 24 0.09 24 0.001 Case3 8 8 10 2 1 39 0.26 39 0.15 39 0.003 Case4 8 8 10 3 1 36 0.66 36 1.34 36 0.003 Case5 10 6 25 3 1 *67 *0.14 *67 *0.58 67 0.027 Case6 10 10 15 4 1 62 1.57 62 3.36 62 0.011 Case7 20 15 45 2 1 326 2.02 338 10.24 326 0.251 Case8 30 30 70 4 1 – – *530 *30.15 489 0.032 Case9 8 10 31 2 2 – – 162 6.12 153 0.085 Case10 30 60 130 3 2 – – – – 2210 4.311 表 3 3个阶段布线结果对比
测试用例 阶段1 阶段2 阶段3 布通率(%) 总线长 用时(s) 布通率(%) 总线长 用时(s) 布通率(%) 总线长 用时(s) Case5 92.00 50 0.006 92.00 50 0.002 100 67 0.019 Case6 93.33 57 0.002 93.33 56 0.001 100 62 0.008 Case7 88.88 276 0.010 93.33 288 0.005 100 326 0.236 Case8 97.14 471 0.012 97.14 467 0.005 100 489 0.015 Case9 74.19 82 0.021 74.19 82 0.002 100 153 0.085 Case10 95.38 2048 0.192 95.38 2044 0.082 100 2210 4.037 -
[1] 徐宁, 洪先龙. 超大规模集成电路物理设计理论与算法[M]. 北京: 清华大学出版社, 2009: 147–172.XU Ning and HONG Xianlong. Very Large Scale Integration Physical Design Theory and Method[M]. Beijing: Tsinghua University Press, 2009: 147–172. [2] YAN Tan and WONG M D F. Recent research development in PCB layout[C]. 2010 IEEE/ACM International Conference on Computer-Aided Design (ICCAD'10), San Jose, USA, 2010: 398–403. doi: 10.1109/ICCAD.2010.5654190. [3] WANG Kan, WANG Huaxi, and DONG Sheqin. Escape routing of mixed-pattern signals based on staggered-pin-array PCBs[C]. 2013 ACM International Symposium on Physical Design, Stateline, United States, 2013: 93–100. doi: 10.1145/2451916.2451941. [4] FANG Jiawei, LIN I J, CHANG Y W, et al. A network-flow-based RDL routing algorithmz for flip-chip design[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2007, 26(8): 1417–1429. doi: 10.1109/TCAD.2007.891364 [5] MA Qiang, YOUNG E F Y, and WONG M D F. An optimal algorithm for layer assignment of bus escape routing on PCBs[C]. The 48th Design Automation Conference, San Diego, United States, 2011: 176–181. doi: 10.1145/2024724.2024764. [6] CHO B G, KAM D G, and KOO H I. Mixed-signal escape routing algorithm for multilayer PCBs[J]. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2019, 9(8): 1576–1586. doi: 10.1109/TCPMT.2019.2900463 [7] YAN Jintai. Direction-constrained rectangle escape routing[J]. ACM Transactions on Design Automation of Electronic Systems, 2018, 23(3): 34. doi: 10.1145/3178047 [8] ALPERT C J, MEHJTA D P, and SAPATNEKAR S S. Handbook of Algorithms for Physical Design Automation[M]. Boca Raton: CRC Press, 2008: 469–475. [9] TOMIOKA Y and TAKAHASHI A. Routing of monotonic parallel and orthogonal netlists for single-layer ball grid array packages[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2006, E89-A(12): 3551–3559. doi: 10.1093/ietfec/e89-a.12.3551 [10] FANG Jiawei, HSU C H, and CHANG Yaowen. An integer-linear-programming-based routing algorithm for flip-chip designs[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2009, 28(1): 98–110. doi: 10.1109/TCAD.2008.2009151 [11] LIAO Zhaopo and DONG Sheqin. A constraint-driven compact model with partition strategy for ordered escape routing[C]. 2020 on Great Lakes Symposium on VLSI, Virtual Event, New York, USA, 2020: 393–398. doi: 10.1145/3386263.3406942. [12] TOMIOKA Y and TAKAHASHI A. Monotonic parallel and orthogonal routing for single-layer ball grid array packages[C]. Proceedings of 2006 Asia and South Pacific Conference on Design Automation, Yokohama, Japan, 2006: 6–12. doi: 10.1109/ASPDAC.2006.1594758. [13] LUO Lijuan and WONG M D F. Ordered escape routing based on Boolean satisfiability[C]. 2008 Asia and South Pacific Design Automation Conference, Seoul, Korea (South), 2008: 244–249. doi: 10.1109/ASPDAC.2008.4483950. [14] LUO Lijuan and WONG M D F. On using SAT to ordered escape problems[C]. 2009 Asia and South Pacific Design Automation Conference, Yokohama, Japan, 2009: 594–599. doi: 10.1109/ASPDAC.2009.4796545. [15] JIAO Fengxian and DONG Sheqin. Ordered escape routing with consideration of differential pair and blockage[J]. ACM Transactions on Design Automation of Electronic Systems, 2018, 23(4): 46. doi: 10.1145/3185783 [16] 朱自然, 陈建利, 朱文兴. 基于多阶段拆线重布的总体布线算法[J]. 计算机辅助设计与图形学学报, 2016, 28(11): 2000–2008. doi: 10.3969/j.issn.1003-9775.2016.11.023ZHU Ziran, CHEN Jianli, and ZHU Wenxing. A global routing algorithm based on multistage rip-up and reroute[J]. Journal of Computer-Aided Design &Computer Graphics, 2016, 28(11): 2000–2008. doi: 10.3969/j.issn.1003-9775.2016.11.023 [17] SHI Rui and CHENQ C K. Efficient escape routing for hexagonal array of high density I/Os[C]. The 43rd Design Automation Conference, San Francisco, USA, 2006: 1003–1008. doi: 10.1109/DAC.2006.229424. [18] 赵奇, 赵阿群. 一种基于A*算法的多径寻由算法[J]. 电子与信息学报, 2013, 35(4): 952–957. doi: 10.3724/SP.J.1146.2012.00983ZHAO Qi and ZHAO Aqun. A multi-path routing algorithm base on A* algorithm[J]. Journal of Electronics &Information Technology, 2013, 35(4): 952–957. doi: 10.3724/SP.J.1146.2012.00983 [19] 高庆吉, 于咏生, 胡丹丹. 基于改进A*算法的可行性路径搜索及优化[J]. 中国民航学院学报, 2005, 23(4): 42–45. doi: 10.3969/j.issn.1001-5590.2005.04.010GAO Qingji, YU Yongsheng, and HU Dandan. Advanced A* algorithm for path-finding and optimization[J]. Journal of Civil Aviation University of China, 2005, 23(4): 42–45. doi: 10.3969/j.issn.1001-5590.2005.04.010 -





 下载:
下载:
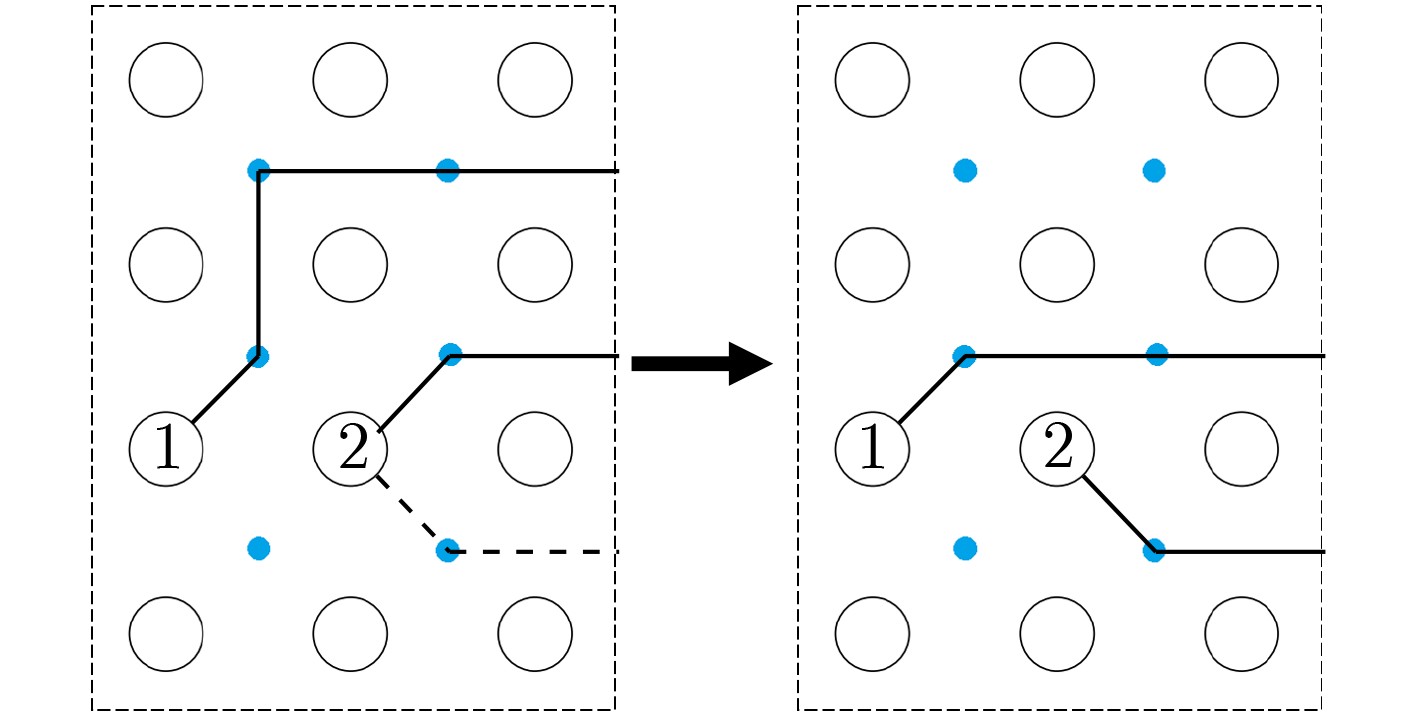
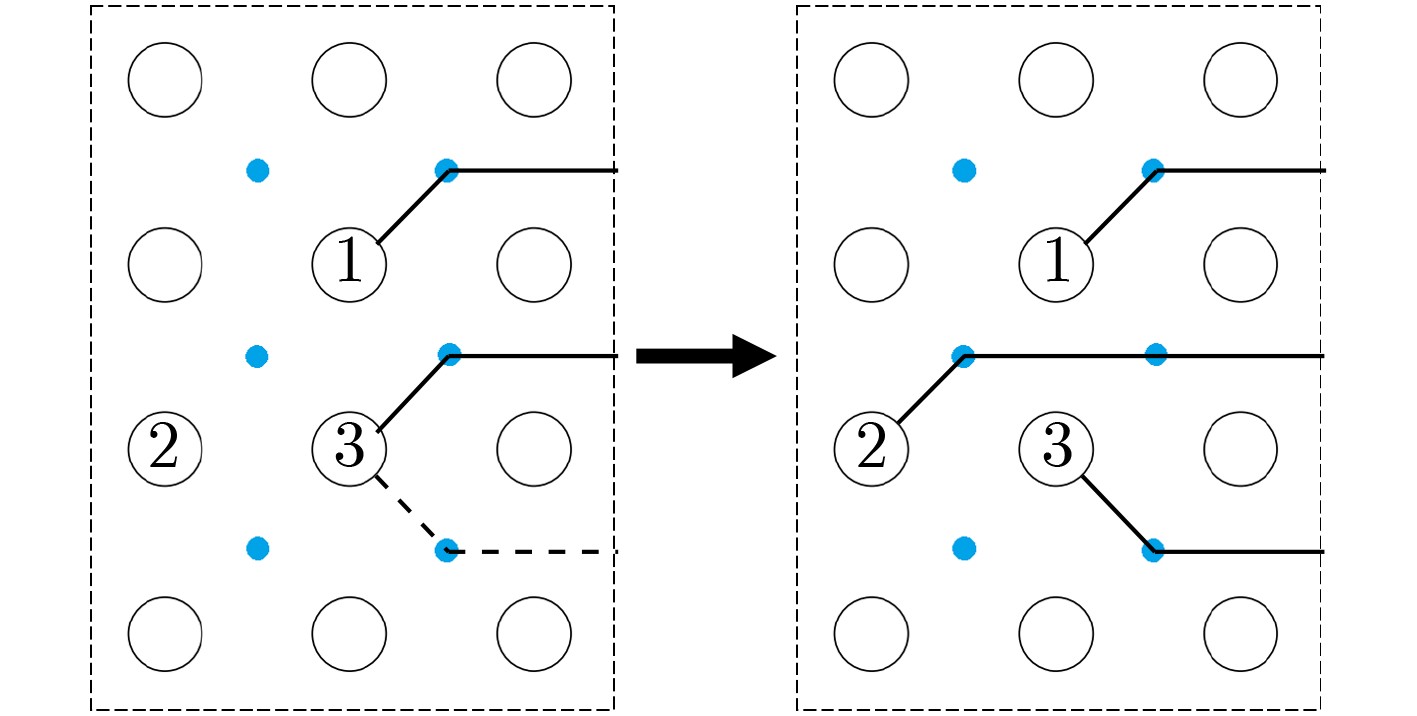




 下载:
下载:
