Over-The-Horizon Radar Target Tracking Based on Spatial Correlation Ionosphere Model
-
摘要: 天波超视距雷达(简称天波雷达)(OTHR)通过电离层反射效应可实现对多种高价值目标的远程预警。天波雷达目标跟踪算法设计中,电离层建模对其跟踪性能至关重要。该文考虑现实中电离层的空间相关性,提出一种基于高斯马尔可夫随机场(GMRF)的电离层虚高模型,以及相应的天波雷达多路径目标跟踪方法。该方法在贝叶斯估计的基础上,对多路径杂波环境下目标状态估计与电离层虚高参数进行联合建模与估计。该方法有效建立起了不同电离层区域之间的相关性,能够在电离层量测有限的情况下推断未量测区域的电离层虚高,改善电离层虚高参数辨识精度,进而提高目标跟踪精度。仿真结果表明基于空间相关性的电离层模型可以有效改善天波雷达目标跟踪性能。Abstract: Skywave Over-The-Horizon Radar (OTHR) relies on the earth’s ionosphere which reflects its electromagnetic waves to achieve long range early warning of a variety of high-value targets. The model of ionosphere is the key factor for OTHR target tracking. Considering the spatial correlation of the Virtual Ionospheric Height (VIH) in different geographic locations, a new VIH model, represented by a Gaussian Markov Random Field (GMRF) and a new multipath target tracking method are proposed. Based on Bayesian estimation, the new method estimates jointly target state and VIHs under multipath and clutter environment. Given the limited measurements of the ionospheric subregions, the VIHs of the unmeasured subregions are inferred based on the GMRF model, thereby the precision of VIHs and the accuracy of the target tracking are improved. Numerical simulation shows that the accuracy of OTHR target tracking is improved.
-
表 1 式(2)中传播模式与电离层参数的对应
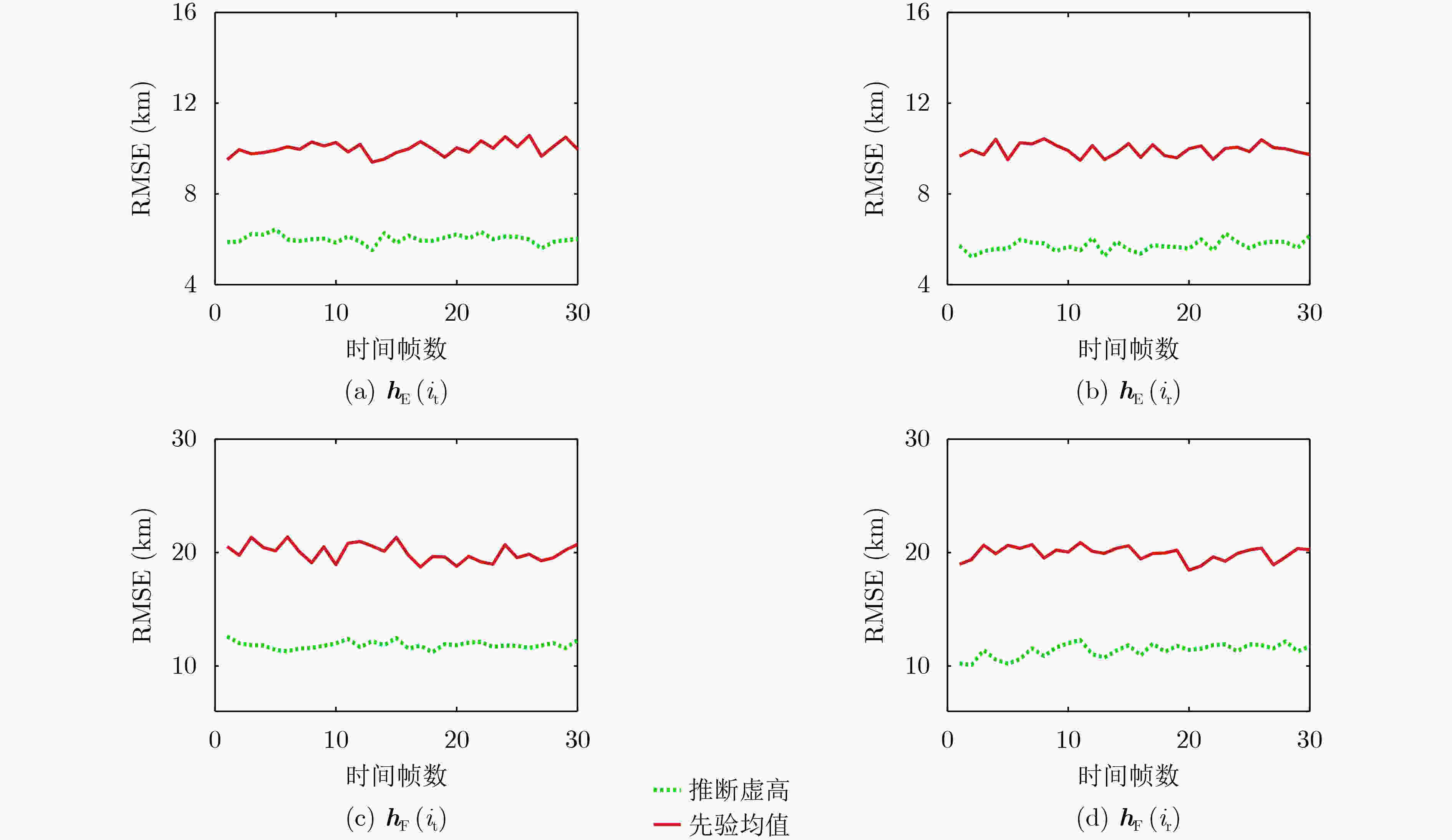
索引 模式 ${\theta _{\rm{t}}}$ ${\theta _{\rm{r}}}$ $m = 1$ EE ${ {\boldsymbol{h} }_{\rm{E} } }({i_{\rm{t}}})$ ${ {\boldsymbol{h} }_{\rm{E} } }({i_{\rm{r}}})$ $m = 2$ EF ${ {\boldsymbol{h} }_{\rm{E} } }({i_{\rm{t}}})$ ${ {\boldsymbol{h} }_{\rm{F} } }({i_{\rm{r}}})$ $m = 3$ FE ${ {\boldsymbol{h} }_{\rm{F} } }({i_{\rm{t}}})$ ${ {\boldsymbol{h} }_{\rm{E} } }({i_{\rm{r}}})$ $m = 4$ FF ${ {\boldsymbol{h} }_{\rm{F} } }({i_{\rm{t}}})$ ${ {\boldsymbol{h} }_{\rm{F} } }({i_{\rm{r}}})$ 表 2 量测预测及其协方差
输入:${{\boldsymbol{h}}_\beta }, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\boldsymbol{\mathcal{H}}_{\mathcal{D} \times \mathcal{N}}}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\boldsymbol{\hat x}_{k\mid k - 1}}$ 输出:$ {\boldsymbol{\widehat{y}}}_{k\mid k-1}^{m}, {\boldsymbol{S}}_{k}^{m}$ (1) 根据预测的目标状态估计${\boldsymbol{\hat x } _{k\mid k - 1}}$计算电离层子区域索引${i_{\rm{t}}}$和${i_{\rm{r}}}$, (2) 根据式(12)推断${{\boldsymbol{\hat h}}_{\alpha |\beta }}$和${\boldsymbol{\hat \Sigma } _{\alpha |\beta }}$, (3) for $m = 1, 2, 3, 4$ (4) 根据索引${i_{\rm{t}}}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {i_{\rm{r}}}{\kern 1pt}$、模式$m$和表1,在向量${[{({{\boldsymbol{\hat h}}_\alpha })^{\rm{T}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\boldsymbol{h}}_\beta ^{\rm{T}}]^{\rm{T}}}$中寻找
电离层虚高向量${\boldsymbol{\hat \theta } _k}$,(5) 根据索引${i_{\rm{t}}}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {i_{\rm{r}}}{\kern 1pt}$、模式$m$和表1,在向量$[{\kern 1pt} {({\rm{diag(} }{\boldsymbol{\hat \varSigma } _{\alpha |\beta } }{\rm{)} })^{\rm{T} } }$
${({\rm{diag(} }{\boldsymbol{\hat \varSigma } _{\beta \beta } }{\rm{)} })^{\rm{T} } }]^{\rm{T} }$中寻找协方差矩阵${{\boldsymbol{P}}_\theta }$的元素$\sigma ({\theta _{\rm{t}}})$和$\sigma ({\theta _{\rm{r}}})$,(6) 根据式(16)—式 (17),计算${\boldsymbol{\hat y}}_{k\mid k - 1}^m$和${\boldsymbol{S}}_k^m$ (7) end for 表 3 仿真场景参数设置
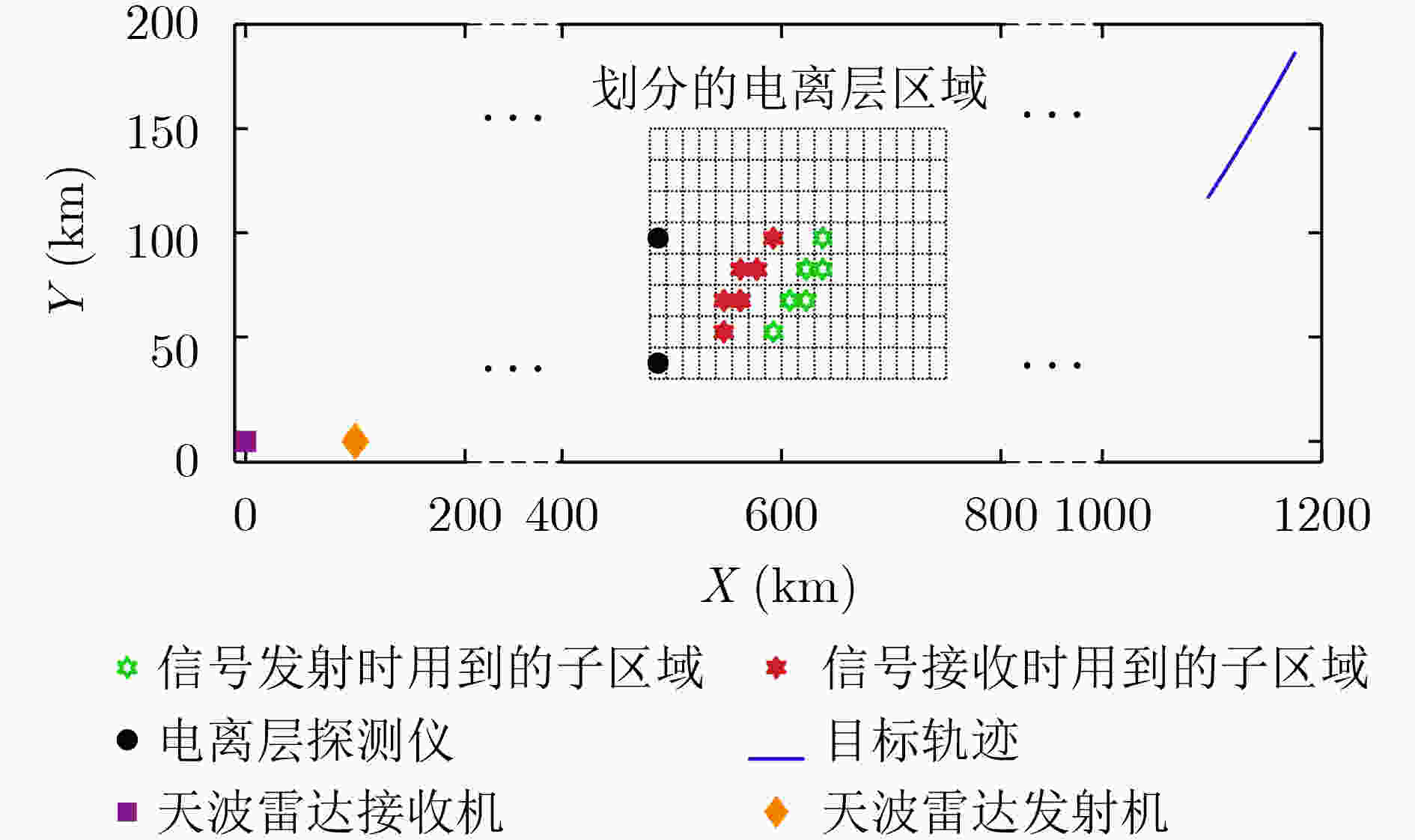
参数 值 参数 值 时间帧数总值 30 电离层区域(${\varDelta _X} \times {\varDelta _Y}$) 15 km×15 km 模式检测概率 0.7 每层子区域数目 144 每帧杂波期望 50 E层电离层虚高标准差 10 km 采样时间间隔(T) 20 s F层电离层虚高标准差 20 km 监视区域规模(径向距) 1000 km~1400 km ${{\boldsymbol{Q}}^{{\rm{E}}}}$对角线元素 0.082 监视区域规模(方位角) 4°~12° ${{\boldsymbol{Q}}^{{\rm{E}}}}$非对角线元素 –0.0205 电离层区域(X) 480 km~750 km ${{\boldsymbol{Q}}^{{\rm{F}}}}$对角线元素 0.0587 电离层区域(Y) 30 km~150 km ${{\boldsymbol{Q}}^{{\rm{F}}}}$非对角线元素 –0.0147 表 4 MPCR-GMRF, MPCR和MPDA的SSRSE对比
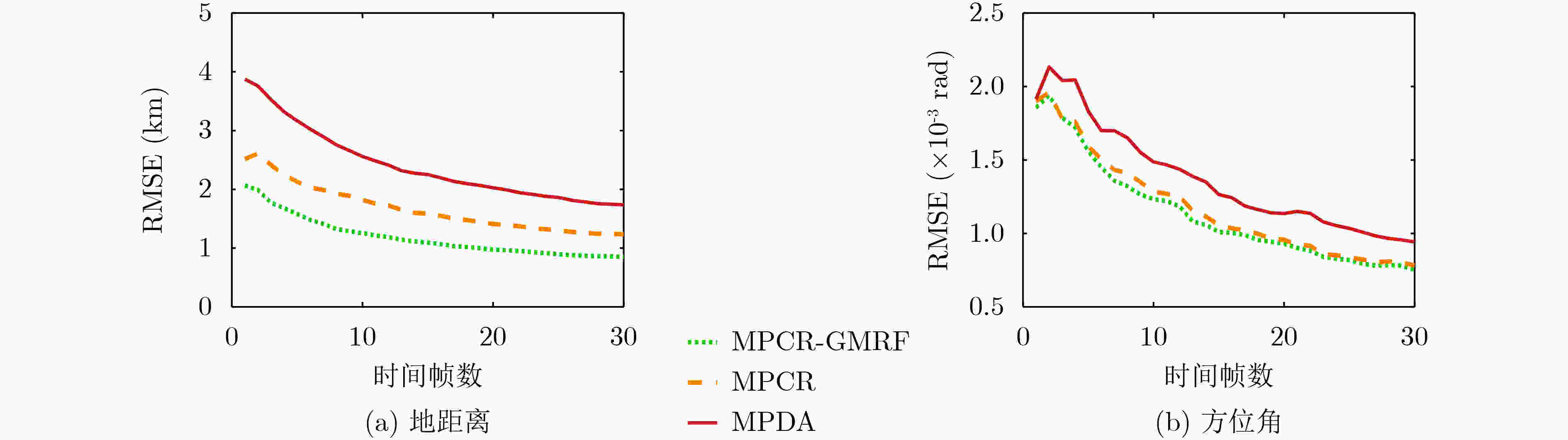
算法 径向距 径向距速率 方位角 MPCR-GMRF 6.06×10–4 0.003006 0.004326 MPCR 8.58×10–4 0.003115 0.004477 MPDA 12.26×10–4 0.003689 0.005416 -
[1] FABRIZIO G A. High Frequency Over-the-Horizon Radar: Fundamental Principles, Signal Processing, and Practical Applications[M]. New York: McGraw-Hill Education, 2013. [2] 周文瑜, 焦培南. 超视距雷达技术[M]. 北京: 电子工业出版社, 2008.ZHOU Wenyu and JIAO Peinan. Over-The-Horizon Radar[M]. Beijing: Publishing House of Electronics Industry, 2008. [3] PULFORD G W and EVANS R J. A multipath data association tracker for over-the-horizon radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(4): 1165–1183. doi: 10.1109/7.722704 [4] LAN Hua, LIANG Yan, PAN Quan, et al. An EM algorithm for multipath state estimation in OTHR target tracking[J]. IEEE Transactions on Signal Processing, 2014, 62(11): 2814–2826. doi: 10.1109/TSP.2014.2318134 [5] QIN Yong, MA Hong, CHEN Jinfeng, et al. Gaussian mixture probability hypothesis density filter for multipath multitarget tracking in over-the-horizon radar[J]. EURASIP Journal on Advances in Signal Processing, 2015, 2015: 108. doi: 10.1186/s13634-015-0294-y [6] TANG Xu, CHEN Xin, MCDONALD M, et al. A multiple-detection probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2015, 63(8): 2007–2019. doi: 10.1109/TSP.2015.2407322 [7] HUANG Yuan, SHI Yifang, and SONG T L. An efficient multi-path multitarget tracking algorithm for over-the-horizon radar[J]. Sensors, 2019, 19(6): 1384. doi: 10.3390/s19061384 [8] FENG Xiaoxue, LIANG Yan, ZHOU Lin, et al. Joint mode identification and localisation improvement of over-the-horizon radar with forward-based receivers[J]. IET Radar, Sonar & Navigation, 2014, 8(5): 490–500. doi: 10.1049/iet-rsn.2013.0017 [9] LAN Hua, LIANG Yan, WANG Zengfu, et al. Distributed ECM algorithm for OTHR multipath target tracking with unknown ionospheric heights[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 61–75. doi: 10.1109/JSTSP.2017.2787488 [10] RUTTEN M G and PERCIVAL D J. Joint ionospheric and target state estimation for multipath OTHR track fusion[C]. Signal and Data Processing of Small Targets 2001, San Diego, USA, 2001: 118–129. doi: 10.1117/12.492797. [11] LAN Hua, WANG Zhengfu, BAI Xianglong, et al. Measurement-level target tracking fusion for over-the-horizon radar network using message passing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(3): 1600–1623. doi: 10.1109/TAES.2020.3044109 [12] PULFORD G W. OTHR multipath tracking with uncertain coordinate registration[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(1): 38–56. doi: 10.1109/TAES.2004.1292141 [13] GENG Hang, LIANG Yan, and CHENG Yuhua. Target state and markovian jump ionospheric height bias estimation for OTHR tracking systems[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2020, 50(7): 2599–2611. doi: 10.1109/TSMC.2018.2822819 [14] GENG Hang, LIANG Yan, YANG Feng, et al. Joint estimation of target state and ionospheric height bias in over-the-horizon radar target tracking[J]. IET Radar, Sonar & Navigation, 2016, 10(7): 1153–1167. doi: 10.1049/iet-rsn.2015.0318 [15] SOICHER H. Spatial correlation of transionospheric signal time delays[J]. IEEE Transactions on Antennas and Propagation, 1978, 26(2): 311–314. doi: 10.1109/TAP.1978.1141826 [16] BUST G S, COKER C, COCO D S, et al. IRI data ingestion and ionospheric tomography[J]. Advances in Space Research, 2001, 27(1): 157–165. doi: 10.1016/S0273-1177(00)00163-0 [17] YUE Xinan, WAN W, LIU Libo, et al. Statistical analysis on spatial correlation of ionospheric day-to-day variability by using GPS and Incoherent Scatter Radar observations[J]. Annales Geophysicae, 2007, 25(8): 1815–1825. doi: 10.5194/angeo-25-1815-2007 [18] MINKWITZ D, VAN DEN BOOGAART K G, GERZEN T, et al. Tomography of the ionospheric electron density with geostatistical inversion[J]. Annales Geophysicae, 2015, 33(8): 1071–1079. doi: 10.5194/angeo-33-1071-2015 [19] NORBERG J, VIERINEN J, ROININEN L, et al. Gaussian Markov random field priors in ionospheric 3-D multi-instrument tomography[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(12): 7009–7021. doi: 10.1109/TGRS.2018.2847026 [20] NORBERG J, ROININEN L, VIERINEN J, et al. Ionospheric tomography in Bayesian framework with Gaussian Markov random field priors[J]. Radio Science, 2015, 50(2): 138–152. doi: 10.1002/2014RS005431 [21] BOOKER H G and SEATON S L. Relation between actual and virtual ionospheric height[J]. Physical Review, 1940, 57(2): 87–94. doi: 10.1103/PhysRev.57.87 [22] WHEADON N S, WHITEHOUSE J C, MILSOM J D, et al. Ionospheric modelling and target coordinate registration for HF sky-wave radars[C]. 1994 Sixth International Conference on HF Radio Systems and Techniques, York, UK, 1994: 258-266. doi: 10.1049/cp:19940504. [23] LI S Z. Markov Random Field Modeling in Image Analysis[M]. London: Springer Science & Business Media, 2009. [24] RUE H and HELD L. Gaussian Markov Random Fields. Theory and Applications[M]. Boca Raton: Chapman & Hall/CRC, 2005. -





 下载:
下载:


 下载:
下载:
