自适应空间异常的目标跟踪

姜文涛; 刘晓璇; 涂潮; 金岩

doi:10.11999/JEIT201025

自适应空间异常的目标跟踪

doi: 10.11999/JEIT201025

辽宁工程技术大学软件学院葫芦岛 125105

基金项目: 国家自然科学基金(61172144)，辽宁省自然科学基金(20170540426)，辽宁省教育厅基金(LJYL049)

详细信息

作者简介:
姜文涛：男，1986年生，副教授，研究方向为图像与视觉计算、模式识别与人工智能

刘晓璇：女，1996年生，硕士生，研究方向为图像与视觉计算、模式识别与人工智能

涂潮：男，1993年生，硕士生，研究方向为图像与视觉计算、模式识别与人工智能

金岩：男，1996年生，硕士生，研究方向为图像与视觉计算、模式识别与人工智能

通讯作者:
刘晓璇　1481167384@qq.com

中图分类号: TN911.73; TP391.4
计量
- 文章访问数: 984
- HTML全文浏览量: 592
- PDF下载量: 118
- 被引次数: 0
出版历程
- 收稿日期: 2020-12-07
- 修回日期: 2021-08-14
- 网络出版日期: 2021-09-15
- 刊出日期: 2022-02-25

Adaptive Spatial and Anomaly Target Tracking

School of Software, Liaoning Technical University, Huludao 125105, China

Funds: The National Natural Science Foundation of China (61172144), The National Natural Science Foundation of Liaoning Province (20170540426), The Foundation of Education Department of Liaoning Province (LJYL049)

摘要

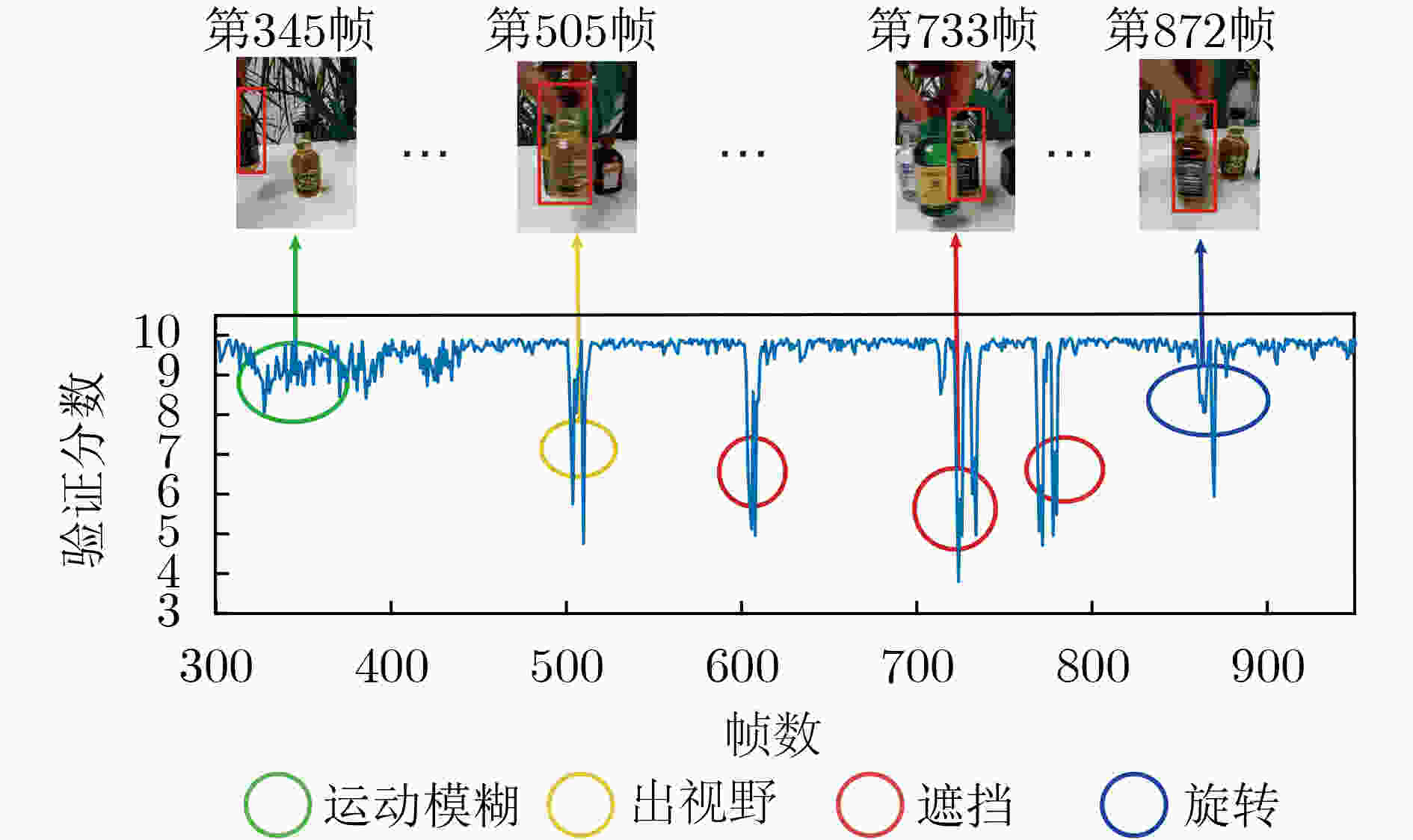
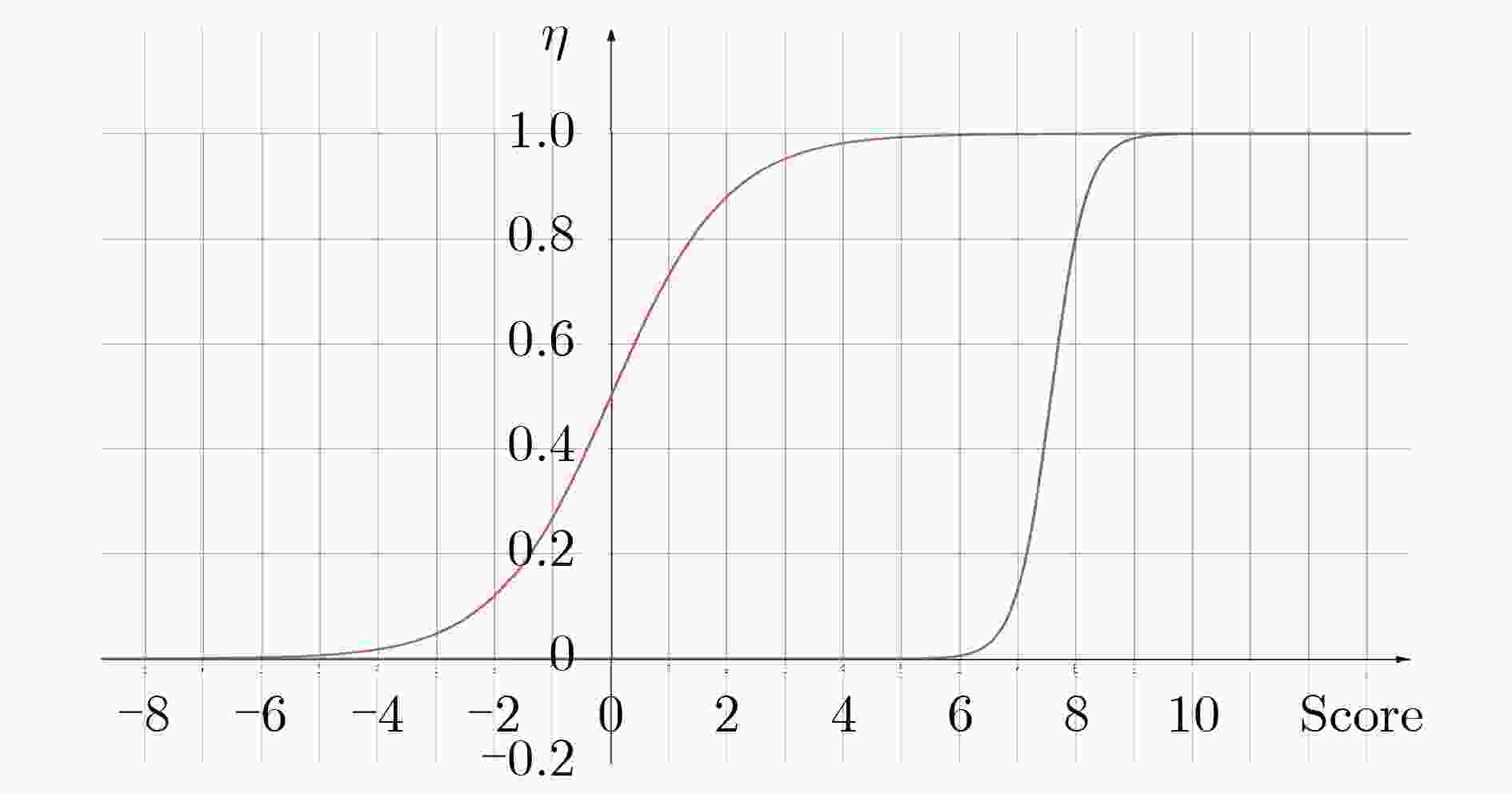
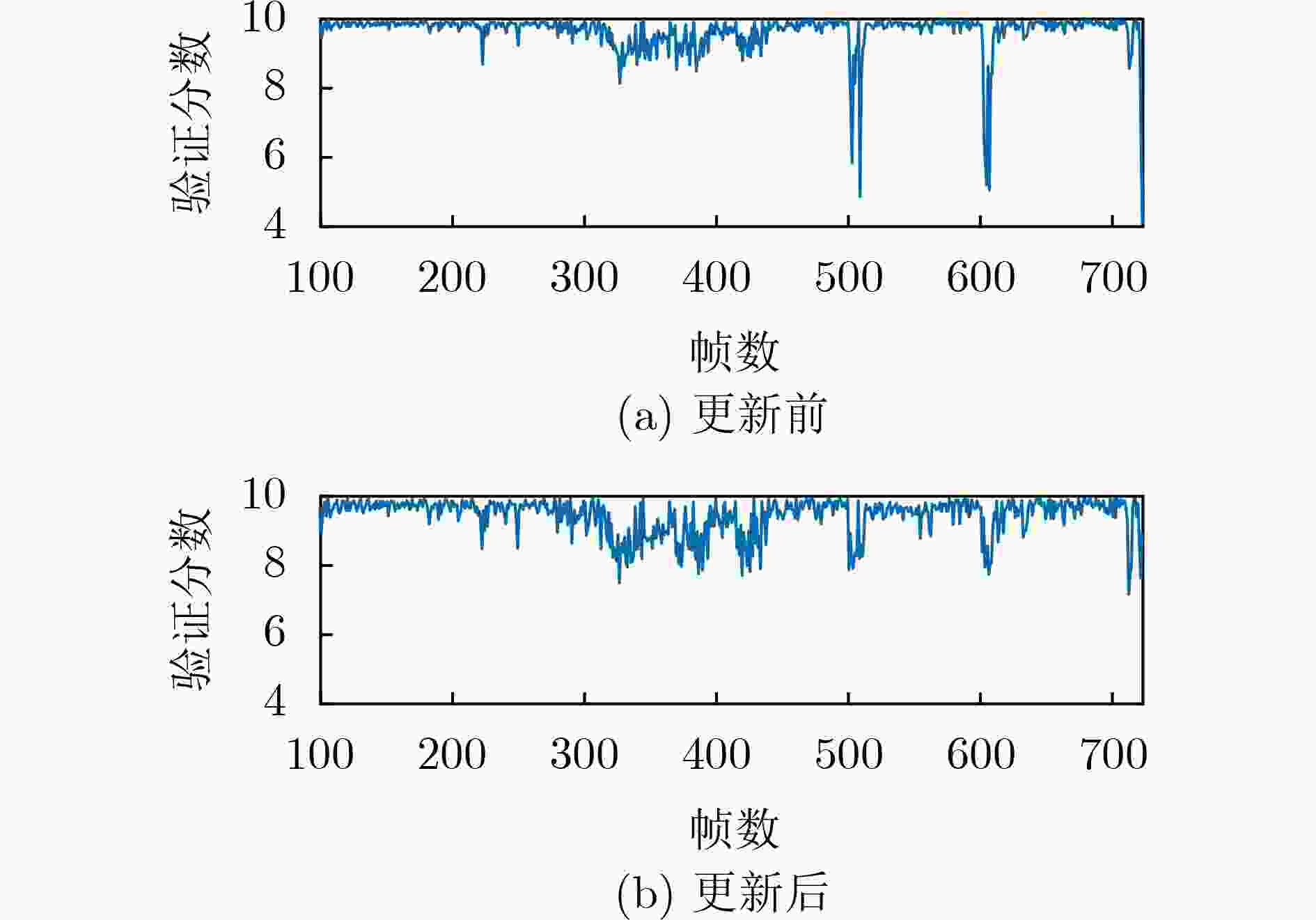
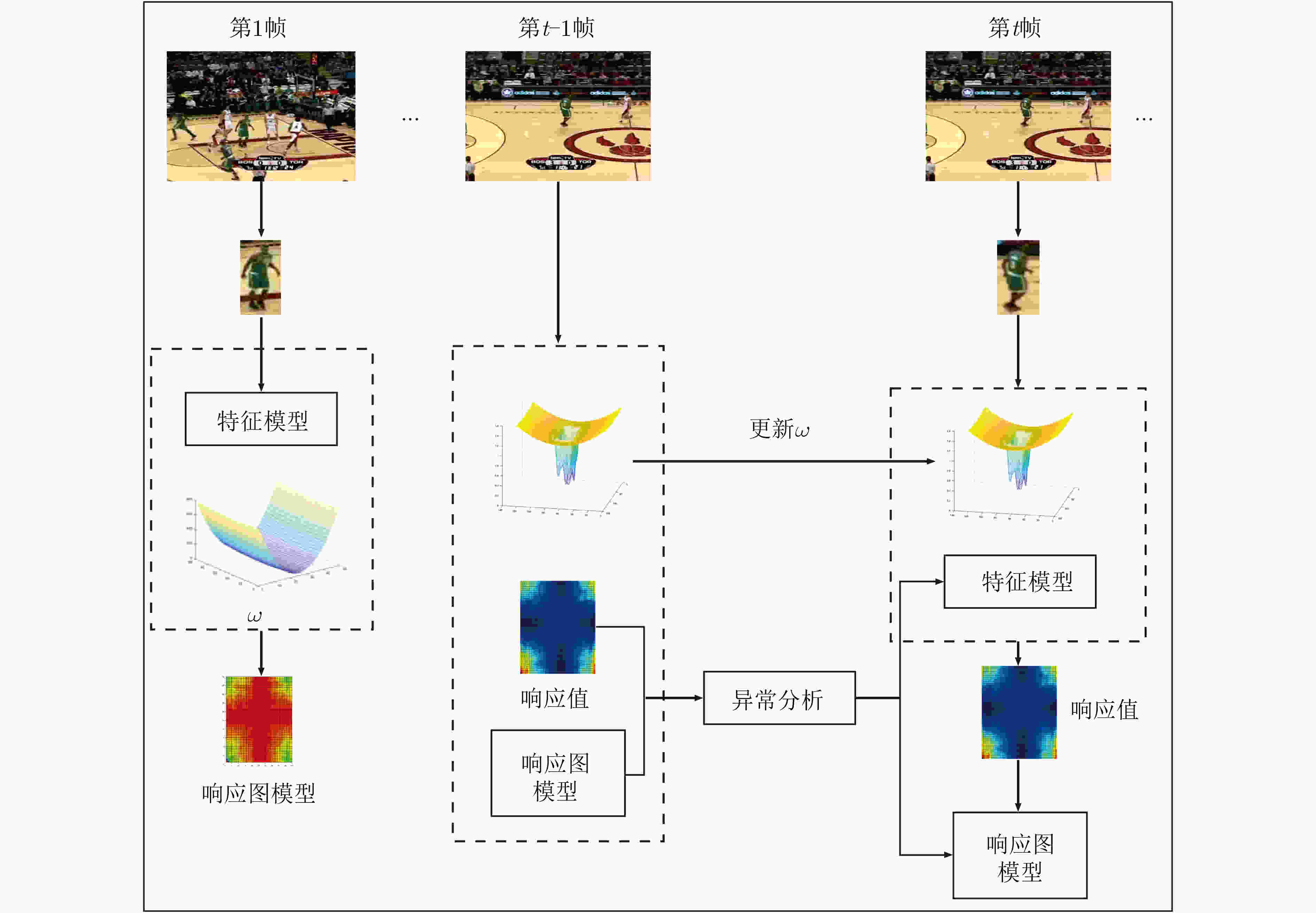
摘要: 为了解决判别式空间正则项的目标跟踪算法在遮挡、旋转等因素干扰下失跟率较高的问题，该文提出一种自适应空间异常的目标跟踪算法。首先，在目标函数中加入自适应空间正则项，既缓解了边界效应带来的影响，又提高了滤波器对目标和背景区域的分辨能力；其次，根据每一帧的响应值计算验证分数，分析跟踪结果的可信度和异常情况；最后为目标模型和响应图模型的更新速率实现动态取值。大量实验结果表明，自适应空间异常的目标跟踪算法能够较好地处理背景模糊、形状变化等多种异常情况，具有较高的跟踪性能。
- 目标跟踪 /
- 自适应空间正则项 /
- 异常分析 /
- 动态更新
Abstract: In order to solve the problem that the target tracking algorithm based on the discriminant spatial regularization term has a high mistracking rate under the interference of occlusion, rotation and other factors, an adaptive spatial and anomaly target tracking is proposed. Firstly, an adaptive spatial regularization term is constructed in the objective function, which not only alleviates the influence of boundary effect, but also improves the resolution of the filter between the target and the background region. Secondly, the verification score is calculated according to the response value of each frame, and the reliability and abnormality of the tracking results are analyzed. Finally, the updating rate of target model and response model is dynamically evaluated. A large number of experimental results show that the target tracking algorithm based on adaptive spatial anomaly can deal with background blur, shape change and other abnormal situations well, and has robust tracking performance.
- Target tracking /
- Adaptive space regular term /
- Anomaly analysis /
- Dynamic update

HTML全文

图 1 视频序列异常分析示意图

下载: 全尺寸图片幻灯片

图 2 参数取值示意图

下载: 全尺寸图片幻灯片

图 3 自适应模型更新前后的验证分数曲线

下载: 全尺寸图片幻灯片

图 4 总体框架图

下载: 全尺寸图片幻灯片

图 5 各种算法在部分序列上的跟踪结果对比

下载: 全尺寸图片幻灯片

图 6 各种算法在数据集OTB100上的对比曲线

下载: 全尺寸图片幻灯片

表 1 各种跟踪算法在数据集OTB100上各种属性的精确率得分

	本文	STRCF	SRDCF	Staple	BACF	ECO	ARCF	ASRCF	AutoTrack
光照变化	0.840	0.835	0.754	0.775	0.824	0.800	0.768	0.777	0.776
尺度变化	0.865	0.838	0.736	0.721	0.769	0.757	0.727	0.731	0.744
遮挡	0.858	0.812	0.726	0.724	0.740	0.720	0.683	0.691	0.713
形变	0.847	0.839	0.712	0.747	0.773	0.765	0.745	0.756	0.743
运动模糊	0.857	0.822	0.741	0.692	0.761	0.736	0.735	0.728	0.766
快速运动	0.843	0.803	0.763	0.710	0.807	0.789	0.745	0.733	0.770
平面内旋转	0.835	0.813	0.721	0.767	0.796	0.781	0.725	0.736	0.774
平面外旋转	0.878	0.848	0.725	0.736	0.785	0.767	0.723	0.755	0.751
超视野	0.832	0.771	0.621	0.668	0.765	0.748	0.671	0.677	0.723
复杂背景	0.854	0.875	0.738	0.748	0.830	0.800	0.787	0.761	0.758
低分辨率	0.810	0.746	0.631	0.610	0.739	0.741	0.707	0.582	0.764

下载: 导出CSV

表 2 各种跟踪算法在数据集OTB100上各种属性的成功率得分

	本文	STRCF	SRDCF	Staple	BACF	ECO	ARCF	ASRCF	AutoTrack
光照变化	0.802	0.797	0.697	0.708	0.797	0.776	0.749	0.749	0.746
尺度变化	0.815	0.750	0.650	0.596	0.695	0.689	0.646	0.689	0.648
遮挡	0.822	0.763	0.670	0.653	0.707	0.689	0.652	0.687	0.661
形变	0.788	0.744	0.640	0.656	0.705	0.693	0.694	0.715	0.686
运动模糊	0.840	0.784	0.708	0.639	0.734	0.727	0.711	0.711	0.731
快速运动	0.815	0.747	0.710	0.645	0.766	0.760	0.709	0.709	0.718
平面内旋转	0.792	0.730	0.630	0.668	0.714	0.704	0.651	0.686	0.667
平面外旋转	0.839	0.774	0.635	0.643	0.718	0.697	0.650	0.715	0.663
超视野	0.771	0.695	0.561	0.548	0.694	0.689	0.638	0.671	0.655
复杂背景	0.805	0.826	0.660	0.687	0.796	0.766	0.771	0.754	0.702
低分辨率	0.734	0.659	0.562	0.472	0.664	0.663	0.637	0.560	0.668

下载: 导出CSV

表 3 各种跟踪算法在数据集OTB100上平均跟踪速度(帧/s)

本文	STRCF	SRDCF	Staple	BACF	ECO	ARCF	ASRCF	AutoTrack
14.9	13.3	3.9	61.4	16.9	27.9	12.6	19.8	16.2

下载: 导出CSV

参考文献(22)

[1]	卢湖川, 李佩霞, 王栋. 目标跟踪算法综述[J]. 模式识别与人工智能, 2018, 31(1): 61–67. doi: 10.16451/j.cnki.issn1003-6059.201801006 LU Huchuan, LI Peixia, and WANG Dong. Visual object tracking: A survey[J]. Pattern Recognition and Artificial Intelligence, 2018, 31(1): 61–67. doi: 10.16451/j.cnki.issn1003-6059.201801006
[2]	葛宝义, 左宪章, 胡永江. 视觉目标跟踪方法研究综述[J]. 中国图象图形学报, 2018, 23(8): 1091–1107. doi: 10.11834/jig.170604 GE Baoyi, ZUO Xianzhang, and HU Yongjiang. Review of visual object tracking technology[J]. Journal of Image and Graphics, 2018, 23(8): 1091–1107. doi: 10.11834/jig.170604
[3]	孟琭, 杨旭. 目标跟踪算法综述[J]. 自动化学报, 2019, 45(7): 1244–1260. doi: 10.16383/j.aas.c180277 MENG Lu and YANG Xu. A survey of object tracking algorithms[J]. Acta Automatica Sinica, 2019, 45(7): 1244–1260. doi: 10.16383/j.aas.c180277
[4]	段建民, 马学峥, 柳新. 基于MFAPC的无人驾驶汽车路径跟踪方法[J]. 计算机工程, 2019, 45(6): 6–11, 20. doi: 10.19678/j.issn.1000-3428.0052439 DUAN Jianmin, MA Xuezheng, and LIU Xin. Path tracking method of unmanned vehicle based on MFAPC[J]. Computer Engineering, 2019, 45(6): 6–11, 20. doi: 10.19678/j.issn.1000-3428.0052439
[5]	姜文涛, 刘万军, 袁姮. 基于软特征理论的目标跟踪研究[J]. 计算机学报, 2016, 39(7): 1334–1355. doi: 10.11897/SP.J.1016.2016.01334 JIANG Wentao, LIU Wanjun, and YUAN Heng. Research of object tracking based on soft feature theory[J]. Chinese Journal of Computers, 2016, 39(7): 1334–1355. doi: 10.11897/SP.J.1016.2016.01334
[6]	李娜, 吴玲风, 李大湘. 基于相关滤波的长期跟踪算法[J]. 模式识别与人工智能, 2018, 31(10): 899–908. doi: 10.16451/j.cnki.issn1003-6059.201810004 LI Na, WU Lingfeng, and LI Daxiang. Long-term tracking algorithm based on correlation filter[J]. Pattern Recognition and Artificial Intelligence, 2018, 31(10): 899–908. doi: 10.16451/j.cnki.issn1003-6059.201810004
[7]	刘万军, 孙虎, 姜文涛. 自适应特征选择的相关滤波跟踪算法[J]. 光学学报, 2019, 39(6): 0615004. doi: 10.3788/AOS201939.0615004 LIU Wanjun, SUN Hu, and JIANG Wentao. Correlation filter tracking algorithm for adaptive feature selection[J]. Acta Optica Sinica, 2019, 39(6): 0615004. doi: 10.3788/AOS201939.0615004
[8]	姜文涛, 涂潮, 刘万军. 背景与方向感知的相关滤波跟踪[J]. 中国图象图形学报, 2021, 26(3): 527–541. doi: 10.11834/jig.200139 JIANG Wentao, TU Chao, and LIU Wanjun. Background and direction-aware correlation filter tracking[J]. Journal of Image and Graphics, 2021, 26(3): 527–541. doi: 10.11834/jig.200139
[9]	BOLME D S, BEVERIDGE J R, DRAPER B A, et al. Visual object tracking using adaptive correlation filters[C]. 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, USA, 2010: 2544–2550. doi: 10.1109/CVPR.2010.5539960.
[10]	HENRIQUES J F, CASEIRO R, MARTINS P, et al. Exploiting the circulant structure of tracking-by-detection with kernels[C]. The 12th European Conference on Computer Vision, Florence, Italy, 2012: 702–715. doi: 10.1007/978-3-642-33765-9_50.
[11]	HENRIQUES J F, CASEIRO R, MARTINS P, et al. High-speed tracking with kernelized correlation filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583–596. doi: 10.1109/TPAMI.2014.2345390
[12]	DANELLJAN M, HÄGER G, KHAN F M, et al. Learning spatially regularized correlation filters for visual tracking[C]. IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 2015: 4310–4318. doi: 10.1109/ICCV.2015.490.
[13]	GALOOGAHI H K, SIM T, and LUCEY S. Correlation filters with limited boundaries[C]. IEEE Conference on Computer Vision and Pattern Recognition, Boston, USA, 2015: 4630–4638. doi: 10.1109/CVPR.2015.7299094.
[14]	GALOOGAHI H K, FAGG A, and LUCEY S. Learning background-aware correlation filters for visual tracking[C]. Proceeding of 2017 IEEE International Conference on Computer Vision, Venice, Italy, 2017: 1144–1152. doi: 10.1109/ICCV.2017.129.
[15]	LI Feng, TIAN Cheng, ZUO Wangmeng, et al. Learning spatial-temporal regularized correlation filters for visual tracking[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 4904–4913. doi: 10.1109/CVPR.2018.00515.
[16]	DAI Ke’nan, WANG Dong, LU Huchuan, et al. Visual tracking via adaptive spatially-regularized correlation filters[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, USA, 2019: 4665–4674. doi: 10.1109/CVPR.2019.00480.
[17]	LI Yiming, FU Changhong, DING Fangqiang, et al. AutoTrack: Towards high-performance visual tracking for UAV with automatic spatio-temporal regularization[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, USA, 2020: 11920–11929. doi: 10.1109/CVPR42600.2020.01194.
[18]	HUANG Ziyuan, FU Changhong, LI Yiming, et al. Learning aberrance repressed correlation filters for real-time UAV tracking[C]. IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea (South), 2019: 2891–2900. doi: 10.1109/ICCV.2019.00298.
[19]	BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends ^® in Machine Learning, 2010, 3(1): 1–122. doi: 10.1561/2200000016
[20]	马燕青. 求解约束优化问题的增广拉格朗日函数法[D]. [硕士论文], 重庆师范大学, 2013. MA Yanqing. Augmented lagrangian function methods for solving constrained optimization problems[D]. [Master dissertation], Chongqing Normal University, 2013.
[21]	BERTINETTO L, VALMADRE J, GOLODETZ S, et al. Staple: Complementary learners for real-time tracking[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 1401–1409. doi: 10.1109/CVPR.2016.156.
[22]	DANELLJAN M, BHAT G, KHAN F S, et al. ECO: Efficient convolution operators for tracking[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 6931–6939. doi: 10.1109/CVPR.2017.733.