Joint Design of Millimeter-wave Radar Waveform Parameters and Receiving Weight under Resolution Constraints
-
摘要: 针对自动驾驶中有限平台空间及发射功率导致毫米波雷达目标检测性能较低的问题,该文提出一种距离及速度分辨率约束下提升毫米波雷达目标检测概率的波形参数及接收权联合设计方法。首先,基于调频连续波(FMCW)信号,所提方法建立了毫米波相控阵阵列检测模型;其次,通过分析距离及速度分辨率与发射波形参数关系,构建考虑距离及速度分辨率的发射波形参数约束;然后,基于最大化输出信杂噪比(SCNR)准则,建立具有距离及速度分辨率约束的发射波形参数及接收权值联合优化模型以改善毫米波雷达目标检测及距离速度分辨性能;最后,所提方法基于交替迭代方法求解所得复杂非线性优化问题。仿真结果表明,所提方法可自适应调整发射波形参数和接收权以提升目标检测性能同时满足距离及速度分辨率需求。Abstract: Considering the issue of poor target detection performance of millimeter-wave radar caused by the limited platform space and transmitting power in the case of autonomous driving, a joint design approach of waveform parameters and receiving weight is developed in this paper to improve the target detection probability of millimeter wave radar with range and velocity resolution constraints. Firstly, based on the Frequency Modulated Continuous Wave (FMCW) signal, the millimeter-wave phased array detection model is established via the proposed method; Secondly, the constraints of the transmitting waveform parameters concerning the range and velocity resolution are constructed by analyzing the relationship between the range along with speed resolution and the transmitting waveform parameters; After that, based on the criterion of maximizing the output Signal to Clutter plus Noise Ratio (SCNR), a joint optimization model of transmitting waveform parameters and receiving weight with range and velocity resolution constraints is established to improve the target detection and range-velocity resolution performance of millimeter wave radar; Finally, based on the alternate iteration method, the resultant complex nonlinear optimization problem can be solved via the developed approach. Simulation results show that the proposed method can adaptively adjust the transmitting waveform parameters and receiving weight to improve the target detection performance with satisfying the requirements of range and speed resolution.
-
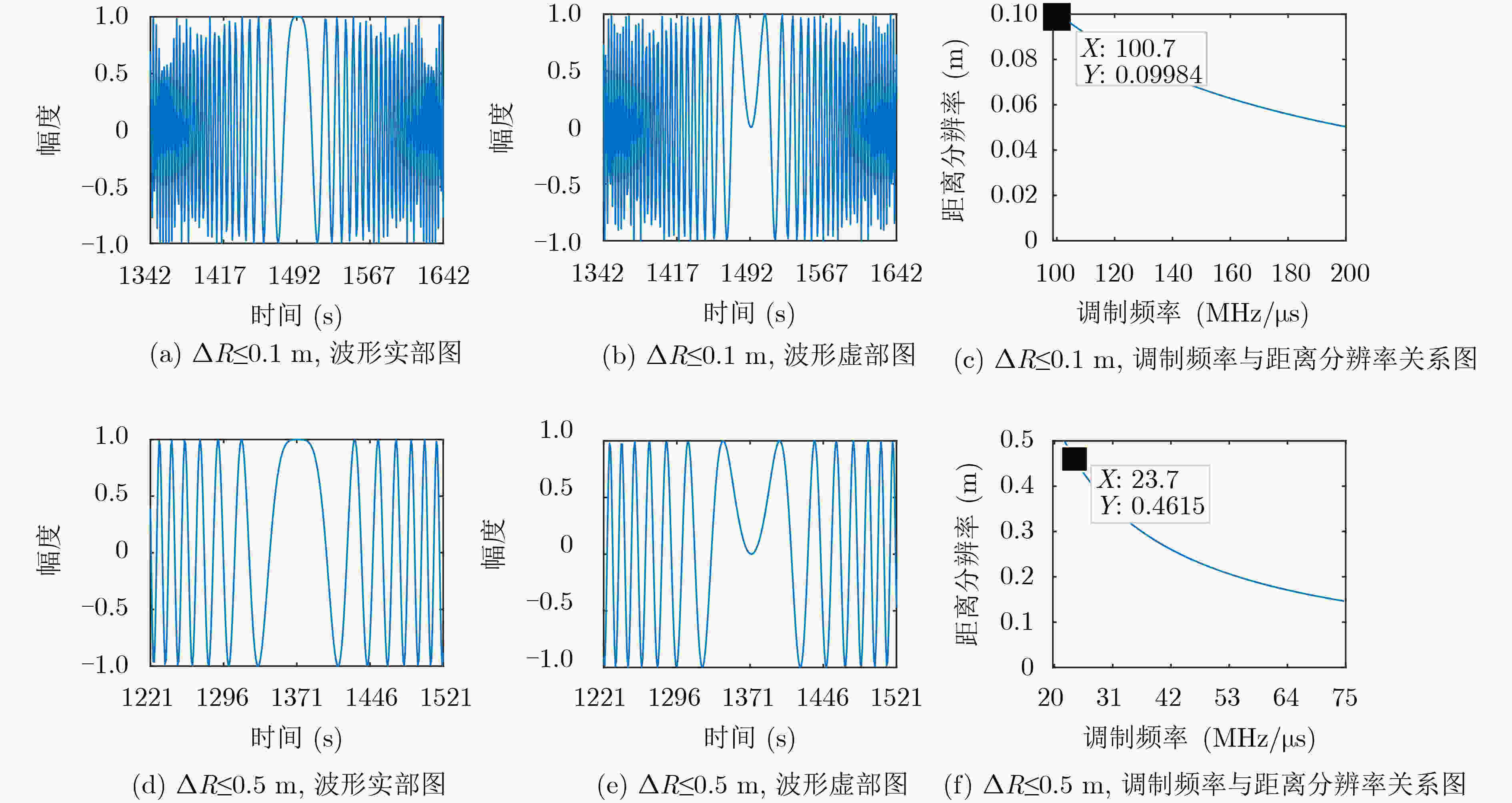
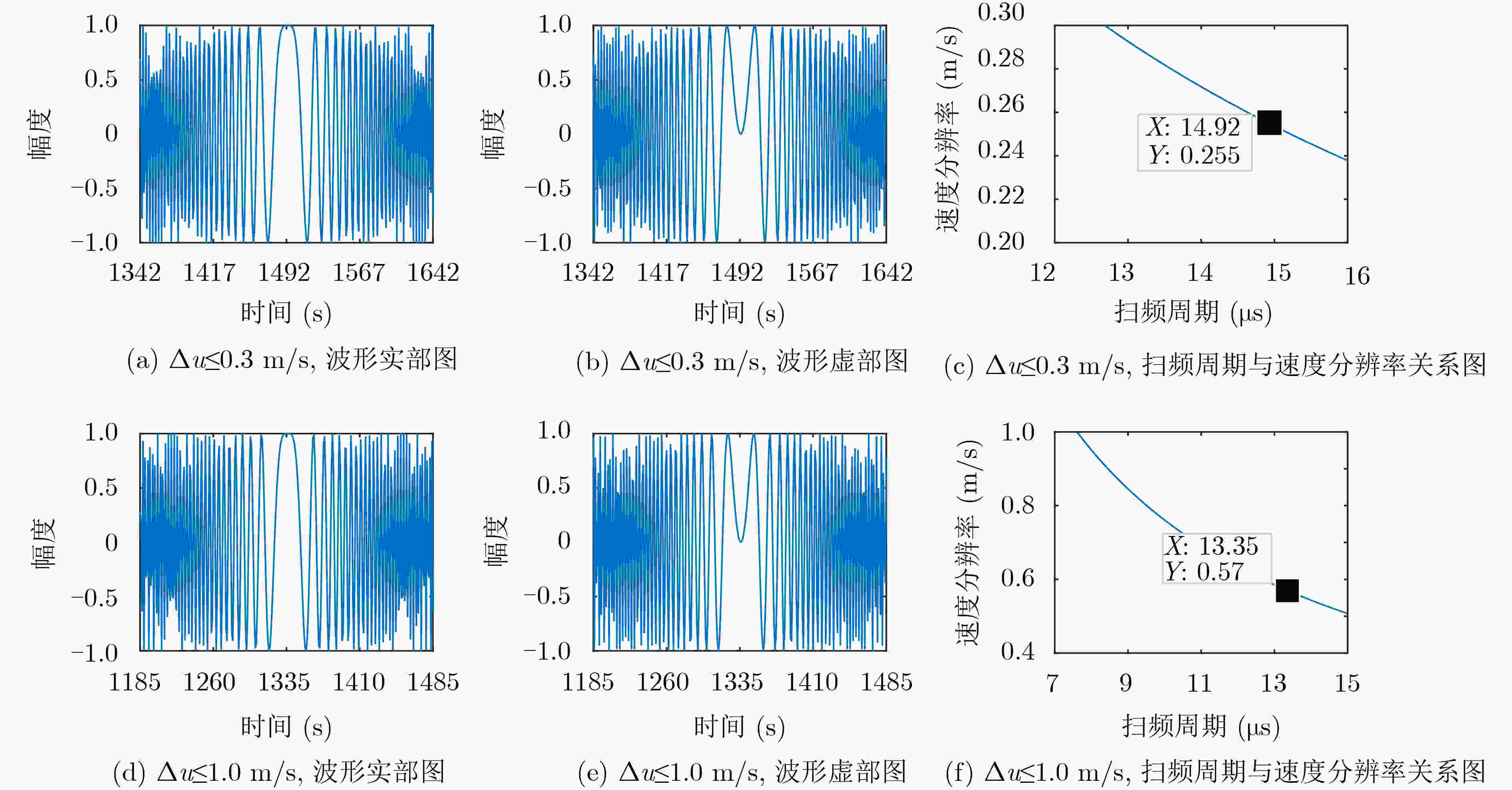
表 1 远近距离下雷达参数设置
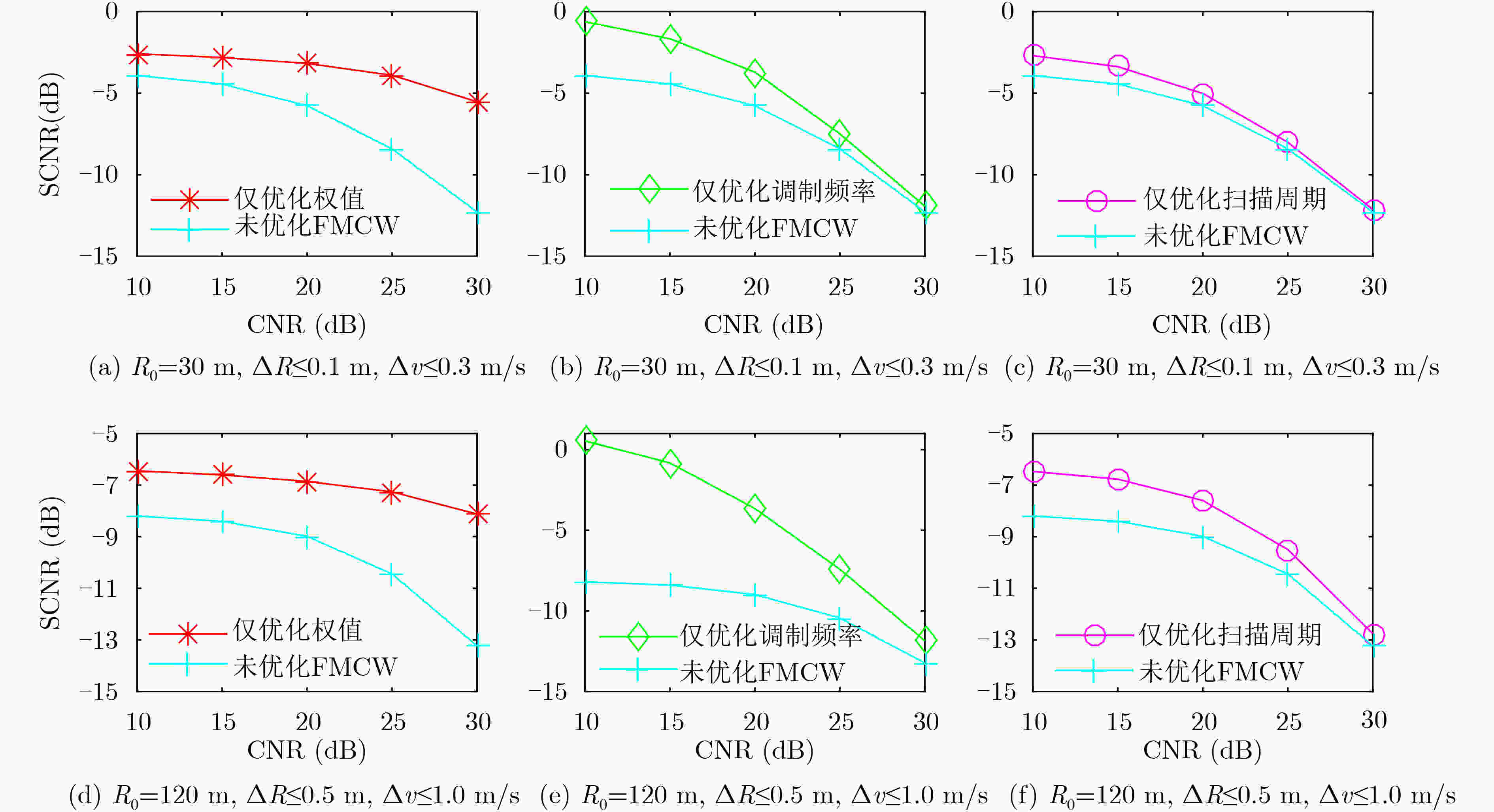
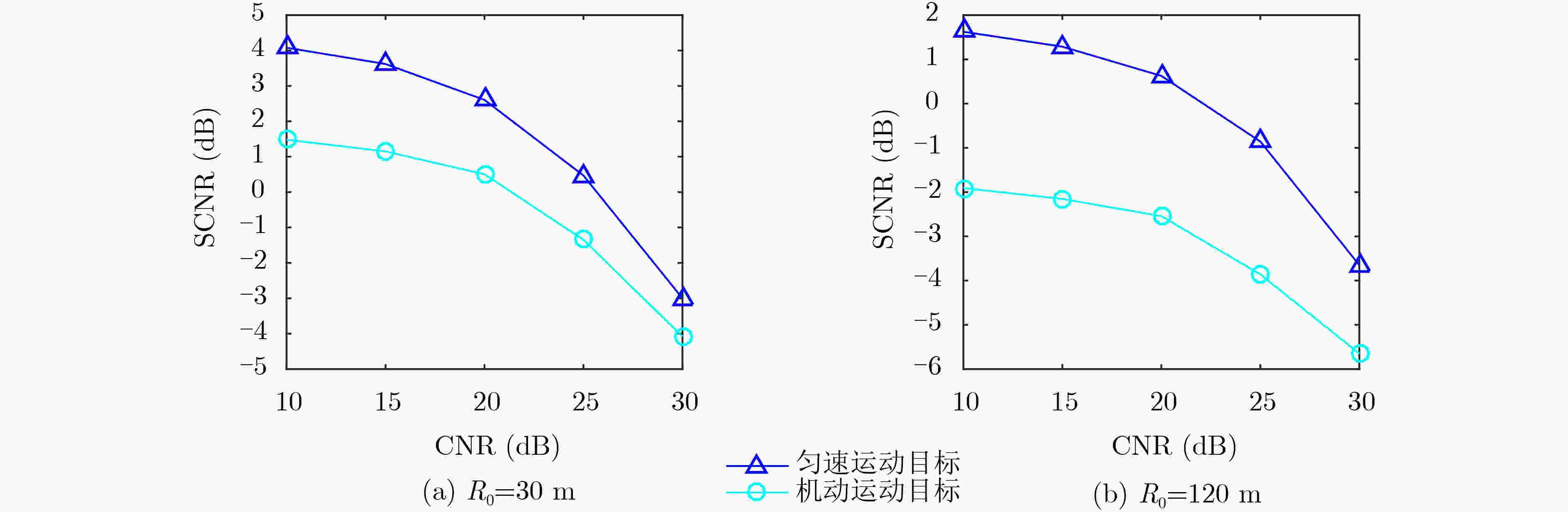
目标初始距离${R_0}{\rm{(m)}}$ 距离分辨率$\Delta R({\rm{m)}}$ 速度分辨率$\Delta v({\rm{m/s}})$ 最大可检测距离${R_{\max }}({\rm{m)}}$ 扫频周期数$L$ $0 < {R_0} < 75$ $\Delta R \le 0.1$ $\Delta v \le 0.3$ $75$ $512$ $75 \le {R_0} \le 200$ $\Delta R \le 0.5$ $\Delta v \le 1.0$ $200$ $256$ -
[1] ZHANG Cheng, CAO Mengde, GONG Yuqin, et al. Calibration of motional frequency spread for wide-band FMCW automotive millimeter-wave radar[J]. IEEE Access, 2020, 8: 14355–14366. doi: 10.1109/ACCESS.2020.2966222 [2] LI Xin, TAO Xiaowen, ZHU Bing, et al. Research on a simulation method of the millimeter wave radar virtual test environment for intelligent driving[J]. Sensors, 2020, 20(7): 1929. doi: 10.3390/s20071929 [3] ZHANG Xiaowen, WANG Kaizhi, and LIU Xingzhao. Adaptive waveform optimization design for target detection in cognitive radar[J]. Journal of Applied Remote Sensing, 2017, 11(1): 015024. doi: 10.1117/1.JRS.11.015024 [4] XU Huaping, ZHANG Jiawei, LIU Wei, et al. High-resolution radar waveform design based on target information maximization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(5): 3577–3587. doi: 10.1109/TAES.2020.2976085 [5] BILIK I, LONGMAN O, VILLEVAL S, et al. The rise of radar for autonomous vehicles: Signal processing solutions and future research directions[J]. IEEE Signal Processing Magazine, 2019, 36(5): 20–31. doi: 10.1109/MSP.2019.2926573 [6] STOVE A G. Linear FMCW radar techniques[J]. IEE Proceedings F-Radar and Signal Processing, 1992, 139(5): 343–350. doi: 10.1049/ip-f-2.1992.0048 [7] ZENG Tao, CHANG Shaoqiang, FAN Huayu, et al. Design and processing of a novel chaos-based stepped frequency synthesized wideband radar signal[J]. Sensors (Basel) , 2018, 18(4): 985. doi: 10.3390/s18040985 [8] ROHLING H and MOLLER C. Radar waveform for automotive radar systems and applications[C]. 2008 IEEE Radar Conference, Rome, Italy, 2008: 1–4. doi: 10.1109/RADAR.2008.4721121. [9] NGUYEN Q, PARK M, KIM Y, et al. 77 GHz waveform generator with multiple frequency shift keying modulation for multi-target detection automotive radar applications[J]. Electronics Letters, 2015, 51(8): 595–596. doi: 10.1049/el.2015.0092 [10] KRONAUGE M and ROHLING H. New chirp sequence radar waveform[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(4): 2870–2877. doi: 10.1109/TAES.2014.120813 [11] TAGHAVI I, SABAHI M F, and PARVARESH F. High resolution compressed sensing radar using difference set codes[J]. IEEE Transactions on Signal Processing, 2019, 67(1): 136–148. doi: 10.1109/TSP.2018.2878545 [12] HYUN E and LEE J H. Waveform design with dual ramp-sequence for high-resolution range-velocity FMCW radar[J]. Elektronika Ir Elektrotechnika, 2016, 22(4): 46. [13] KIM W, CHO H, KIM J, et al. YOLO-based simultaneous target detection and classification in automotive FMCW radar system[J]. Sensors, 2020, 20(10): 2897. doi: 10.3390/S20102897 [14] WANG Shuangling, HE Qian, and HE Zishu. LFM-based waveform design for cognitive MIMO radar with constrained bandwidth[J]. EURASIP Journal on Advances in Signal Processing, 2014, 2014(1): 89. doi: 10.1186/1687-6180-2540-89 [15] PATOLE S M, TORLAK M, WANG Dan, et al. Automotive radars: A review of signal processing techniques[J]. IEEE Signal Processing Magazine, 2017, 34(2): 22–35. doi: 10.1109/MSP.2016.2628914 [16] 郝天铎, 周青松, 孙从易, 等. 非准确先验知识下认知雷达低峰均比稳健波形设计[J]. 电子与信息学报, 2018, 40(3): 532–540. doi: 10.11999/JEIT170560HAO Tianduo, ZHOU Qingsong, SUN Congyi, et al. Low-PAR robust waveform design for cognitive radar with imprecise prior knowledge[J]. Journal of Electronics &Information Technology, 2018, 40(3): 532–540. doi: 10.11999/JEIT170560 [17] WANG Hongyan and PEI Bingnan. Robust waveform design for MIMO-STAP in the case of imperfect clutter prior knowledge[J]. Journal of Signal Processing, 2015, 31(11): 1418–1424. doi: 10.1007/s00034-015-0116-3 [18] PIOTROWSKY L, JAESCHKE T, KUEPPERS S, et al. Enabling high accuracy distance measurements with FMCW radar sensors[J]. IEEE Transactions on Microwave Theory and Techniques, 2019, 67(12): 5360–5371. doi: 10.1109/TMTT.2019.2930504 [19] WON Y S, SHIN D, JUNG S, et al. Method to improve degraded range resolution due to non-ideal factors in FMCW radar[J]. IEICE Electronics Express, 2019, 16(1): 20180924. doi: 10.1587/elex.15.20180924 [20] HAKOBYAN G and YANG Bin. High-performance automotive radar: A review of signal processing algorithms and modulation schemes[J]. IEEE Signal Processing Magazine, 2019, 36(5): 32–44. doi: 10.1109/MSP.2019.2911722 [21] IVANOV S I, KUPTSOV V D, and FEDOTOV A A. The signal processing algorithm of automotive FMCW radars with an extended range of speed estimation[J]. Journal of Physics: Conference Series, 2019, 1236: 012081. doi: 10.1088/1742-6596/1236/1/012081 [22] DATTA B N. Numerical Linear Algebra and Applications[M]. 2nd ed. Philadelphia: Society for Industrial and Applied Mathematics, 2010. [23] 李慧, 赵永波, 程增飞. 基于线性调频时宽的MIMO雷达正交波形设计[J]. 电子与信息学报, 2018, 40(5): 1151–1158. doi: 10.11999/JEIT170426LI Hui, ZHAO Yongbo, and CHENG Zengfei. MIMO radar orthogonal waveform set design based on chirp durations[J]. Journal of Electronics &Information Technology, 2018, 40(5): 1151–1158. doi: 10.11999/JEIT170426 -





 下载:
下载:



 下载:
下载:
