Design and Implementation of Memristor-based Chaotic Synchronization under a Single Input Controller
-
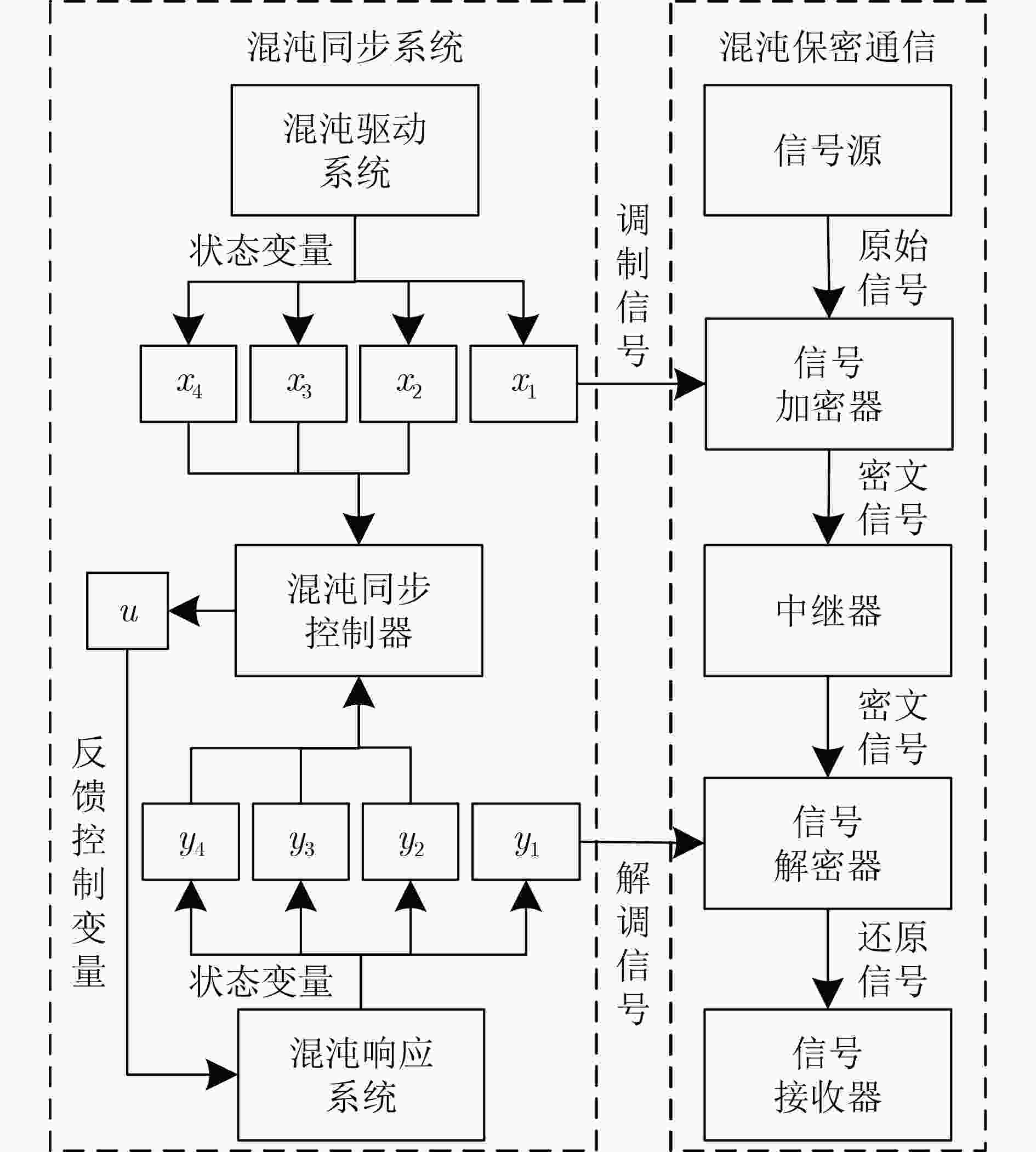
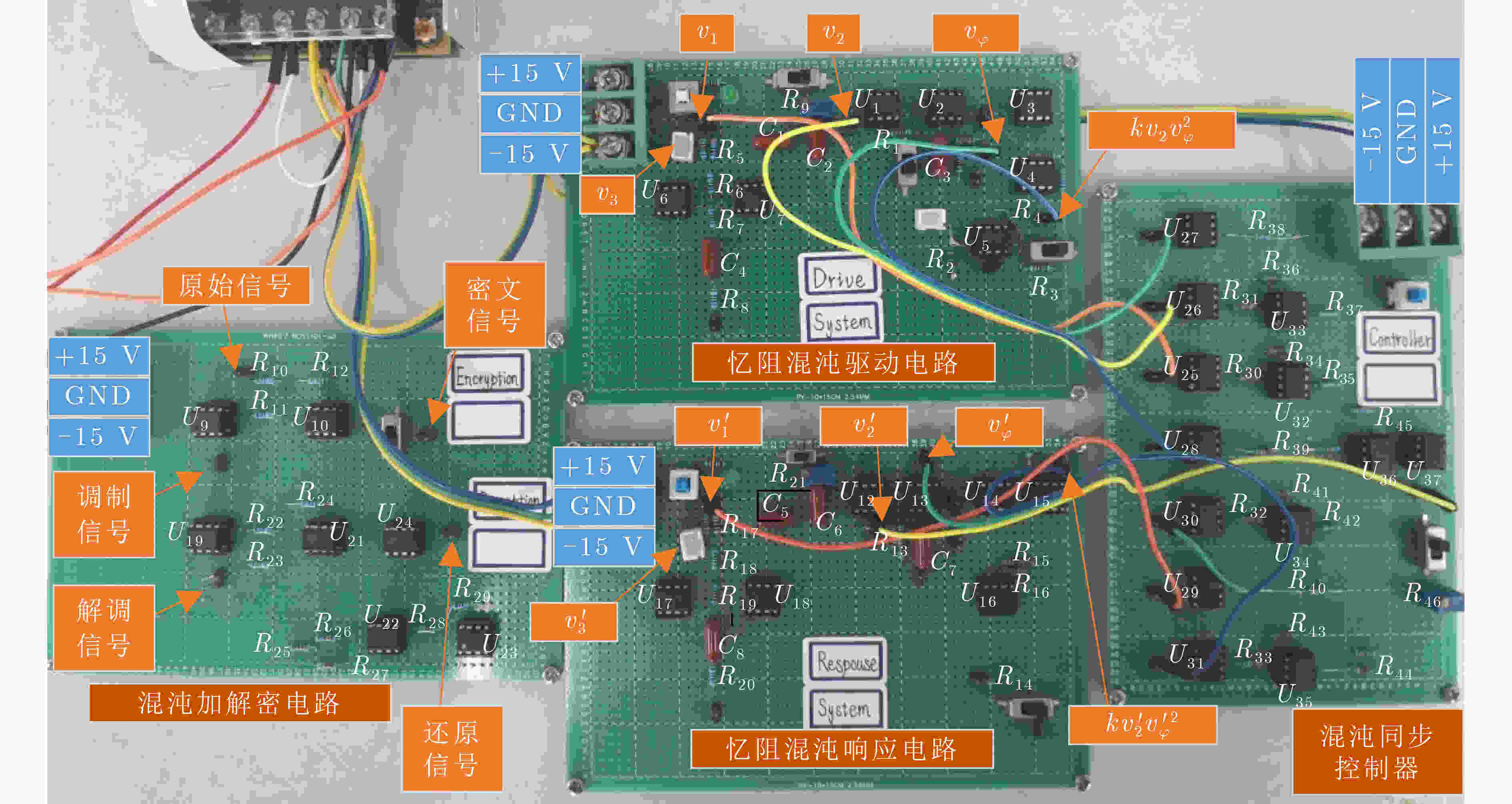
摘要: 该文提出一种在单输入控制器下基于忆阻器的混沌同步模拟电路设计及其实现方法,并将它应用于基于忆阻混沌同步的保密通信。首先,基于混沌同步理论,构建了混沌同步系统及保密通信模型,并设计实现了一种4阶压控忆阻混沌电路和混沌加密解密电路。其次,将所设计的忆阻混沌电路作为混沌驱动和响应电路,根据它们的误差系统设计了一种单输入混沌同步控制器,并将其实现于忆阻混沌同步电路当中。最后,完成了基于忆阻混沌同步的保密通信电路实验。实验结果表明,所设计忆阻混沌同步电路结构简单、操作方便、波形良好,在单输入控制器下电路能够快速同步并保持稳定,且在保密通信实验中信号还原度高、受损程度小、抗破译能力强,具有一定的理论意义与潜在的实用价值。Abstract: A memristor-based chaotic synchronization circuit is designed and implemented under a single-input controller, and it is applied to secure communication based on memristor chaotic synchronization. Firstly, based on the chaotic synchronization theory, a chaotic synchronization system and secure communication model are constructed, and a fourth-order memristor-based chaotic circuit is implemented, the chaotic en-/decryption circuit is also designed. Secondly, the proposed memristor-based chaotic circuit is considered as the chaotic drive and response circuits, and a single-input chaotic synchronization controller is designed according to their error system, and it is implemented in the memristor-based chaotic synchronization circuit. Finally, many experiments of chaotic synchronization and secure communication based on chaotic synchronization are performed, and experimental results show that the proposed memristor-based chaotic synchronization circuit has many advantages, such as simple structure, convenient operation and good waveform. Furthermore, secure communication based on chaotic synchronization has high signal recovery capability and good anti-decipher ability, so that it has certain theoretical significance and potential practical value.
-
Key words:
- Chaotic synchronous circuit /
- Memristor /
- Controller /
- Secure communication
-
表 1 系统参数
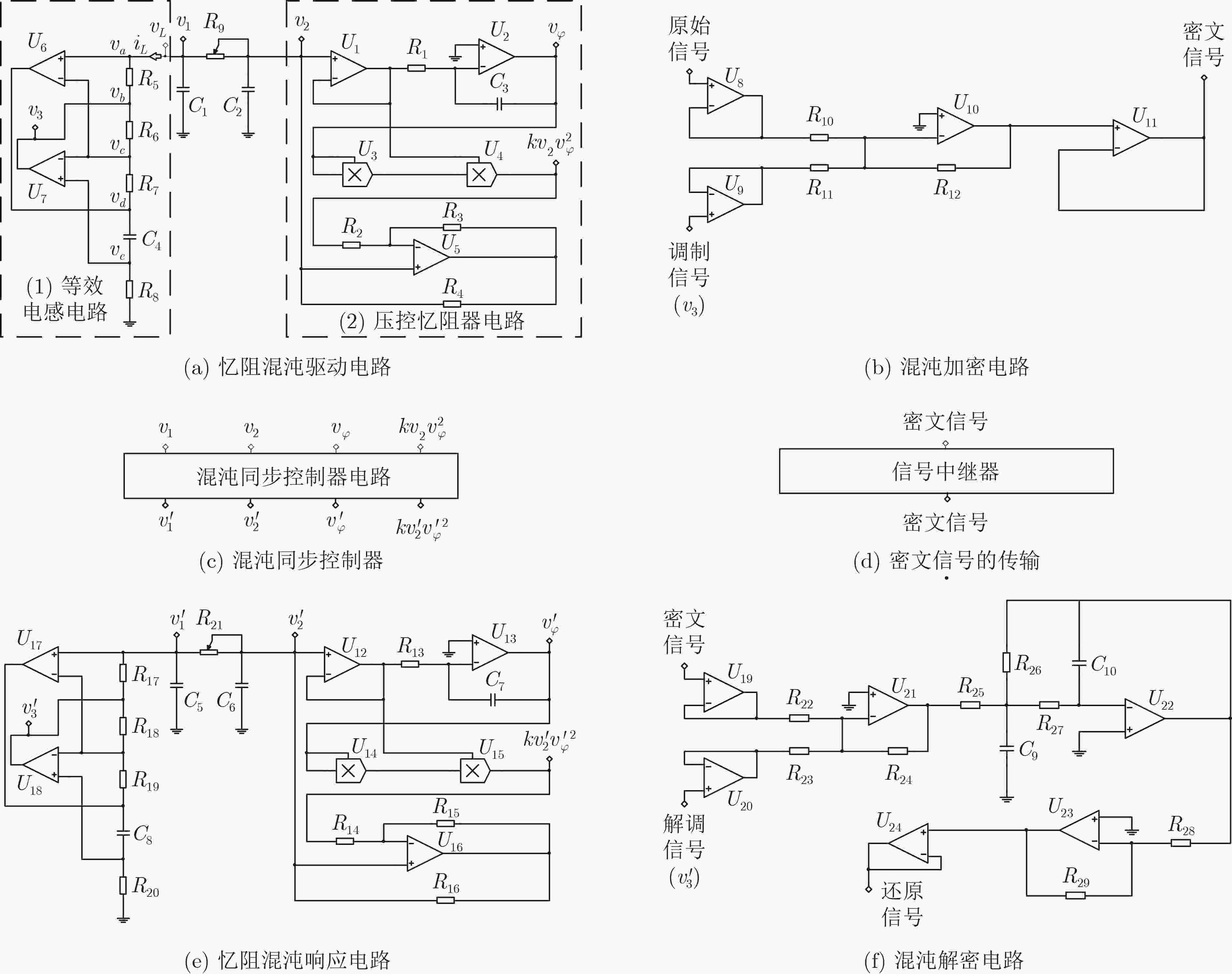
参数 $ \alpha $ $ \beta $ $ \chi $ $ \delta $ $ \varepsilon $ $ \gamma $ 表达式 $ \dfrac{1}{{{R_9}{C_1}}} $ $ \dfrac{1}{{{R_5}{C_1}}} $ $ \dfrac{{{R_6}}}{{{R_7}{R_8}{C_1}}} $ $ \dfrac{1}{{{R_9}{C_2}}} $ $ \dfrac{1}{{{C_2}}} $ $ \dfrac{1}{{{R_1}{C_3}}} $ 表 2 基于忆阻混沌同步的保密通信电路参数取值
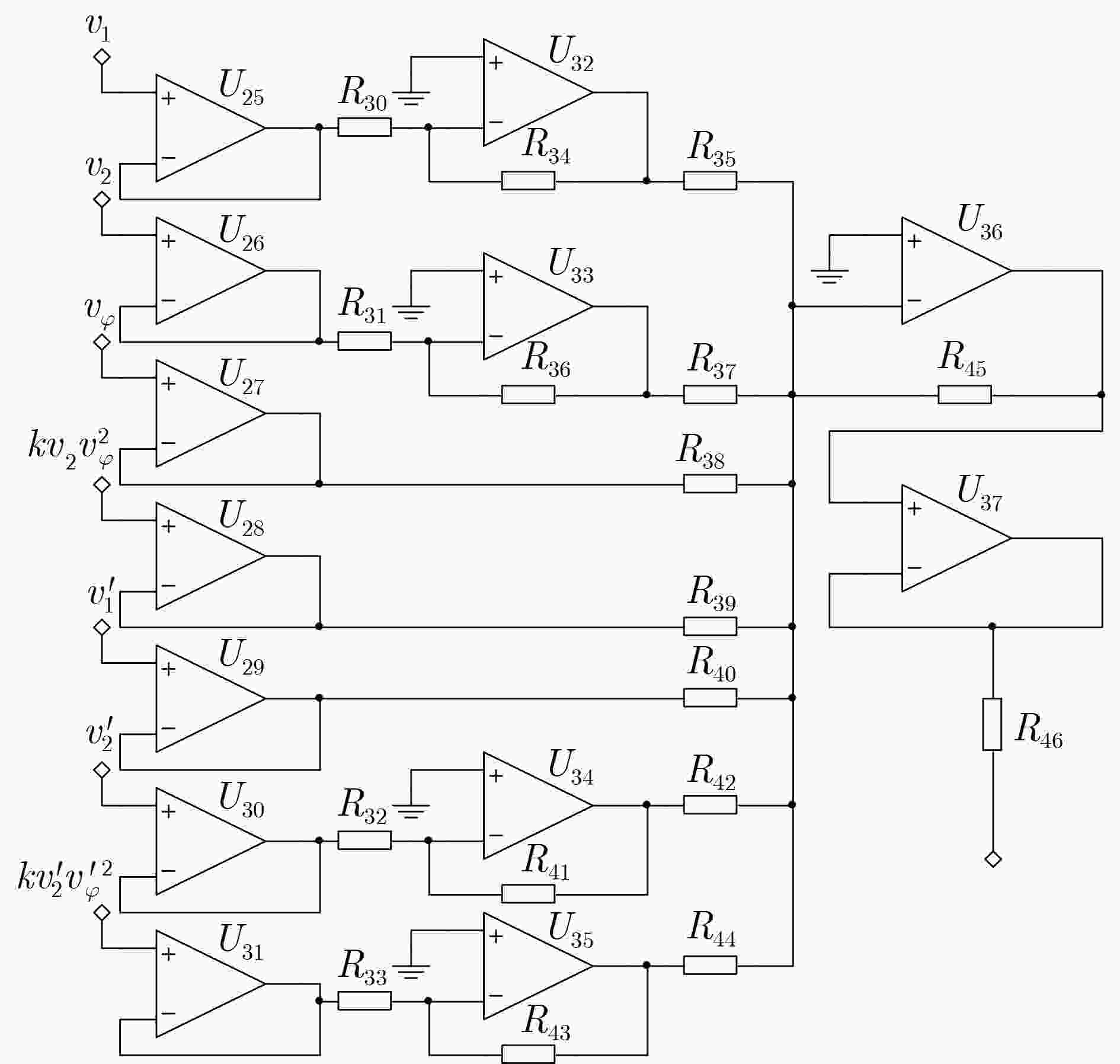
参数 参值 参数 参值 参数 参值 参数 参值 $ {R_1} $,$ {R_{13}} $ 8.2 kΩ $ {R_2} $,$ {R_{14}} $ 1.5 kΩ $ {R_3} $,$ {R_4} $,$ {R_{15}} $,$ {R_{16}} $ 2 kΩ $ {R_5} $,$ {R_{17}} $ 264 Ω $ {R_6} $,$ {R_7} $,$ {R_{18}} $,$ {R_{19}} $ 500 Ω $ {R_8} $,$ {R_{20}} $,$ {R_{28}} $,$ {R_{29}} $ 1 kΩ $ {R_9} $,$ {R_{21}} $,$ {R_{46}} $ 2.14 kΩ $ {R_{10}} $,$ {R_{24}} $ 39 kΩ $ {R_{11}} $,$ {R_{23}} $ 15 kΩ $ {R_{12}} $,$ {R_{22}} $ 11 kΩ $ {R_{25}} $,$ {R_{26}} $ 27 kΩ $ {R_{27}} $ 43 kΩ $ {R_{30}} $,$ {R_{31}} $,$ {R_{32}} $,$ {R_{33}} $ 10 kΩ $ {R_{34}} $,$ {R_{36}} $,$ {R_{41}} $,$ {R_{43}} $ 10 kΩ $ {R_{35}} $,$ {R_{37}} $,$ {R_{38}} $,$ {R_{40}} $ 18 kΩ $ {R_{39}} $,$ {R_{44}} $ 12.62 kΩ $ {R_{45}} $ 18 kΩ $ {C_1} $,$ {C_4} $,$ {C_5} $,$ {C_8} $ 68 nF $ {C_2} $,$ {C_6} $ 6.8 nF $ {C_3} $,$ {C_7} $ 47 nF $ {C_9} $ 10 nF $ {C_{10}} $ 2.2 nF 表 3 同步后各状态变量的误差信号统计
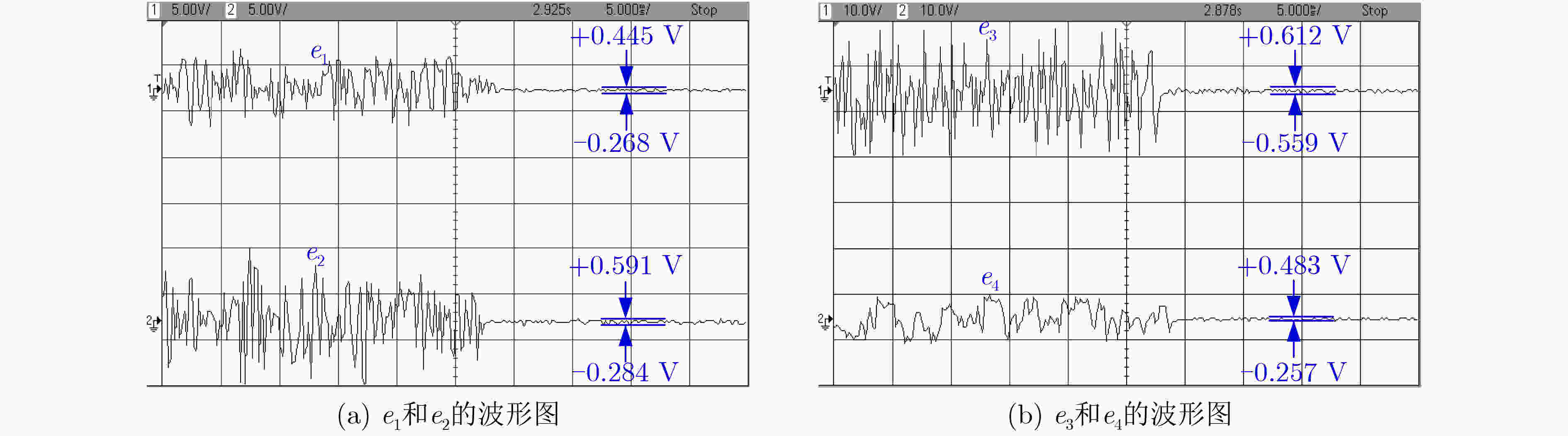
参数 最大值(V) 最小值(V) Matlab仿真 $ {e_1} $ 0.0003 –0.0002 $ {e_2} $ 0.0005 –0.0004 $ {e_3} $ 0.0012 –0.0008 $ {e_4} $ 0.0004 –0.0001 电路仿真 $ {e_1} $ 0.1070 –0.0610 $ {e_2} $ 0.0850 –0.0450 $ {e_3} $ 0.2410 –0.0970 $ {e_4} $ 0.0940 –0.0380 实际电路 $ {e_1} $ 0.4450 –0.2680 $ {e_2} $ 0.5910 –0.2840 $ {e_3} $ 0.6120 –0.5590 $ {e_4} $ 0.4830 –0.2570 -
[1] CHUA L. Memristor-the missing circuit element[J]. IEEE Transactions on Circuit Theory, 1971, 18(5): 507–519. doi: 10.1109/tct.1971.1083337 [2] STRUKOV D B, SNIDER G S, STEWART D R, et al. The missing memristor found[J]. Nature, 2008, 453(7191): 80–83. doi: 10.1038/nature06932 [3] MANNAN Z I, YANG Changju, and KIM H. Oscillation with 4-lobe Chua corsage memristor[J]. IEEE Circuits and Systems Magazine, 2018, 18(2): 14–27. doi: 10.1109/MCAS.2018.2821724 [4] BAO Han, JIANG Tao, CHU Kaibin, et al. Memristor-based canonical Chua’s circuit: Extreme multistability in voltage-current domain and its controllability in flux-charge domain[J]. Complexity, 2018, 2018: 5935637. doi: 10.1155/2018/5935637 [5] 林毅, 刘文波, 沈骞. 五阶压控忆阻蔡氏混沌电路的双稳定性[J]. 物理学报, 2018, 67(23): 230502. doi: 10.7498/aps.67.20181283LIN Yi, LIU Wenbo, and SHEN Qian. Bi-stability in a fifth-order voltage-controlled memristor-based Chua’s chaotic circuit[J]. Acta Physica Sinica, 2018, 67(23): 230502. doi: 10.7498/aps.67.20181283 [6] GUO Mei, YANG Wenyan, XUE Youbao, et al. Multistability in a physical memristor-based modified Chua’s circuit[J]. Chaos, 2019, 29(4): 043114. doi: 10.1063/1.5089293 [7] 吕晏旻, 闵富红. 基于现场可编程逻辑门阵列的磁控忆阻电路对称动力学行为分析[J]. 物理学报, 2019, 68(13): 130502. doi: 10.7498/aps.68.20190453LÜ Yanmin and MIN Fuhong. Dynamic analysis of symmetric behavior in flux-controlled memristor circuit based on field programmable gate array[J]. Acta Physica Sinica, 2019, 68(13): 130502. doi: 10.7498/aps.68.20190453 [8] HUANG Lilian, YAO Wenju, XIANG Jianhong, et al. Heterogeneous and homogenous multistabilities in a novel 4d memristor-based chaotic system with discrete bifurcation diagrams[J]. Complexity, 2020, 2020: 2408460. doi: 10.1155/2020/2408460 [9] MA Xujiong, MOU Jun, LIU Jian, et al. A novel simple chaotic circuit based on memristor–memcapacitor[J]. Nonlinear Dynamics, 2020, 100(3): 2859–2876. doi: 10.1007/s11071-020-05601-x [10] 王春华, 蔺海荣, 孙晶如, 等. 基于忆阻器的混沌、存储器及神经网络电路研究进展[J]. 电子与信息学报, 2020, 42(4): 795–810. doi: 10.11999/JEIT190821WANG Chunhua, LIN Hairong, SUN Jingru, et al. Research progress on chaos, memory and neural network circuits based on memristor[J]. Journal of Electronics &Information Technology, 2020, 42(4): 795–810. doi: 10.11999/JEIT190821 [11] PECORA L M and CARROLL T L. Synchronization of chaotic systems[J]. Chaos, 2015, 25(9): 097611. doi: 10.1063/1.4917383 [12] YE Xiaolin, WANG Xingyuan, GAO Suo, et al. A new chaotic circuit with multiple memristors and its application in image encryption[J]. Nonlinear Dynamics, 2020, 99(2): 1489–1506. doi: 10.1007/s11071-019-05370-2 [13] LUO Jing, QU Shaocheng, CHEN Yao, et al. Synchronization of memristor-based chaotic systems by a simplified control and its application to image en-/decryption using DNA encoding[J]. Chinese Journal of Physics, 2019, 62: 374–387. doi: 10.1016/j.cjph.2019.09.031 [14] SUN Junwei, YANG Qinfei, and WANG Yanfeng. Dynamical analysis of novel memristor chaotic system and DNA encryption application[J]. Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 2020, 44(1): 449–460. doi: 10.1007/s40998-019-00239-x [15] CHEN Baoju, YU Simin, CHEN Ping, et al. Design and virtex-7-based implementation of video chaotic secure communications[J]. International Journal of Bifurcation and Chaos, 2020, 30(5): 2050075. doi: 10.1142/S0218127420500753 [16] ZHAO Qing, WANG Chunhua, and ZHANG Xin. A universal emulator for memristor, memcapacitor, and meminductor and its chaotic circuit[J]. Chaos, 2019, 29(1): 013141. doi: 10.1063/1.5081076 [17] ZHU Minghao, WANG Chunhua, DENG Quanli, et al. Locally active memristor with three coexisting pinched hysteresis loops and its emulator circuit[J]. International Journal of Bifurcation and Chaos, 2020, 30(13): 2050184. doi: 10.1142/S0218127420501849 [18] WANG Chunhua, XIA Hu, and ZHOU Ling. A memristive hyperchaotic multiscroll jerk system with controllable scroll numbers[J]. International Journal of Bifurcation and Chaos, 2017, 27(6): 1750091. doi: 10.1142/S0218127417500912 [19] HAN Chunyan, SHEN Yiran, WU Zeyan, et al. A novel meminductor-based chaotic oscillating circuit and its DSP realisation for generating PN sequences[J]. Pramana, 2020, 94(1): 101. doi: 10.1007/s12043-020-01969-y [20] QUAN Boan, WANG Chunhua, SUN Jingru, et al. A novel adaptive active control projective synchronization of chaotic systems[J]. Journal of Computational and Nonlinear Dynamics, 2018, 13(5): 051001. doi: 10.1115/1.4039189 [21] RAJAGOPAL K, JAHANSHAHI H, VARAN M, et al. A hyperchaotic memristor oscillator with fuzzy based chaos control and LQR based chaos synchronization[J]. AEU-International Journal of Electronics and Communications, 2018, 94: 55–68. doi: 10.1016/j.aeue.2018.06.043 [22] YU Fei, QIAN Shuai, CHEN Xi, et al. A new 4D four-wing memristive hyperchaotic system: Dynamical analysis, electronic circuit design, shape synchronization and secure communication[J]. International Journal of Bifurcation and Chaos, 2020, 30(10): 2050147. doi: 10.1142/S0218127420501473 [23] KYPRIANIDIS I M, BOGIATZI A N, PAPADOPOULOU M, et al. Synchronizing chaotic attractors of Chua’s canonical circuit: The case of uncertainty in chaos synchronization[J]. International Journal of Bifurcation and Chaos, 2006, 16(7): 1961–1976. doi: 10.1142/S0218127406015829 [24] KOUNTCHOU M, LOUODOP P, BOWONG S, et al. Optimal synchronization of a memristive chaotic circuit[J]. International Journal of Bifurcation and Chaos, 2016, 26(6): 1650093. doi: 10.1142/S0218127416500930 [25] RAJAGOPAL K, KINGNI S T, KHALAF A J M, et al. Coexistence of attractors in a simple chaotic oscillator with fractional-order-memristor component: Analysis, FPGA implementation, chaos control and synchronization[J]. The European Physical Journal Special Topics, 2019, 228(10): 2035–2051. doi: 10.1140/epjst/e2019-900001-8 [26] HASHEMI S, POURMINA M A, MOBAYEN S, et al. Design of a secure communication system between base transmitter station and mobile equipment based on finite-time chaos synchronisation[J]. International Journal of Systems Science, 2020, 51(11): 1969–1986. doi: 10.1080/00207721.2020.1781290 -





 下载:
下载:




 下载:
下载:
