Energy Consumption Optimization Algorithm for Full-Duplex Relay-Assisted Mobile Edge Computing Systems
-
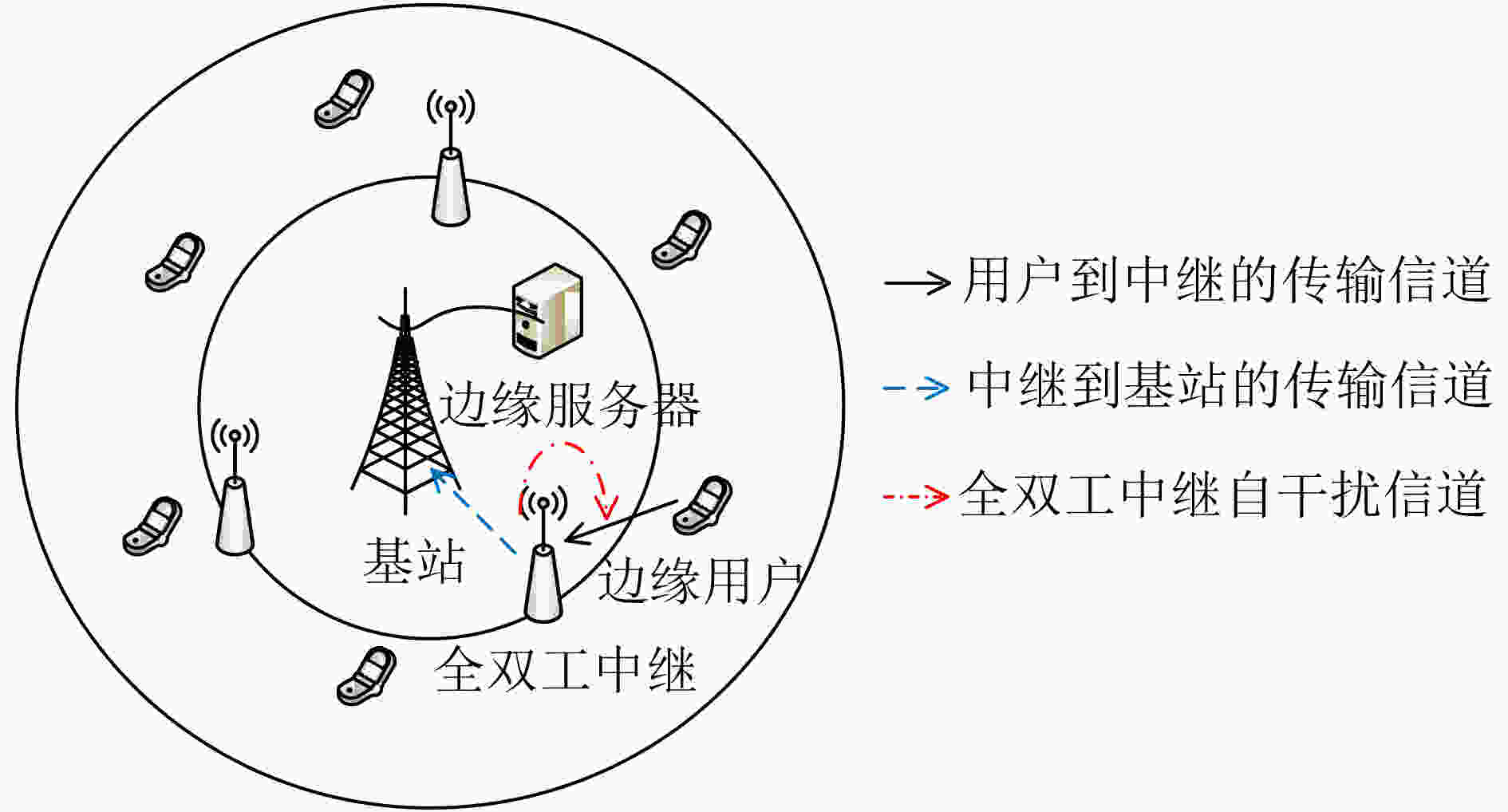
摘要: 为缓解终端设备处理大数据量、低时延业务的压力,该文提出一种基于全双工中继的移动边缘计算网络资源分配算法。首先,在满足计算任务时延约束、用户最大计算能力、用户和中继的最大发射功率约束条件下,考虑中继选择与子载波分配因子、用户任务卸载系数、用户与中继的传输功率的联合优化,建立了系统总能耗最小化问题。其次,利用交替迭代和变量代换的方法,将原非凸问题分解为两个凸优化子问题,并利用内点法和拉格朗日对偶原理分别进行求解。仿真结果表明,所提算法具有较低的能量消耗。Abstract: In order to alleviate the pressure of terminal devices to deal with the big-data and low-delay services, a resource allocation algorithm is studied for mobile edge computing networks with full-duplex relays. Firstly, the constraints of the maximum task latency, the maximum computing ability of users, and the maximum transmit power of users and relays are considered for achieving total energy consumption minimization by jointly optimizing the relay selection and subcarrier allocation factor, user task offloading coefficient, and the transmission power of users and relays. Secondly, based on the alternating iteration method and the variable-substitution approach, the originally non-convex problem is decomposed into two convex subproblems, which are solved by using the interior-point method and Lagrange dual theory, respectively. Simulation results show that the proposed algorithm has low energy consumption.
-
Key words:
- Full-duplex based relays /
- Mobile edge computing /
- Resource allocation
-
算法1 基于交替迭代的资源分配算法 1.初始化系统参数:$ p_n^{\max } $,$ P_m^{\max } $, $ T_n^{\max } $, $ F_n^{\max } $, $ \kappa $, $ B $, $K$,$ h_{n,m}^k $, $ {\sigma ^2} $, $ g_m^k $, $f_n^{\text{M}}$, ${S_n}$, ${C_n}$, $\varphi $, $\sigma _{{\text{SI}}}^2$;定义交替迭代算法收敛精度$\ell $;初始化交替迭
代次数$t$;定义外层最大迭代次数${T_{\max }}$;定义Dinkelbach迭代算法收敛精度$\zeta $以及相应最大迭代次数${L_{\max }}$;初始化梯度迭代次数$l$,初始化
$q = 0$;
2.给定$ \alpha _{n,m}^k(t) $和$ \bar p_{n,m}^k(t) $,利用内点法求解问题式(18),得到$ x_{n,m}^k(t + 1) $;
3.给定$ x_{n,m}^k(t + 1) $,给定q,求解问题式(20),得到当前最优值$ \bar p_{n,m}^k(l) $,$ \alpha _{n,m}^k(l) $;
4.当$ \left| {x_{n,m}^k(t + 1){S_n}\bar p_{n,m}^k(l) - q\bar R_{n,m}^k(l)} \right| \ge \zeta $,或者$l \le {L_{\max }}$;
5.令Flag=0,更新$l = l + 1$;
6.将$q$更新为$ q = {{x_{n,m}^k(t + 1){S_n}\bar p_{n,m}^k(l)} \mathord{\left/ {\vphantom {{x_{n,m}^k(t + 1){S_n}\bar p_{n,m}^k(l)} {\bar R_{n,m}^k(l)}}} \right. } {\bar R_{n,m}^k(l)}} $,结束并执行步骤3;
7.当$ \left| {x_{n,m}^k(t + 1){S_n}\bar p_{n,m}^k(l) - q\bar R_{n,m}^k(l)} \right| \le \zeta $,或者$l = {L_{\max }}$;
8.令Flag=1,更新并输出$ \alpha _{n,m}^{}(t + 1){\text{ = }}\alpha _{n,m}^l(l) $,$ \bar p_{n,m}^k(t + 1) = \bar p_{n,m}^k(l) $;
9.当$ \left| {\{ E_n^{\text{L}}(t + 1) + \alpha _{n,m}^k(t + 1)E_n^{{\text{UT}}}(t + 1)\} - \{ E_n^{\text{L}}(t) + \alpha _{n,m}^k(t)E_n^{{\text{UT}}}(t)\} } \right| \ge \ell $,或者$t \le {T_{\max }}$;
10.更新$t = t + 1$,执行步骤2;
11.结束并输出。表 1 仿真参数
参数 值 参数 值 $\phi $/(${\text{cycles} } \cdot {\text{bi} }{ {\text{t} }^{ {{ - 1} } } }$) 40 $\kappa $ ${10^{ - 24}}$ $F_n^{\max }$/cycles ${10^9}$ $ P_m^{\max } $/W 5 $ f_n^M $/cycles ${10^{10}}$ $ p_n^{\max } $/W 1 $K$ 5 $ \chi $ 3 ${\sigma ^2}$/mW ${10^{ - 6}}$ $ B $/Hz ${10^6}$ -
[1] LIU Yaqiong, PENG Mugen, SHOU Guochu, et al. Toward edge intelligence: Multiaccess edge computing for 5G and internet of things[J]. IEEE Internet of Things Journal, 2020, 7(8): 6722–6747. doi: 10.1109/JIOT.2020.3004500 [2] MAO Yuyi, YOU Changsheng, ZHANG Jun, et al. A survey on mobile edge computing: The communication perspective[J]. IEEE Communications Surveys & Tutorials, 2017, 19(4): 2322–2358. doi: 10.1109/COMST.2017.2745201 [3] 谢人超, 廉晓飞, 贾庆民, 等. 移动边缘计算卸载技术综述[J]. 通信学报, 2018, 39(11): 138–155. doi: 10.11959/j.issn.1000-436x.2018215XIE Renchao, LIAN Xiaofei, JIA Qingmin, et al. Survey on computation offloading in mobile edge computing[J]. Journal on Communications, 2018, 39(11): 138–155. doi: 10.11959/j.issn.1000-436x.2018215 [4] 李国权, 徐勇军, 陈前斌. 基于干扰效率多蜂窝异构无线网络最优基站选择及功率分配算法[J]. 电子与信息学报, 2020, 41(2): 957–964. doi: 10.11999/JEIT190419LI Guoquan, XU Yongjun, and CHEN Qianbin. Interference efficiency-based base station selection and power allocation algorithm for multi-cell heterogeneous wireless networks[J]. Journal of Electronics &Information Technology, 2020, 41(2): 957–964. doi: 10.11999/JEIT190419 [5] ZHANG Jing, XIA Weiwei, YAN Feng, et al. Joint computation offloading and resource allocation optimization in heterogeneous networks with mobile edge computing[J]. IEEE Access, 2018, 6: 19324–19337. doi: 10.1109/ACCESS.2018.2819690 [6] WANG Jingrong, LIU Kaiyang, and PAN Jianping. Online UAV-mounted edge server dispatching for mobile-to-mobile edge computing[J]. IEEE Internet of Things Journal, 2020, 7(2): 1375–1386. doi: 10.1109/JIOT.2019.2954798 [7] QIAN Liping, FENG Anqi, HUANG Yupin, et al. Optimal SIC ordering and computation resource allocation in MEC-aware NOMA NB-IoT networks[J]. IEEE Internet of Things Journal, 2019, 6(2): 2806–2816. doi: 10.1109/JIOT.2018.2875046 [8] SUN Haijian, ZHOU Fuhui, and HU R Q. Joint offloading and computation energy efficiency maximization in a mobile edge computing system[J]. IEEE Transactions on Vehicular Technology, 2019, 68(3): 3052–3056. doi: 10.1109/tvt.2019.2893094 [9] SONG Zhengyu, LIU Yuanwei, and SUN Xin. Joint radio and computational resource allocation for NOMA-based mobile edge computing in heterogeneous networks[J]. IEEE Communications Letters, 2018, 22(12): 2559–2562. doi: 10.1109/LCOMM.2018.2875984 [10] REN Jinke, YU Guanding, HE Yinghui, et al. Collaborative cloud and edge computing for latency minimization[J]. IEEE Transactions on Vehicular Technology, 2019, 68(5): 5031–5044. doi: 10.1109/TVT.2019.2904244 [11] CHEN Xihan, CAI Yunlong, SHI Qingjiang, et al. Efficient resource allocation for relay-assisted computation offloading in mobile-edge computing[J]. IEEE Internet of Things Journal, 2020, 7(3): 2452–2468. doi: 10.1109/JIOT.2019.2957728 [12] XIE Biyuan, ZHANG Qi, and QIN Jiayin. Joint optimization of cooperative communication and computation in two-way relay MEC systems[J]. IEEE Transactions on Vehicular Technology, 2020, 69(4): 4596–4600. doi: 10.1109/TVT.2020.2973292 [13] LAN Yanwen, WANG Xiaoxiang, WANG Dongyu, et al. Mobile-edge computation offloading and resource allocation in heterogeneous wireless networks[C]. Proceedings of 2019 IEEE Wireless Communications and Networking Conference, Marrakesh, Morocco, 2019: 1–6. doi: 10.1109/WCNC.2019.8885793. [14] ALAM S, MARK J W, and SHEN X S. Relay selection and resource allocation for multi-user cooperative OFDMA networks[J]. IEEE Transactions on Wireless Communications, 2013, 12(5): 2193–2205. doi: 10.1109/TWC.2013.032113.120652 [15] WEN Dingzhu, YU Guanding, LI Rongpeng, et al. Results on energy- and spectral-efficiency tradeoff in cellular networks with full-duplex enabled base stations[J]. IEEE Transactions on Wireless Communications, 2017, 16(3): 1494–1507. doi: 10.1109/TWC.2016.2647593 [16] CHEN Lei, YU F R, JI Hong, et al. Distributed virtual resource allocation in small-cell networks with full-duplex self-backhauls and virtualization[J]. IEEE Transactions on Vehicular Technology, 2016, 65(7): 5410–5423. doi: 10.1109/TVT.2015.2469149 [17] DINKELBACH W. On nonlinear fractional programming[J]. Management Science, 1967, 13(7): 492–498. doi: 10.1287/mnsc.13.7.492 [18] BOYD S and VANDENBERGHE L. Convex Optimization[M]. Cambridge: Cambridge University Press, 2004. [19] HUANG Kaizhi and ZHANG Bo. Robust secure transmission for wireless information and power transfer in heterogeneous networks[J]. IET Communications, 2019, 13(4): 411–422. doi: 10.1049/iet-com.2018.5529 [20] CROUZEIX J P and FERLAND J A. Algorithms for generalized fractional programming[J]. Mathematical Programming, 1991, 52(1/3): 191–207. doi: 10.1007/BF01582887 -





 下载:
下载:


 下载:
下载:
