Modeling and Simulation of HF Aeronautical Mobile Channel Based on Watterson Model
-
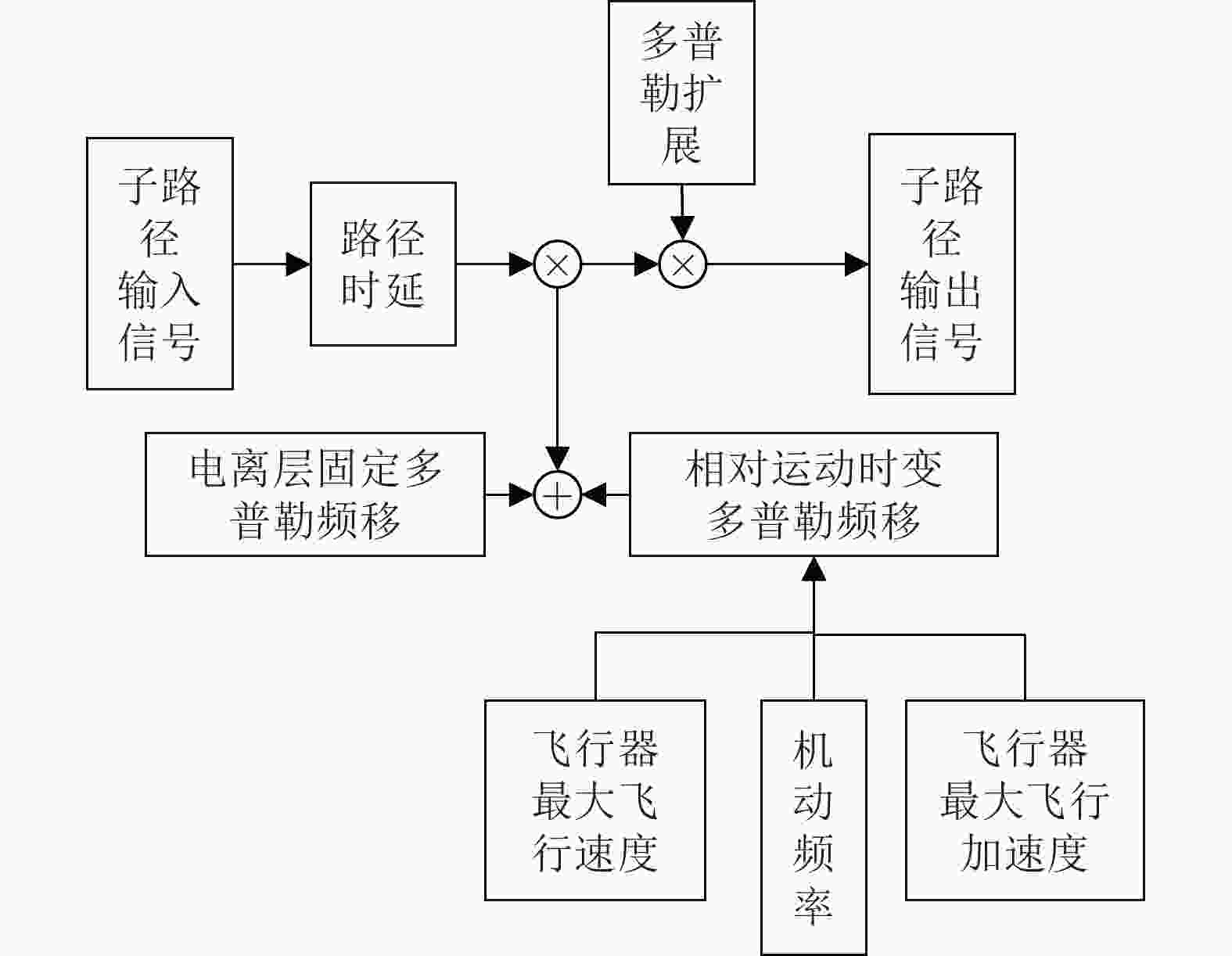
摘要: 信道建模与仿真是短波航空通信系统性能分析评估的基础,该文通过分析研究飞行器最大移动速度、加速度、机动频率、运动轨迹等机动状态参数对短波航空移动信道时变多普勒频移的影响,提出一种基于Watterson模型的短波航空移动信道模型。该模型能够充分描述由收发两端相对运动引入的信道多普勒频移与扩展,适用于短波超视距航空移动通信信道。仿真结果表明,该模型能够实现对不同种类不同机动状态飞行器短波移动通信信道的差异化仿真,还能在已知航线航迹时,实现对特定场景下的定制化信道仿真。
-
关键词:
- 短波通信 /
- 航空移动信道 /
- Watterson模型 /
- 信道仿真
Abstract: Channel modeling and simulation is the basis of performance analysis and evaluation of High frequency (HF) aviation communication system. A HF aviation mobile channel model based on Watterson model is proposed by analyzing the influence of maneuvering state parameters such as maximum moving speed, acceleration, maneuvering frequency and trajectory on the time-varying Doppler frequency shift. The model can fully describe the Doppler frequency shift and spread caused by the relative movement of the transmitter and receiver, and is suitable for HF over-the-horizon aeronautical mobile communication channel. The simulation results show that the model can realize the differential simulation of HF mobile communication channels for different types of aircraft with different maneuvering states, and can realize the customized channel simulation in specific scenarios when the route path is known.-
Key words:
- HF communication /
- Aeronautical channel /
- Watterson model /
- Channel simulation
-
表 1 3种典型场景下参数参考值
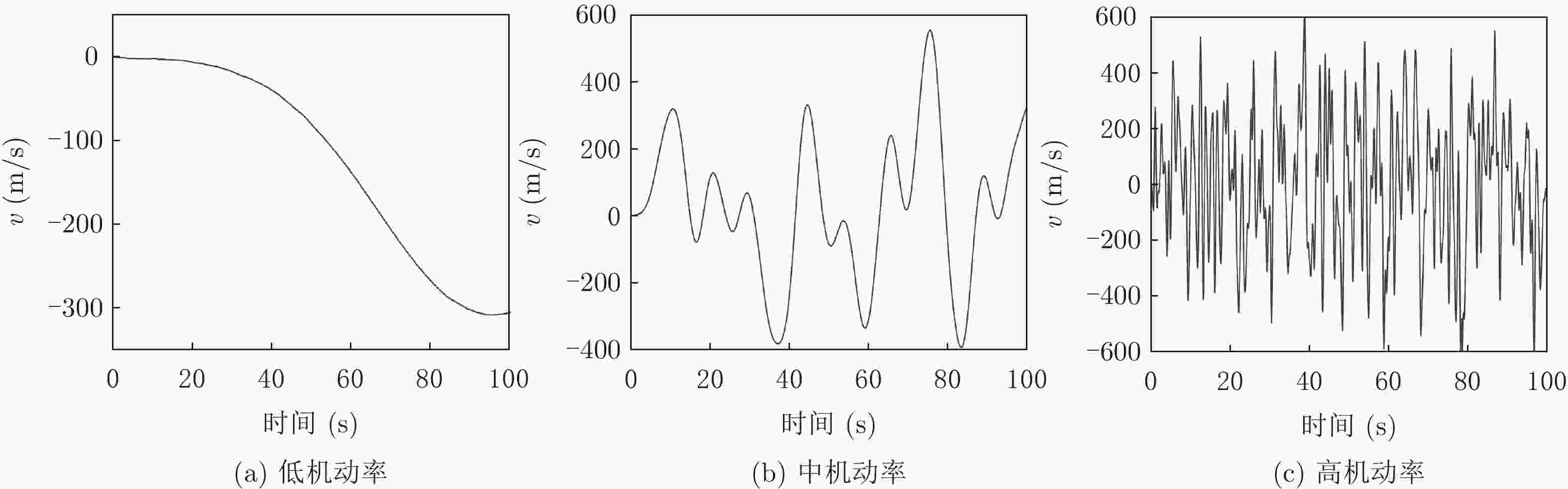
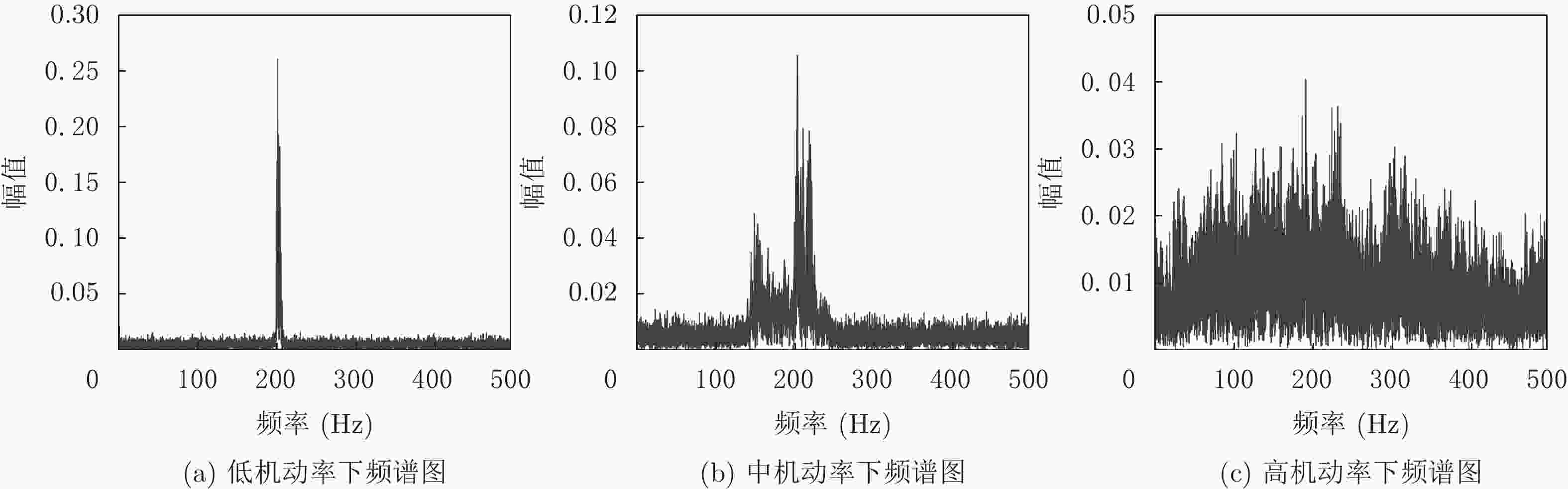
机动频率等级 典型应用场景 机动频率参考值(Hz) 飞行状态持续时间(s) 低 民用航空 0.01 ≥200 中 私人飞机等 0.1 10~20 高 无人载具等 1 ≤1 表 2 飞行器的飞行航线轨迹确定时运动参数
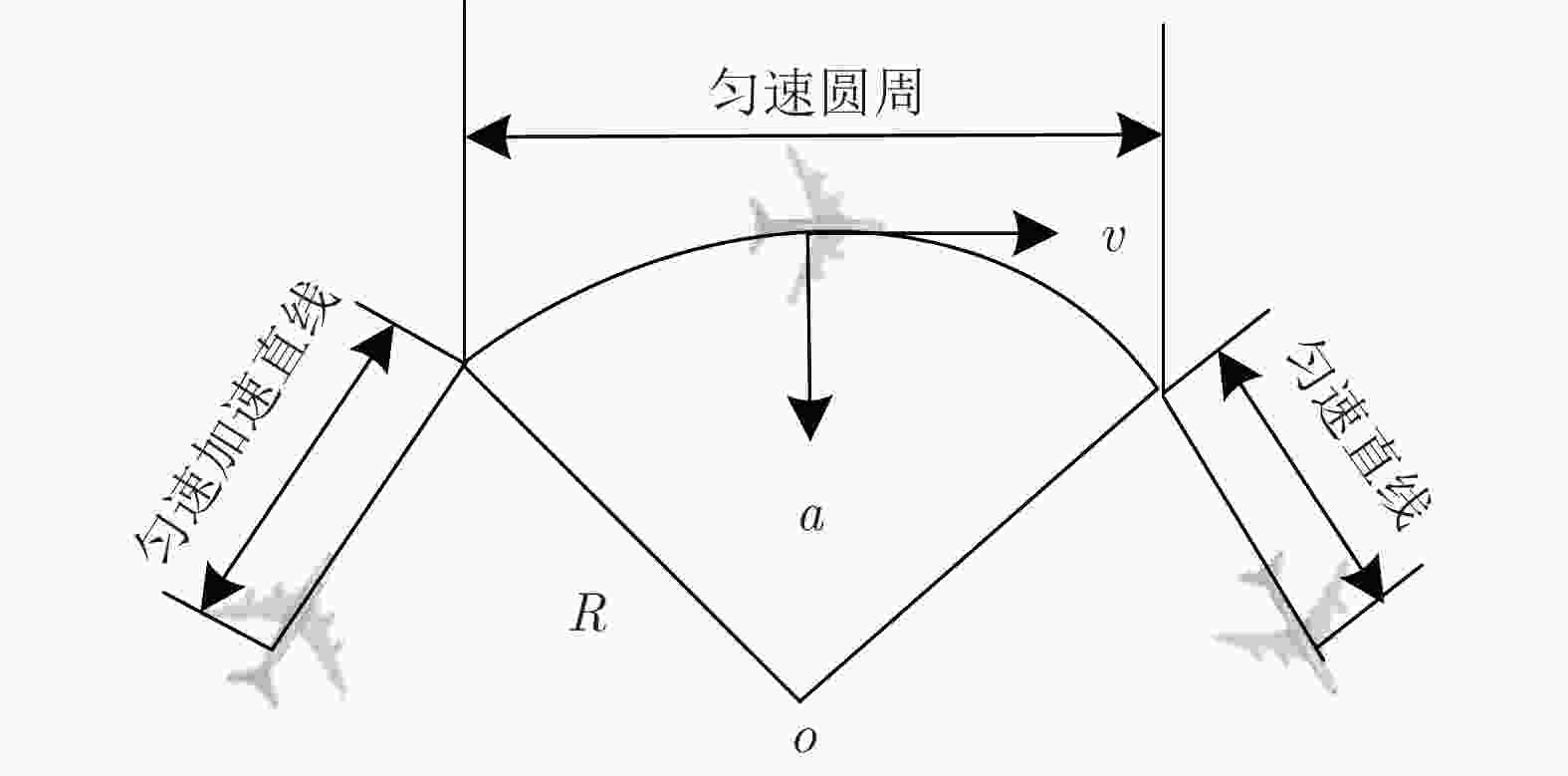
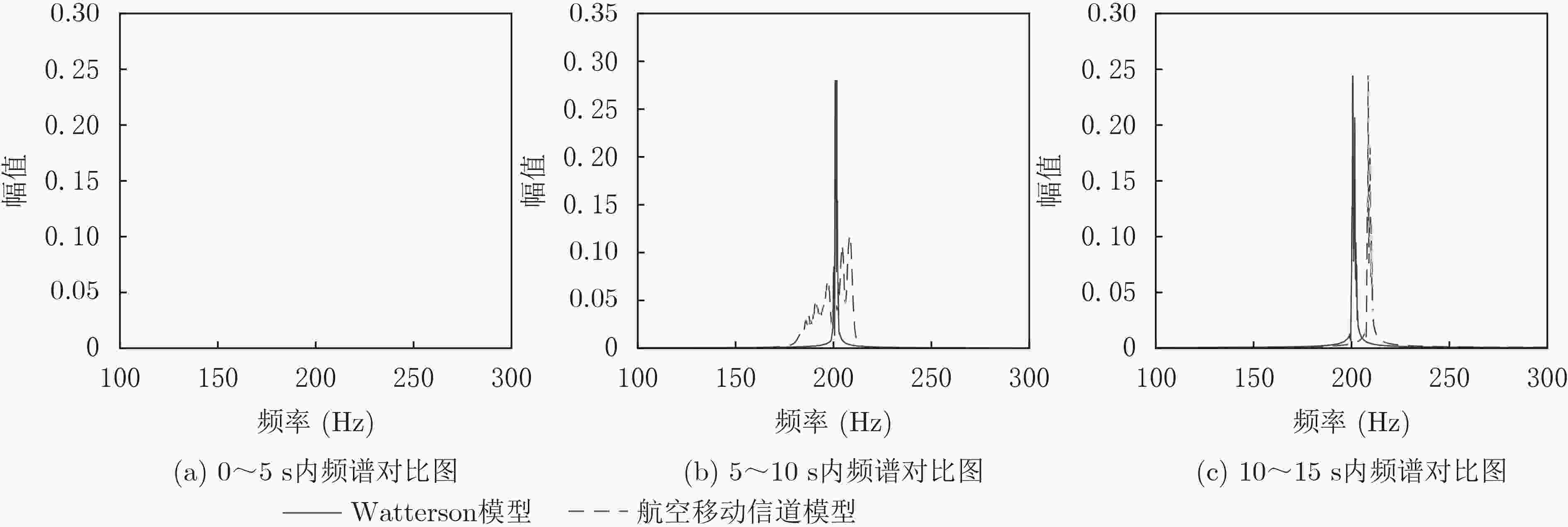
时间(s) 运动方式 初速度(m/s) 加速度(m/s2) 0~5 匀加速直线 0 50 5~10 匀速圆周(R=1000 m) 250 大小V2/R 方向时变 10~15 匀速直线 250 0 -
[1] 李国军, 徐小飞, 叶昌荣, 等. 面向远海岛礁环境监测的天波超视距传输技术[J]. 物联网学报, 2018, 2(3): 61–70. doi: 10.11959/j.issn.2096-3750.2018.00065LI Guojun, XU Xiaofei, YE Changrong, et al. A transmission technology of environmental monitoring for ocean based on over-the-horizon skywave[J]. Chinese Journal on Internet of Things, 2018, 2(3): 61–70. doi: 10.11959/j.issn.2096-3750.2018.00065 [2] LI Wen, RUAN Lang, XU Yifan, et al. Exploring channel diversity in HF communication systems: A matching-potential game approach[J]. China Communications, 2018, 15(9): 60–72. doi: 10.1109/CC.2018.8456452 [3] 吴永宏, 王程林, 任渊博, 等. 基于电离层色散的短波信道多径特性分析[J]. 电子与信息学报, 2020, 42(8): 2006–2012. doi: 10.11999/JEIT190384WU Yonghong, WANG Chenglin, REN Yuanbo, et al. High frequency channel multipath analysis based on ionosphere dispersion[J]. Journal of Electronics &Information Technology, 2020, 42(8): 2006–2012. doi: 10.11999/JEIT190384 [4] WATTERSON C C, JUROSHEK J R, and BENSEMA W D. Experimental confirmation of an HF channel model[J]. IEEE Transactions on Communication Technology, 1970, 18(6): 792–803. doi: 10.1109/TCOM.1970.1090438 [5] METELEV S A. Modification of the Watterson model of the ionospheric HF radio communication channel for adaptive spaced reception[J]. Radiophysics and Quantum Electronics, 2012, 55(4): 241–252. doi: 10.1007/s11141-012-9363-3 [6] VOGLER L E and HOFFMEYER J A. A model for wideband HF propagation channels[J]. Radio Science, 1993, 28(6): 1131–1142. doi: 10.1029/93RS01607 [7] YAN Zhaowen, ZHANG Lanlan, RAHMAN T, et al. Prediction of the HF ionospheric channel stability based on the modified ITS model[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(6): 3321–3333. doi: 10.1109/TAP.2013.2249571 [8] HAAS E. Aeronautical channel modeling[J]. IEEE Transactions on Vehicular Technology, 2002, 51(2): 254–264. doi: 10.1109/25.994803 [9] MATOLAK D W and SUN Ruoyu. Air-ground channel characterization for unmanned aircraft systems-Part I: Methods, measurements, and models for over-water settings[J]. IEEE Transactions on Vehicular Technology, 2017, 66(1): 26–44. doi: 10.1109/TVT.2016.2530306 [10] YAN Chaoxing, FU Lingang, ZHANG Jiankang, et al. A comprehensive survey on UAV communication channel modeling[J]. IEEE Access, 2019, 7: 107769–107792. doi: 10.1109/ACCESS.2019.2933173 [11] 王峥. 短波移动信道的仿真模型分析[J]. 南京邮电大学学报, 2005, 25(5): 31–34. doi: 10.3969/j.issn.1673-5439.2005.05.007WANG Zheng. Analysis on the simulation model of the HF mobile channel[J]. Journal of Nanjing University of Posts and Telecommunications, 2005, 25(5): 31–34. doi: 10.3969/j.issn.1673-5439.2005.05.007 [12] 孔豫京, 黄焱, 薛志刚, 等. 无人机短波频谱监测信道的改进ITS模型[J]. 信息工程大学学报, 2015, 16(6): 731–737. doi: 10.3969/j.issn.1671-0673.2015.06.017KONG Yujing, HUANG Yan, XUE Zhigang, et al. Improved ITS model of unmanned aircraft HF spectrum monitoring channel[J]. Journal of Information Engineering University, 2015, 16(6): 731–737. doi: 10.3969/j.issn.1671-0673.2015.06.017 [13] 仲伟志, 郭庆. 基于高动态运动模型的多普勒频移仿真[J]. 计算机工程, 2010, 36(20): 22–24. doi: 10.3969/j.issn.1000-3428.2010.20.008ZHONG Weizhi and GUO Qing. Doppler frequency shift simulation based on high dynamic motion model[J]. Computer Engineering, 2010, 36(20): 22–24. doi: 10.3969/j.issn.1000-3428.2010.20.008 [14] DATTA D, MITRA P, and DUTTA H S. FPGA implementation of high performance digital down converter for software defined radio[J]. Microsystem Technologies, To be published. doi: 10.1007/s00542-019-04579-w. [15] 钱广华, 李颖, 骆荣剑. 机动目标跟踪中一种机动频率和方差自适应滤波算法[J]. 雷达学报, 2013, 2(2): 257–264. doi: 10.3724/SP.J.1300.2013.13003QIAN Guanghua, LI Ying, and LUO Rongjian. One maneuvering frequency and the variance adaptive filtering algorithm for maneuvering target tracking[J]. Journal of Radars, 2013, 2(2): 257–264. doi: 10.3724/SP.J.1300.2013.13003 [16] ITU. ITU-R F. 1487 FRENCH-2000 Testing of HF modems with bandwidths of up to about 12 kHz using ionospheric channel simulators[S]. Geneva, Switzerland: International Telecommunications Union, 2000. -





 下载:
下载:


 下载:
下载:
