基于记忆多项式的时间交织模数转换器自适应非线性失配校正方法

刘素娟; 张仲侯

doi:10.11999/JEIT200885

基于记忆多项式的时间交织模数转换器自适应非线性失配校正方法

doi: 10.11999/JEIT200885

刘素娟^,,
张仲侯

北京工业大学微电子学院北京 100124

基金项目: 国家自然科学基金(62074010)，北京市教委科技项目(KM201810005022)

详细信息

作者简介:
刘素娟：女，1978年生，副教授，研究方向为模数混合集成电路设计

张仲侯：男，1995年生，硕士生，研究方向为模数混合集成电路设计

通讯作者:
刘素娟　liusujuan@bjut.edu.cn

中图分类号: TN911.72
计量
- 文章访问数: 602
- HTML全文浏览量: 389
- PDF下载量: 55
- 被引次数: 0
出版历程
- 收稿日期: 2020-10-16
- 修回日期: 2021-06-07
- 网络出版日期: 2021-07-15
- 刊出日期: 2021-12-21

Adaptive Nonlinear Mismatch Calibration Technique for TIADC Based on Memory Polynomial Model

Sujuan LIU^,,
Zhonghou ZHANG

College of Microelectronics, Beijing University of Technology, Beijing 100124, China

Funds: The National Natural Science Foundation of China (62074010), The Scientific Research Project of Beijing Educational Committee (KM201810005022)

摘要

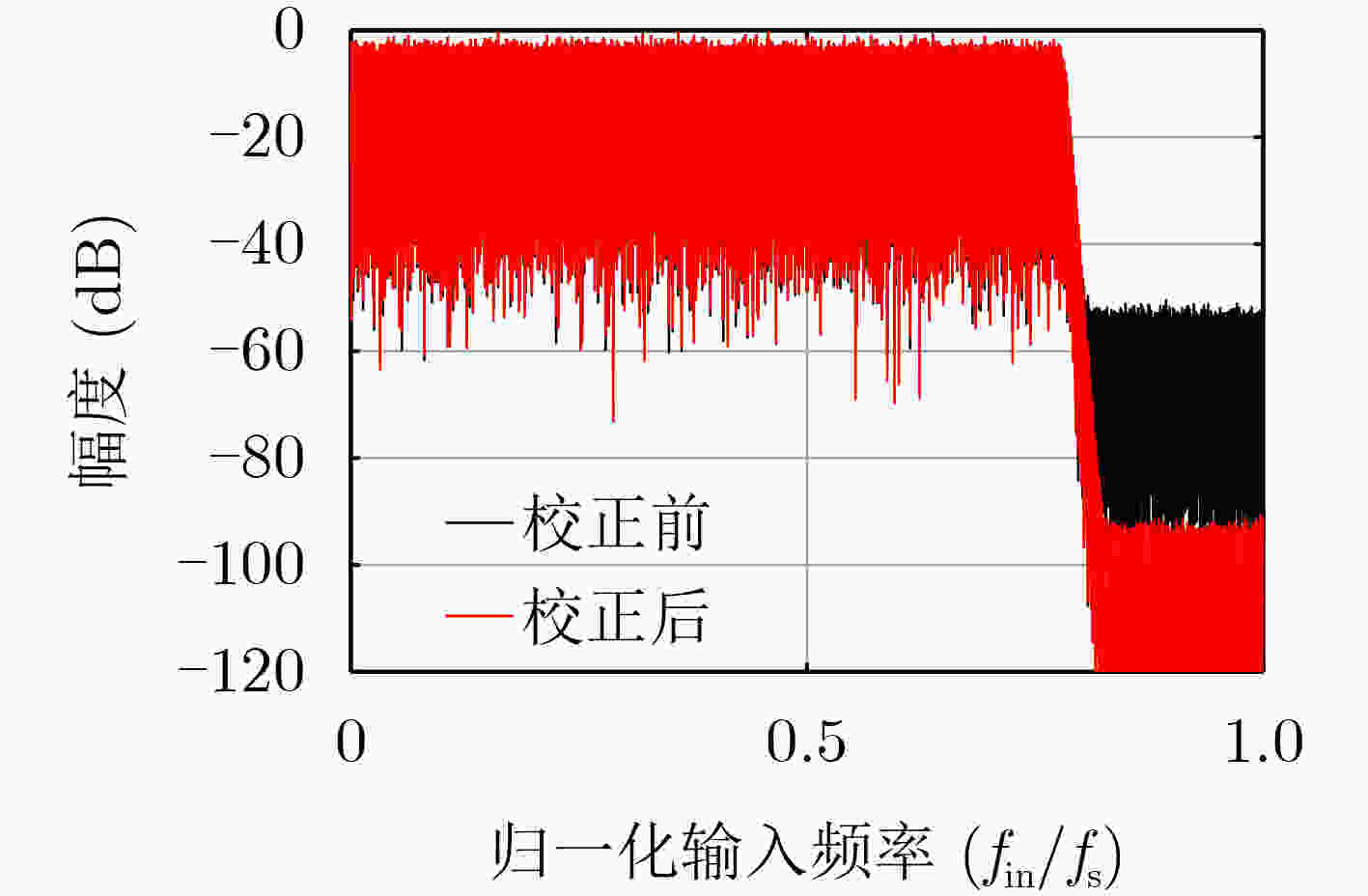
摘要: 为了提高时间交织模数转换器(TIADC)的有效分辨率，需要对其通道之间的线性/非线性失配误差进行估计和补偿。该文针对M通道TIADC的带有记忆效应的非线性失配误差提出了一种自适应盲校正算法。通过子通道重构结构(SCR)重构非线性误差信号，并通过滤波降采样最小均方(FDLMS)算法估计非线性失配误差系数。实验仿真结果表明，该方法可以有效校正带有记忆效应的非线性失配误差，并且可以大大降低实现难度和硬件资源消耗。
- 时间交织模数转换器 /
- 非线性失配误差 /
- 子通道重构结构 /
- 自适应盲校正
Abstract: To improve the effective resolution of the Time-Interleaved Analog-to-Digital Converter (TIADC), it is necessary to estimate and compensate the linear/non-linear mismatch error between its channels. An adaptive blind correction algorithm is proposed for the non-linear mismatch error of M-channel TIADC with memory effect. The nonlinear error signal is reconstructed through the Sub-Channel Reconstruction (SCR) structure, and the nonlinear mismatch error coefficient is estimated through the Filtered-Down-sampled Least Mean Square (FDLMS) algorithm. Experimental simulation results show that this method can effectively correct the non-linear mismatch error with memory effect, and can greatly reduce the difficulty of implementation and the consumption of hardware resources.
- Time-Interleaved Analog-to-Digital Converter (TIADC) /
- Nonlinear mismatch error /
- Sub-Channel Reconstruction (SCR) /
- Adaptive blind calibration

HTML全文

图 1 TIADC结构示意图

下载: 全尺寸图片幻灯片

图 2 带有记忆效应的非线性失配误差的子ADC的离散模型

下载: 全尺寸图片幻灯片

图 3 带有记忆效应的非线性失配误差的TIADC的离散模型

下载: 全尺寸图片幻灯片

图 4 M通道TIADC带有记忆效应的非线性误差校正原理结构图

下载: 全尺寸图片幻灯片

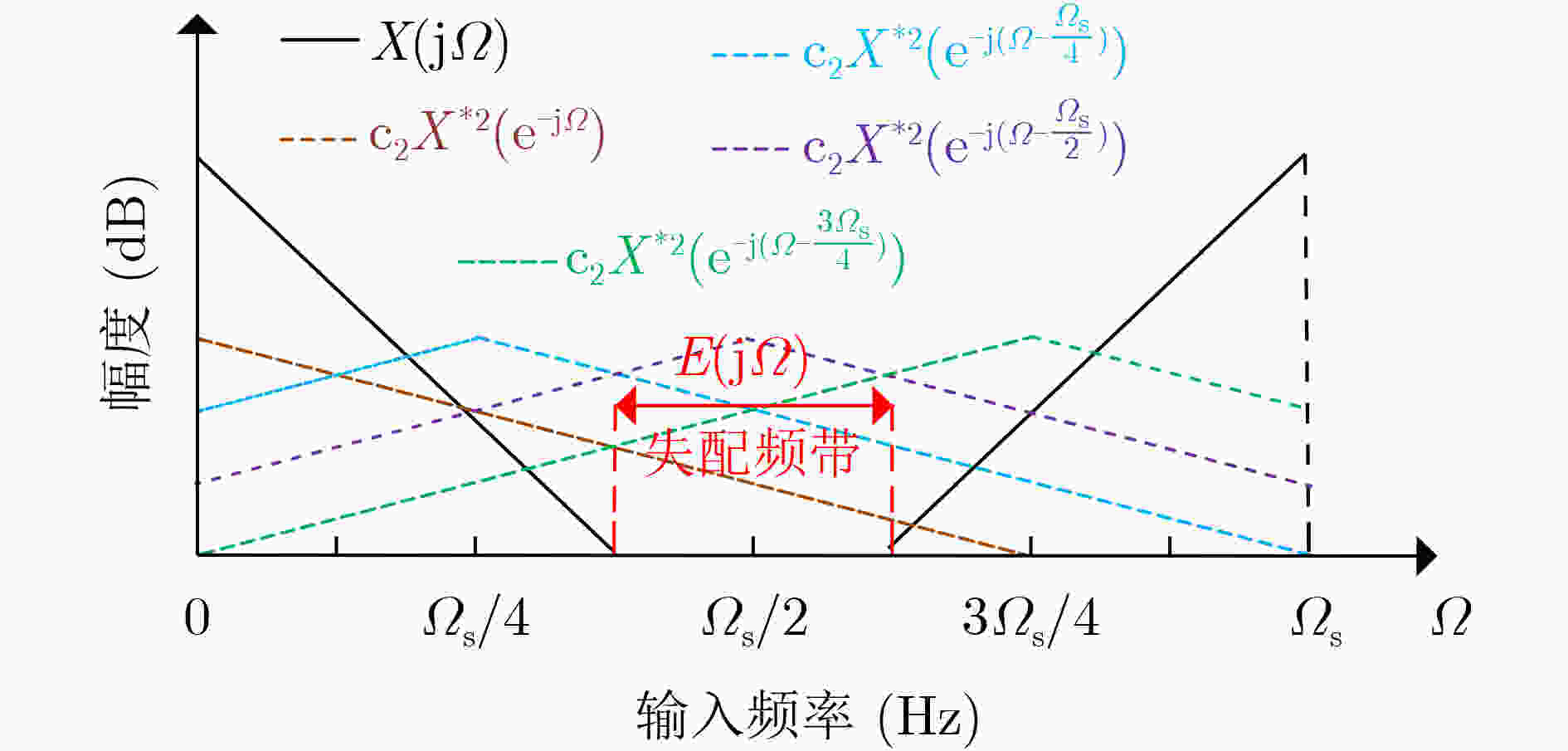
图 5 含有2阶非线性误差的四通道TIADC输入无关频带示意图^[7]

下载: 全尺寸图片幻灯片

图 6 基于FDLMS算法的M通道自适应盲校正算法结构示意图

下载: 全尺寸图片幻灯片

图 7 多频点输入信号校正效果示意图

下载: 全尺寸图片幻灯片

图 8 多频点输入信号情况下误差收敛曲线

下载: 全尺寸图片幻灯片

图 9 低通白噪声输入信号校正效果示意图

下载: 全尺寸图片幻灯片

图 10 低通白噪声输入信号情况下误差收敛曲线

下载: 全尺寸图片幻灯片

图 11 计算复杂度对比

下载: 全尺寸图片幻灯片

表 1 计算复杂度的对比

	本文	文献[16]	文献[17]
误差类型	带有记忆效应	静态	静态
通道数M	M=1, 2, ···	M=1, 2, ···	M=1, 2, 4, 8, ···
乘法器/每次采样	2(P–1)Q+N_f/2+1	(2M+1)(P–1)+N_f/2+1	(M+1)(P–1)+N_f/2+1
调制器/每次采样	0	(2M+1)(P–1)	(M+1)(P–1)
M：TIADC通道数；P：非线性误差最高阶；Q：记忆长度；N_f：高通FIR滤波器阶数

下载: 导出CSV

参考文献(21)

[1]	邓红辉, 闫辉, 肖瑞, 等. 一种全数字前馈式时间交织模数转换器时间误差后台校准算法[J]. 电子与信息学报, 2020, 42(2): 410–417. doi: 10.11999/JEIT190052 DENG Honghui, YAN Hui, XIAO Rui, et al. Fully digital feedforward background calibration of time skew for sub-sampling time-interleaved analog-to-digital converter[J]. Journal of Electronics &Information Technology, 2020, 42(2): 410–417. doi: 10.11999/JEIT190052
[2]	徐祥俊, 邹月娴. 基于频域稀疏性的时间交替模数转换器时间相位失配盲测量算法[J]. 电子与信息学报, 2012, 34(9): 2241–2246. doi: 10.3724/SP.J.1146.2012.00029 XU Xiangjun and ZOU Yuexian. A blind timing skews estimation algorithm of time-interleaved analog-to-digital converters based on spectra sparsity[J]. Journal of Electronics &Information Technology, 2012, 34(9): 2241–2246. doi: 10.3724/SP.J.1146.2012.00029
[3]	LIU Sujuan, LYU Ning, CUI Jiashuai, et al. Improved blind timing skew estimation based on spectrum sparsity and ApFFT in time-interleaved ADC[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(1): 76–83. doi: 10.1109/TIM.2018.2834080
[4]	BLACK W C and HODGES D A. Time interleaved converter arrays[J]. IEEE Journal of Solid-State Circuits, 1980, 15(6): 1022–1029. doi: 10.1109/JSSC.1980.1051512
[5]	VOGEL C. The impact of combined channel mismatch effects in time-interleaved ADCs[J]. IEEE Transactions on Instrumentation and Measurement, 2005, 54(1): 415–427. doi: 10.1109/TIM.2004.834046
[6]	JAMAL S M, FU Daihong, SINGH M P, et al. Calibration of sample-time error in a two-channel time-interleaved analog-to-digital converter[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2004, 51(1): 130–139. doi: 10.1109/TCSI.2003.821302
[7]	LIU Sujuan, LÜ Ning, MA Haixiao, et al. Adaptive semiblind background calibration of timing mismatches in a two-channel time-interleaved analog-to-digital converter[J]. Analog Integrated Circuits and Signal Processing, 2017, 90(1): 1–7. doi: 10.1007/s10470-016-0839-5
[8]	LIU Sujuan, MA Haixiao, LÜ Ning, et al. Adaptive blind timing mismatch calibration with low power consumption in M-channel time-interleaved ADC[J]. Circuits, Systems, and Signal Processing, 2018, 37(11): 4861–4879. doi: 10.1007/s00034-018-0788-6
[9]	HUANG S and LEVY B C. Blind calibration of timing offsets for four-channel time-interleaved ADCs[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2007, 54(4): 863–876. doi: 10.1109/TCSI.2006.888770
[10]	SEO M, RODWELL M J W, and MADHOW U. Comprehensive digital correction of mismatch errors for a 400-msamples/s 80-dB SFDR time-interleaved analog-to-digital converter[J]. IEEE Transactions on Microwave Theory and Techniques, 2005, 53(3): 1072–1082. doi: 10.1109/TMTT.2005.843487
[11]	SIMOES J B, LANDECK J, and CORREIA C M B A. Nonlinearity of a data-acquisition system with interleaving/multiplexing[J]. IEEE Transactions on Instrumentation and Measurement, 1997, 46(6): 1274–1279. doi: 10.1109/19.668271
[12]	VOGEL C and KUBIN G. Analysis and compensation of nonlinearity mismatches in time-interleaved ADC arrays[C]. 2004 IEEE International Symposium on Circuits and Systems, Vancouver, Canada, 2004.
[13]	VOGEL C, PAMMER V, and KUBIN G. A novel channel randomization method for time-interleaved ADCs[C]. 2005 IEEE Instrumentation and Measurement Technology Conference Proceedings, Ottawa, Canada, 2005: 150–155.
[14]	WEI Wentao, YE Peng, YANG Kuojun, et al. Compensation of dynamic nonlinear mismatches in time-interleaved analog-to-digital converter[J]. IEICE Electronics Express, 2019, 16(7): 1–6. doi: 10.1587/elex.16.20190020
[15]	WEI Wentao, YE Peng, SONG Jinpeng, et al. A behavioral dynamic nonlinear model for time-interleaved ADC based on volterra series[J]. IEEE Access, 2019, 7: 41860–41873. doi: 10.1109/ACCESS.2019.2905365
[16]	WANG Yinan, JOHANSSON H, XU Hui, et al. Bandwidth-efficient calibration method for nonlinear errors in M-channel time-interleaved ADCs[J]. Analog Integrated Circuits and Signal Processing, 2016, 86(2): 275–288. doi: 10.1007/s10470-015-0677-x
[17]	LIU Husheng, WANG Yinan, LI Nan, et al. A calibration method for nonlinear mismatches in M-channel time-interleaved analog-to-digital converters based on hadamard sequences[J]. Applied Sciences, 2016, 6(11): 362. doi: 10.3390/app6110362
[18]	LIU Xiangyu, XU Hui, JOHANSSON H, et al. Correlation-based calibration for nonlinearity mismatches in dual-channel TIADCs[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2020, 67(3): 585–589. doi: 10.1109/TCSII.2019.2916430
[19]	WANG Yinan, JOHANSSON H, XU Hui, et al. Joint blind calibration for mixed mismatches in two-channel time-interleaved ADCs[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2015, 62(6): 1508–1517. doi: 10.1109/TCSI.2015.2418835
[20]	GOODMAN J, MILLER B, HERMAN M, et al. Polyphase nonlinear equalization of time-interleaved analog-to-digital converters[J]. IEEE Journal of Selected Topics in Signal Processing, 2009, 3(3): 362–373. doi: 10.1109/JSTSP.2009.2020243
[21]	OPPENHEIM A V, SCHAFER R W, and BUCK J R. Discrete-Time Signal Processing[M]. 2nd ed. Upper Saddle River: Prentice Hall, 1999: 345–387.