Kernel Extreme Learning Machine Based on Alternating Direction Multiplier Method of Binary Splitting Operator
-
摘要: 凸优化形式的核极限学习机(KELM)具有较高的分类准确率,但用迭代法训练凸优化核极限学习机要较传统核极限学习机的解线性方程法花费更长时间。针对此问题,该文提出一种2元裂解算子交替方向乘子法(BSADMM-KELM)来提高凸优化核极限学习机的训练速度。首先引入2元裂解算子,将求核极限学习机最优解的过程分裂为两个中间算子的优化过程,再通过中间算子的迭代计算而得到原问题的最优解。在22个UCI数据集上所提算法的训练时间较有效集法平均快29倍,较内点法平均快4倍,分类精度亦优于传统的核极限学习机;在大规模数据集上该文算法的训练时间优于传统核极限学习机。Abstract: The Kernel Extreme Learning Machine (KELM) with convex optimization form has higher classification accuracy, but it takes longer time to train kelm with iterative method than solving linear equation method of traditional kelm. To solve this problem, an Alternating Direction Multiplier Method(ADMM) of Binary Splitting (BSADMM-KELM) is proposed to improve the training speed of convex optimization kernel extreme learning machine. Firstly, the process of finding the optimal solution of the kernel extreme learning machine is split into two intermediate operators by introducing a binary splitting operator, and then the optimal solution of the original problem is obtained through the iterative calculation of the intermediate operators. On 22 UCI datasets, the training time of the proposed algorithm is 29 times faster than that of the effective set method and 4 times faster than that of the interior point method. The classification accuracy of the proposed algorithm is also better than that of the traditional kernel extreme learning machine. On large-scale datasets, the training time of the proposed algorithm is better than that of the traditional kernel extreme learning machine.
-
表 1 解QP问题的2元裂解算子ADMM算法流程
输入:${{\boldsymbol{v}}^0},{{\boldsymbol{z}}^0},{{\boldsymbol{y}}^0}$,参数$\rho > 0,\sigma > 0,a \in (0,2)$,半正定矩阵${\boldsymbol{P}}$,矩阵${\boldsymbol{A}}$,单位矩阵${\boldsymbol{I}}$,向量${\boldsymbol{q}}$。 输出:最优解$v$。 步骤1 通过迭代寻找最优解: 1.1 解矩阵形式 $\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{P}} + \sigma {\boldsymbol{I}}}&{{{\boldsymbol{A}}^{\rm{T}}}} \\ {\boldsymbol{A}}&{ - {\rho ^{ - 1}}{\boldsymbol{I}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\tilde {\boldsymbol{v}}}^{k + 1}}} \\ {{{\boldsymbol{u}}^{k + 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\sigma {{\boldsymbol{v}}^k} - {\boldsymbol{q}}} \\ {{{\boldsymbol{z}}^k} - {\rho ^{ - 1}}{{\boldsymbol{y}}^k}} \end{array}} \right]$得到${\tilde {\boldsymbol{v}}^{k + 1}},{{\boldsymbol{u}}^{k + 1}}$的值; 1.2 $\tilde {\boldsymbol{z}} = {{\boldsymbol{z}}^k} + {\rho ^{ - 1}}({{\boldsymbol{u}}^{k + 1}} - {{\boldsymbol{y}}^k})$ 1.3 ${{\boldsymbol{v}}^{k + 1}} = a{\tilde {\boldsymbol{v}}^{k + 1}} + (1 - a){{\boldsymbol{v}}^k}$ 1.4 ${{\boldsymbol{z}}^{k + 1}} = {\prod _C}(a{\tilde {\boldsymbol{z}}^{k + 1}} + (1 - a){{\boldsymbol{z}}^k} + {\rho ^{ - 1}}{{\boldsymbol{y}}^k})$ 1.5 ${{\boldsymbol{y}}^{k + 1}} = {{\boldsymbol{y}}^k} + \rho (a{\tilde {\boldsymbol{z}}^{k + 1}} + (1 - a){{\boldsymbol{z}}^k} - {{\boldsymbol{z}}^{k + 1}})$ 步骤2 在约束条件内如果满足终止条件则输出${\boldsymbol{v}}$,否则转步骤1进行下一次迭代。 表 2 BSADMM-KELM的训练算法
输入:训练数据集X,测试数据集Y,约束条件$C$,核参数$\delta $,矩阵${\boldsymbol{A}}$,单位矩阵${\boldsymbol{I}}$,向量${\boldsymbol{q}}$。 输出:训练集和测试集分类准确率。 步骤1 载入训练样本和测试样本; 步骤2 对数据集X,Y进行预处理; 步骤3 根据模型式(5)计算半正定矩阵${\boldsymbol{P}}$; 步骤4 传入${\boldsymbol{P}},C,{\boldsymbol{A}},{\boldsymbol{I}},{\boldsymbol{q}}$调用表1算法,返回$N$个${v_i}$的最优值组成的${\boldsymbol{v}} = [{v_1},{v_2}, \cdots ,{v_N}]$; 步骤5 根据式(3)上面的性质求出所有的支持向量${{\boldsymbol{x}}_s}$; 步骤6 对于训练集X和测试集Y所有样本,根据式(3)计算其对应的分类类别; 步骤7 将每个样本得到的分类类别其真实值对比,所有样本对比完后输出分类准确率。 表 3 实验所用UCI数据集列表
数据集 样本数量 属性数目 数据集 样本数量 属性数目 Banknote 1372 4 Debrecen 1151 20 Fertility 100 10 Creditcard 30000 24 Hill 606 101 Occupancy 20560 7 Monks1 432 7 HTRU2 17898 9 Monks2 432 7 Heart 270 13 SPECTF 267 44 Australian 690 14 Pdspeech 1040 26 Liver 345 7 Epileptic 11500 179 Ionosphere 351 34 Mushroom 8124 22 Pima 768 9 Spambase 4601 57 Cancer 683 10 Adult 48842 14 Sonar 258 60 表 4 4种KELM算法训练时间和计算精度比较(自测)
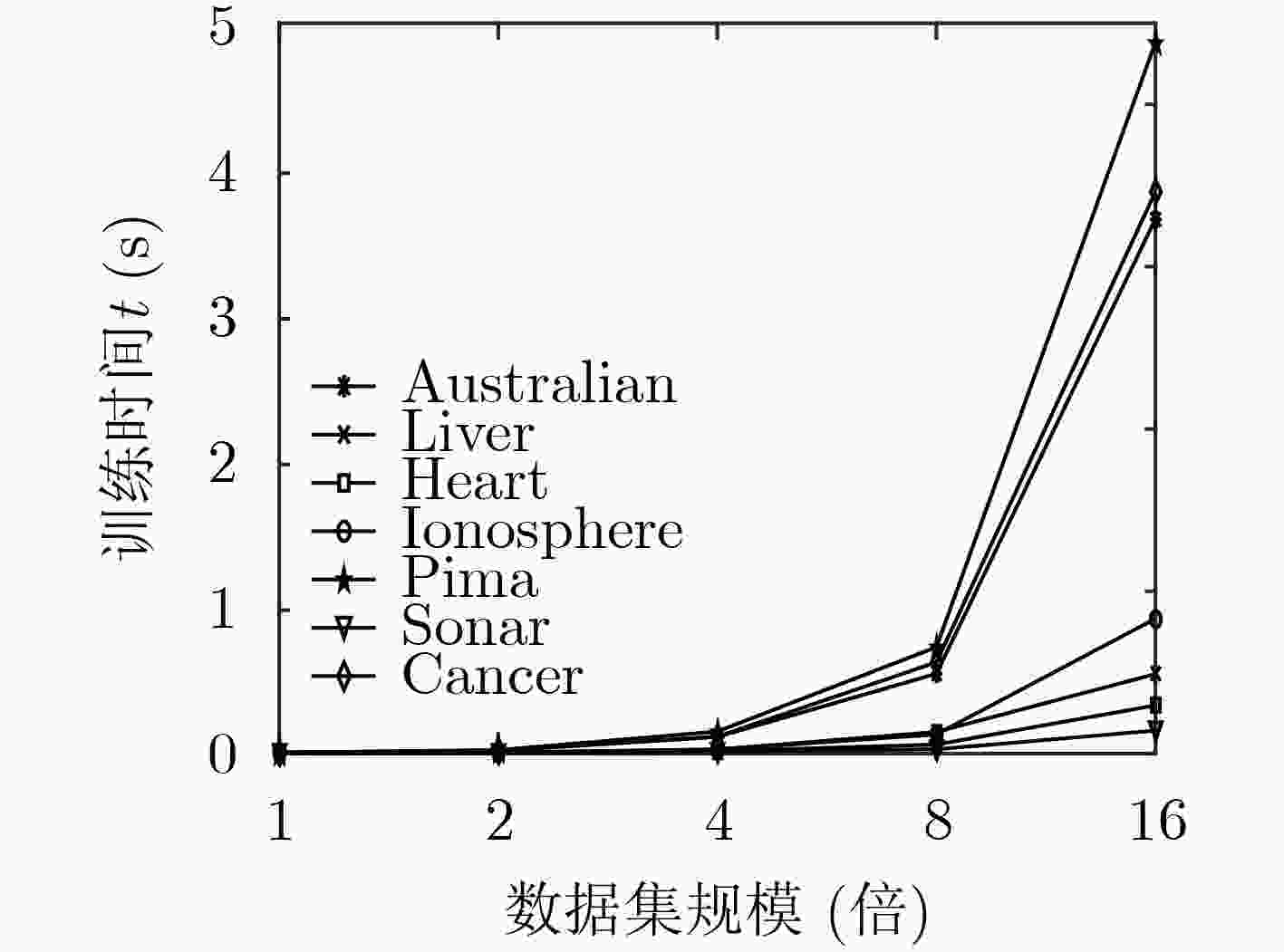
数据集 KELM MINQ-KELM MOSEK-KELM BSADMM-KELM 精度(%) 求解时间(s) 精度(%) 求解时间(s) 精度(%) 求解时间(s) 精度(%) 求解时间(s) Banknote 100.00 0.0673 100.00 1.5989 100.00 0.3014 100.00 0.0521 Fertility 86.00 0.0029 92.15 0.0999 91.25 0.0090 91.25 0.0018 Heart 82.96 0.0032 86.11 0.1318 88.43 0.0074 90.74 0.0007 Hill 58.09 0.0128 62.47 5.4970 60.41 0.1390 62.06 0.1950 Monks1 65.74 0.0070 97.36 0.1214 96.29 0.0361 98.31 0.0048 Monks2 68.98 0.0074 98.88 0.0765 99.63 0.0163 99.87 0.0021 SPECTF 85.71 0.0034 92.06 0.3839 93.93 0.0512 95.93 0.0107 Pdspeech 92.89 0.0878 89.40 2.7579 88.08 0.3429 94.55 0.0696 Epileptic 94.24 6.7190 95.90 86.0792 95.90 8.9292 96.78 8.4618 Mushroom 95.55 4.8600 95.31 23.4706 99.31 8.4933 98.40 5.5572 Spambase 88.04 0.6364 90.46 4.7311 92.02 1.6849 92.77 0.5321 Adult 81.74 89.2852 84.08 851.8944 84.19 134.0564 85.10 69.5138 Debrecen 62.61 0.0328 69.06 0.9339 69.92 0.0475 71.30 0.0324 Creditcard 77.00 80.2243 72.33 752.0268 80.46 97.3124 79.08 53.0256 Occupancy 98.05 25.8158 98.94 78.6522 98.95 30.4110 99.02 22.7719 HTRU2 96.37 14.2591 96.93 78.5169 97.88 10.4880 97.92 11.2290 Australian 88.22 0.0144 83.88 0.3019 84.63 0.3108 90.72 0.0198 Liver 63.77 0.0061 60.87 0.1657 66.30 0.0115 76.95 0.0059 Ionosphere 87.14 0.0042 84.64 0.0486 88.57 0.0095 96.43 0.0036 Pima 74.68 0.0145 75.41 0.4374 75.90 0.0177 79.12 0.0111 Cancer 95.79 0.0143 96.34 0.1310 94.87 0.0196 96.58 0.0170 Sonar 83.33 0.0026 75.90 0.0293 77.71 0.0066 95.58 0.0018 表 5
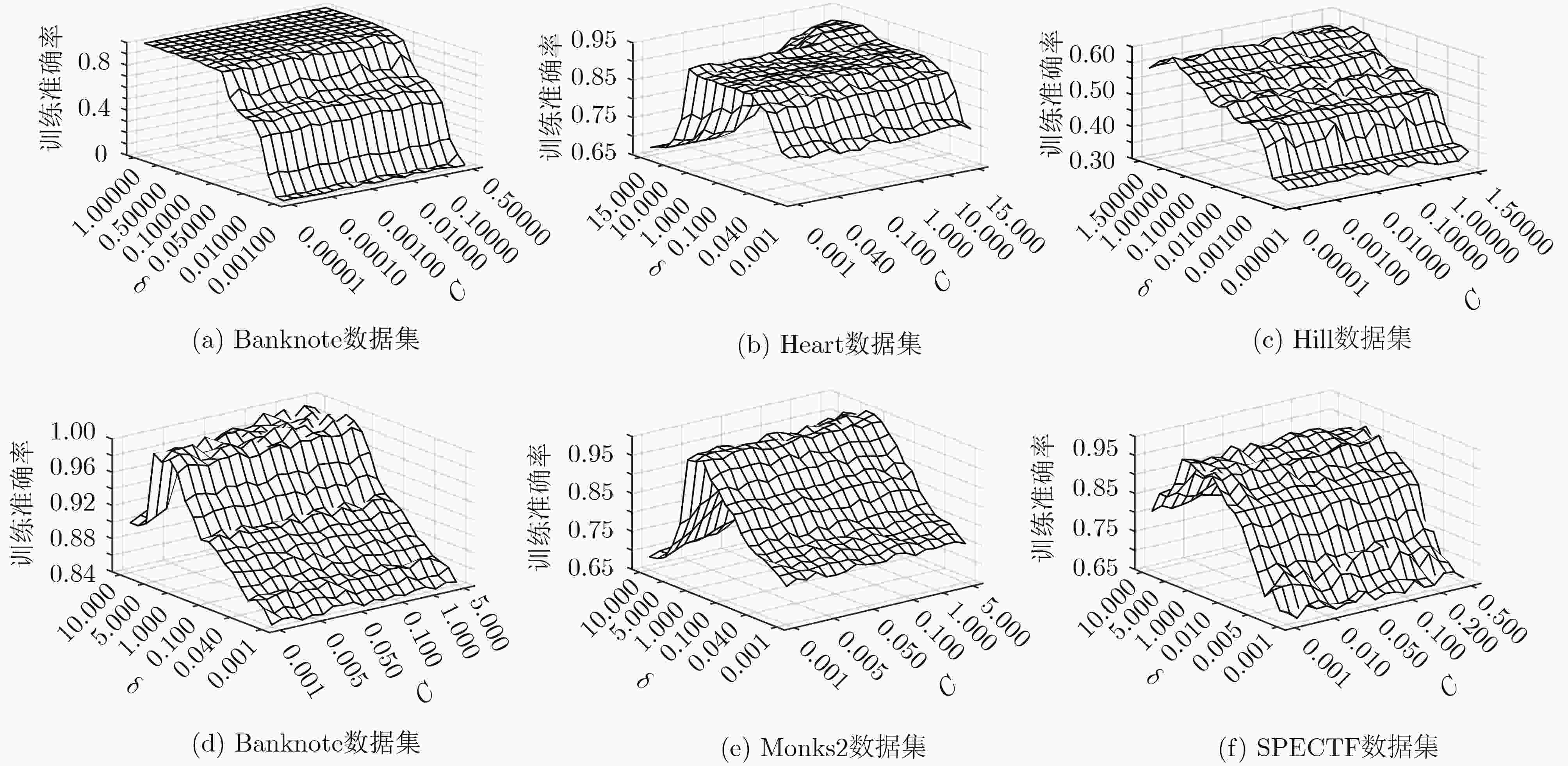
$ C{\text{和}}\delta $ 的格子搜索法近优组合值数据集 $C$ $\delta $ 数据集 $C$ $\delta $ Banknote 0.100 0.01 Debrecen 1.000 2.00 Fertility 0.005 0.01 Creditcard 1.000 10.00 Hill 0.010 0.10 Occupancy 0.500 5.00 Monks1 1.000 5.00 HTRU2 0.010 10.00 Monks2 0.500 2.00 Heart 10.000 5.00 SPECTF 0.010 2.00 Australian 10.000 5.00 Pdspeech 0.050 5.00 Liver 10.000 0.05 Epileptic 1.000 50.00 Ionosphere 0.010 1.00 Mushroom 0.010 0.10 Pima 0.100 0.01 Spambase 0.100 10.00 Cancer 0.500 2.00 Adult 10.000 5.00 Sonar 100.000 10.00 表 6 6种极限学习机算法分类精度比较(%)
数据集 BSADMM-KELM EKELM[16] TELM[17] $\upsilon {\rm{ - OELM}}$[18] Sparse ELM[19] LapTELM[20] Australian 90.72 85.22 75.14 68.20 72.49 75.51 Liver 76.95 71.51 76.96 72.41 – 72.10 Heart 88.74 – 83.15 76.00 70.74 76.09 Ionosphere 96.43 95.44 95.71 90.13 91.80 90.94 Pima 79.12 – 77.71 77.23 69.34 68.94 Cancer 96.58 97.36 – 96.58 94.25 – Sonar 95.58 89.40 91.49 78.80 68.50 85.68 -
[1] HUANG Guangbin, ZHU Qinyu, SIEW C K, et al. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1/3): 489–501. doi: 10.1016/j.neucom.2005.12.126 [2] QING Yuanyuan, ZENG Yijie, LI Yue, et al. Deep and wide feature based extreme learning machine for image classification[J]. Neurocomputing, 2020, 412: 426–436. doi: 10.1016/j.neucom.2020.06.110 [3] CHEN Xudong, YANG Haiyue, WUN Jhangshang, et al. Power load forecasting in energy system based on improved extreme learning machine[J]. Energy Exploration & Exploitation, 2020, 38(4): 1194–1211. doi: 10.1177/0144598720903797 [4] KHAN M A, ABBAS S, KHAN K M, et al. Intelligent forecasting model of COVID-19 novel coronavirus outbreak empowered with deep extreme learning machine[J]. Computers, Materials & Continua, 2020, 64(3): 1329–1342. doi: 10.32604/cmc.2020.011155 [5] MUTHUNAYAGAM M and GANESAN K. Cardiovascular disorder severity detection using myocardial anatomic features based optimized extreme learning machine approach[J]. IRBM, To be published. doi: 10.1016/j.irbm.2020.06.004 [6] WU Yu, ZHANG Yongshan, LIU Xiaobo, et al. A multiobjective optimization-based sparse extreme learning machine algorithm[J]. Neurocomputing, 2018, 317: 88–100. doi: 10.1016/j.neucom.2018.07.060 [7] ZHANG Yongshan, WU Jia, CAI Zhihua, et al. Memetic extreme learning machine[J]. Pattern Recognition, 2016, 58: 135–148. doi: 10.1016/j.patcog.2016.04.003 [8] PENG Yong, KONG Wanzeng, and YANG Bing. Orthogonal extreme learning machine for image classification[J]. Neurocomputing, 2017, 266: 458–464. doi: 10.1016/j.neucom.2017.05.058 [9] ZUO Bai, HUANG Guangbin, WANG Danwei, et al. Sparse extreme learning machine for classification[J]. IEEE Transactions on Cybernetics, 2014, 44(10): 1858–1870. doi: 10.1109/TCYB.2014.2298235 [10] GHADIMI E, TEIXEIRA A, SHAMES I, et al. Optimal parameter selection for the alternating direction method of multipliers (ADMM): Quadratic problems[J]. IEEE Transactions on Automatic Control, 2015, 60(3): 644–658. doi: 10.1109/TAC.2014.2354892 [11] LIU Yuanyuan, SHANG Fanhua, and CHENG J. Accelerated variance reduced stochastic ADMM[C].The Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, USA, 2017: 2287–2293. [12] DHAR S, YI Congrui, RAMAKRISHNAN N, et al. ADMM based scalable machine learning on Spark[C]. 2015 IEEE International Conference on Big Data (Big Data), Santa Clara, USA, 2015. [13] STELLATO B, BANJAC G, GOULART P, et al. OSQP: An operator splitting solver for quadratic programs[J]. Mathematical Programming Computation, 2020, 12(4): 637–672. doi: 10.1007/s12532-020-00179-2 [14] HUANG Guangbin, DING Xiaojian, and ZHOU Hongming. Optimization method based extreme learning machine for classification[J]. Neurocomputing, 2010, 74(1/3): 155–163. doi: 10.1016/j.neucom.2010.02.019 [15] HUYER W and NEUMAIER A. MINQ: General definite and bound constrained indefinite quadratic programming[EB/OL]. https://www.mat.univie.ac.at/~neum/software/minq/, 2017. [16] ZHANG Wenyu, ZHANG Zhenjiang, WANG Lifu, et al. Extreme learning machines with expectation kernels[J]. Pattern Recognition, 2019, 96: 106960. doi: 10.1016/j.patcog.2019.07.005 [17] WAN Yihe, SONG Shiji, HUANG Gao, et al. Twin extreme learning machines for pattern classification[J]. Neurocomputing, 2017, 260: 235–244. doi: 10.1016/j.neucom.2017.04.036 [18] DING Xiaojian, LAN Yuan, ZHANG Zhifeng, et al. Optimization extreme learning machine with ν regularization[J]. Neurocomputing, 2017, 261: 11–19. doi: 10.1016/j.neucom.2016.05.114 [19] YANG Liming and ZHANG Siyun. A sparse extreme learning machine framework by continuous optimization algorithms and its application in pattern recognition[J]. Engineering Applications of Artificial Intelligence, 2016, 53: 176–189. doi: 10.1016/j.engappai.2016.04.003 [20] LI Shuang, SONG Shiji, and WAN Yihe. Laplacian twin extreme learning machine for semi-supervised classification[J]. Neurocomputing, 2018, 321: 17–27. doi: 10.1016/j.neucom.2018.08.028 -






 下载:
下载:



 下载:
下载:
