Optimal Granularity Selection Method Based on Cost-sensitive Sequential Three-way Decisions
-
摘要: 最优粒度选择是序贯三支决策领域研究的热点之一,旨在通过合理的粒度选择来对复杂问题进行求解。在现阶段最优粒度选择中,代价敏感是影响决策的重要因素之一。针对这个问题,该文首先基于信息增益和卡方检验提出一种新的属性重要度计算方法;其次,为了更好地符合实际应用场景,在构建多粒度空间时将代价参数与粒度大小相结合,设置了相应的惩罚规则,并分析了决策阈值的变化规律;最后,为了消除测试代价和决策代价量纲不一致所带来的影响,借助变异系数设计了一种客观的代价计算方法。实验结果表明,该模型适用于现有代价认知场景,能在给定代价情况下选出代价最小的最优粒层。Abstract: Optimal granularity selection is one of the hotspots in the research of sequential three-way decisions. It aims to solve complex problems through reasonable granularity selection. At present, in the field of optimal granularity selection, cost sensitivity is one of the important factors affecting decision making. To solve this problem, firstly, based on information gain and chi-squared test, a novel method to measure the attribute significance is proposed when constructing the multi-granularity space in this paper. Then, to better conform the practical application, the corresponding penalty rule is set by combining the cost parameters and the granularity, and the variation rule of the decision threshold is analyzed. Finally, to eliminate the influence of the dimensional difference between the test cost and the decision cost, an objective cost calculation method is given by the coefficient of variation. The experimental results show that the proposed algorithm can be used in existing cost cognition scene, and the optimal granular layer with the lowest cost can be obtained under the given cost scene.
-
表 1 代价参数矩阵
$X$ ${}^\neg X$ ${a_P}$ 0 $\lambda _{{\rm{PN}}}^k$ ${a_B}$ $\lambda _{{\rm{BP}}}^k$ $\lambda _{{\rm{BN}}}^k$ ${a_N}$ $\lambda _{{\rm{NP}}}^k$ 0 表 2 数据集的描述
序号 数据集 属性特征 数目 条件属性个数 1 Balance-scale Categorical 625 4 2 Breast Cancer Wisconsin Integer 699 9 3 Tic-Tac-Toe Endgame Categorical 958 9 4 Car Evaluation Categorical 1728 6 5 Nursery Categorical 12960 8 6 Chess Categorical, Integer 28056 6 表 3 代价参数
${\lambda _{{\rm{PP}}}}$ ${\lambda _{{\rm{BP}}}}$ ${\lambda _{{\rm{NP}}}}$ ${\lambda _{{\rm{PN}}}}$ ${\lambda _{{\rm{BN}}}}$ ${\lambda _{{\rm{NN}}}}$ 第1组 0 1 4 5 2 0 第2组 0 2 6 7 3 0 表 4 第1组代价参数下各个数据集最优粒层信息
数据集 最优粒层 测试代价 决策代价 权重 总代价 Balance-scale 3 696.6 118.0 (0.46,0.54) 0.4172 Breast Cancer Wisconsin 8 323.7 522.6 (0.52,0.48) 0.3684 Tic-Tac-Toe Endgame 6 424.0 314.3 (0.49,0.51) 0.4453 Car Evaluation 4 636.0 35.2 (0.52,0.48) 0.4032 Chess 4 1997.3 0.0 (0.50,0.50) 0.4818 Nursery 6 998.9 8677.1 (0.54,0.46) 0.5423 表 5 第2组代价参数下每个数据集最优粒层信息
数据集 最优粒层 测试代价 决策代价 权重 总代价 Balance-scale 3 696.6 73.0 (0.47,0.53) 0.3172 Breast Cancer Wisconsin 5 227.9 652.1 (0.48,0.52) 0.4459 Tic-Tac-Toe Endgame 6 424.0 147.4 (0.40,0.60) 0.2941 Car Evaluation 4 636.0 372.1 (0.42,0.58) 0.3132 Chess 4 1997.3 14029.1 (0.41,0.59) 0.3705 Nursery 5 731.3 17162.085 (0.55,0.45) 0.5522 表 6 最优粒层比较
数据集 模型 最优粒层 冗余属性 最优属性子集 Balance-scale 模型1 3 $\phi $ $\{ {c_4},{c_3},{c_2}\} $ 模型2 3 $\phi $ $\{ {c_4},{c_3},{c_2}\} $ Breast Cancer Wisconsin 模型1 8 $\{ {c_1}\} $ $\{ {c_2},{c_3},{c_6},{c_7},{c_5},{c_8},{c_4},{c_9}\} $ 模型2 5 $\{ {c_1}\} $ $\{ {c_2},{c_3},{c_6},{c_7},{c_5}\} $ Tic-Tac-Toe Endgame 模型1 6 $\phi $ $\{ {c_8},{c_6},{c_4},{c_2},{c_9},{c_7}\} $ 模型2 6 $\phi $ $\{ {c_8},{c_6},{c_4},{c_2},{c_9},{c_7}\} $ Car Evaluation 模型1 3 $\{ {c_2}\} $ $\{ {c_4},{c_1},{c_6}\} $ 模型2 3 $\{ {c_2}\} $ $\{ {c_4},{c_1},{c_6}\} $ Chess 模型1 6 $\phi $ $\{ {c_3},{c_5},{c_2},{c_1},{c_4},{c_6}\} $ 模型2 5 $\phi $ $\{ {c_3},{c_5},{c_2},{c_1},{c_4}\} $ Nursery 模型1 6 $\{ {c_3},{c_6}\} $ $\{ {c_8},{c_2},{c_1},{c_7},{c_5},{c_4}\} $ 模型2 6 $\{ {c_3},{c_6}\} $ $\{ {c_8},{c_2},{c_1},{c_7},{c_5},{c_4}\} $ -
[1] LIAO Shujiao, ZHU Qingxin, QIAN Yuhua, et al. Multi-granularity feature selection on cost-sensitive data with measurement errors and variable costs[J]. Knowledge-Based Systems, 2018, 158: 25–42. doi: 10.1016/j.knosys.2018.05.020 [2] YANG Jie, WANG Guoyin, ZHANG Qinghua, et al. Optimal granularity selection based on cost-sensitive sequential three-way decisions with rough fuzzy sets[J]. Knowledge-Based Systems, 2019, 163: 131–144. doi: 10.1016/j.knosys.2018.08.019 [3] LI Huaxiong, ZHANG Libo, ZHOU Xianzhong, et al. Cost-sensitive sequential three-way decision modeling using a deep neural network[J]. International Journal of Approximate Reasoning, 2017, 85: 68–78. doi: 10.1016/j.ijar.2017.03.008 [4] ZHANG Yanping, ZOU Huijin, CHEN Xi, et al. Cost-sensitive three-way decisions model based on CCA[C]. The 9th International Conference on Rough Sets and Current Trends in Computing, Granada and Madrid, Spain, 2014: 172–180. doi: 10.1007/978-3-319-08644-6_18. [5] JIA Xiuyi, LIAO Wenhe, TANG Zhenmin, et al. Minimum cost attribute reduction in decision-theoretic rough set models[J]. Information Sciences, 2013, 219: 151–167. doi: 10.1016/j.ins.2012.07.010 [6] YANG Xibei, QI Yunsong, SONG Xiaoning, et al. Test cost sensitive multigranulation rough set: Model and minimal cost selection[J]. Information Sciences, 2013, 250: 184–199. doi: 10.1016/j.ins.2013.06.057 [7] MIN Fan and LIU Qihe. A hierarchical model for test-cost-sensitive decision systems[J]. Information Sciences, 2009, 179(14): 2442–2452. doi: 10.1016/j.ins.2009.03.007 [8] JU Hengrong, LI Huaxiong, YANG Xibei, et al. Cost-sensitive rough set: A multi-granulation approach[J]. Knowledge-Based Systems, 2017, 123: 137–153. doi: 10.1016/j.knosys.2017.02.019 [9] JU Hengrong, YANG Xibei, YU Hualong, et al. Cost-sensitive rough set approach[J]. Information Sciences, 2016, 355/356: 282–298. doi: 10.1016/j.ins.2016.01.103 [10] YAO Yiyu and DENG Xiaofei. Sequential three-way decisions with probabilistic rough sets[C]. IEEE 10th International Conference on Cognitive Informatics and Cognitive Computing (ICCI-CC’11), Banff, Canada, 2011: 120–125. doi: 10.1109/COGINF.2011.6016129. [11] ZHANG Qinghua, CHEN Yuhong, YANG Jie, et al. Fuzzy entropy: A more comprehensible perspective for interval shadowed sets of fuzzy sets[J]. IEEE Transactions on Fuzzy Systems, 2020, 28(11): 3008–3022. doi: 10.1109/tfuzz.2019.2947224 [12] ZHANG Qinghua, ZHAO Fan, YANG Jie, et al. Three-way decisions of rough vague sets from the perspective of fuzziness[J]. Information Sciences, 2020, 523: 111–132. doi: 10.1016/j.ins.2020.03.013 [13] 张清华, 幸禹可, 周玉兰. 基于粒计算的增量式知识获取方法[J]. 电子与信息学报, 2011, 33(2): 435–441. doi: 10.3724/SP.J.1146.2010.00217ZHANG Qinghua, XING Yuke, and ZHOU Yulan. The incremental knowledge acquisition algorithm based on granular computing[J]. Journal of Electronics &Information Technology, 2011, 33(2): 435–441. doi: 10.3724/SP.J.1146.2010.00217 [14] FANG Yu, GAO Cong, and YAO Yiyu. Granularity-driven sequential three-way decisions: A cost-sensitive approach to classification[J]. Information Sciences, 2020, 507: 644–664. doi: 10.1016/j.ins.2019.06.003 [15] LI Huaxiong, ZHANG Libo, HUANG Bing, et al. Sequential three-way decision and granulation for cost-sensitive face recognition[J]. Knowledge-Based Systems, 2016, 91: 241–251. doi: 10.1016/j.knosys.2015.07.040 [16] QIAN Jin, LIU Caihui, MIAO Duoqian, et al. Sequential three-way decisions via multi-granularity[J]. Information Sciences, 2020, 507: 606–629. doi: 10.1016/j.ins.2019.03.052 [17] 陈泽华, 马贺. 基于粒矩阵的多输入多输出真值表快速并行约简算法[J]. 电子与信息学报, 2015, 37(5): 1260–1265. doi: 10.11999/JEIT141129CHEN Zehua and MA He. Granular matrix based rapid parallel reduction algorithm for MIMO truth table[J]. Journal of Electronics &Information Technology, 2015, 37(5): 1260–1265. doi: 10.11999/JEIT141129 [18] ZHANG Qinghua, XIA Deyou, and WANG Guoyin. Three-way decision model with two types of classification errors[J]. Information Sciences, 2017, 420: 431–453. doi: 10.1016/j.ins.2017.08.066 [19] 王国胤. Rough集理论与知识获取[M]. 西安: 西安交通大学出版社, 2001: 17–18. [20] PAWLAK Z. Rough sets[J]. International Journal of Computer & Information Sciences, 1982, 11(5): 341–356. doi: 10.1007/BF01001956 [21] PLACKETT R L. Karl Pearson and the chi-squared test[J]. International Statistical Review, 1983, 51(1): 59–72. doi: 10.2307/1402731 [22] 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 75. [23] QUINLAN J R. Induction of decision trees[J]. Machine Learning, 1986, 1(1): 81–106. doi: 10.1023/A:1022643204877 [24] LIU Dun, LI Tianrui, and LIANG Decui. Three-way decisions in dynamic decision-theoretic rough sets[C]. The 8th International Conference on Rough Sets and Knowledge Technology, Halifax, Canada, 2013: 291–301. doi: 10.1007/978-3-642-41299-8_28. -





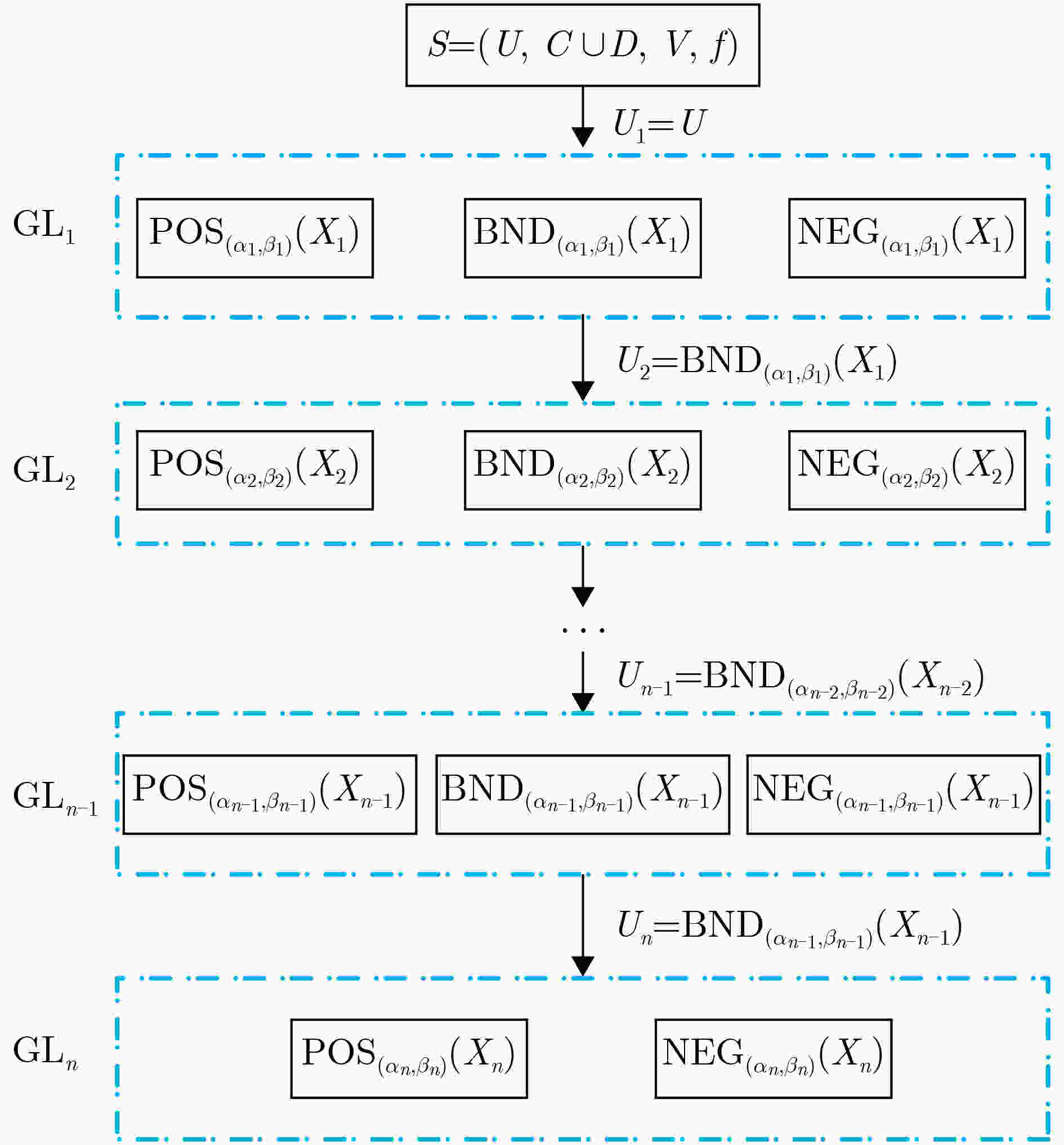
 下载:
下载:
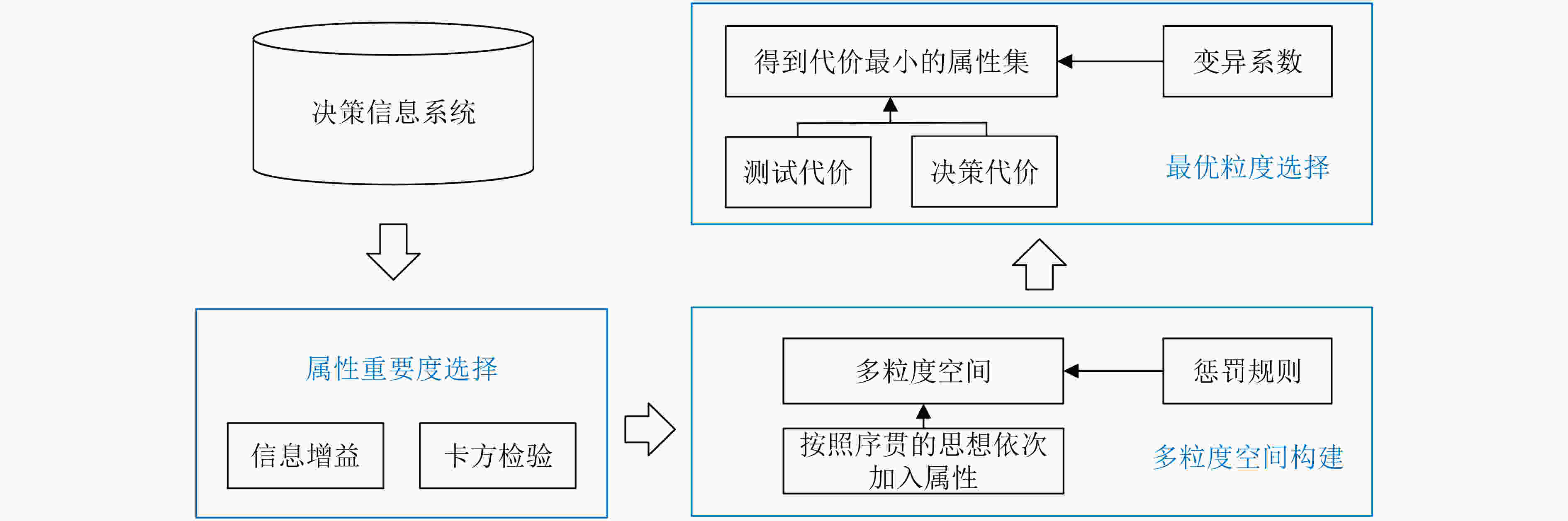
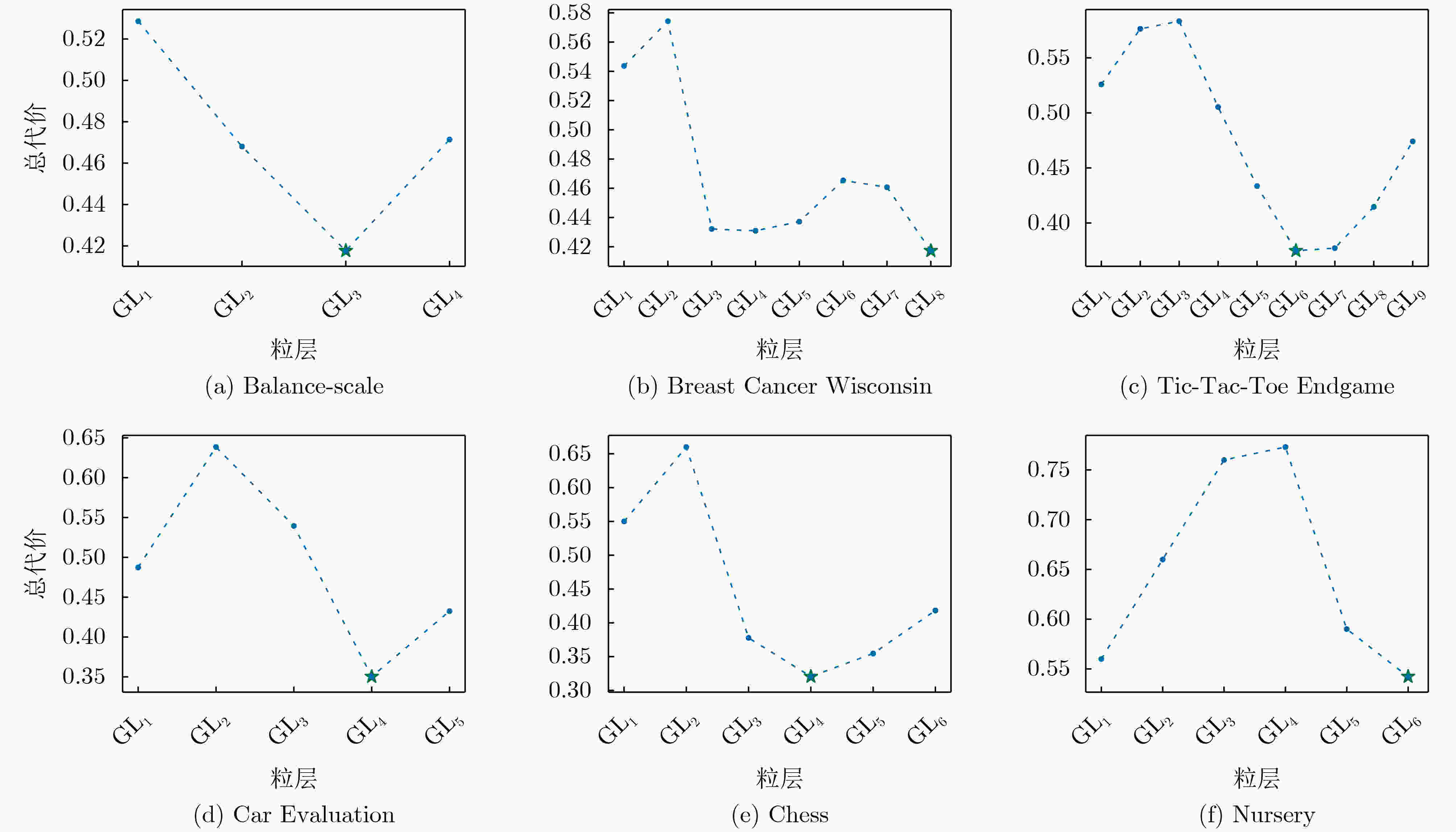
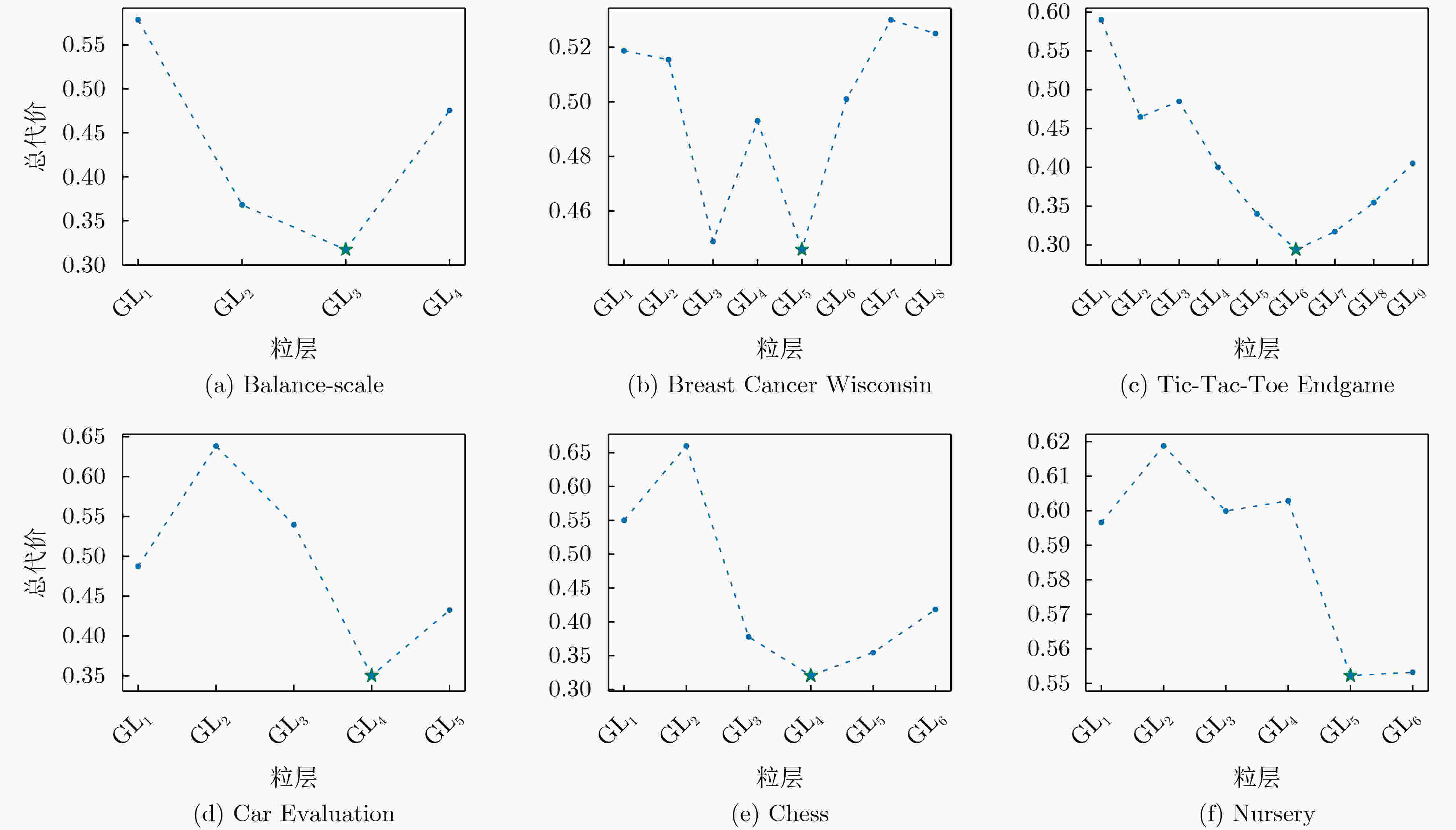


 下载:
下载:
