| [1] |
SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830
|
| [2] |
ROY R and KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 984–995. doi: 10.1109/29.32276
|
| [3] |
MALIOUTOV D, CETIN M, and WILLSKY A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Transactions on Signal Processing, 2005, 53(8): 3010–3022. doi: 10.1109/TSP.2005.850882
|
| [4] |
蒋莹, 王冰切, 韩俊, 等. 基于分布式压缩感知的宽带欠定信号DOA估计[J]. 电子与信息学报, 2019, 41(7): 1690–1697. doi: 10.11999/JEIT180723JIANG Ying, WANG Bingqie, HAN Jun, et al. Underdetermined wideband DOA estimation based on distributed compressive sensing[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1690–1697. doi: 10.11999/JEIT180723
|
| [5] |
WU Xiaohuan, ZHU Weiping, and YAN Jun. Direction of arrival estimation for off-grid signals based on sparse bayesian learning[J]. IEEE Sensors Journal, 2016, 16(7): 2004–2016. doi: 10.1109/JSEN.2015.2508059
|
| [6] |
CHEN Peng, CAO Zhenxin, CHEN Zhimin, et al. Sparse off-grid DOA estimation method with unknown mutual coupling effect[J]. Digital Signal Processing, 2019, 90: 1–9. doi: 10.1016/j.dsp.2019.04.001
|
| [7] |
CHEN Peng, CHEN Zhimin, CAO Zhenxin, et al. A new atomic norm for DOA estimation with gain-phase errors[J]. IEEE Transactions on Signal Processing, 2020, 68: 4293–4306. doi: 10.1109/TSP.2020.3010749
|
| [8] |
ZHU Hao, LEUS G, and GIANNAKIS G. Sparsity-cognizant total least-squares for perturbed compressive sampling[J]. IEEE Transactions on Signal Processing, 2011, 59(5): 2002–2016. doi: 10.1109/TSP.2011.2109956
|
| [9] |
YANG Zai, ZHANG Cishen, and XIE Lihua. Robustly stable signal recovery in compressed sensing with structured matrix perturbation[J]. IEEE Transactions on Signal Processing, 2012, 60(9): 4658–4671. doi: 10.1109/TSP.2012.2201152
|
| [10] |
YANG Zai, XIE Lihua, and ZHANG Cishen. Off-grid direction of arrival estimation using sparse Bayesian inference[J]. IEEE Transactions on Signal Processing, 2013, 61(1): 38–43. doi: 10.1109/TSP.2012.2222378
|
| [11] |
WU Xiaohuan, ZHU Weiping, YAN Jun, et al. Two sparse-based methods for off-grid direction-of-arrival estimation[J]. Signal Processing, 2018, 142: 87–95. doi: 10.1016/j.sigpro.2017.07.004
|
| [12] |
BJÖRNSON E, SANGUINETTI L, WYMEERSCH H, et al. Massive MIMO is a reality - what is next?: five promising research directions for antenna arrays[J]. Digital Signal Processing, 2019, 94: 3–20. doi: 10.1016/j.dsp.2019.06.007
|
| [13] |
HE J, SWAMY M N S, and AHMAD M. Efficient application of MUSIC algorithm under the coexistence of far-field and near-field sources[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 2066–2070. doi: 10.1109/TSP.2011.2180902
|
| [14] |
LIANG Junli and LIU Ding. Passive localization of mixed near-field and far-field sources using two-stage MUSIC algorithm[J]. IEEE Transactions on Signal Processing, 2010, 58(1): 108–120. doi: 10.1109/TSP.2009.2029723
|
| [15] |
WANG Bo, LIU Juanjuan, and SUN Xiaoying. Mixed sources localization based on sparse signal reconstruction[J]. IEEE Signal Processing Letters, 2012, 19(8): 487–490. doi: 10.1109/lsp.2012.2204248
|





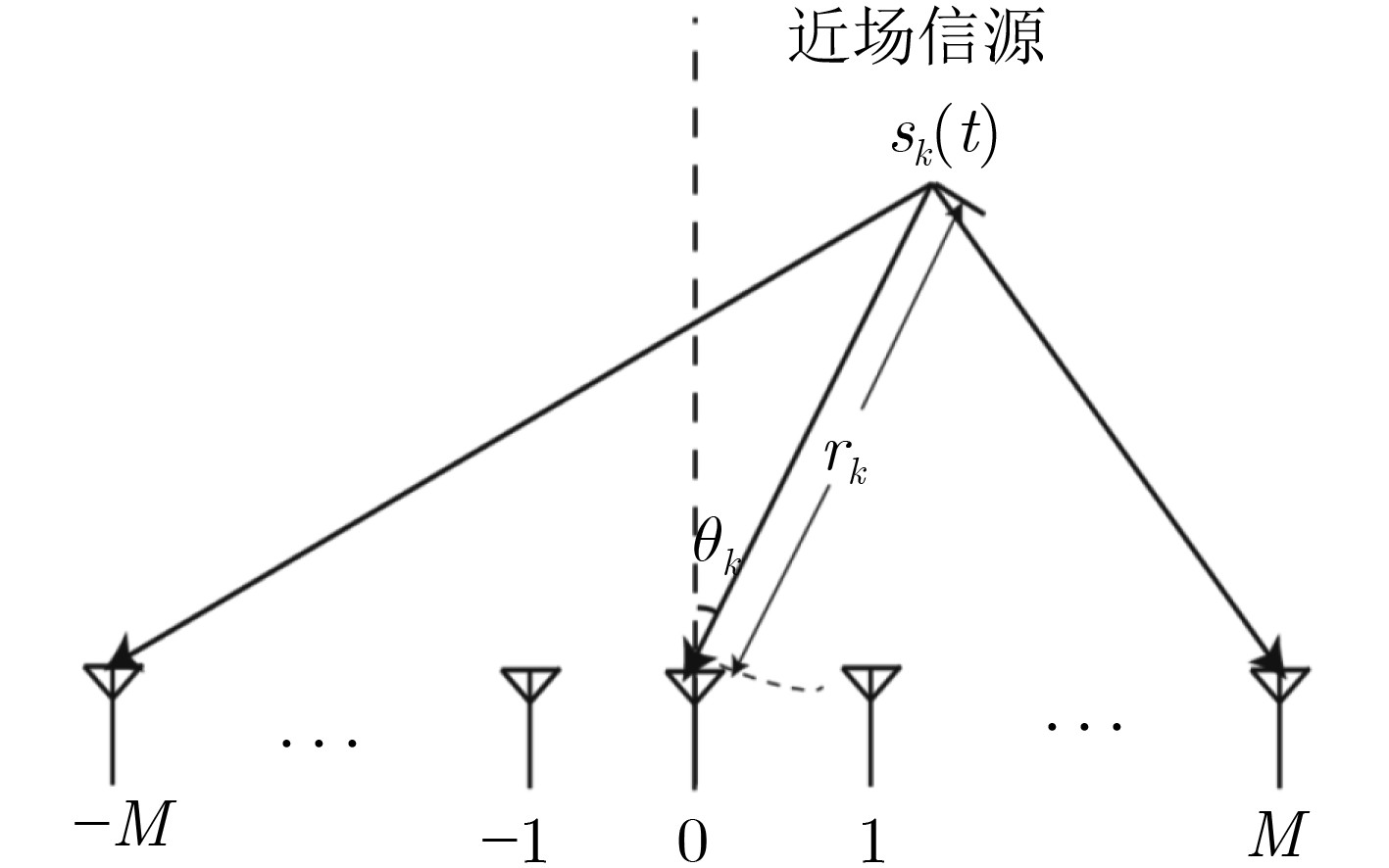
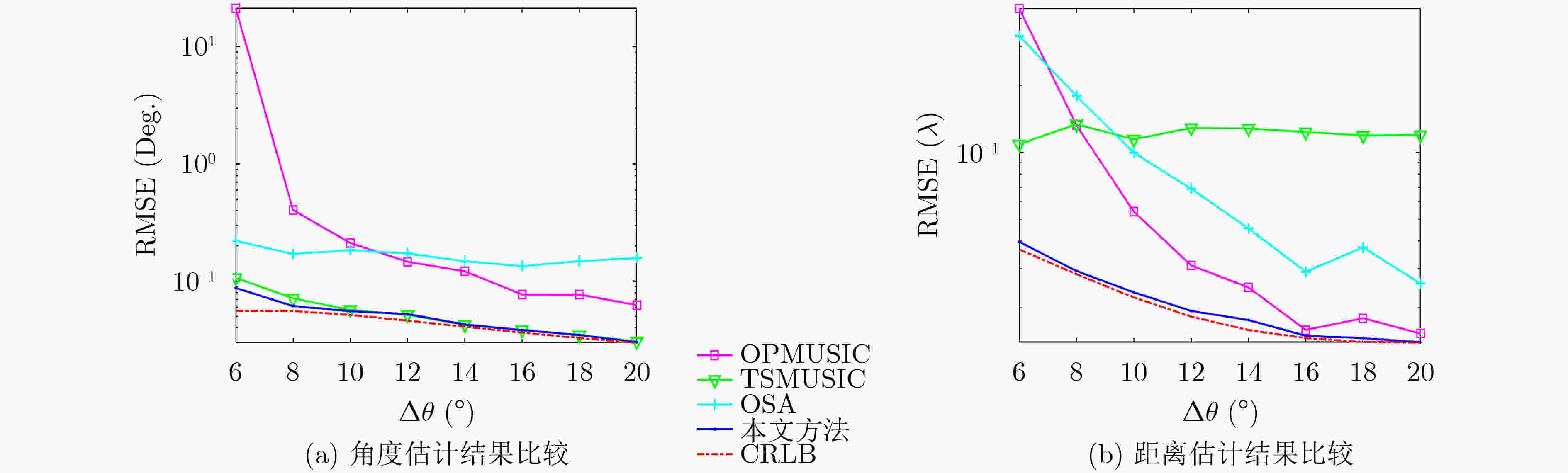
 下载:
下载:
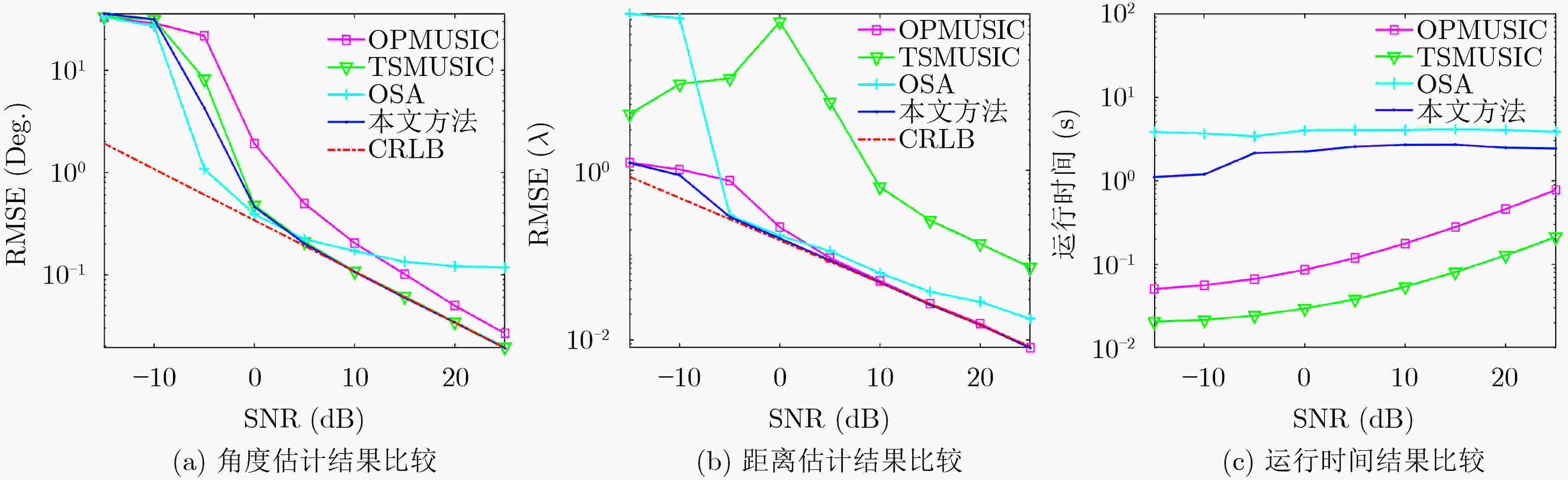
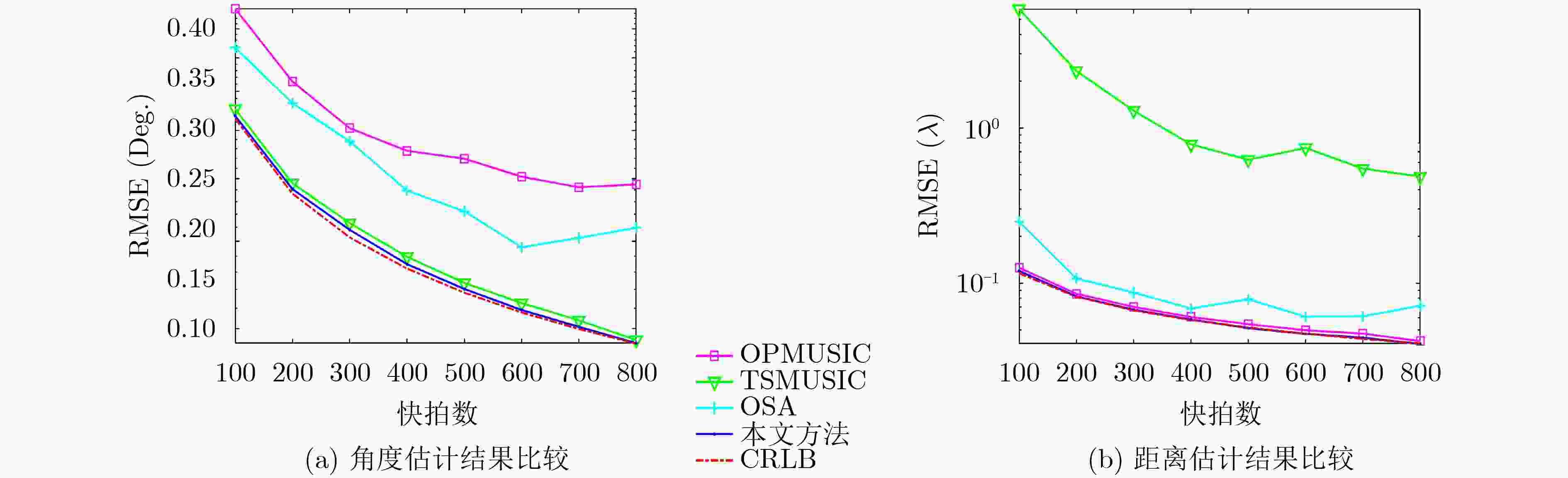
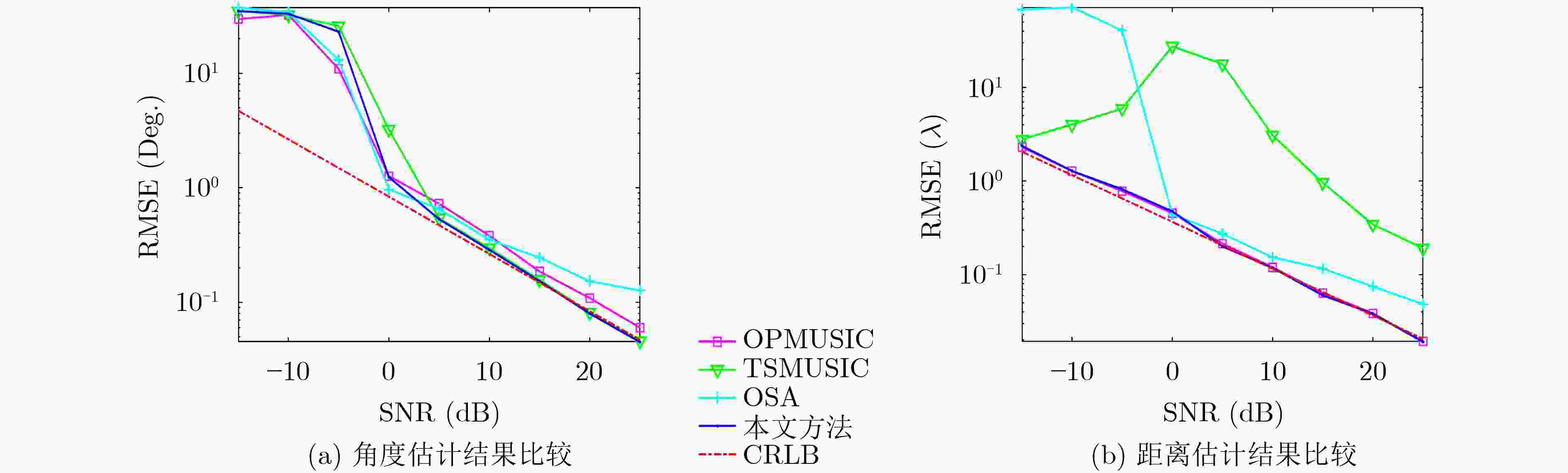


 下载:
下载:
