A General Method of Generating Code Density Calibration Signal for Time-to-Digital Converter and Its Realization
-
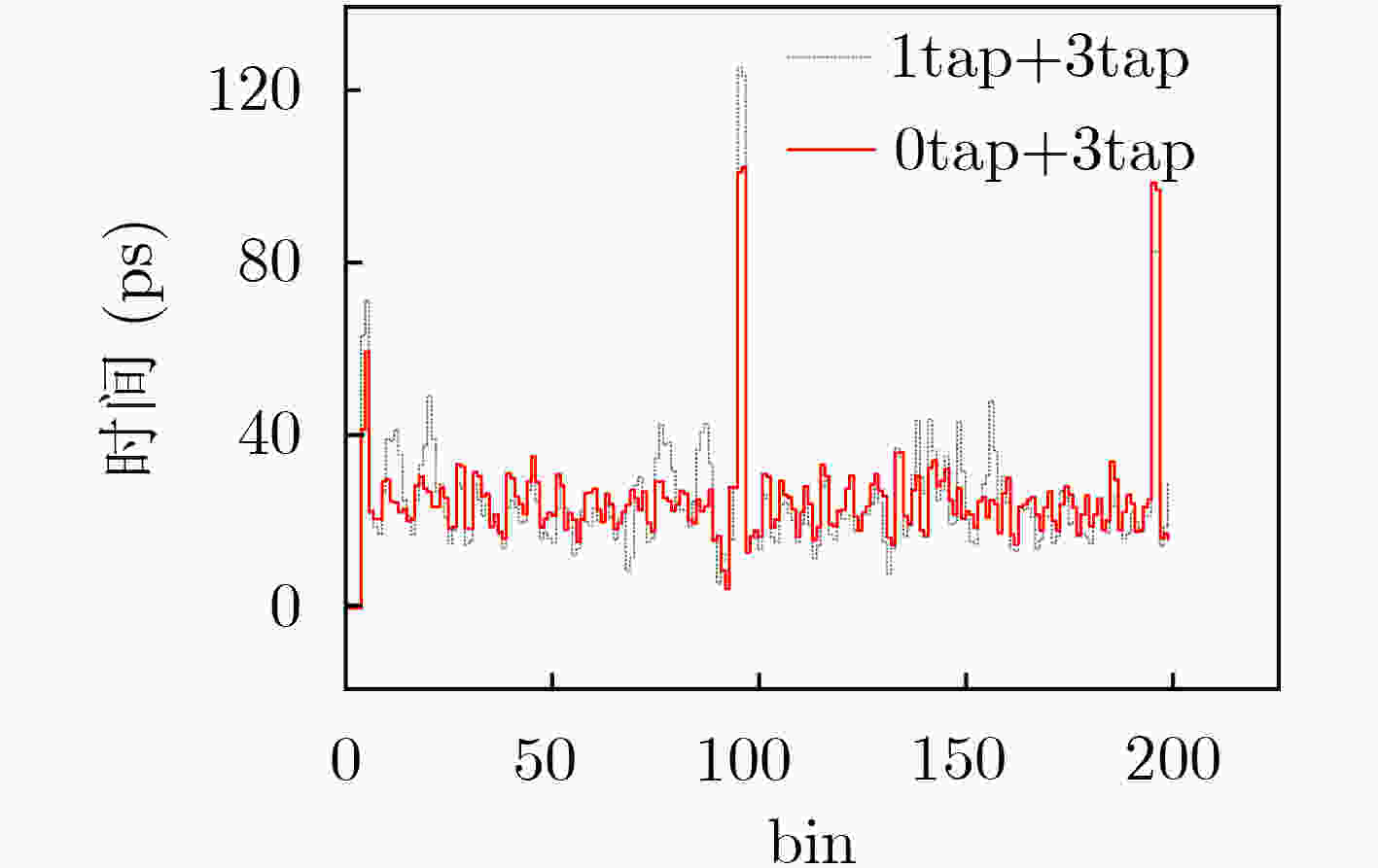
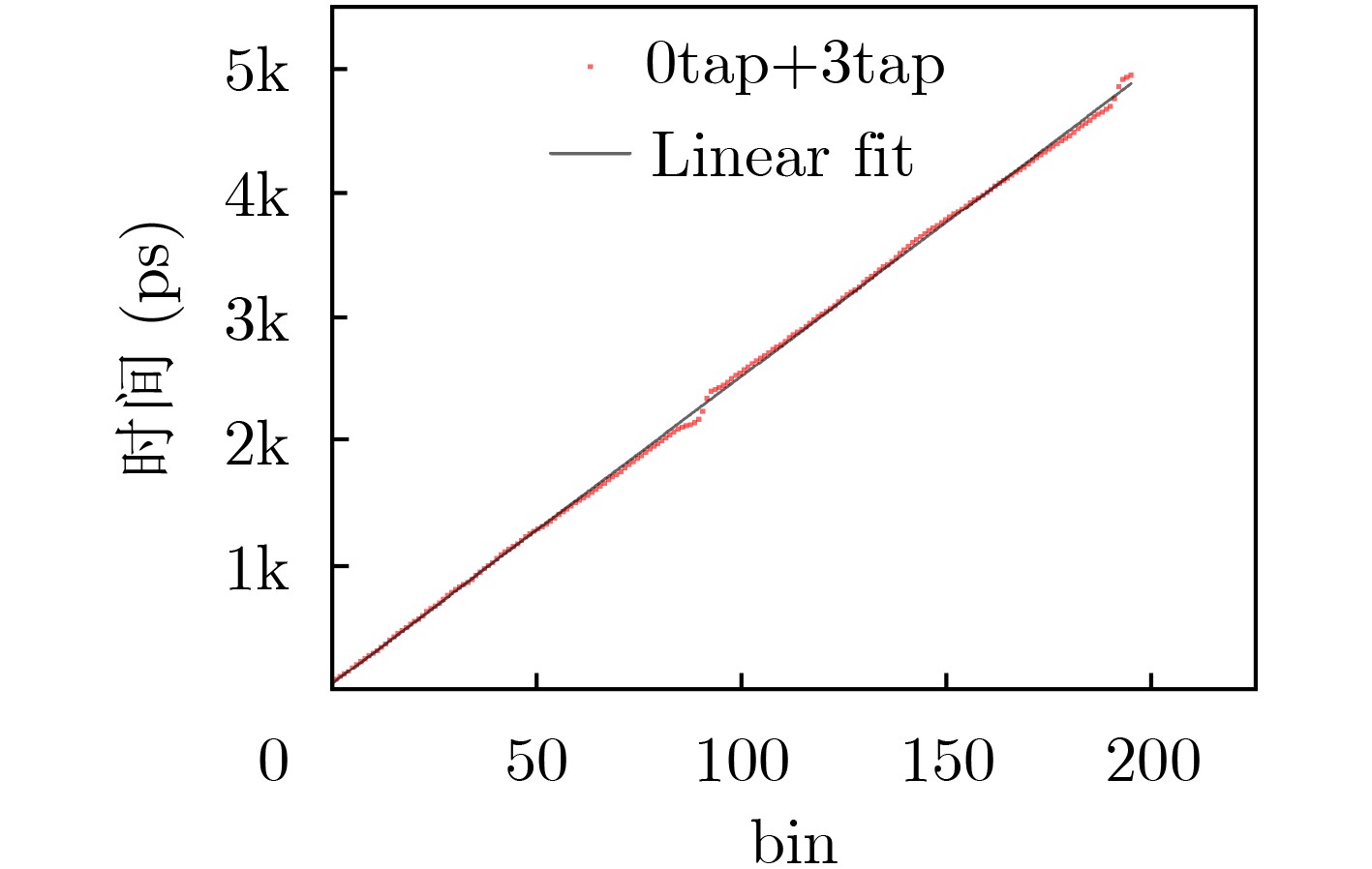
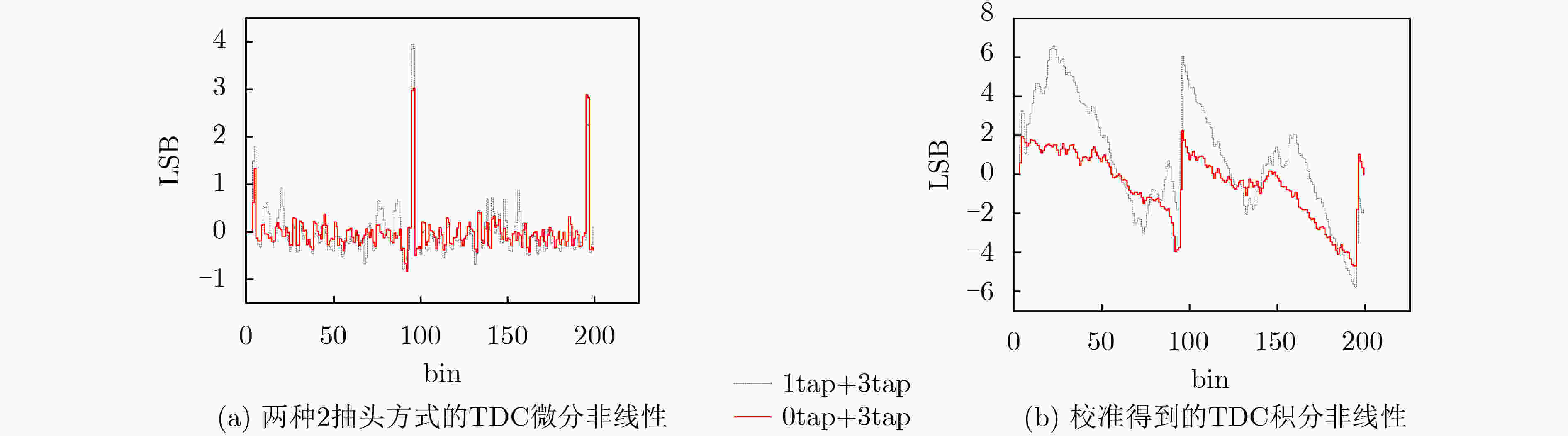
摘要: 该文提出一种通用的时间数字转换器(TDC)码密度校准信号产生方法，该方法基于相干采样理论，通过合理设置TDC主时钟和校准信号之间的频率差，结合输出信号保持电路，产生校准用的随机信号，在码密度校准过程中，随机信号均匀分布在TDC的延时路径上，实现对TDC的bin-by-bin校准。基于Xilinx公司的28 nm工艺的Kintex-7 现场可编程门阵列(FPGA)内部的进位链实现一种plain TDC，利用该方法校准plain TDC的码宽(抽头延迟时间)，研究校准了2抽头方式下的TDC的性能参数，时间分辨率(对应TDC的最低有效位，Least Significant Bit, LSB)为24.9 ps，微分非线性为(–0.84～3.1)LSB，积分非线性为(–5.0～2.2)LSB。文中所述的校准方法采用时钟逻辑资源实现，多次测试考核结果表明，单个延时单元的标准差优于0.5 ps。该校准方法采用时钟逻辑资源代替组合逻辑资源，重复性、稳定性较好，实现了对plain TDC的高精度自动校准。该方法同样适用于其他类型的TDC的码密度校准。Abstract: This paper proposes a universal Time-to-Digital Converter (TDC) code density calibration signal generation method, which is based on the theory of coherent sampling. By reasonably setting the frequency difference between the TDC master clock and the calibration signal, combining with the output hold circuit, a random signal for calibration is generated to ensure that the random signal is evenly distributed on the TDC delay path to achieve Bin-by-bin calibration of TDC. The paper implements a carry chain plain TDC based on XILINX’s 28 nm Kintex-7 Field Programmable Gate Array (FPGA). The method is used to calibrate the code width (tap delay time) of plain TDC, and the performance parameters of TDC in 2-tap mode are studied and calibrated. The time resolution (corresponding to the least significant bit of TDC, Least Significant Bit, LSB) is 24.9 ps, with the differential nonlinearity is (–0.84～3.1) LSB, and the integral nonlinearity is (–5.0～2.2) LSB. The calibration method described in the paper is implemented using clock logic resources, and multiple tests show that the standard deviation of a single delay unit is better than 0.5 ps. This calibration method uses clock logic resources instead of combinatorial logic resources to realize high-precision automatic calibration of plain TDC, with good repeatability and stability. This method is also suitable for other types of TDC code density calibration.
-
1. 引言
时间作为物理学中7个基本物理量之一，在物理学的发展中起着至关重要的作用，精确获取研究对象的时间信息具有重要的意义。对时间信息的获取可以由时间数字转换器(Time to Digital Converter, TDC)来实现，TDC将时间间隔转换为二进制数字编码，输出到后端分析得到具体的时间信息。TDC广泛应用在高能物理、导航定位、卫星授时、数字通信、医学成像等众多领域，特别是在高能物理实验中[1,2]，TDC获取的时间信息能够间接反映粒子的动量、质量等信息，对鉴别粒子种类、诊断粒子反应过程等有很重要的作用。
TDC有多种实现方法，包括时间间隔扩展法、时间幅度转换法、直接计数法、时钟分相法、游标法、抽头延迟链法和差分延迟链法等；各种方法可以独立使用，也可以配合使用，可以实现从普通精度到高精度、从粗时间到细时间的时间间隔测量。从实现方法上来看，TDC的实现方法可以分为模拟方法和数字方法；从实现平台上看，TDC可以在专用集成电路(Application Specific Integrated Circuit, ASIC)、现场可编程门阵列(Field Programmable Gate Array, FPGA)等平台上实现。ASIC-TDC的测量精度和稳定性更高，但是，ASIC-TDC都是针对某一具体应用设计，不具有普适性，并且开发一款ASIC芯片周期很长；FPGA-TDC具有开发周期短、集成度高、成本低、设计灵活等优点，但是其非线性较差。
随着微电子技术、半导体制造工艺的发展，FPGA-TDC的测量精度、稳定性等同步提高，在FPGA上实现高精度TDC具有重要研究意义。目前，基于FPGA实现的高精度TDC的研究主要集中在几个方面：(1) TDC的实现，基于FPGA内部资源实现高精度TDC，把时间信息转换成二进制编码，通过查找表输出至后端；(2) TDC的自动校准，选择合适的校准方法，校准TDC的码宽(bin size)，降低FPGA制造工艺、工作电压、工作温度(Process Voltage Temperature, PVT)等参数对TDC性能的影响；(3)针对TDC内部bin size的不一致性，如何平均化超宽bin，降低测量误差，进一步提高测试精度，单链多次平均测量(Wave Union, Ripple method)、多链单次平均测量等方法可以在已有工艺的基础上，尽可能改善FPGA-TDC的非线性，提高测量精度；(4)其他特殊功能，如动态监测并实时校准TDC的bin size，多通道TDC集成使用，针对特殊要求(如航天等)进行TDC的冗余设计等。
论文主要研究FPGA-TDC的自动校准方法，给出码密度校准方法的误差公式，分析了两种常用码密度校准信号产生方法，提出了一种基于相干采样理论的通用TDC码密度校准方法，通过合理设置TDC主时钟和校准信号之间的频率差，结合输出保持电路，产生校准用的随机信号，确保在码密度校准过程中，随机信号均匀分布在TDC的延时路径上，实现对TDC的逐位(bin-by-bin)校准。
2. TDC校准方法
TDC的常用校准方法主要分为平均校准和逐位校准两种[3-5]。平均校准可以对TDC进行快速校准，但是，得到的只是所有延迟单元抽头的平均延迟时间，无法对TDC中每个延迟单元抽头进行逐位校准，会导致较大的测量误差。逐位校准可以对级联延迟链中每一个延迟单元抽头进行bin-by-bin校准，一般通过码密度方法实现，可以精确标定每个延迟单元抽头的延迟时间。
根据文献[1]研究结果，在使用码密度校准方法校准TDC的码宽时，为了尽可能降低延迟单元的时间误差，需要增加校准次数，增加校准次数就会增加校准时间、增加资源占用量；使用时需要根据TDC指标要求折中考虑。在校准信号和TDC主时钟无关的前提下，认为校准信号是随机信号，标准差和校准次数之间的关系式如式(1)所示，式中，N为校准次数，k为级联链抽头数目，T为TDC主时钟周期，T=5 ns，抽头延时选择码宽的中间值，σi为第i个延迟单元的标准差，στ为校准误差最大值。根据式(1)，已知文章实现的校准次数为1000000次，对应TDC的校准误差最大值小于5 ps；同理，如果校准次数达到100000000次，对应TDC的校准误差最大值小于0.5ps。从另一个角度分析，如果以5 ps步进延时对TDC进行校准，那么1000000次校准，总步进时间为5 μs，相当于对5 ns周期的时钟遍历1000次，且遍历点不重复。
στ=TN√k∑i=1σ2i+σ2i2<T√N√1−1k<T√N (1) 校准信号产生：在游标法实现的TDC中，给出了一种典型的起振电路，该电路利用了FPGA内部的寄存器和门电路等资源，构造了可控的数字振荡电路如图1所示[2]，当复位为‘0’，脉冲为‘0’时，电路输出为‘0’，处于稳定状态；当复位为‘0’，脉冲发生0–1跳变时，系统开始起振，电路输出为周期振荡波形，处于振荡状态，震荡周期值为门电路总延时；当复位发生0–1跳变时，振荡状态结束，电路输出为‘0’，回到稳定状态。这种电路结构简单，门电路的延时一般在亚纳秒量级，可以产生高频的振荡信号，通过改变信号的传输链路可以调节振荡频率；缺点是产生的振荡信号受外界因素干扰明显、振荡频率不稳定且抖动较大。一般来说，码密度校准方法的校准次数较多，在一定程度上可以通过平均的方法降低这种抖动的影响。
文献[1]给出了一种利用FPGA内部的查找表(Look-Up Table, LUT)资源，通过级联查找表建立环形振荡电路的方法。环形振荡电路一般由奇数个反相器级联而成，将最后一个反相器输出反馈到第一个反相器输入可以形成环形结构，达到振荡的目的。FPGA是基于查找表结构建立，拥有大量查找表资源且方便级联，可以通过配置查找表来实现反相器的功能[6]。由查找表LUT1, LUT2构成的环形振荡器如图2所示，总共包含一个LUT2和偶数个LUT1, LUT1, LUT2的真值表如表1，表2所示，通过配置LUT2内部存储值为“0010”，当EN为‘0’时，LUT2不受I0影响，输出始终为‘0’；当EN为‘1’时，LUT2的输出O与输入I0反向，实现反相器功能；通过配置LUT1的内部存储值为“10”，实现反相器的功能。在校准过程中，EN为‘1’时，由查找表LUT1与LUT2组成的环形结构，相当于奇数个反相器组成的环形振荡电路；在测量或者待机时，为降低功耗、降低干扰，EN为‘0’，由查找表LUT1与LUT2组成的环形结构，相当于偶数个反相器，不形成振荡。
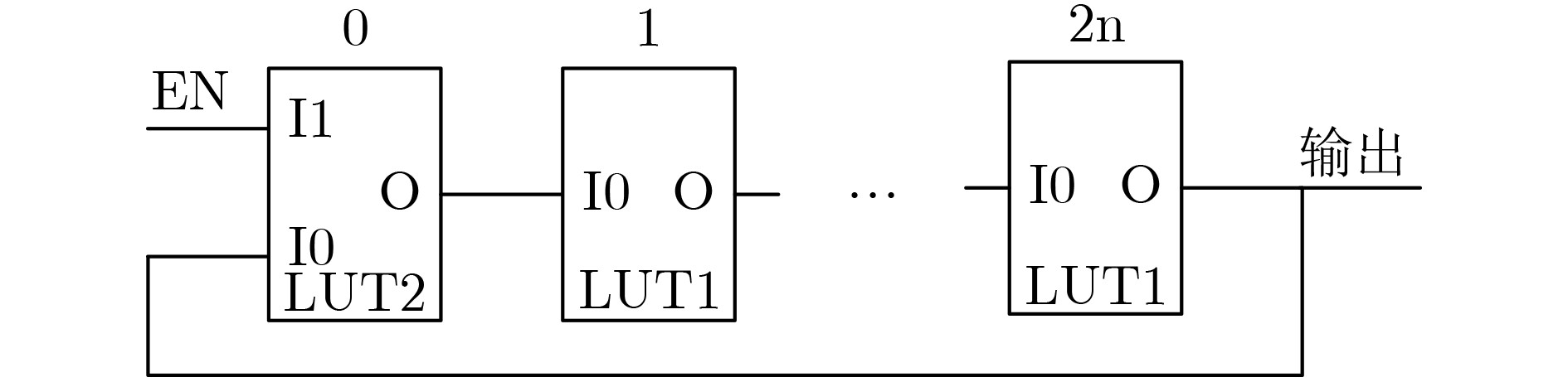
表 1 LUT1真值表I0 O 0 1 1 0 表 2 LUT2真值表I1 I0 O 0 0 0 0 1 0 1 0 1 1 1 0 3. 一种新的校准信号产生方法
前述的输出振荡信号作为校准信号的方法，采用FPGA内部的组合逻辑资源，基于自激振荡原理产生可控周期振荡，一般认为产生的校准信号与TDC主时钟无关，是随机信号。在码密度校准过程中，如果校准次数足够多，认为随机信号近似均匀分布在TDC的延时路径上，可以实现对TDC的高精度校准。
TDC的码密度测试与ADC的码密度测试原理类似，区别在于ADC的码密度测试是对幅值随机的模拟信号进行量化统计分析，以标定ADC的输出数字编码的非线性；TDC的码密度测试是对时间随机的数字信号进行量化统计分析，以标定TDC的延迟单元的非线性。在对ADC进行动态性能分析时，需要对正弦波采样数据进行傅里叶分析，如果ADC采样时钟和待采样正弦波频率满足严格的相干采样条件，那么在进行傅里叶分析时，采样信号的频谱就不会出现泄漏现象；否则，采样信号的频谱会泄漏，主要原因之一就是ADC采样的正弦波数据是非相干的，采样数据点有重复。理论上相干采样可以保证ADC采样的正弦波数据之间没有重复的，如果采样数据量足够大，相干采样可以保证采样数据点等效在一个正弦波波形上均匀分布。实际上这种理想条件很难实现，只是近似成立，因为采样时钟频率、正弦波频率本身也有功率谱密度分布，并不是固定在一个频率值上。
对ADC动态性能测试而言，相干采样条件如式(2)，fs是采样频率，fin是待采样正弦波频率，M是采样周期数，NFFT是采样点数。相干采样条件要求M和NFFT为整数，且互为素数，并且NFFT为2的整数次幂，可以将该条件等价为：NFFT为2的整数次幂，M为奇数或素数。
fs×M=fin×NFFT (2) 从相干采样的角度分析TDC的码密度校准信号产生，借鉴ADC动态性能测试中的相干采样，研究TDC主时钟和校准信号的相干采样问题。对TDC码密度校准而言，可以根据要求对相干采样公式进行优化，如式(3)所示，fTDC为TDC的主时钟频率，fcal为校准信号频率，M, Ncal为整数且互为素数，Ncal不要求是2的整数次幂，NFFT为2的整数次幂是傅里叶分析的要求，Ncal无此项要求。在满足相干采样且校准次数足够多的情况下，可以保证校准信号均匀分布在TDC的延迟链上。
fTDC/fcal=Ncal/M (3) 如果式(3)的fTDC, fcal两者的频率值非常接近，M, Ncal非常接近，Ncal/M的值接近于1。以fTDC作为基准，此处研究fTDC稍大于fcal的情况，fTDC–Δf = fcal, TTDC+Δt = Tcal, Δf, Δt都很小，在频域上表现为频率差值Δf，在时域上表现为时间间隔Δt，以fTDC作为基准计算得到Δt如式(4)所示，fTDC稍小于fcal的情况同上述分析。
Δt=Tcal−TTDC=1/fcal−1/fTDC=1/(fTDC−Δf)−1/fTDC=Δf/[fTDC×(fTDC−Δf)] (4) 当fcal, fTDC值相差比较小时，以上时间差可近似为Δ f/(fTDC × fTDC)；当fTDC值为200 MHz时，对应TTDC值为5 ns，如果要求TDC延迟链等效每隔10 ps就校准一次，那么对应的Tcal值为5.010 ns，求出对应的fcal值约为199.6 MHz。实际上，并非每个TDC主时钟周期都完成一次校准。假设每5个TDC主时钟周期完成一次校准(其它要求不变)，那么，对应的Tcal值为5.002 ns，求出对应的fcal值约为199.92 MHz时，经过5个TDC主时钟周期，两者相差10 ps。在FPGA上容易实现以上的频率值，fTDC可以直接由外部时钟源直接提供，上述计算得到的fcal频率值可以利用FPGA内部的混合模式时钟管理模块(Mixed-Mode Clock Management, MMCM)资源产生，这种情况下，fTDC和fcal采用同一个时钟源，经过FPGA内部的MMCM产生校准信号，FPGA内部的MMCM资源输出附加的时钟抖动一般100 ps左右，单次校准会增加TDC的时间误差，同第2节描述，多次校准可以把这种时间误差平均化，最终实现对TDC延迟链的校准。
另外一种情况是直接采用两个标称频率值相同的时钟源，分别作为fTDC和fcal的时钟源，理论上两个时钟源的功率谱密度分布不完全相同，两个时钟源不可能输出完全相同频率值，两者之间有很小的频率差，可以认为是相干采样。前文已述，经过MMCM之后的输出会加入额外的时钟抖动，因此可以把时钟信号从专用引脚输入，直接作为TDC的主时钟、校准信号，可以降低传播链路上的抖动。
在码密度校准时，如果校准信号频率过高且直接进入到延迟链中，可能会造成TDC输出编码错误，这就需要对校准信号进行输出保持，以达到以下目的：(1)确保校准过程中TDC的输出编码的有效性；(2)定义经过输出保持后的信号为随机信号，认为随机信号和TDC主时钟无关。一种典型的输出保持电路结构如图3所示，D触发器输入端置‘1’，把校准信号作为D触发器的时钟信号，校准信号的上升沿开始一次随机过程，一次测量结束后对D触发器进行复位清零，等待校准信号的下一个上升沿再次输出高电平。由于校准信号与TDC主时钟满足相干采样条件，又经过了一级输出保持电路，输出的随机信号满足码密度校准要求，可以根据式(1)计算校准误差最大值。
4. 实现及测试
在Xilinx公司28 nm工艺的Kintex-7 FPGA上，采用级联进位链的方法设计实现plain TDC，共使用进位链资源128个，抽头数量256个，精细时间测量范围大于5 ns。论文设计的校准电路结构如图4所示。校准电路模块主要由校准信号产生及保持部分、校准控制部分构成，校准输出的二进制编码结果进入微分统计表、积分查找表(建表)等。校准信号经过保持电路之后认为是随机信号，其产生及保持受校准控制部分控制，随机信号进入到由级联进位链构成的TDC中，精细时间测量结果通过二进制编码输出到建表部分；校准控制起到控制校准使能、控制校准次数、控制建表查询输出等作用；把每次获得的校准结果编码送入微分统计表，根据微分统计表的结果建立积分查找表。在TDC测试时，输出对应的二进制编码至后端分析得到具体的时间信息。
基于相干采样理论，采用两个独立时钟源分别作为fTDC和fcal的时钟源，从专用时钟引脚输入，经过MMCM之后，输出作为TDC的主时钟、校准信号，对进位链plain TDC进行码密度校准。Kintex-7上的单个进位链一般可以输出4个抽头数据，分别是CO0～CO3，经过码密度校准，典型的4抽头的码宽如图5(a)所示，可见抽头码宽并不均匀，与文献[4]中90 nm工艺的Virtex-4 FPGA的进位链抽头码宽类似，Virtex-4进位链抽头码宽示意图如图5(b)所示。对比两者，可见制造工艺的改进的确降低了进位链抽头码宽，但是，对进位链抽头码宽的不均匀性改善不大。
结合文献[7-9]的建议，从一个进位链引出两个抽头，将其分割为2个基本延时单元，分别是 “CO0+CO3”和“CO1+CO3” 两种抽头方式，对应简写为“0tap+3tap”和“1tap+3tap”，研究了两种抽头方式对TDC分辨率和非线性的影响，结果如图6所示，采用“CO0+CO3”的2抽头方式，可以在TDC的分辨率和非线性之间取得较好的均衡。图6显示，每间隔100个码址会出现一个超宽码，这是因为一个时钟区域内只有50个上下级联的进位链，每个进位链引出2个抽头，共100个抽头，之后进位链就需要跨时钟域，不同时钟域会导致超宽码的产生。本文进位链抽头起始位置并不是时钟区域的最底部，所以超宽码出现在94, 95, 193, 194抽头处。
在“0tap+3tap”抽头方式下，利用文中所述方法，校准得到TDC的抽头数量和延迟时间的值，经过线性拟合之后的结果如图7所示，时间分辨率为24.9 ps，对应plain TDC输出二进制编码的最低有效位(Least Significant Bit, LSB)，图7显示的TDC的时间线性度较好，拟合优度为0.9997。图8(a)给出了校准得到的TDC的微分非线性(Differential Non-Linearity, DNL)指标，在“0tap+3tap”抽头方式下，DNL范围(–0.84～3.1)LSB，DNL图中的突出部分对应的抽头位置同图6一致。图8(b)给出了校准得到的TDC的积分非线性(Integral Non-Linearity, INL)指标，在“0tap+3tap”抽头方式下，INL范围(–5.2～2.2)LSB。经过对INL分析得到，在同一个时钟区域内自下向上级联的进位链，越向上，进位链抽头对应的延迟时间值越小，对应到图8(a)，抽头位置从0到93，INL是一个缓慢下降的过程，抽头位置从94到193，INL亦如是。对比参考文献[1, 2, 4, 10]中的TDC码宽合非线性参数典型测试结果，本文所述校准方法得到的结果与之符合较好，证明该方法可行。
为了验证基于相干采样的码密度校准结果的稳定性和可重复性，多次校准记录同一个抽头的延时，反复测量36次(校准次数N=36)，其分布如图9所示，分别显示了i为92, 94, 96, 98时，共4个码宽及其标准差，i表示抽头位置，ti表示第i个抽头码宽，σi表示第i个抽头标准差，其中抽头94是跨时钟域产生的。可以看到，4个抽头的码宽随时间发生变化，纵轴时间变化范围2 ps，测量36次，同一个抽头码宽的一致性比较好，σi优于0.5 ps，根据前述式(1)，已知文中所用校准方法的校准误差最大值στ为5 ps(T=5 ns, N=1000000), σi远小于5 ps。
5. 结论
基于相干采样理论，本文提出并验证了一种通用的TDC码密度校准信号产生方法，确保TDC主时钟和校准信号的频率相干，结合输出保持电路，保证校准用的随机信号在TDC延迟路径上的均匀分布，实现了对TDC的bin-by-bin校准。采用Kintex-7 FPGA内部的进位链实现plain TDC，并利用所述的方法校准plain TDC的码宽，研究测试了2抽头方式下的TDC性能参数，在“CO0+CO3”的抽头方式下，时间分辨率(对应LSB)为24.9 ps，微分非线性为(–0.84～3.1)LSB，积分非线性为(–5.0～2.2)LSB，该测试方法得到的结果和经典文献[1,2,4,10]给出的测试结果符合较好。多次测试考核结果表明：文中所述方法采用的时钟逻辑，单个延时单元的标准差优于0.5 ps。对比两种经典的基于组合逻辑电路的码密度校准信号产生方法，本文基于相干采样理论，提出了利用时钟逻辑资源产生校准信号的方法，校准结果的稳定性和重复性好。本文提出的通用码密度测量方法同样适用于其他类型的TDC的码密度校准。
-
[1] 周浩. 基于FPGA进位链的时间数字转换器设计[D]. [硕士论文], 重庆邮电大学, 2017.ZHOU Hao. Design of a time-to-digital converter based on carry-in lines of FPGA[D]. [Master dissertation], Chongqing University of Posts and Telecommunications, 2017. [2] 范欢欢. 基于FPGA的时间数字转换电路的若干关键技术的研究[D]. [博士论文], 中国科学技术大学, 2015.FAN Huanhuan. Some key technologies about time-to-digital converter based on FPGA[D]. [Ph. D. dissertation], University of Science and Technology of China, 2015. [3] WU Jinyuan. Several key issues on implementing delay line based TDCs using FPGAs[J]. IEEE Transactions on Nuclear Science, 2010, 57(3): 1543–1548. doi: 10.1109/TNS.2010.2045901 [4] BAYER E and TRAXLER M. A high-resolution (< 10 ps RMS)48-channel time-to-digital converter (TDC) implemented in a field programmable gate array (FPGA)[J]. IEEE Transactions on Nuclear Science, 2011, 58(4): 1547–1552. doi: 10.1109/TNS.2011.2141684 [5] FISHBURN M W, MENNINGA L H, FAVI C, et al. A 19.6 ps, FPGA-based TDC with multiple channels for open source applications[J]. IEEE Transactions on Nuclear Science, 2013, 60(3): 2203–2208. doi: 10.1109/TNS.2013.2241789 [6] 高丽江, 杨海钢, 李威, 等. 具有高资源利用率特征的改进型查找表电路结构与优化方法[J]. 电子与信息学报, 2019, 41(10): 2382–2388. doi: 10.11999/JEIT190095GAO Lijiang, YANG Haigang, LI Wei, et al. A circuit optimization method of improved lookup table for Highly efficient resource utilization[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2382–2388. doi: 10.11999/JEIT190095 [7] WANG Yonggang and LIU Chong. A 3.9 ps time-interval RMS precision time-to-digital converter using a dual-sampling method in an UltraScale FPGA[J]. IEEE Transactions on Nuclear Science, 2016, 63(5): 2617–2621. doi: 10.1109/TNS.2016.2596305 [8] HU Xueye, ZHAO Lei, LIU Shubin, et al. A stepped-up tree encoder for the 10-ps wave union TDC[J]. IEEE Transactions on Nuclear Science, 2013, 60(5): 3544–3549. doi: 10.1109/TNS.2013.2265555 [9] ZHAO Lei, HU Xueye, LIU Shubin, et al. The design of a 16-channel 15 ps TDC implemented in a 65 nm FPGA[J]. IEEE Transactions on Nuclear Science, 2013, 60(5): 3532–3536. doi: 10.1109/TNS.2013.2280909 [10] 王巍, 董永孟, 李捷, 等. 基于FPGA的高精度多通道时间数字转换器设计[J]. 微电子学, 2015, 45(6): 698–701, 705.WANG Wei, DONG Yongmeng, LI Jie, et al. Design of a high resolution and multichannel TDC based on FPGA[J]. Microelectronics, 2015, 45(6): 698–701, 705. 期刊类型引用(8)
1. 项圣文，包朝伟，蒋伟，唐万韬. 基于FPGA的高精度时间数字转换器设计与实现. 电子与封装. 2025(01): 39-45 . 
百度学术2. 李海涛，渠红光，赵春滨，刘森，田耕. 数字示波器模拟输入带宽测试方法研究. 电子技术应用. 2025(01): 46-49 . 百度学术3. 白文华. 基于TDC的数字化电能计量远程校准及在线测量方法. 工业计量. 2024(05): 24-27 . 百度学术4. 许玥，谢杰，曾中明，张宝顺，吴东岷. 面向FPGA-TDL-TDC的延迟时间逐位校准网络. 电子测量与仪器学报. 2024(07): 89-96 . 百度学术5. 李国梁，韩斌，程阳，曹杰，鲍春，吴昊泽. 相控-延时链混合架构时间数字转换器. 中国测试. 2023(06): 130-136 . 百度学术6. 肖远，梁华国，汪玉传，鲁迎春，易茂祥，姚亮. 非线性优化的时间数字转换器设计. 微电子学. 2023(05): 772-778 . 百度学术7. 黄春申，周严，张晶. 基于FPGA的时间数字转换技术综述. 飞控与探测. 2023(06): 51-62 . 百度学术8. 李海涛，李斌康，田耕，阮林波，吕宗璟. 一种进位链TDC的实现及其抽头方式研究. 电子技术应用. 2022(04): 53-56+61 . 百度学术其他类型引用(5)
-
下载:
下载:
百度学术
计量
- 文章访问数: 1447
- HTML全文浏览量: 805
- PDF下载量: 204
- 被引次数: 13
下载:
