基于人工神经网络的复杂介质中波的传播不确定性分析方法

程曦; 张志勇

doi:10.11999/JEIT200755

基于人工神经网络的复杂介质中波的传播不确定性分析方法

doi: 10.11999/JEIT200755

程曦,
张志勇^,

新疆农业大学计算机与信息工程学院乌鲁木齐 830052

基金项目: 国家自然科学基金(61701427)

详细信息

作者简介:
程曦：女，1986年生，讲师，研究方向为计算电磁学、人工神经网络

张志勇：男，1984年生，讲师，研究方向为计算电磁学、人工神经网络、农业信息化

通讯作者:
张志勇　jsjzzy@xjau.edu.cn

中图分类号: TN959; O441.4
计量
- 文章访问数: 614
- HTML全文浏览量: 384
- PDF下载量: 38
- 被引次数: 0
出版历程
- 收稿日期: 2020-08-26
- 修回日期: 2021-09-11
- 网络出版日期: 2021-10-28
- 刊出日期: 2021-12-21

An Uncertainty Analysis Method of Wave Propagation in Complex Media Based on Artificial Neural Network

Xi CHENG,
Zhiyong ZHANG^,

Institute of Computer and Information Engineering, XinJiang Agricultural University, Urumqi 830052, China

Funds: The National Natural Science Foundation of China (61701427)

摘要

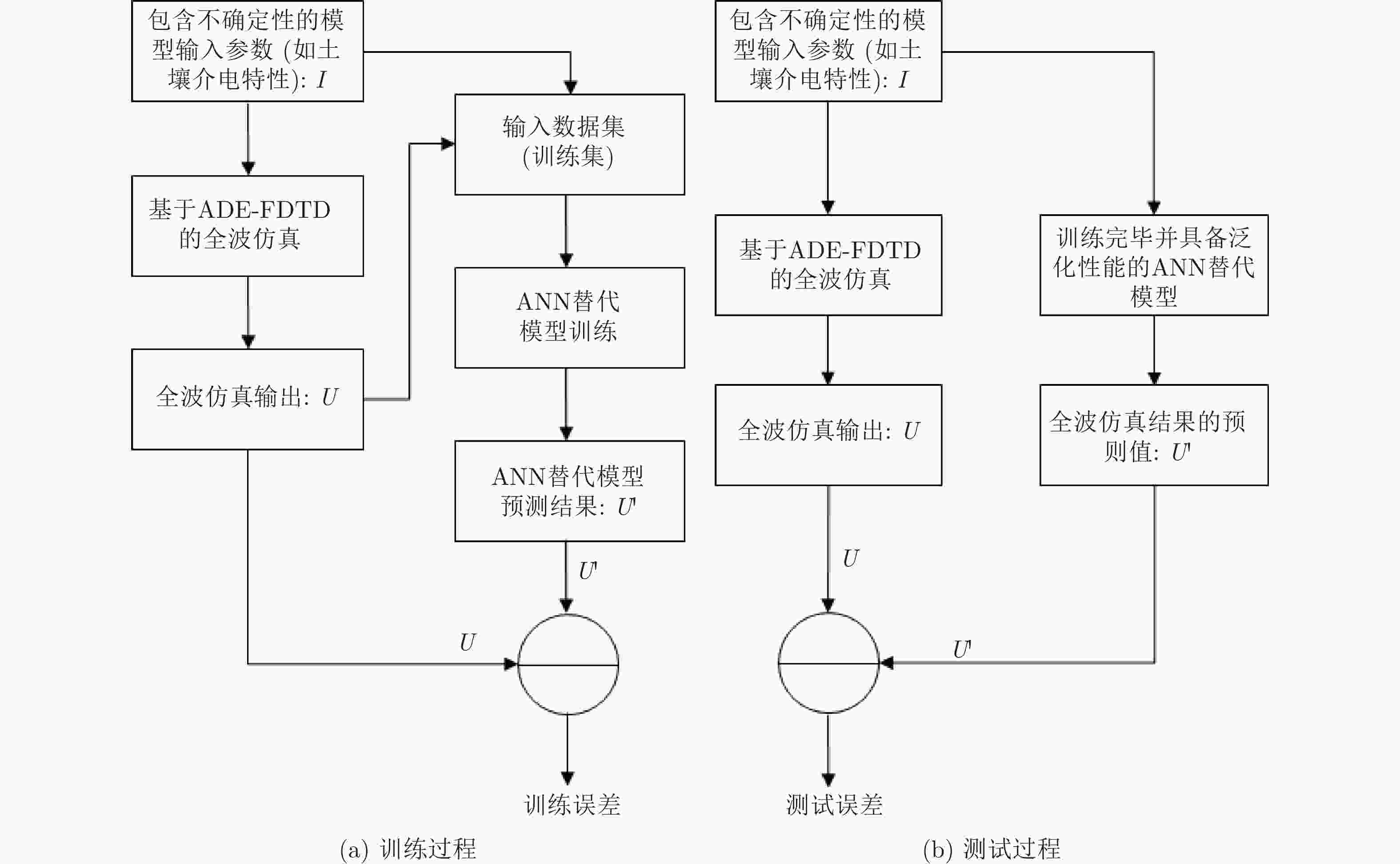
摘要: 土壤在物理系统的工作频率范围内可能表现出较强的色散性，色散物质的不确定参数在波传播的仿真结果中引入了不确定性。在考虑这些仿真结果的可接受性时，量化仿真结果中的不确定性至关重要。针对传统不确定性分析法计算效率低、运算量大的问题，该文以探地雷达建模仿真中的不确定性分析为例，提出一种基于人工神经网络的不确定性分析模型，阐述了模型的构建过程，及克服过拟合问题的策略。作为探地雷达全波仿真的替代模型能够预测仿真结果，进而得到仿真结果的统计信息，如均值、标准差。经比较，在相同的数值模型、不确定性输入参数个数，以及参数变化范围为10%的前提条件下，对任意一组输入参数，输出得到1000组结果时，该方法所得预测结果统计特性与执行全波仿真所得具有较好的一致性，且显著降低运算量，计算时间效率提升79.82%。
- 探地雷达 /
- 不确定性分析模型 /
- 人工神经网络
Abstract: Soil materials can exhibit strongly dispersive properties in the operating frequency range of a physical system, and the uncertain parameters of the dispersive materials introduce uncertainties in the simulation result of propagating waves. It is essential to quantify the uncertainty in the simulation result when the acceptability of these calculation results is considered. To avoid performing thousands of full-wave simulations, an efficient surrogate model based on ANN (Artificial Neural Network) is proposed, to imitate the concerned Ground Penetrating Radar (GPR) calculation. Meanwhile, the process of constructing the surrogate model and the strategy to overcome the overfitting problem are presented in details. As a surrogate model for full-wave simulation of ground penetrating radar, it can predict the simulation result, and then obtain the statistical information of the simulation result, such as mean value and standard deviation. After comparison, under the same conditions that the same numerical model, the number of uncertain input parameters are same, and the variation in the parameter is 10%, the statistical properties of the prediction results obtained by the proposed method are in good agreement with the results obtained by performing a thousand full-wave simulations. It also significantly reduces the amount of calculations, and the calculation time efficiency is increased by 79.82%.
- Ground Penetrating Radar (GPR) /
- Uncertainty analysis model /
- Artificial Neural Network ( ANN)

HTML全文

图 1 ANN替代模型的训练过程与测试过程

下载: 全尺寸图片幻灯片

图 2 4种不同激活数属分别应用于ANN替代模型隐藏层后训练损失函数与验证损失函数随Epochs的变化关系(未应用DropOut方法)

下载: 全尺寸图片幻灯片

图 3 探地雷达系统及其应用场景模拟模型

下载: 全尺寸图片幻灯片

图 4 基于MCS方法的电场强度$ {E_z} $变化规律

下载: 全尺寸图片幻灯片

图 5 土壤中含有金属块以及花岗岩，输入不确定性参数个数为7且变化波动范围均为10%时，$ {R_x} $处电场强度$ {E_z} $统计特性

下载: 全尺寸图片幻灯片

图 6 土壤中含有金属块以及花岗岩，输入不确定性参数个数为7且变化波动范围均为10%时，$ {R_x} $处电场强度$ {E_z} $统计特性

下载: 全尺寸图片幻灯片

图 7 土壤中含有金属块，输入不确定性参数个数为7且变化波动范围均为10%时，$ {R_x} $处电场强度$ {E_z} $统计特性

下载: 全尺寸图片幻灯片

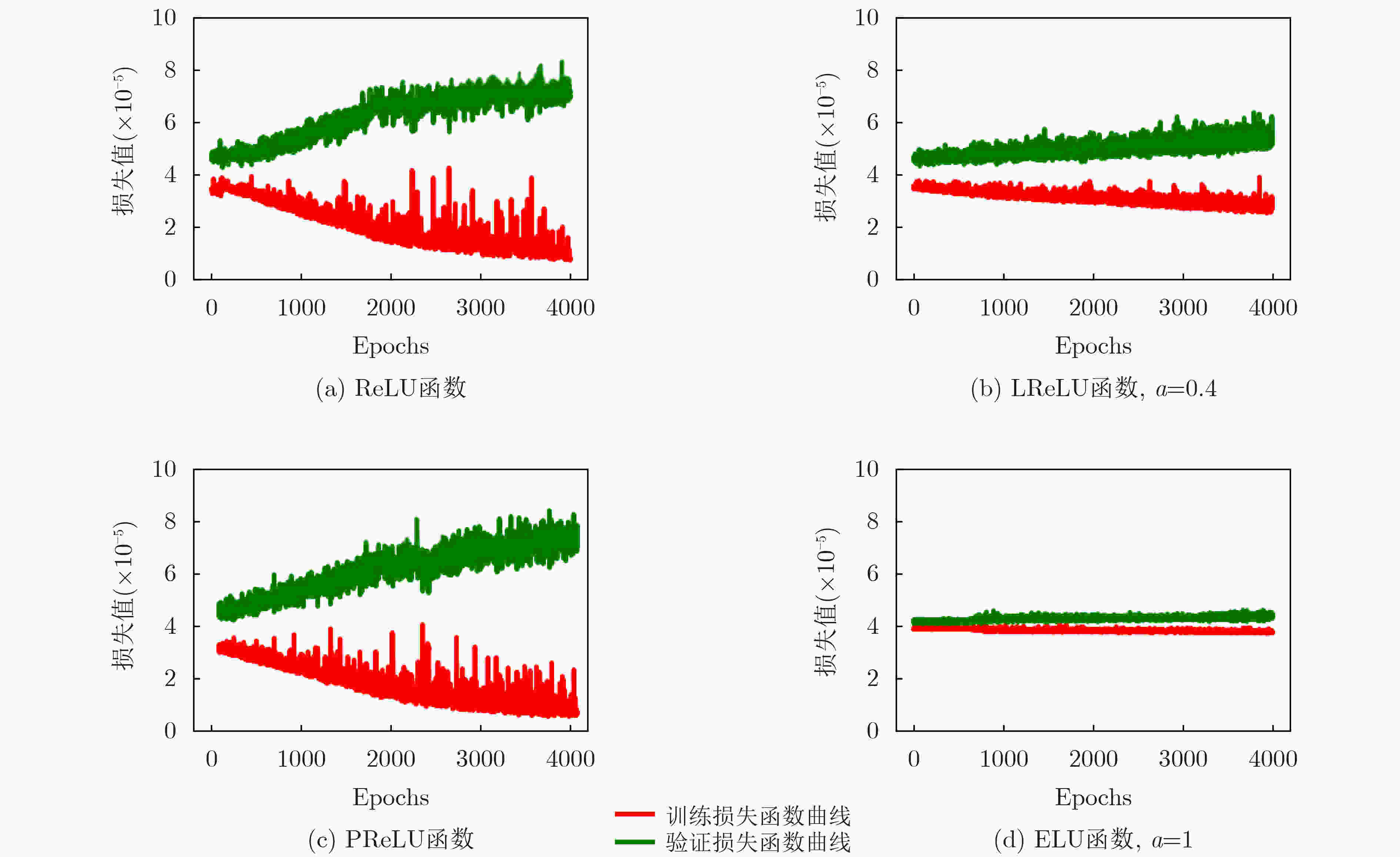
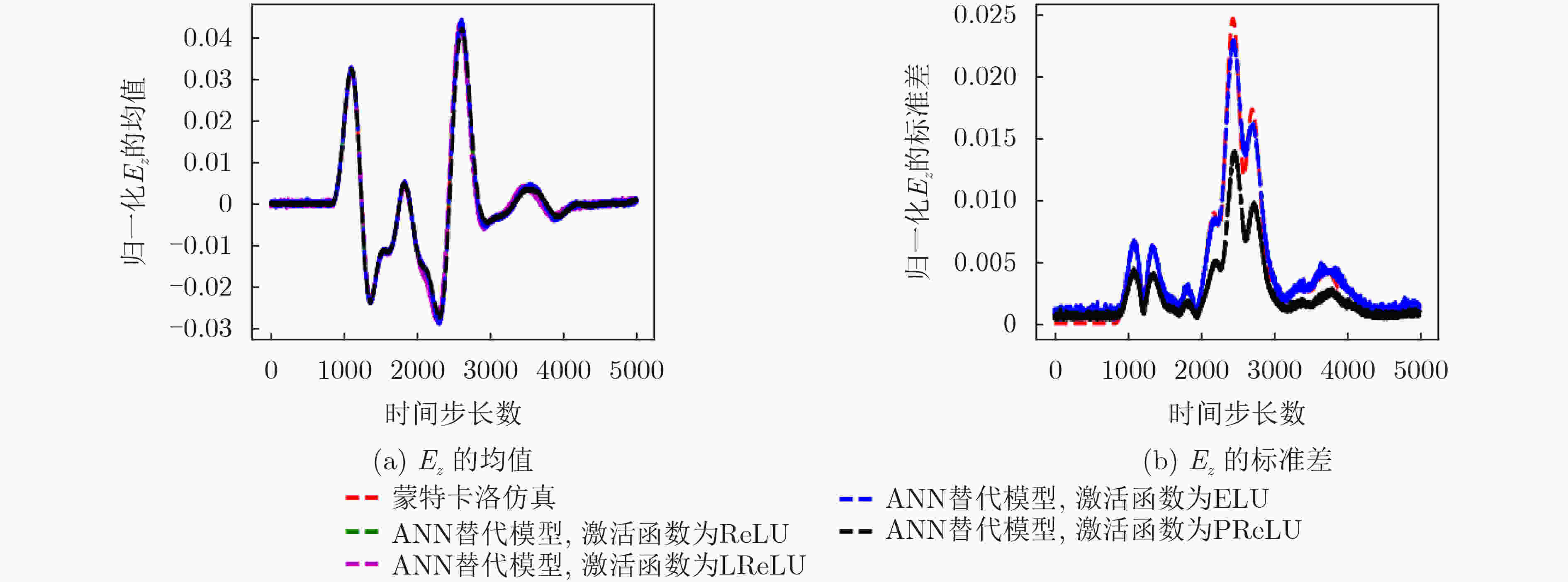
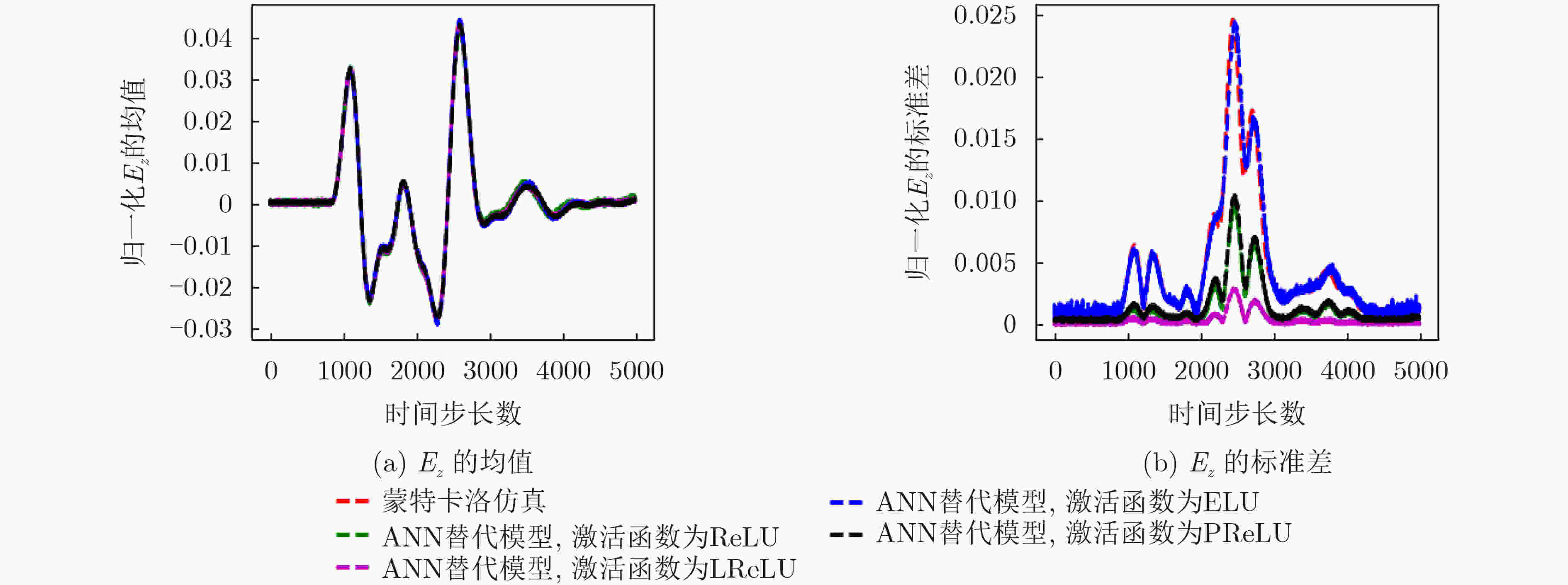
表 1 应用DropOut方法前后，不同激活函数作用时ANN替代模型的损失函数值

激活函数	网络是否应用 DropOut方法	训练数据损失 (×10^–5)	验证数据损失 (×10^–5)
ReLU函数	否	0.763	6.98
ReLU函数	是	3.730	4.28
LReLU函数	否	2.780	5.50
LReLU函数	是	3.720	4.36
PReLU函数	否	0.953	7.65
PReLU函数	是	3.730	4.30
ELU函数	否	3.740	4.30
ELU函数	是	/	/

下载: 导出CSV

表 2 色散土壤模型参数

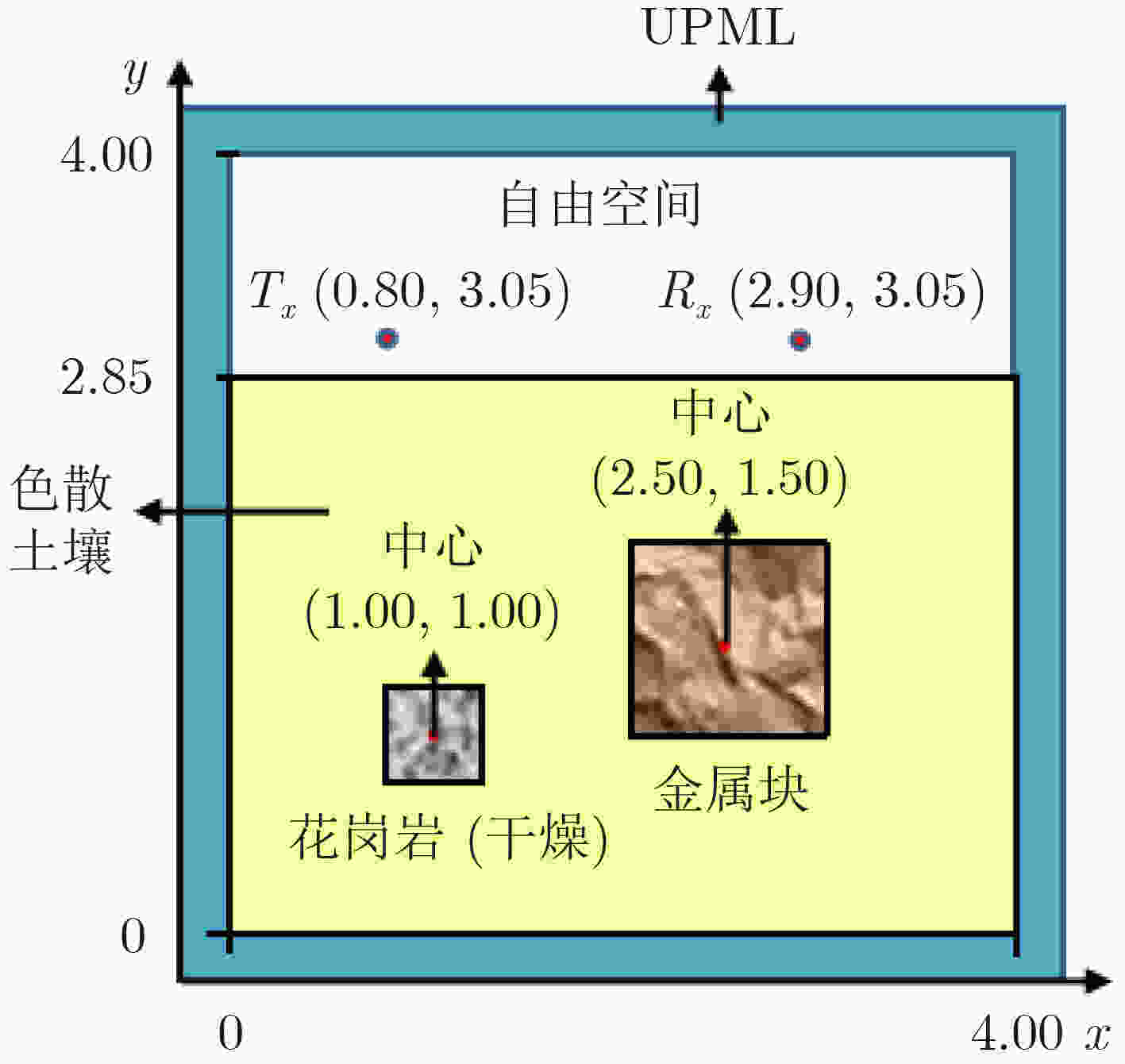
土壤湿度(%)	$ {\varepsilon _\infty } $	$ {\sigma _{\text{s}}} $（mS/m）	$ {A_1} $	$ {A_2} $	$ {\tau _1} $（ns）	$ {\tau _1} $（ns）
2.5	3.20	0.397	0.75	0.30	2.71	0.108
5	4.15	1.110	1.80	0.60	3.79	0.151
10	6.00	2.000	2.75	0.75	3.98	0.251

下载: 导出CSV

表 3 ANN替代模型超参数设置

神经网络	Batch Size	Epochs数量	隐藏层数量及各层神经元数量
ANN替代模型	25	5000	1000，1000，1000

下载: 导出CSV

表 4 传统MCS不确定分析法和ANN替代模型进行数值模拟的CPU耗时

数值模拟方法	仿真次数	CPU耗时(s)
MCS	1000	1125663.71
ANN替代模型	200	2011.21(训练耗时)+1.80(预测耗时)

下载: 导出CSV

参考文献(19)

[1]	TEIXEIRA F L, CHEW W C, STRAKA M, et al. Finite-difference time-domain simulation of ground penetrating radar on dispersive, inhomogeneous, and conductive soils[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(6): 1928–1937. doi: 10.1109/36.729364
[2]	戴世坤, 欧阳振崇, 周印明, 等. 探地雷达频率域2.5维正演[J]. 电子与信息学报, 2021, 43(1): 145–153. doi: 10.11999/JEIT190988 DAI Shikun, OUYANG Zhenchong, ZHOU Yinming, et al. Frequency domain 2.5D GPR forward modeling[J]. Journal of Electronics &Information Technology, 2021, 43(1): 145–153. doi: 10.11999/JEIT190988
[3]	侯斐斐, 施荣华, 雷文太, 等. 面向探地雷达B-scan图像的目标检测算法综述[J]. 电子与信息学报, 2020, 42(1): 191–200. doi: 10.11999/JEIT190680 HOU Feifei, SHI Ronghua, LEI Wentai, et al. A review of target detection algorithm for GPR B-scan processing[J]. Journal of Electronics &Information Technology, 2020, 42(1): 191–200. doi: 10.11999/JEIT190680
[4]	GRANDJEAN G, GOURRY J C, and BITRI A. Evaluation of GPR techniques for civil-engineering applications: Study on a test site[J]. Journal of Applied Geophysics, 2000, 45(3): 141–156. doi: 10.1016/S0926-9851(00)00021-5
[5]	GADER P D, MYSTKOWSKI M, and ZHAO Yunxin. Landmine detection with ground penetrating radar using hidden Markov models[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(6): 1231–1244. doi: 10.1109/36.927446
[6]	TAFLOVE A and HAGNESS S. Computational Electrodynamics: The Finite-Difference Time-Domain Method[M]. 2nd ed. Boston, USA: Artech House, 2000: 120–350.
[7]	SUDRET B. Uncertainty propagation and sensitivity analysis in mechanical models contributions to structural reliability and stochastic spectral methods[D]. [Ph. D. dissertation], Université Blaise Pascal, 2007: 100–300.
[8]	CHENG X, SHAO W, WANG K, et al. Uncertainty analysis in dispersive and lossy media for ground-penetrating radar modeling[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(9): 1931–1935. doi: 10.1109/LAWP.2019.2933777
[9]	MCKAY M D, BECKMAN R J, and CONOVER W J. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]. Technometrics, 1979, 21(2): 239–245. doi: 10.1080/00401706.1979.10489755
[10]	KARLIK B and OLGAC A V. Performance analysis of various activation functions in Generalized MLP architectures of neural networks[J]. International Journal of Artificial Intelligence and Expert Systems, 2011, 1(4): 111–122.
[11]	SRIVASTAVA N. Improving neural networks with dropout[D]. [Master dissertation], University of Toronto, 2013: 3–20.
[12]	KINGMA D P and BA J. Adam: A method for stochastic optimization[C]. Proceedings of the 3rd International Conference on Learning Representations, San Diego, USA, 2015.
[13]	WU Zonghan, PAN Shirui, CHEN Fengwen, et al. A comprehensive Survey on graph neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(1): 4–24. doi: 10.1109/TNNLS.2020.2978386
[14]	ZHANG Xianming, HAN Qinglong, and GE Xiaohua. An overview of neuronal state estimation of neural networks with time-varying delays[J]. Information Sciences, 2019, 478: 83–99. doi: 10.1016/j.ins.2018.11.001
[15]	TANAKA G, NAKANE R, TAKEUCHI T, et al. Spatially arranged sparse recurrent neural networks for energy efficient associative memory[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(1): 24–38. doi: 10.1109/TNNLS.2019.2899344
[16]	ZHOU Xiaomin, LI Chen, RAHAMAN M M, et al. A comprehensive review for breast histopathology image analysis using classical and deep neural networks[J]. IEEE Access, 2020, 8: 90931–90956. doi: 10.1109/ACCESS.2020.2993788
[17]	梁振清, 陈生. 基于深度学习和雷达观测的华南短临预报精度评估[J]. 气象研究与应用, 2020, 41(1): 41–47. doi: 10.19849/j.cnki.CN45-1356/P.2020.1.09 LIANG Zhenqing and CHEN Sheng. Accuracy evaluation of nowcasting in South China based on deep learning and radar observation[J]. Journal of Meteorological Research and Application, 2020, 41(1): 41–47. doi: 10.19849/j.cnki.CN45-1356/P.2020.1.09
[18]	SMITHA N and SINGH V. Target detection using supervised machine learning algorithms for GPR data[J]. Sensing and Imaging, 2020, 21(1): 11. doi: 10.1007/s11220-020-0273-8
[19]	KANG M S, KIM N, LEE J J, et al. Deep learning-based automated underground cavity detection using three-dimensional ground penetrating radar[J]. Structural Health Monitoring, 2020, 19(1): 173–185. doi: 10.1177/1475921719838081