LFM Radar Jamming Technology Based on Non-integer Order SSC Blind Frequency Shift
-
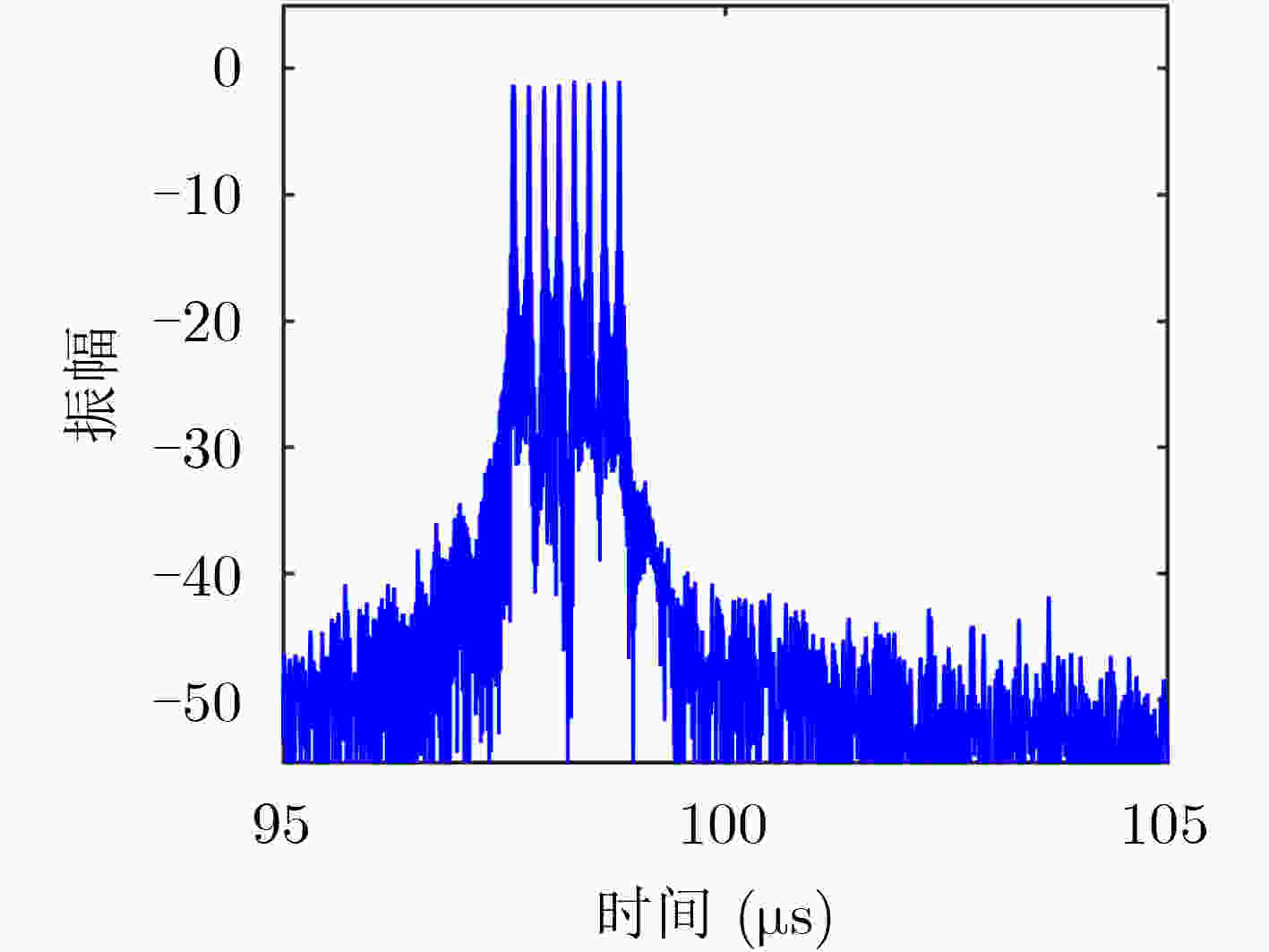
摘要: 传统频谱扩展与压缩(SSC)盲移频干扰的阶数为整数,为了实现精确的位置干扰,需要调整不同的处理延时,在实际应用中存在一定的局限性。该文对整数阶盲移频技术进行了改进,提出了一种基于非整数阶SSC盲移频的LFM雷达干扰技术。该技术在干扰机处理延时不变的情况下,通过改变SSC盲移频的阶数来实现精确的位置干扰。该文推导了一种高效的非整数阶SSC盲移频干扰实现方法,同时通过Newman序列控制信号的初相来减小压制干扰信号的峰均比(PAPR)。仿真结果表明,该文算法在指定干扰机处理延时的情况下,可以实现假目标欺骗干扰和相参密集压制干扰,能够有效对抗脉冲压缩体制雷达,具有较好的工程应用价值。Abstract: The order of traditional Spectrum Spread and Compression (SSC) blind frequency shift jamming is an integer. To achieve accurate position interference, different processing delays need to be adjusted, which has certain limitations in practical application. In this paper, the integer order blind frequency shift technology is improved, and a Linear Frequency Modulation (LFM) radar jamming technology based on non-integer order SSC blind frequency shift is proposed. The jamming can be realized by changing the precise position of the radar in different situations. In this paper, an efficient implementation method of blind frequency shift jamming for non-integer order SSC is derived. Meanwhile, the initial phase of the signal is controlled by the Newman sequence to reduce the Peak-to-Average Power Ratio (PAPR) of the jamming signal. The simulation results show that the algorithm can achieve false target deception jamming and coherent dense suppression jamming under the processing delay of a specific jammer, which can effectively counter pulse compression radar, and has good engineering application value.
-
表 1 在3种不同相位情况下的PAPR值(dB)
点数 零初相 随机相位 Newman相位 8 9.14 5.94 2.54 16 11.92 6.47 2.61 32 15.19 6.33 2.65 -
[1] FENG Dejun, XU Letao, PAN Xiaoyi, et al. Jamming wideband radar using interrupted-sampling repeater[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1341–1354. doi: 10.1109/TAES.2017.2670958 [2] 刘忠, 王雪松, 刘建成, 等. 基于数字射频存储器的间歇采样重复转发干扰[J]. 兵工学报, 2008, 29(4): 405–410. doi: 10.3321/j.issn:1000-1093.2008.04.005LIU Zhong, WANG Xuesong, LIU Jiancheng, et al. Jamming technique of interrupted-sampling and periodic repeater based on digital radio frequency memory[J]. Acta Armamentarii, 2008, 29(4): 405–410. doi: 10.3321/j.issn:1000-1093.2008.04.005 [3] 刘建成, 王雪松, 刘忠, 等. 对线性调频脉压雷达的导前假目标群干扰[J]. 电子与信息学报, 2008, 30(6): 1350–1353. doi: 10.3724/SP.J.1146.2006.00458LIU Jiancheng, WANG Xuesong, LIU Zhong, et al. Preceded false target groups jamming against LFM pulse compression radars[J]. Journal of Electronics &Information Technology, 2008, 30(6): 1350–1353. doi: 10.3724/SP.J.1146.2006.00458 [4] WU Qihua, ZHAO Feng, WANG Junjie, et al. Improved ISRJ-based radar target echo cancellation using frequency shifting modulation[J]. Electronics, 2019, 8(1): 46. doi: 10.3390/electronics8010046 [5] 张养瑞, 李云杰, 李曼玲, 等. 间歇采样非均匀重复转发实现多假目标压制干扰[J]. 电子学报, 2016, 44(1): 46–53. doi: 10.3969/j.issn.0372-2112.2016.01.008ZHANG Yangrui, LI Yunjie, LI Manling, et al. Suppress jamming technique of multiple false targets on interrupted-sampling and non-uniform periodic repeater[J]. Acta Electronica Sinica, 2016, 44(1): 46–53. doi: 10.3969/j.issn.0372-2112.2016.01.008 [6] YOUSSEF A, DRIESSEN P F, GEBALI F, et al. On time compression overlap-add technique in linear frequency modulation pulse compression radar systems: Design and performance evaluation[J]. IEEE Access, 2017, 5: 27525–27537. doi: 10.1109/ACCESS.2017.2771799 [7] ZHOU Chao, LIU Feifeng, and LIU Quanhua. An adaptive transmitting scheme for interrupted sampling repeater jamming suppression[J]. Sensors, 2017, 17(11): 2480. doi: 10.3390/s17112480 [8] 张建中, 穆贺强, 文树梁, 等. 基于LFM分段脉冲压缩的抗间歇采样转发干扰方法[J]. 电子与信息学报, 2019, 41(7): 1712–1720. doi: 10.11999/JEIT180851ZHANG Jianzhong, MU Heqiang, WEN Shuliang, et al. Anti-intermittent sampling repeater jamming method based on LFM segmented pulse compression[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1712–1720. doi: 10.11999/JEIT180851 [9] 周超, 刘泉华, 胡程. 间歇采样转发式干扰的时频域辨识与抑制[J]. 雷达学报, 2019, 8(1): 100–106. doi: 10.12000/JR18080ZHOU Chao, LIU Quanhua, and HU Cheng. Time-frequency analysis techniques for recognition and suppression of interrupted sampling repeater jamming[J]. Journal of Radars, 2019, 8(1): 100–106. doi: 10.12000/JR18080 [10] 王玉军, 赵国庆, 胡曦明. 基于延迟不变的LFM雷达移频干扰方法[J]. 系统工程与电子技术, 2009, 31(8): 1861–1863. doi: 10.3321/j.issn:1001-506X.2009.08.018WANG Yujun, ZHAO Guoqing, and HU Ximing. Method of shift-frequency jamming to LFM radar based on delay invariance[J]. Systems Engineering and Electronics, 2009, 31(8): 1861–1863. doi: 10.3321/j.issn:1001-506X.2009.08.018 [11] 王玉军, 赵国庆. 对LFM雷达的N阶SSC盲移频干扰算法[J]. 电路与系统学报, 2011, 16(4): 70–74. doi: 10.3969/j.issn.1007-0249.2011.04.014WANG Yujun and ZHAO Guoqing. Blind Nth-order SSC shift-frequency jamming to LFM radar[J]. Journal of Circuits and Systems, 2011, 16(4): 70–74. doi: 10.3969/j.issn.1007-0249.2011.04.014 [12] 颜彪, 许宗泽. 降低多载波信号峰值平均功率比的新相位方案[J]. 系统工程与电子技术, 2004, 26(12): 1782–1783. doi: 10.3321/j.issn:1001-506X.2004.12.009YAN Biao and XU Zongze. New phasing scheme to reduce peak-to-average power ratio for a multicarrier signal[J]. Systems Engineering and Electronics, 2004, 26(12): 1782–1783. doi: 10.3321/j.issn:1001-506X.2004.12.009 [13] 王杰贵, 张鹏程. 对线性调频脉冲压缩雷达的多载波调制转发干扰[J]. 电子与信息学报, 2015, 37(11): 2727–2734. doi: 10.11999/JEIT150193WANG Jiegui and ZHANG Pengcheng. Multi-carrier modulation repeater jamming against linear frequency modulated pulse-compression radar[J]. Journal of Electronics &Information Technology, 2015, 37(11): 2727–2734. doi: 10.11999/JEIT150193 [14] JAWHAR Y A, AUDAH L, TAHER M A, et al. A review of partial transmit sequence for PAPR reduction in the OFDM Systems[J]. IEEE Access, 2019, 7: 18021–18041. doi: 10.1109/ACCESS.2019.2894527 [15] VARAHRAM P, AL-AZZO W F, and ALI B M. A low complexity partial transmit sequence scheme by use of dummy signals for PAPR reduction in OFDM Systems[J]. IEEE Transactions on Consumer Electronics, 2010, 56(4): 2416–2420. doi: 10.1109/TCE.2010.5681122 [16] 刘璐, 赵国庆. 一种峰均比抑制方法的研究[J]. 电子学报, 2018, 46(10): 2443–2449. doi: 10.3969/j.issn.0372-2112.2018.10.018LIU Lu and ZHAO Guoqing. A method on peak-to-average power ratio reduction[J]. Acta Electronica Sinica, 2018, 46(10): 2443–2449. doi: 10.3969/j.issn.0372-2112.2018.10.018 -






 下载:
下载:

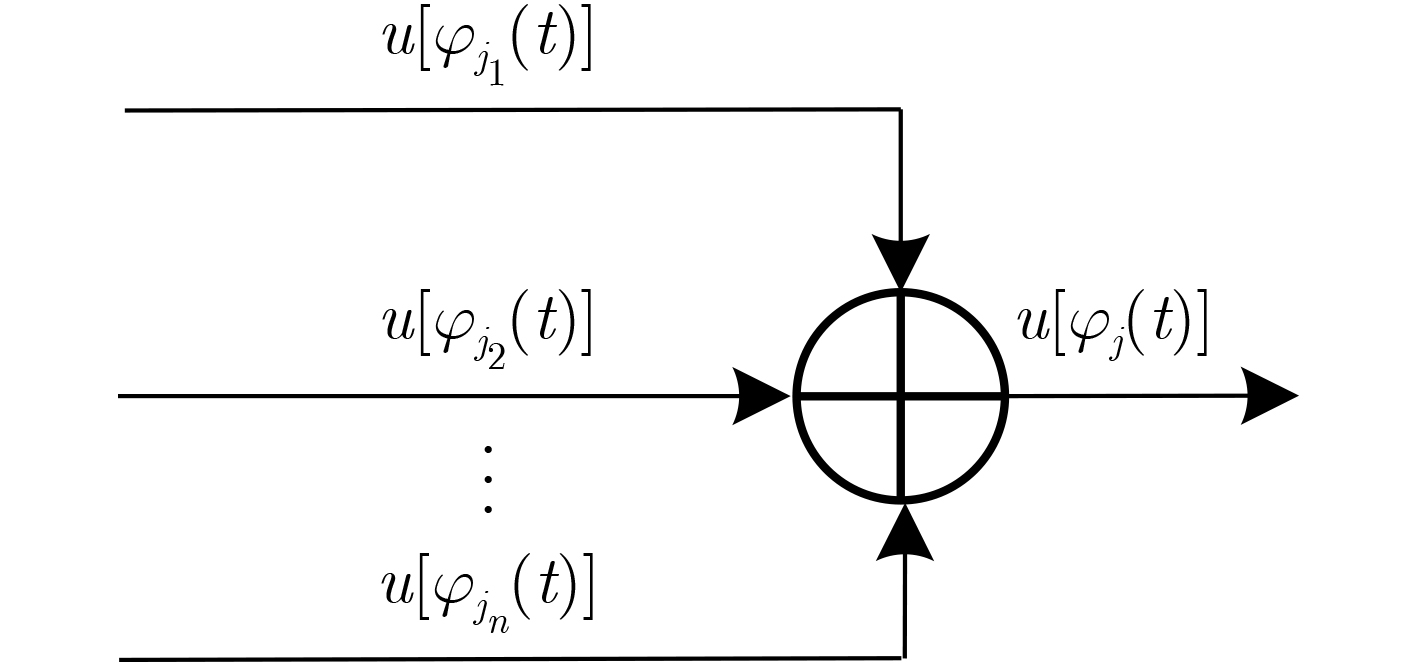
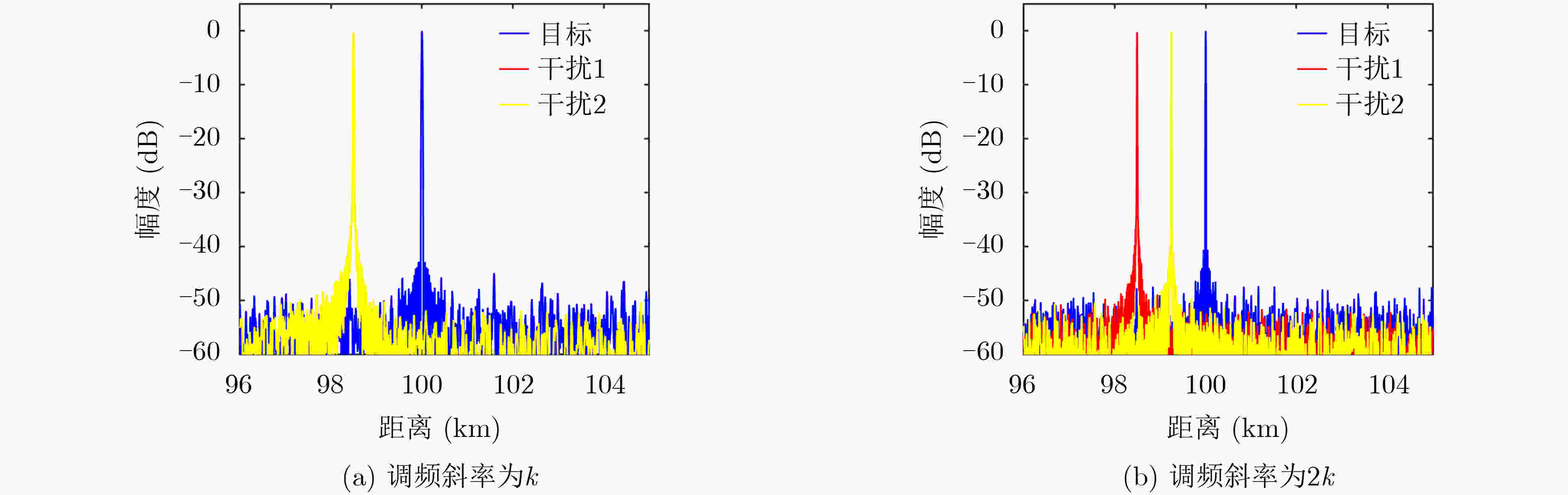
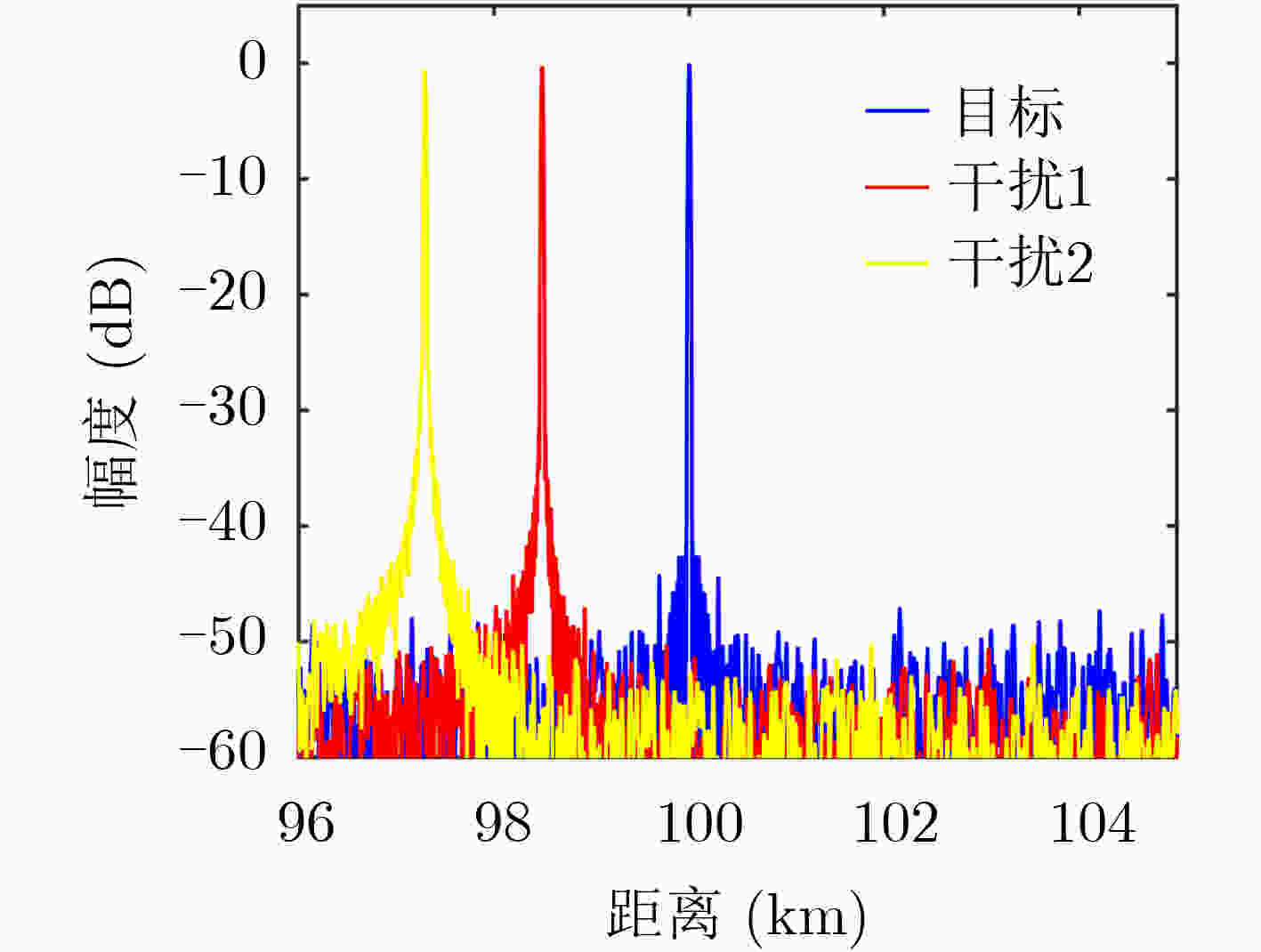
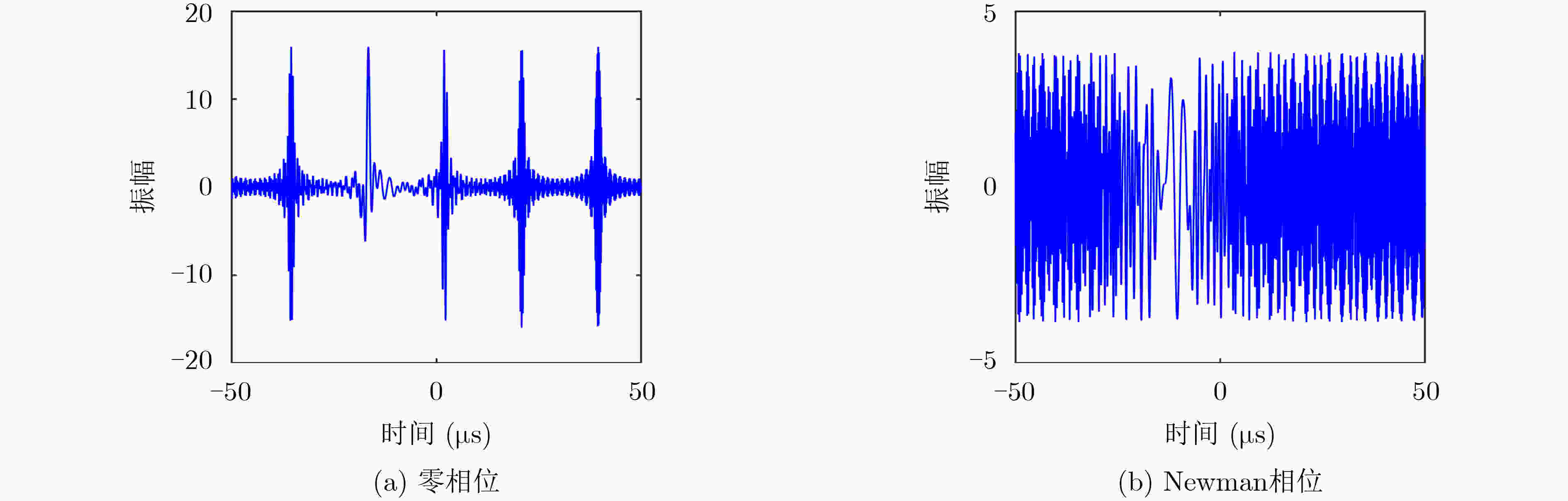


 下载:
下载:
