A Lightweight Enhanced Long Range Physical Layer Design Method for Internet of Things
-
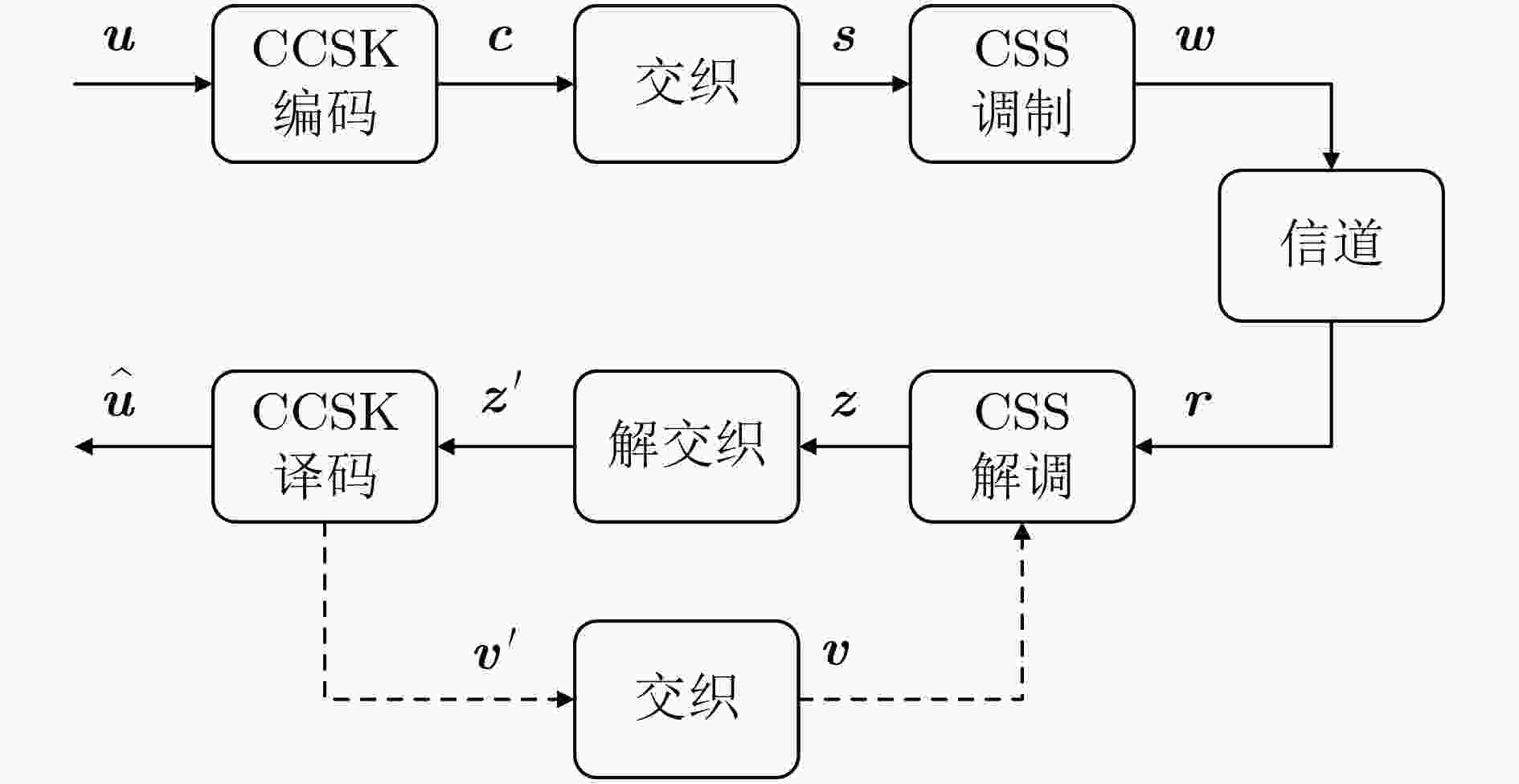
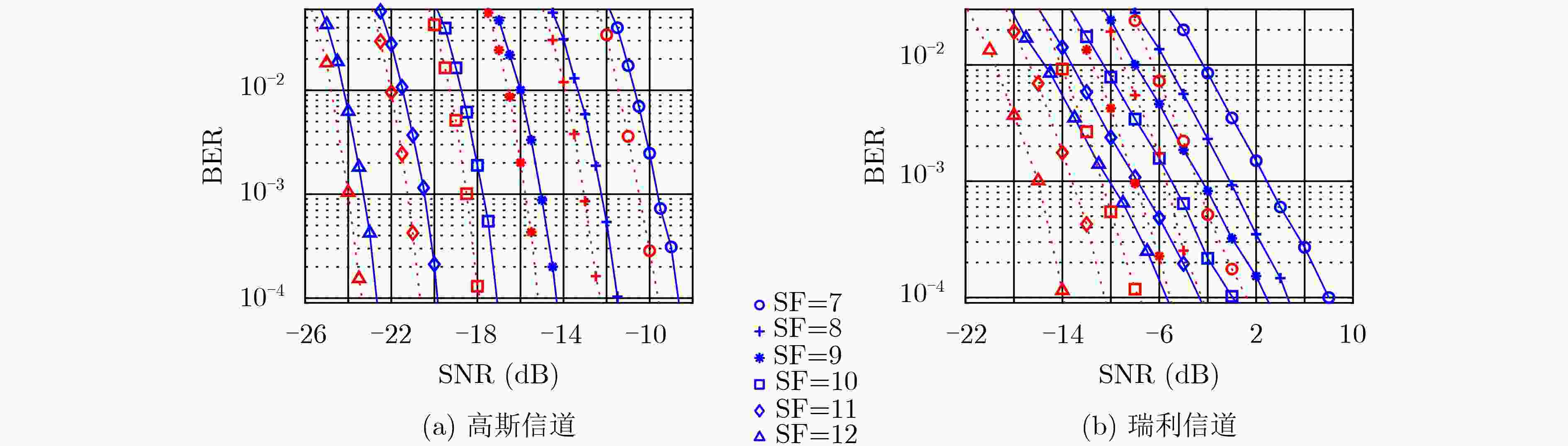
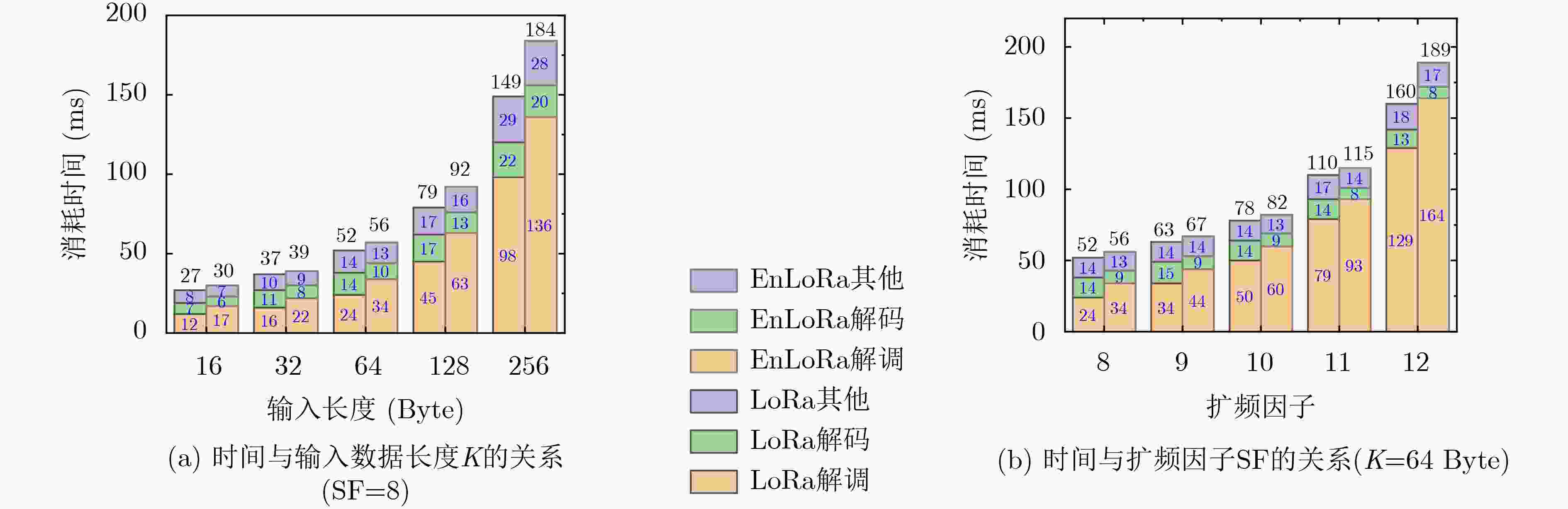
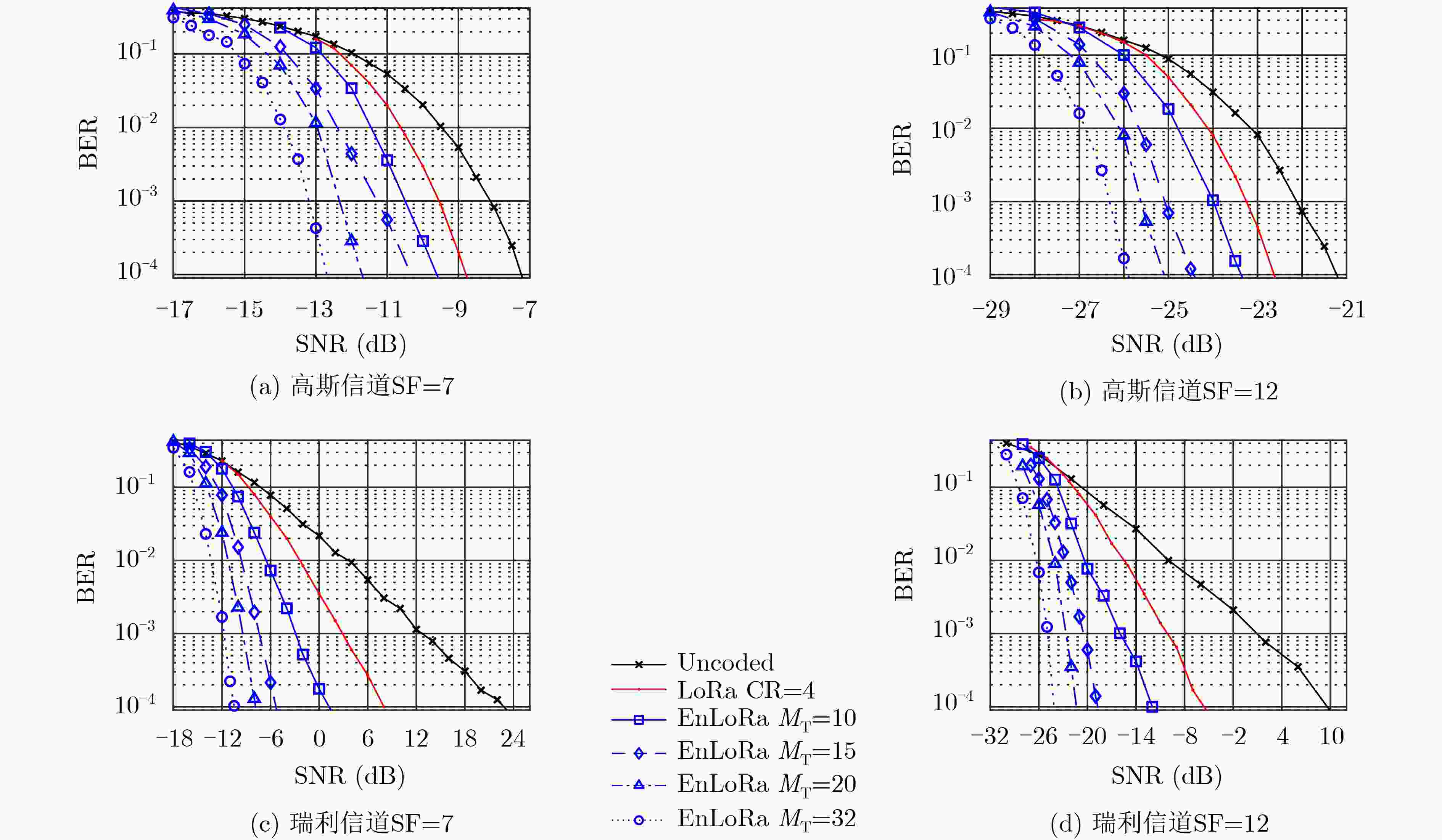
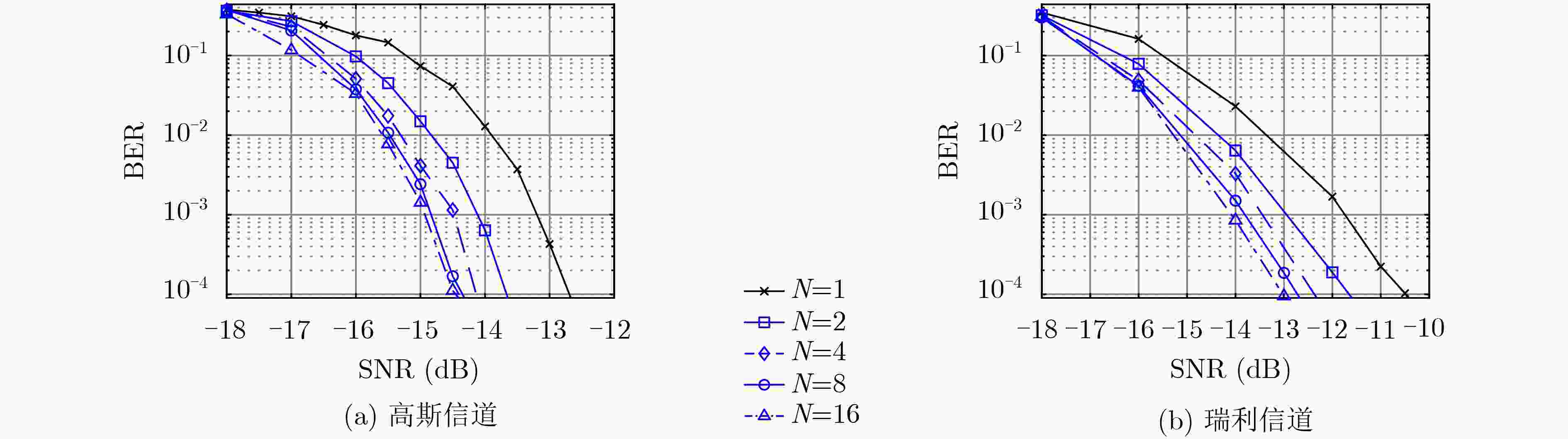
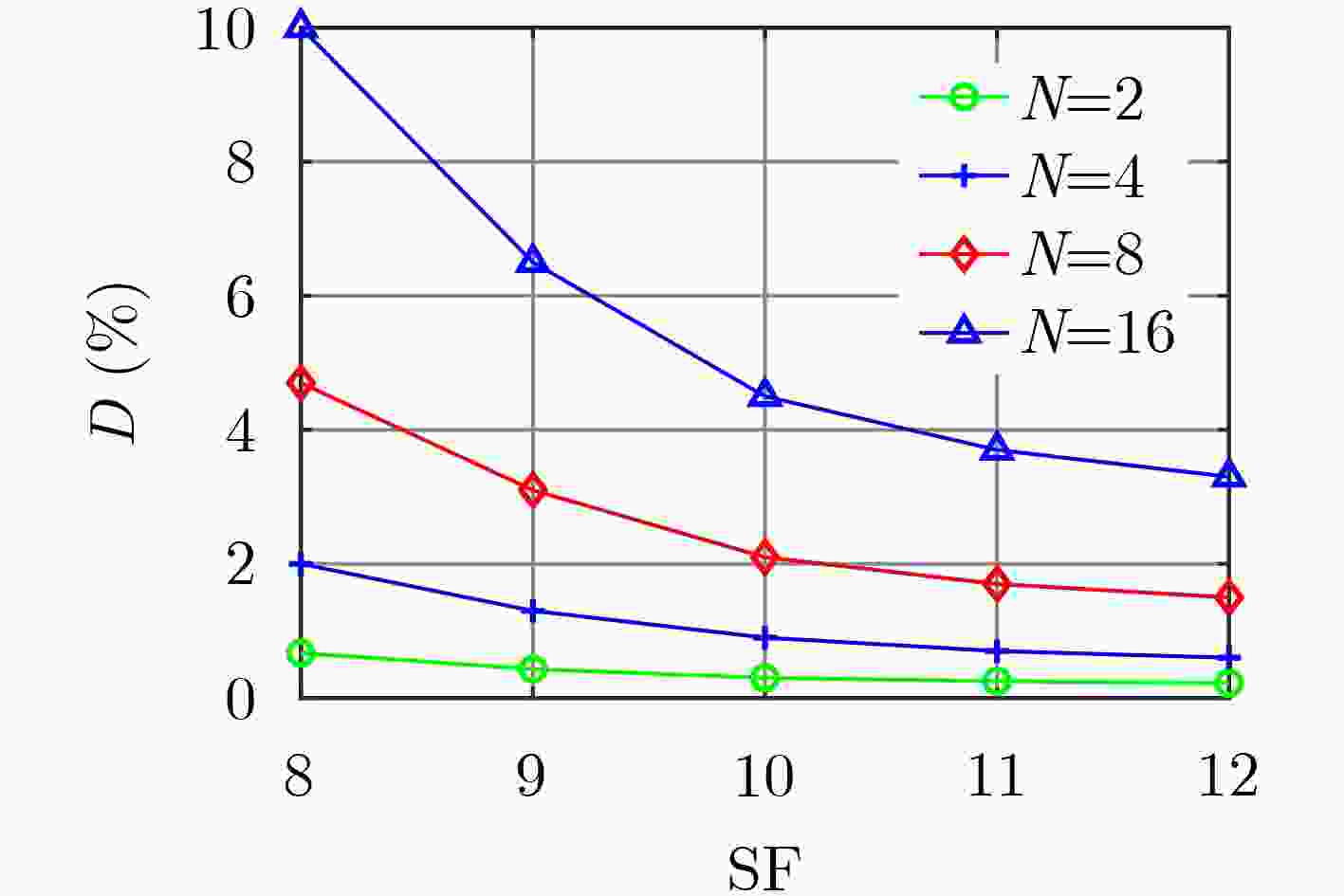
摘要: 为了提高LoRa在衰落信道下的误码率性能,该文设计了一种轻量级的增强型长距离(EnLoRa)物理层。首先,采用循环码移位键控(CCSK)作为纠错码,级联对角矩阵交织和啁啾扩频(CSS)调制技术,构造了一种新的比特交织编码调制(BICM)结构。然后,基于该结构,提出了一种基于比特对数似然比信息的软CSS解调和软译码算法,并将译码输出后的外信息作为先验信息反馈至解调模块,进行迭代译码。仿真结果表明,与相同码率的LoRa系统对比,EnLoRa系统在高斯信道下的编码增益提高了0.8 dB,在瑞利信道下的编码增益提高了7 dB。在此基础之上,通过多次迭代译码,还可以获得最大2.5 dB的额外收益。时间复杂度增加不到10%,空间复杂度增幅可忽略不计。该方法可望进一步降低物联网节点的功耗,在室内、市区和工业等复杂多径场景具有较大的应用价值。Abstract: To improve the bit error rate performance of LoRa (Long Range) in fading channels, a lightweight Enhanced Long Range (EnLoRa) physical layer is designed. First, Cyclic Code Shift Keying (CCSK) is chosen as the error correction code, and the diagonal matrix interleaving and Chirp Spread Spectrum (CSS) modulation techniques are concatenated to construct a new Bit Interleaved Coded Modulation (BICM) structure. Then, based on this structure, a soft CSS demodulation and soft decoding algorithm based on bit log-likelihood ratio information is proposed. Further, the decoded external information is fed back to the demodulation module as a priori information for iteration decoding. The simulation results show that, compared with the LoRa system of the same code rate, the coding gain of the EnLoRa system under the Gaussian channel is increased by 0.8 dB, and the coding gain under the Rayleigh channel is increased by 7 dB. On this basis, through multiple iterations, an additional gain of up to 2.5 dB can be obtained. The time complexity is only increased by 10%, and the increase in space complexity is negligible. This method is expected to reduce further the power consumption of LoRa nodes and has great application value to complex multipath scenarios such as indoors, urban areas and industries.
-
表 1 LoRa和EnLoRa系统的空间复杂度(Byte)
系统 ROM RAM LoRa ~17k ~5k EnLoRa ~22k ~9k -
[1] CENTENARO M, VANGELISTA L, ZANELLA A, et al. Long-range communications in unlicensed bands: The rising stars in the IoT and smart city scenarios[J]. IEEE Wireless Communications, 2016, 23(5): 60–67. doi: 10.1109/MWC.2016.7721743 [2] Semtech. AN1200.22: LoRa™ modulation basics[EB/OL]. https://www.docin.com/p-1913160397.html, 2015. [3] ELSHABRAWY T and ROBERT J. Closed-form approximation of LoRa modulation BER performance[J]. IEEE Communications Letters, 2018, 22(9): 1778–1781. doi: 10.1109/LCOMM.2018.2849718 [4] CATTANI M, BOANO C A, and RÖMER K. An experimental evaluation of the reliability of LoRa long-range low-power wireless communication[J]. Journal of Sensor and Actuator Networks, 2017, 6(2): 7. doi: 10.3390/jsan6020007 [5] VILLARIM M R, DE LUNA J V H, DE FARIAS MEDEIROS D, et al. An evaluation of LoRa communication range in urban and forest areas: A case study in brazil and portugal[C]. The 2019 IEEE 10th Annual Information Technology, Electronics and Mobile Communication Conference, Vancouver, Canada, 2019: 827–832. [6] SELLER O B A and SORNIN N. Low power long range transmitter[P]. USA Patent, 20140219329A1, 2014. [7] ROBYNS P, QUAX P, LAMOTTE W, et al. A multi-channel software decoder for the LoRa modulation scheme[C]. The 3rd International Conference on Internet of Things, Big Data and Security, Funchal, Portugal, 2018: 1–12. [8] MARQUET A, MONTAVONT N, and PAPADOPOULOS G Z. Towards an SDR implementation of LoRa: Reverse-engineering, demodulation strategies and assessment over Rayleigh channel[J]. Computer Communications, 2020, 153: 595–605. doi: 10.1016/j.comcom.2020.02.034 [9] MROUE H, NASSER A, PARREIN B, et al. Analytical and simulation study for LoRa modulation[C]. The 2018 25th International Conference on Telecommunications, Saint-Malo, France, 2018: 655–659. [10] ELSHABRAWY T and ROBERT J. Interleaved chirp spreading LoRa-based modulation[J]. IEEE Internet of Things Journal, 2019, 6(2): 3855–3863. doi: 10.1109/JIOT.2019.2892294 [11] BOMFIN R, CHAFII M, and FETTWEIS G. A novel modulation for IoT: PSK-LoRa[C]. The 2019 IEEE 89th Vehicular Technology Conference, Kuala Lumpur, Malaysia, 2019, 1–5. [12] ELSHABRAWY T and ROBERT T. Enhancing LoRa capacity using non-binary single parity check codes[C]. The 2018 14th International Conference on Wireless and Mobile Computing, Networking and Communications, Limassol, Cyprus, 2018: 1–7. [13] 徐浪, 陈晓莉, 田茂, 等. 基于Turbo码和ODPD判决法的LoRa改进方法[J]. 电子测量技术, 2020, 43(7): 142–147. doi: 10.19651/j.cnki.emt.1903832XU Lang, CHEN Xiaoli, TIAN Mao, et al. Improving method of LoRa based on Turbo code and ODPD[J]. Electronic Measurement Technology, 2020, 43(7): 142–147. doi: 10.19651/j.cnki.emt.1903832 [14] 朱鸿斌, 戴胜辰, 康凯, 等. 改进型极化码混合自动请求重传法[J]. 电子与信息学报, 2017, 39(5): 1136–1141. doi: 10.11999/JEIT160736ZHU Hongbin, DAI Shengchen, KANG Kai, et al. An improved HARQ scheme with polar codes[J]. Journal of Electronics &Information Technology, 2017, 39(5): 1136–1141. doi: 10.11999/JEIT160736 [15] DILLARD G M, REUTER M, ZEIDDLER J, et al. Cyclic code shift keying: A low probability of intercept communication technique[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(3): 786–798. doi: 10.1109/TAES.2003.1238736 [16] VANGELISTA L. Frequency shift chirp modulation: The LoRa modulation[J]. IEEE Signal Processing Letters, 2017, 24(12): 1818–1821. doi: 10.1109/LSP.2017.2762960 [17] VALENTI M C and CHENG Shi. Iterative demodulation and decoding of Turbo-coded M-ary noncoherent orthogonal modulation[J]. IEEE Journal on Selected Areas in Communications, 2005, 23(9): 1739–1747. doi: 10.1109/JSAC.2005.853794 [18] VITERBI A J. An intuitive justification and a simplified implementation of the MAP decoder for convolutional codes[J]. IEEE Journal on Selected Areas in Communications, 1998, 16(2): 260–264. doi: 10.1109/49.661114 -





 下载:
下载:



 下载:
下载:
