Research on Unmanned Aerial Vehicle Location Signal Separation Algorithm Based on Support Vector Machines
-
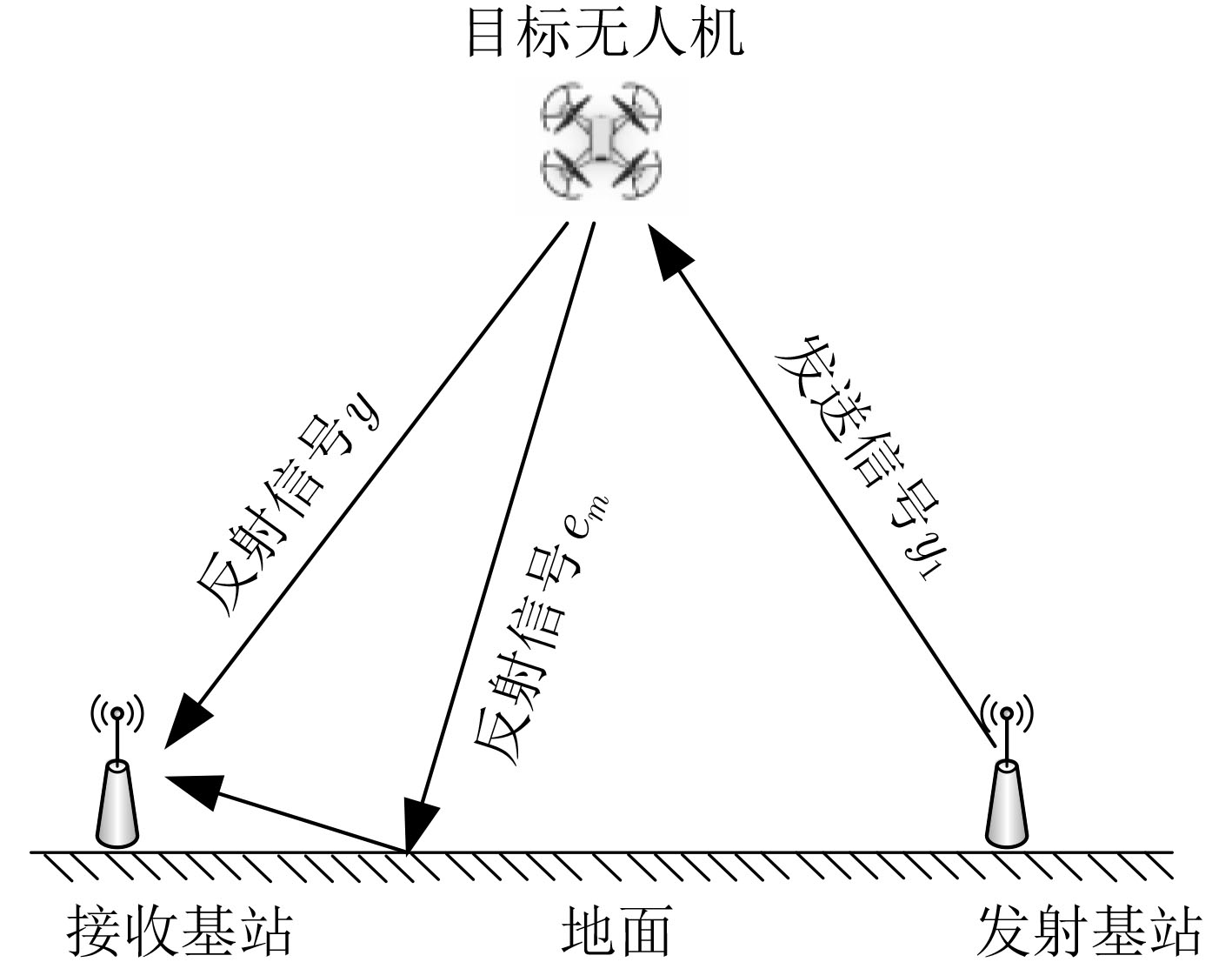
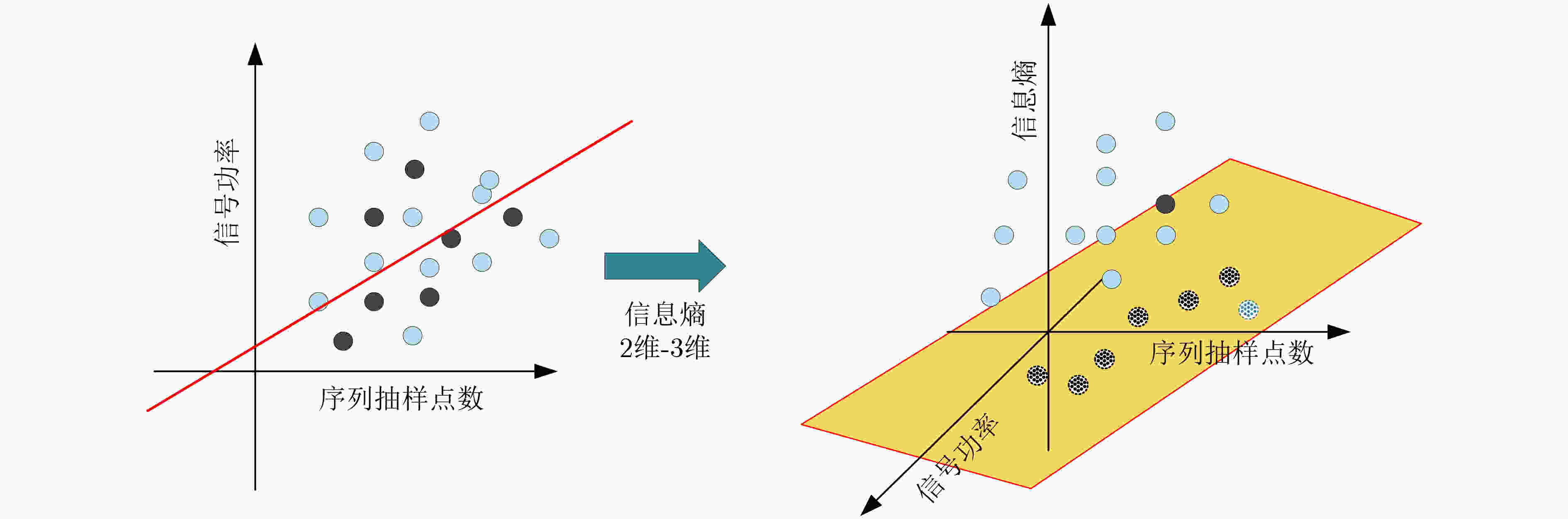
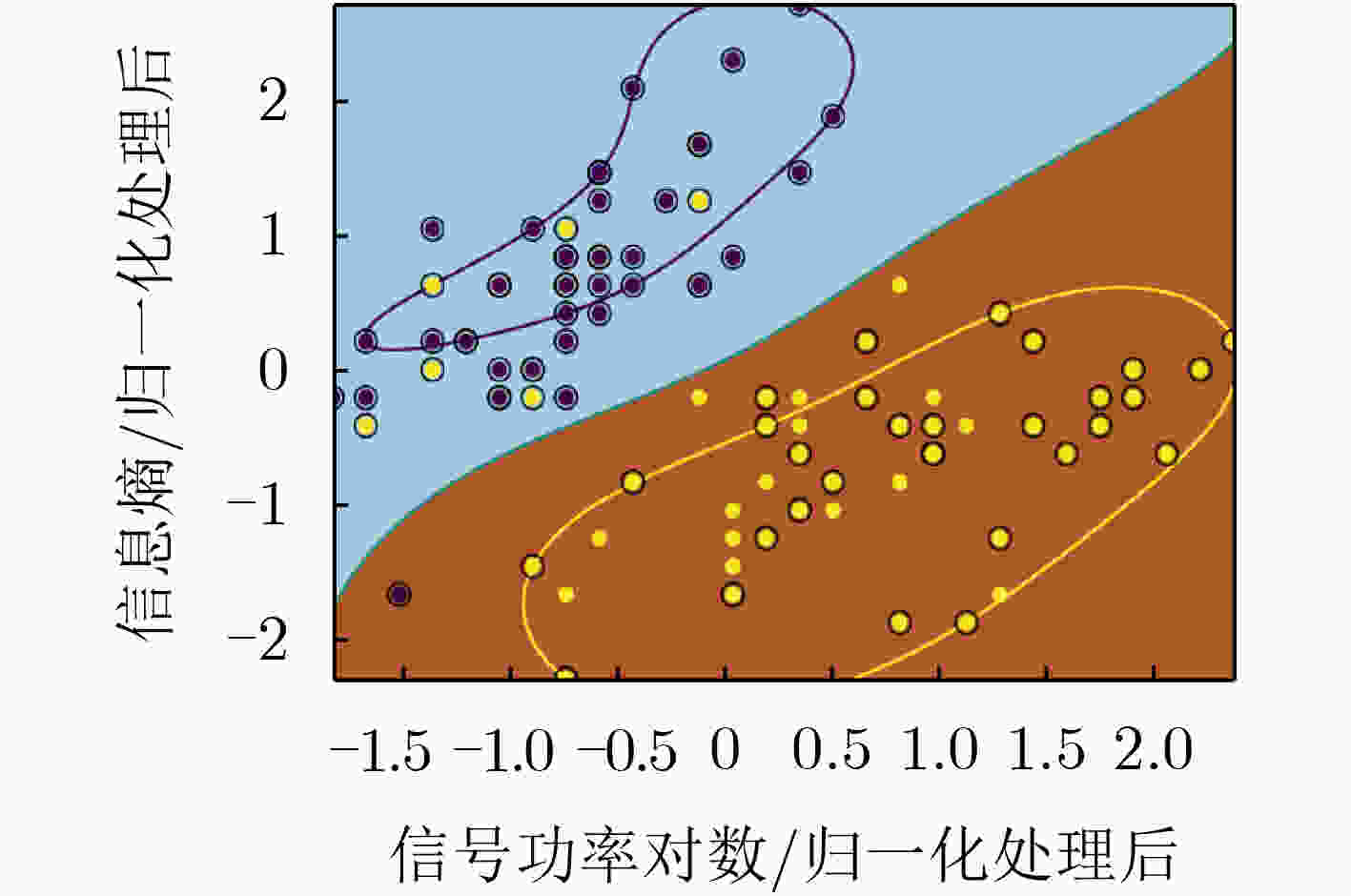
摘要: 为了解决无人机(UAV)无源定位中难以从多径干扰严重的环境中提取无人机定位信号的问题,该文提出一种基于支持向量机(SVM)的无人机定位信号分离算法,在SVM模型训练时,通过计算无人机相邻数据集之间的欧氏距离获取信息熵,为SVM映射高维空间提供模型数据。在此基础上,加入映射函数阈值软边界,使模型具有参数自适应调整能力,来适应无人机运动灵活所导致的数据差异。最后构建了观测者操作特性曲线获取无人机定位信号分离结果。仿真结果表明所提算法能够有效分离无人机定位信号与噪声,在多径干扰严重的情况下具有较高的信号分离准确率。Abstract: In order to solve the problem that it is difficult to extract the Unmanned Aerial Vehicle (UAV) positioning signal from the environment with severe multipath interference in the passive positioning of the UAV, a UAV positioning signal separation based on Support Vector Machines (SVM) algorithm is proposed. During the training of the SVM model, the information entropy is obtained by calculating the Euclidean distance between the adjacent data sets of the UAV, and the model data is provided for the SVM to map the high-dimensional space. On this basis, the soft boundary of the threshold of the mapping function is added to make the model have the ability to adjust parameters adaptively to adapt to the data difference caused by the flexible movement of the UAV. Finally, an observer operating characteristic curve is constructed to obtain the result of UAV positioning signal separation. The simulation results show that the proposed algorithm can effectively separate the UAV positioning signal and noise.
-
表 1 基于信息熵的SVM定位信息分离
输入:定位数据$\widehat{y}$,发送信号$F$,输出:目标定位信号 (1)信号抽样,并对信号进行分类,计算数据距离${d}_{i,j}$; (2)计算数据对数平均${\varphi }^{l}(r)$,重复计算$n-l$次,保证数据遍历性; (3)获取定位数据信息熵${\rm{ApEn}}(l,r)$; (4)定义SVM模型决策函数$f(T)$以及映射函数$\phi (T)$; (5)引入松弛变量${\xi }_{i}$,防止定位数据过拟合; (6)获取ROC平面以及定位数据信息熵内积函数$K({T}_{i},{T}_{j})$; (7)得到优化的映射函数$\phi ({T}_{i})$,模型建立完毕,并对目标定位信
号进行分离。表 2 仿真参数
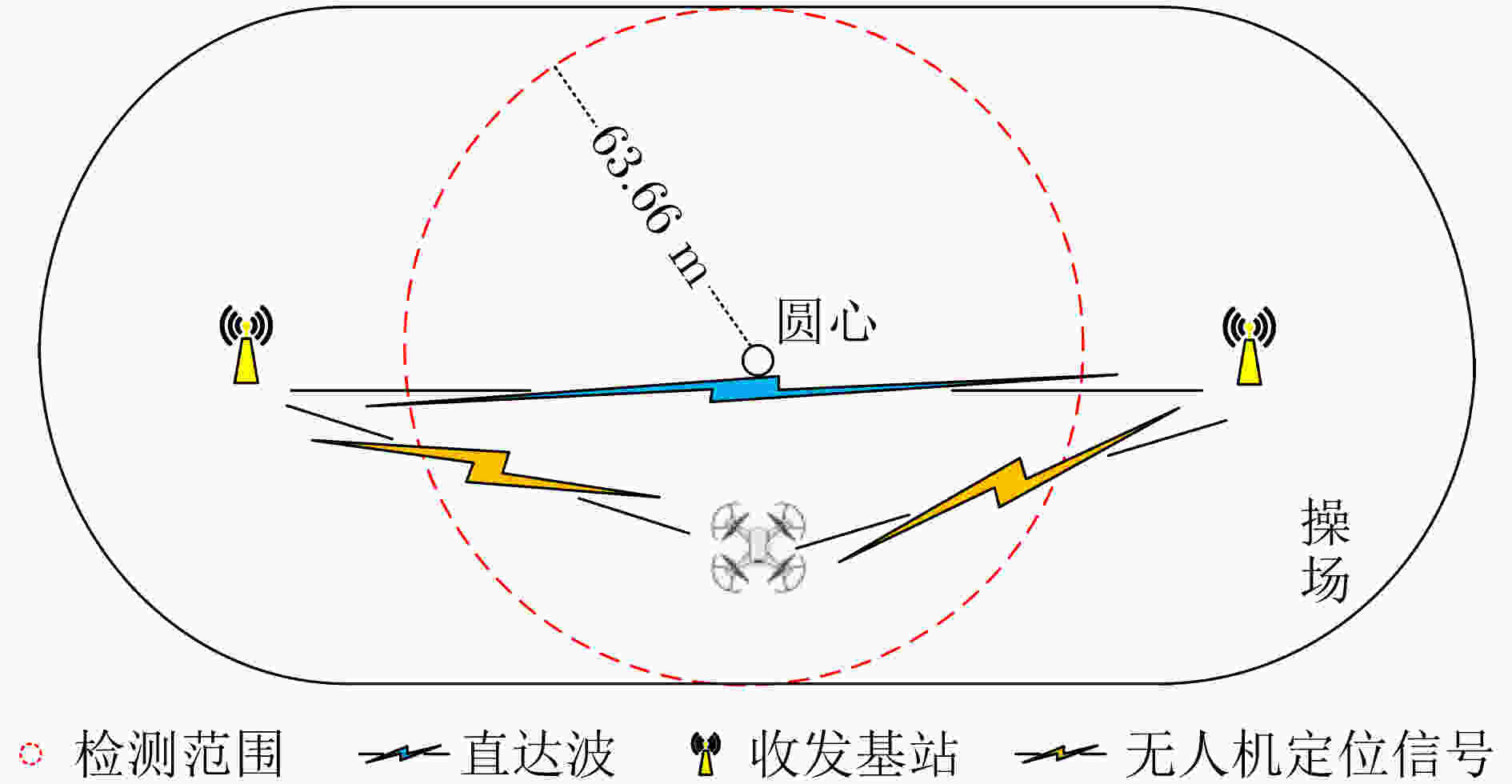
参数 值 参数 值 参数 值 基站距离 300 m 信号功率 0.08 W 载波频率 2 GHz 目标反射面积 0.02 m2 FFT点数 2048 接收机采样率 15 MHz 表 3 SVM模型准确率
训练集/数据集:0.6 训练集/数据集:0.7 查全率 0.968 查全率 0.957 查准率 0.953 查准率 0.966 -
[1] QU Yaohong, WU Jizhi, XIAO Bing, et al. A fault-tolerant cooperative positioning approach for multiple UAVs[J]. IEEE Access, 2017, 5: 15630–15640. doi: 10.1109/ACCESS.2017.2731425 [2] GALKIN B, KIBIŁDA J, and DASILVA L A. A stochastic model for UAV networks positioned above demand hotspots in urban environments[J]. IEEE Transactions on Vehicular Technology, 2019, 68(7): 6985–6996. doi: 10.1109/TVT.2019.2916429 [3] PENG Jing, ZHANG Ping, ZHENG Lanxiang, et al. UAV positioning based on multi-sensor fusion[J]. IEEE Access, 2020, 8: 34455–34467. doi: 10.1109/ACCESS.2020.2974285 [4] ZHU Yuhong, MA Tengfei, LI Zhijun, et al. NLOS identification and correction based on multidimensional scaling and quasi-accurate detection[J]. IEEE Access, 2019, 7: 53977–53987. doi: 10.1109/ACCESS.2019.2906866 [5] WU Shixun, ZHANG Shengjun, and HUANG Darong. A TOA-based localization algorithm with simultaneous NLOS mitigation and synchronization error elimination[J]. IEEE Sensors Letters, 2019, 3(3): 1–4. doi: 10.1109/LSENS.2019.2897924 [6] GUO Qing, KE Wei, and TANG Wanchun. Wireless positioning method based on dynamic objective function under mixed LOS/NLOS conditions[C]. 2018 Ubiquitous Positioning, Indoor Navigation and Location-Based Services (UPINLBS), Wuhan, China, 2018: 1–4. doi: 10.1109/UPINLBS.2018.8559838. [7] YU Xiaohan, CHEN Xiaolong, HUANG Yong, et al. Radar moving target detection in clutter background via adaptive dual-threshold sparse Fourier transform[J]. IEEE Access, 2019, 7: 58200–58211. doi: 10.1109/ACCESS.2019.2914232 [8] 马济通, 邱天爽, 李蓉, 等. 脉冲噪声下基于Renyi熵的分数低阶双模盲均衡算法[J]. 电子与信息学报, 2018, 40(2): 378–385. doi: 10.11999/JEIT170366MA Jitong, QIU Tianshuang, LI Rong, et al. Dual-mode blind equalization algorithm based on Renyi entropy and fractional lower order statistics under impulsive noise[J]. Journal of Electronics &Information Technology, 2018, 40(2): 378–385. doi: 10.11999/JEIT170366 [9] 蔡睿妍, 杨力, 钱杨. 脉冲噪声下基于相关熵的相干分布源DOA估计新方法[J]. 电子与信息学报, 2020, 42(11): 2600–2606. doi: 10.11999/JEIT200325CAI Ruiyan, YANG Li, and QIAN Yang. A novel DOA estimation method for coherently distributed sources based on correntropy in the impulsive noise[J]. Journal of Electronics &Information Technology, 2020, 42(11): 2600–2606. doi: 10.11999/JEIT200325 [10] ZHAO Yongsheng, HU Dexiu, Zhao Yongjun, et al. Multipath TDOA and FDOA estimation in passive Bistatic radar via multiple signal classification[C]. The 20th International Radar Symposium (IRS), Ulm, Germany, 2019: 1–6. doi: 10.23919/IRS.2019.8768128. [11] CHENG Lan, WANG Kai, REN M F, et al. Comprehensive analysis of multipath estimation algorithms in the framework of information theoretic learning[J]. IEEE Access, 2018, 6: 5521–5530. doi: 10.1109/ACCESS.2018.2793896 [12] KHAN U, YE Yunxing, AISHA A U, et al. Precision of EM simulation based wireless location estimation in multi-sensor capsule endoscopy[J]. IEEE Journal of Translational Engineering in Health and Medicine, 2018, 6: 1–11. doi: 10.1109/JTEHM.2018.2818177 [13] WANG Boyuan, GAN Xingli, LIU Xuelin, et al. A novel weighted KNN algorithm based on RSS similarity and position distance for Wi-Fi fingerprint positioning[J]. IEEE Access, 2020, 8: 30591–30602. doi: 10.1109/ACCESS.2020.2973212 [14] KHOUZANI M and MALACARIA P. Optimal channel design: A game theoretical analysis[J]. Entropy, 2018, 20(9): 675. doi: 10.3390/e20090675 [15] ZHOU Di, ZHUANG Xiao, ZUO Hongfu, et al. Deep learning-based approach for civil aircraft hazard identification and prediction[J]. IEEE Access, 2020, 8: 103665–103683. doi: 10.1109/ACCESS.2020.2997371 [16] SUN Xiankun, LIU Lan, LI Chengfan, et al. Classification for remote sensing data with improved CNN-SVM method[J]. IEEE Access, 2019, 7: 164507–164516. doi: 10.1109/ACCESS.2019.2952946 [17] BAO Jianrong, NIE Jianyuan, LIU Chao, et al. Improved blind spectrum sensing by covariance matrix Cholesky decomposition and RBF-SVM decision classification at low SNRs[J]. IEEE Access, 2019, 7: 97117–97129. doi: 10.1109/ACCESS.2019.2929316 [18] WU Xiaohe, ZUO Wangmeng, LIN Liang, et al. F-SVM: Combination of feature transformation and SVM learning via convex relaxation[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(11): 5185–5199. doi: 10.1109/TNNLS.2018.2791507 -





 下载:
下载:


 下载:
下载:
