A Parameter Estimation Method for Sub-Nyquist Sampled Radar Signals Based on Frequency-domain Delay-Doppler Two-dimensional Focusing
-
摘要: 针对欠采样脉冲多普勒雷达信号参数估计中已有方法抗噪性差、顺序参数估计方法中后续参数估计受前面参数估计精度影响严重等问题,该文提出一种基于有限新息率(Finite Rate of Innovation, FRI)采样的频域时延-多普勒2维聚焦(FD2TF)算法。在该算法中,利用FRI采样结构能够以低于奈奎斯特采样频率的速率获得信号的一系列傅里叶系数,通过频域2维聚焦过程能够同时估计时延和多普勒参数,避免了参数顺序估计中误差累积的问题,理论分析证明了该算法能够大幅提升采样信号的信噪比,提高算法抗噪性和鲁棒性。在2维聚焦算法的基础上该文还提出了基于逆傅里叶变换的2维聚焦简化算法,在提高参数估计网格密度的同时,大大减低了2维聚焦算法的计算量。仿真和对比实验结果证明了该方法的有效性和良好的抗噪性。Abstract: In the problem of sub-Nyquist sampled pulse Doppler radar signals, the existing methods have poor anti-noise performance, and the subsequent parameter estimation in the sequential parameter estimation methods is seriously affected by the accuracy of the previous parameter estimation. A Frequency-domain Delay-Doppler Two-dimensional Focusing (FD2TF) algorithm is proposed based on Finite Rate of Innovation (FRI) sampling method to solve the problem. The algorithm can obtain a series of Fourier coefficients of the signal at a sampling rate lower than the Nyquist sampling frequency through the FRI sampling structure. The time delay and Doppler parameters can be estimated simultaneously through the frequency-domain two-dimensional focusing process, and the problem of error accumulation in parameter sequential estimation methods can be avoided. Theoretical analysis proves that the algorithm can greatly improve the signal-to-noise ratio of the sampled signal, and improve the anti-noise performance and robustness of the algorithm. This paper also proposes a two-dimensional focusing simplification algorithm based on inverse Fourier transform, which greatly reduces the computational complexity of the two-dimensional focusing algorithm while increasing the grid density of parameter estimation. Simulation and comparative experiment results show that the proposed method is effective and has good anti-noise performance.
-
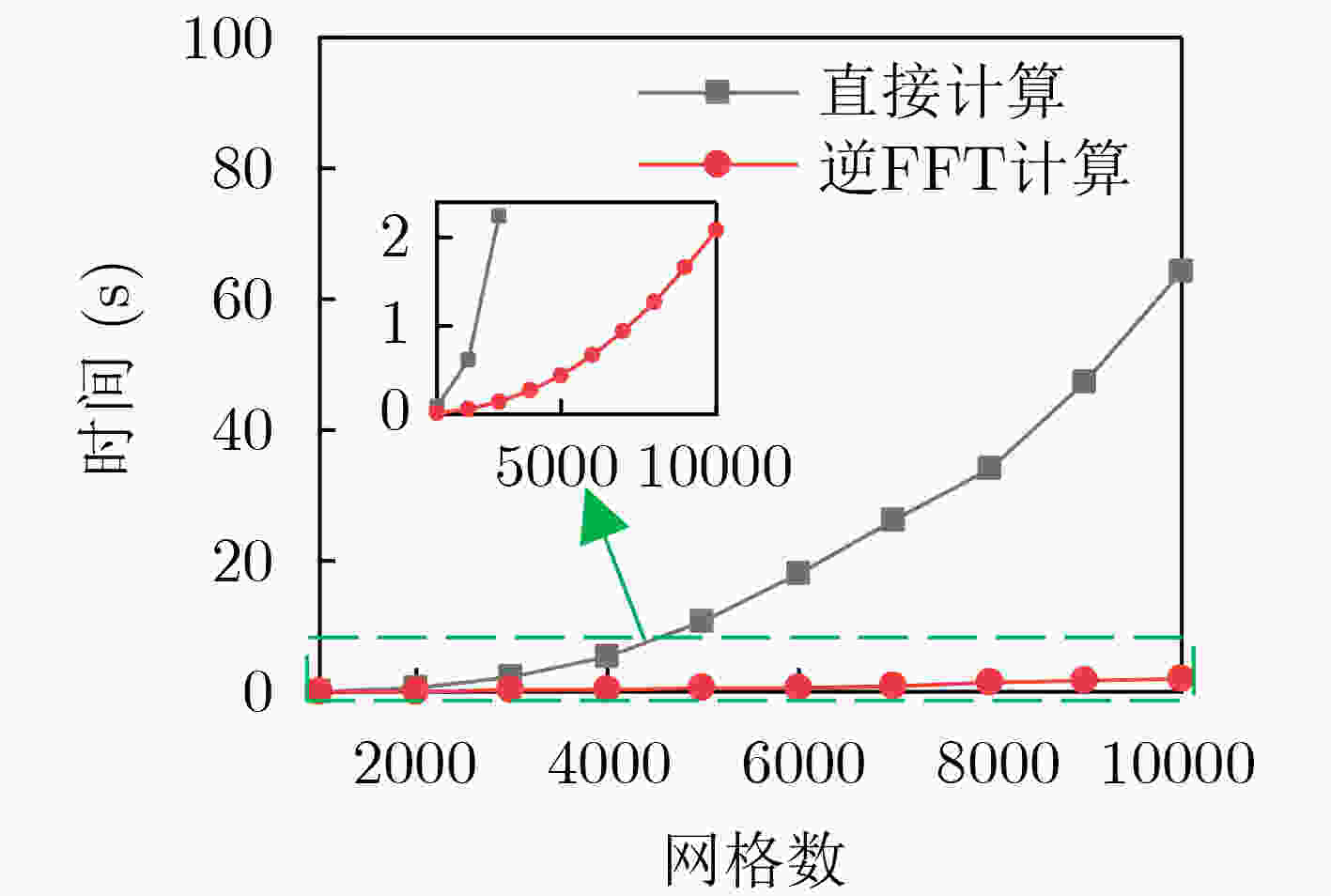
表 1 直接多普勒聚焦与逆FFT方法计算量对比
方法 直接多普勒聚焦计算 逆FFT计算 复数乘法次数 $MQ(M + Q)$ $\dfrac{ {MQ} }{2}({\log _2}M + {\log _2}Q)$ 复数加法次数 $MQ(M + Q - 2)$ $MQ({\log _2}M + {\log _2}Q)$ 表 2 脉冲-多普勒2维聚焦算法雷达信号参数估计过程(算法1)
输入 傅里叶系数${Y_p}[k]$;PRI数$P$;每个PRI采集傅里叶系数个数
$K$;脉冲重复间隔$T$;目标个数$L$。输出 信号参数$\left\{ {{a_l},{\tau _l},{v_l}} \right\}_{l = 0}^{L - 1}$。 步骤 1:根据式(14)~(16)完成采样数据插值及时延-多普勒2维
聚焦过程。2:根据式(10)计算目标幅值${\tilde a_l}$。 3:根据式(11)确定信号的时延和多普勒参数$({\tilde \tau _l},{\tilde v_l})$。 4:根据式(13)去除已估计目标信号对其他目标参数估计的
影响。5:重复步骤3~5直到获得所有$L$个目标参数。 6:输出估计参数$\left\{ {{{\tilde a}_l},{{\tilde \tau }_l},{{\tilde v}_l}} \right\}_{l = 0}^{L - 1}$。 -
[1] ALABASTER C, 著. 张伟, 刘洪亮, 刘朋, 等译. 脉冲多普勒雷达——原理、技术与应用[M]. 北京: 电子工业出版社, 2016.ALABASTER C, Write, ZHANG Wei, LIU Hongliang, LIU Peng, et al., translation. Pulse Doppler Radar—Principles, Technology, Applications[M]. Beijing: Publishing House of Electronics Industry, 2016. [2] 曹成虎, 赵永波, 索之玲, 等. 基于频谱校正的中国余数定理多普勒频率估计算法[J]. 电子与信息学报, 2019, 41(12): 2903–2910. doi: 10.11999/JEIT181102CAO Chenghu, ZHAO Yongbo, SUO Zhiling, et al. Doppler frequency estimation method based on Chinese Remainder Theorem with spectrum correction[J]. Journal of Electronics &Information Technology, 2019, 41(12): 2903–2910. doi: 10.11999/JEIT181102 [3] 李迎春, 王国宏, 关成斌, 等. 速度拖引干扰和杂波背景下脉冲多普勒雷达目标跟踪算法[J]. 电子与信息学报, 2015, 37(4): 989–994. doi: 10.11999/JEIT140856LI Yingchun, WANG Guohong, GUAN Chengbin, et al. Algorithm for target tracking with pulse Doppler radar in the presence of velocity gate pull off/in jamming and clutter environment[J]. Journal of Electronics &Information Technology, 2015, 37(4): 989–994. doi: 10.11999/JEIT140856 [4] CANDES E J, ROMBERG J, and TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489–509. doi: 10.1109/TIT.2005.862083 [5] 马彬, 王宏明, 谢显中. 基于二项分布改进的宽带压缩频谱检测方案[J]. 电子学报, 2020, 48(2): 243–248. doi: 10.3969/j.issn.0372-2112.2020.02.003MA Bin, WANG Hongming, and XIE Xianzhong. An improved wideband compressed spectrum sensing scheme based on binomial distribution[J]. Acta Electronica Sinica, 2020, 48(2): 243–248. doi: 10.3969/j.issn.0372-2112.2020.02.003 [6] 张波, 刘郁林, 王开. 稀疏随机矩阵有限等距性质分析[J]. 电子与信息学报, 2014, 36(1): 169–174. doi: 10.3724/SP.J.1146.2013.00023ZHANG Bo, LIU Yulin, and WANG Kai. Restricted isometry property analysis for sparse random matrices[J]. Journal of Electronics &Information Technology, 2014, 36(1): 169–174. doi: 10.3724/SP.J.1146.2013.00023 [7] HERMAN M A and STROHMER T. High-resolution radar via compressed sensing[J]. IEEE Transactions on Signal Processing, 2009, 57(6): 2275–2284. doi: 10.1109/TSP.2009.2014277 [8] ZHANG Jindong, ZHU Daiyin, and ZHANG Gong. Adaptive compressed sensing radar oriented toward cognitive detection in dynamic sparse target scene[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 1718–1729. doi: 10.1109/TSP.2012.2183127 [9] TEKE O, GURBUZ A C, and ARIKAN O. A robust compressive sensing based technique for reconstruction of sparse radar scenes[J]. Digital Signal Processing, 2014, 27: 23–32. doi: 10.1016/j.dsp.2013.12.008 [10] VETTERLI M, MARZILIANO P, and BLU T. Sampling signals with finite rate of innovation[J]. IEEE Transactions on Signal Processing, 2002, 50(6): 1417–1428. doi: 10.1109/TSP.2002.1003065 [11] 王亚军, 李明, 刘高峰. 复杂脉冲序列的有限新息率采样方法[J]. 电子与信息学报, 2013, 35(7): 1606–1611. doi: 10.3724/SP.J.1146.2012.01329WANG Yajun, LI Ming, and LIU Gaofeng. Sampling complex pulse streams with finite rate of innovation methods[J]. Journal of Electronics &Information Technology, 2013, 35(7): 1606–1611. doi: 10.3724/SP.J.1146.2012.01329 [12] 王亚军, 李明, 刘高峰. 基于改进指数再生采样核的有限新息率采样系统[J]. 电子与信息学报, 2013, 35(9): 2088–2093. doi: 10.3724/SP.J.1146.2013.00059WANG Yajun, LI Ming, and LIU Gaofeng. Finite rate of innovation sampling system based on modified exponential reproducing sampling kernel[J]. Journal of Electronics &Information Technology, 2013, 35(9): 2088–2093. doi: 10.3724/SP.J.1146.2013.00059 [13] BAJWA W U, GEDALYAHU K, and ELDAR Y C. Identification of parametric underspread linear systems and super-resolution radar[J]. IEEE Transactions on Signal Processing, 2011, 59(6): 2548–2561. doi: 10.1109/TSP.2011.2114657 [14] BAR-ILAN O and ELDAR Y C. Sub-Nyquist radar via Doppler focusing[J]. IEEE Transactions on Signal Processing, 2014, 62(7): 1796–1811. doi: 10.1109/TSP.2014.2304917 [15] CHEN Shengyao, XI Feng, and LIU Zhong. A general sequential delay-Doppler estimation scheme for sub-Nyquist pulse-Doppler radar[J]. Signal Processing, 2017, 135: 210–217. doi: 10.1016/j.sigpro.2017.01.012 [16] CHEN Shengyao, XI Feng, and LIU Zhong. A general and yet efficient scheme for sub-Nyquist radar processing[J]. Signal Processing, 2018, 142: 206–211. doi: 10.1016/j.sigpro.2017.07.018 [17] SKOLNIK M I. Radar Handbook[M]. New York: McGraw-Hill, 1970. [18] GEDALYAHU K, TUR R, and ELDAR Y C. Multichannel sampling of pulse streams at the rate of innovation[J]. IEEE Transactions on Signal Processing, 2011, 59(4): 1491–1504. doi: 10.1109/TSP.2011.2105481 [19] ITZHAK G, BARANSKY E, WAGNER N, et al. A hardware prototype for sub-Nyquist radar sensing[C]. SCC 2013; 9th International ITG Conference on Systems, Communication and Coding, Munich, Germany, 2013: 1–6. [20] BARANSKY E, ITZHAK G, WAGNER N, et al. Sub-Nyquist radar prototype: Hardware and algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 809–822. doi: 10.1109/TAES.2014.120475 -





 下载:
下载:




 下载:
下载:
