A Four Cumulant-Based Direction Finding Method for Bistatic MIMO Radar with Mutual Coupling
-
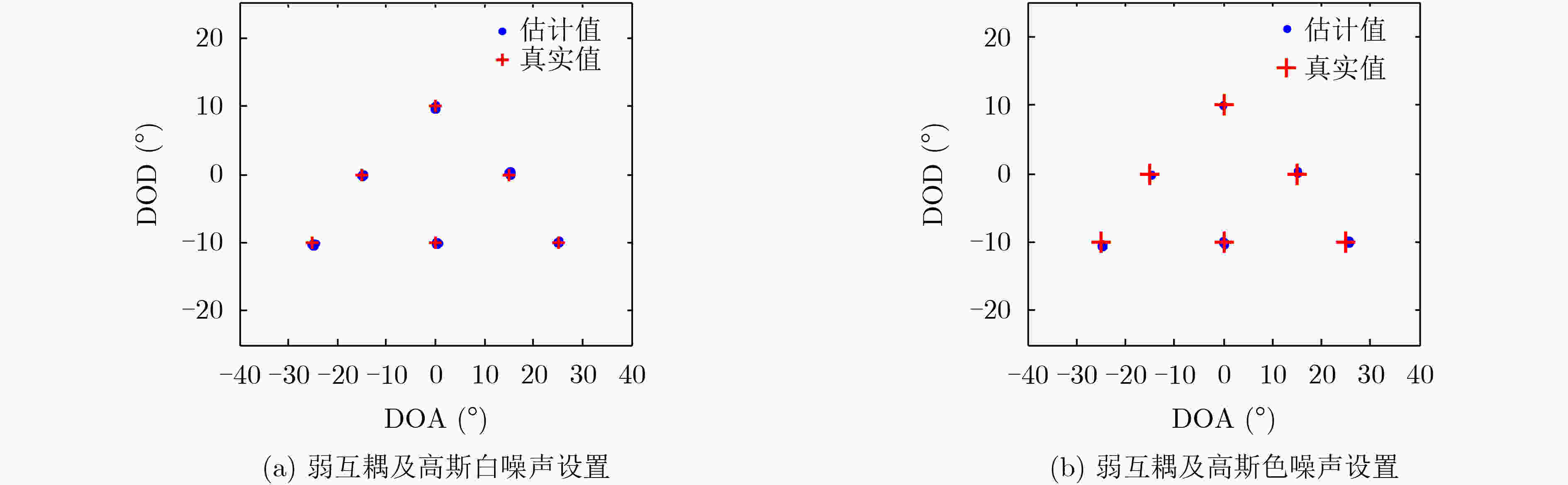
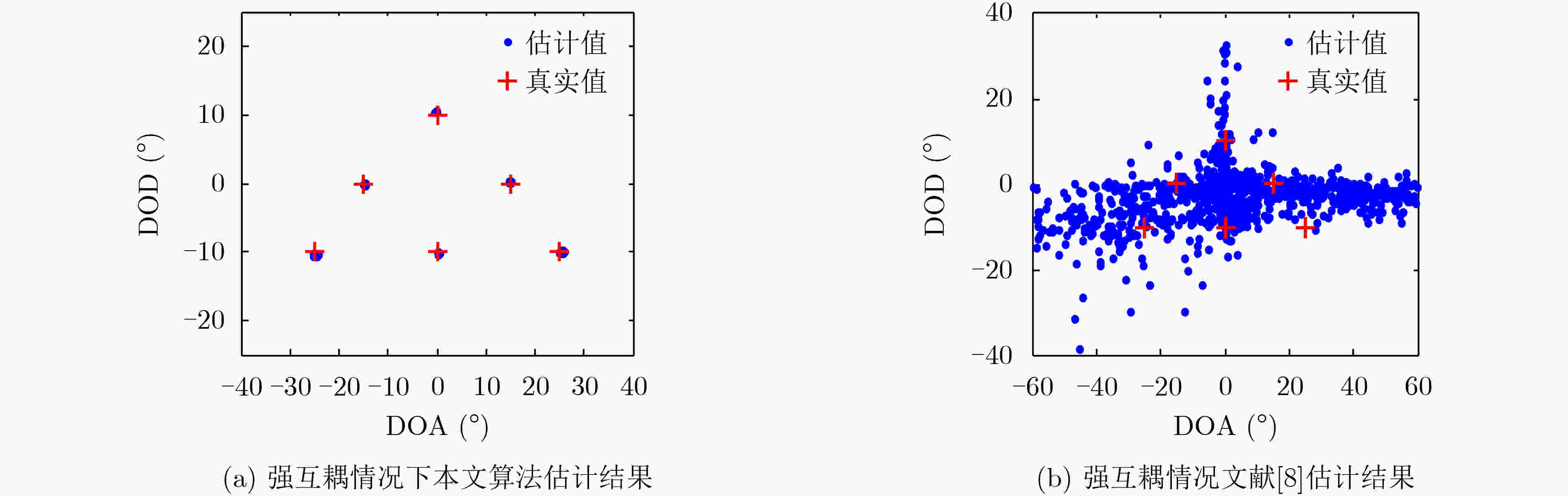
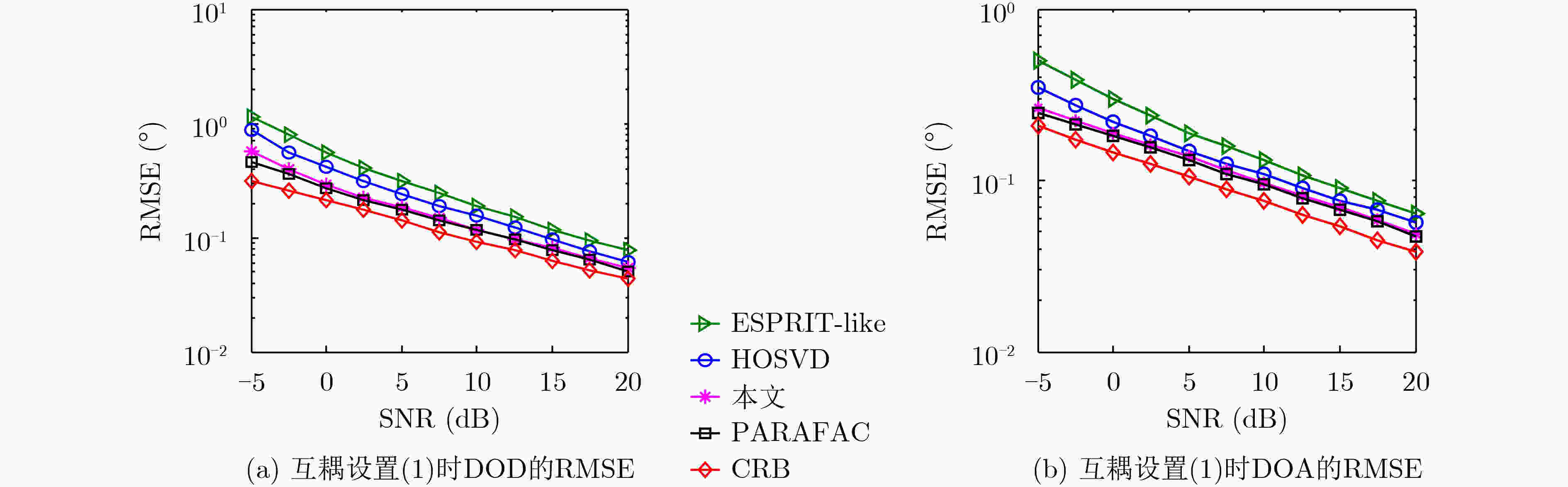
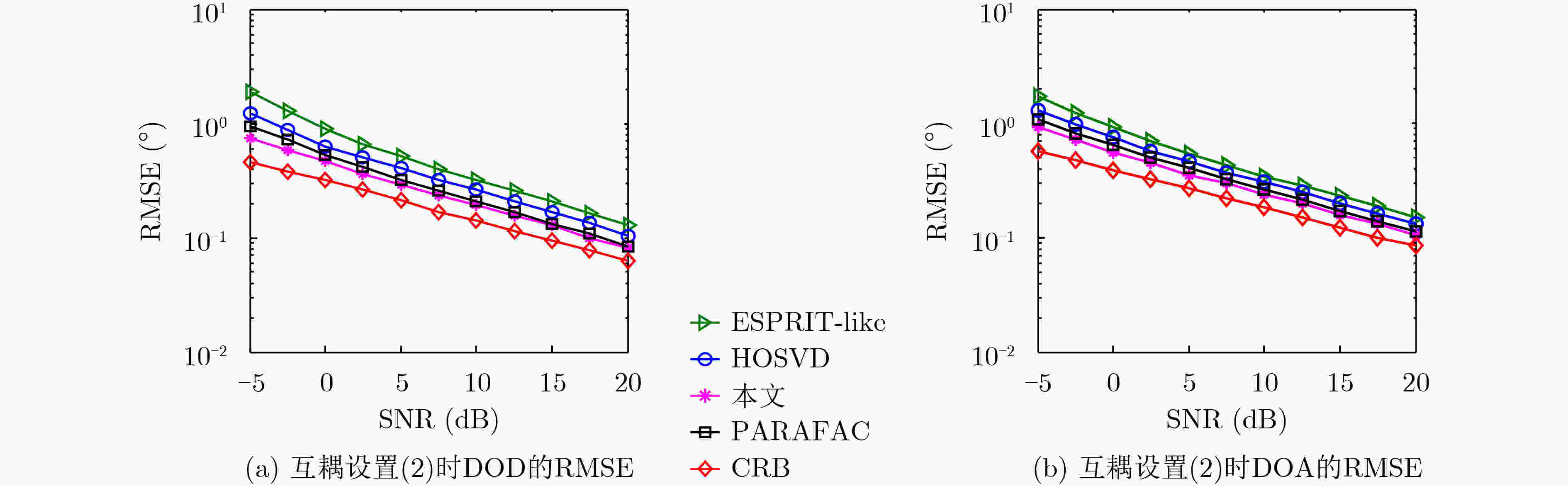
摘要: 发射和接收阵列的互耦效应将使得双基地多输入多输出(MIMO)雷达的角度估计算法性能下降。针对阵列互耦效应和高斯色噪声并存情况,该文提出一种基于4阶累积量组合矩阵构造的收发角度估计方法。该方法首先根据收发互耦矩阵的Kronecker乘积特点,并结合互耦矩阵带状、对称的Toeplitz变换性质,充分利用所有的接收数据,构造出多组发射和接收4阶累积量矩阵,通过组合收发累积量矩阵进一步构造出4阶块累积量矩阵,并利用矩阵的奇异值分解,提取出发射和接收旋转不变因子。理论和仿真结果表明:在强互耦效应情况下,所提算法能够有效估计出高斯色噪声背景下目标的收发角度,并实现自动配对。在强互耦情况下,所提算法的估计性能优于其他算法。Abstract: The mutual coupling effects of the transmitter and receiver are known to degrade the performance of direction finding for a bistatic Multiple Input Multiple Output (MIMO) radar system. A four cumulant-combinatorial matrix-based algorithm is proposed to estimate jointly the Direction Of Departure (DOD)and Direction Of Arrival (DOA) of targets under the coexistences of unknown mutual coupling and Gaussian colored noise. Firstly, the multiple groups of four cumulant matrices both on transmitter and receiver are constructed by using the Kronecker product and the banded symmetric Toeplitz characteristics of the mutual coupling matrices. The block four-cumulant matrix is further constructed by combining the transmitter and receiver four cunmulant matrices. Then the new matrix is combined to extract the transmit and receive shift invariance matrices by using the transmitter and receiver four cumulant matrices. The results illustrate that: The proposed method can estimate the DOD and DOA of the targets efficiently in the presence of the strong mutual coupling effect, and parameters are paired automatically without extra pairing operation. The parameter estimation performance of the proposed method is better than those of the existing methods under the strong mutual coupling effect conditions.
-
图 2 强互耦情况本文算法与文献[8]的目标定位结果
-
[1] CAO Mingyang, VOROBYOV S A, and HASSANIEN A. Transmit array interpolation for DOA estimation via tensor decomposition in 2-D MIMO radar[J]. IEEE Transactions on Signal Processing, 2017, 65(19): 5225–5239. doi: 10.1109/TSP.2017.2721904 [2] 徐保庆, 赵永波, 庞晓娇. 基于实值处理的联合波束域双基地MIMO雷达测角算法[J]. 电子与信息学报, 2019, 41(7): 1721–1727. doi: 10.11999/JEIT180766XU Baoqing, ZHAO Yongbo, and PANG Xiaojiao. Joint real-valued beamspace-based method for angle estimation in bistatic MIMO radar[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1721–1727. doi: 10.11999/JEIT180766 [3] 程院兵, 吴临江, 郑昱, 等. 基于多维范德蒙德结构的双基地MIMO雷达收发角及多普勒频率联合估计[J]. 电子与信息学报, 2018, 40(9): 2258–2264. doi: 10.11999/JEIT171002CHENG Yuanbing, WU Linjiang, ZHENG Yu, et al. Multi-dimensional Vandermonde structure based DOD-DOA and Doppler frequency estimation for bistatic MIMO radar[J]. Journal of Electronics &Information Technology, 2018, 40(9): 2258–2264. doi: 10.11999/JEIT171002 [4] GUO Yiduo and FENG Weike. Low-complexity angle estimation for noncircular signals in bistatic MIMO radar[J]. IEICE Transactions on Communications, 2017, E100. B(6): 997–1002. doi: 10.1587/transcom.2016EBP3259 [5] MÉRIAUX B, ZHANG Xin, KORSO M N E, et al. Iterative marginal maximum likelihood DOD and DOA estimation for MIMO radar in the presence of SIRP clutter[J]. Signal Processing, 2019, 155: 384–390. doi: 10.1016/j.sigpro.2018.09.034 [6] LIU Xiaoli and LIAO Guisheng. Direction finding and mutual coupling estimation for bistatic MIMO radar[J]. Signal Processing, 2012, 92(2): 517–522. doi: 10.1016/j.sigpro.2011.08.017 [7] ZHENG Zhidong, ZHANG Jin, and ZHANG Jianyun. Joint DOD and DOA estimation of bistatic MIMO radar in the presence of unknown mutual coupling[J]. Signal Processing, 2012, 92(12): 3039–3048. doi: 10.1016/j.sigpro.2012.06.013 [8] 杨康, 文方青, 黄冬梅, 等. 基于实值三线性分解的互耦条件下双基地MIMO雷达角度估计算法[J]. 系统工程与电子技术, 2018, 40(2): 314–321. doi: 10.3969/j.issn.1001-506X.2018.02.12YANG Kang, WEN Fangqing, HUANG Dongmei, et al. Real-value-based trilinear decomposition-based direction estimation algorithm for bistatic MIMO radar in the presence of mutual coupling[J]. Systems Engineering and Electronics, 2018, 40(2): 314–321. doi: 10.3969/j.issn.1001-506X.2018.02.12 [9] WANG Xianpeng, WANG Wei, LIU Jing, et al. Tensor-based real-valued subspace approach for angle estimation in bistatic MIMO radar with unknown mutual coupling[J]. Signal Processing, 2015, 116: 152–158. doi: 10.1016/j.sigpro.2015.03.020 [10] 郑志东, 张剑云, 康凯, 等. 互耦条件下双基地MIMO雷达的收发角度估计[J]. 中国科学: 信息科学, 2013, 43(6): 784–797.ZHENG Zhidong, ZHANG Jianyun, KANG kai, et al. Joint DOD and DOA estimation for bistatic MIMO radar in the presence of mutual coupling[J]. Science China:Information Science, 2013, 43(6): 784–797. [11] 杨守国, 李勇, 张昆辉, 等. 基于降维的双基地MIMO雷达收发阵列互耦和幅相误差校正算法[J]. 系统工程与电子技术, 2018, 40(12): 2668–2674. doi: 10.3969/j.issn.1001-506X.2018.12.08YANG Shouguo, LI Yong, ZHANG Kunhui, et al. Reduced dimensional calibration method for bistatic MIMO radar with mutual coupling and gain-phase errors of transmitting and receiving arrays[J]. Systems Engineering and Electronics, 2018, 40(12): 2668–2674. doi: 10.3969/j.issn.1001-506X.2018.12.08 [12] 王咸鹏, 国月皓, 黄梦醒, 等. 互耦条件下MIMO雷达非圆目标稳健角度估计方法[J]. 通信学报, 2019, 40(7): 144–150. doi: 10.11959/j.issn.1000-436x.2019163WANG Xianpeng, GUO Yuehao, HUANG Mengxing, et al. Robust angle estimation method for noncircular targets in MIMO radar with mutual coupling[J]. Journal on Communications, 2019, 40(7): 144–150. doi: 10.11959/j.issn.1000-436x.2019163 [13] WEN Fangqing, ZHANG Zijing, WANG Ke, et al. Angle estimation and mutual coupling self-calibration for ULA-based bistatic MIMO radar[J]. Signal Processing, 2018, 144: 61–67. doi: 10.1016/j.sigpro.2017.09.021 [14] LIAO Bin, ZHANG Zhiguo, and CHAN S C. DOA estimation and tracking of ULAs with mutual coupling[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 891–905. doi: 10.1109/TAES.2012.6129676 [15] GOLUB G H and VAN LOAN C F. Matrix Computations[M]. Baltimore: Johns Hopkins University Press, 1996: 125–129. -





 下载:
下载:


 下载:
下载:
