Integration of WiFi, Laser, and Map for Robot Indoor Localization
-
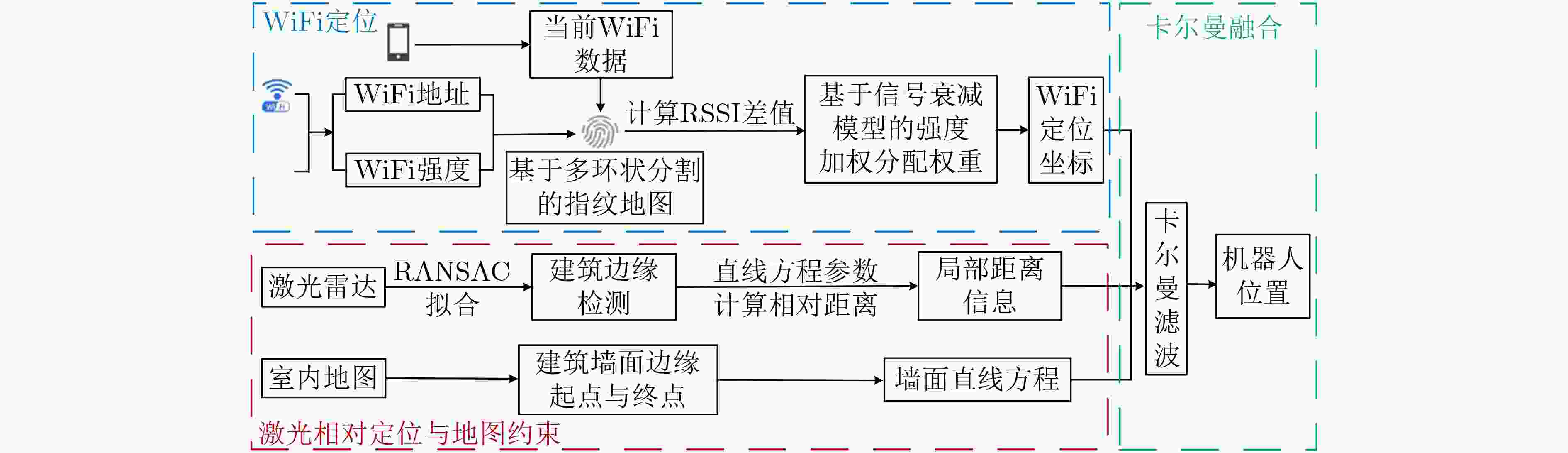
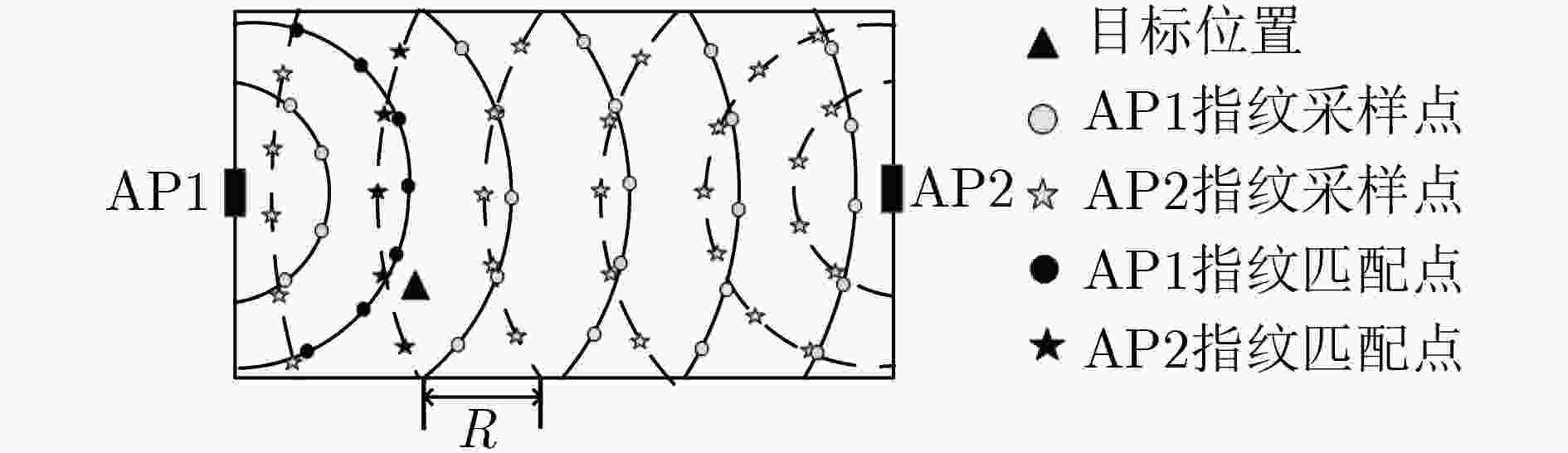
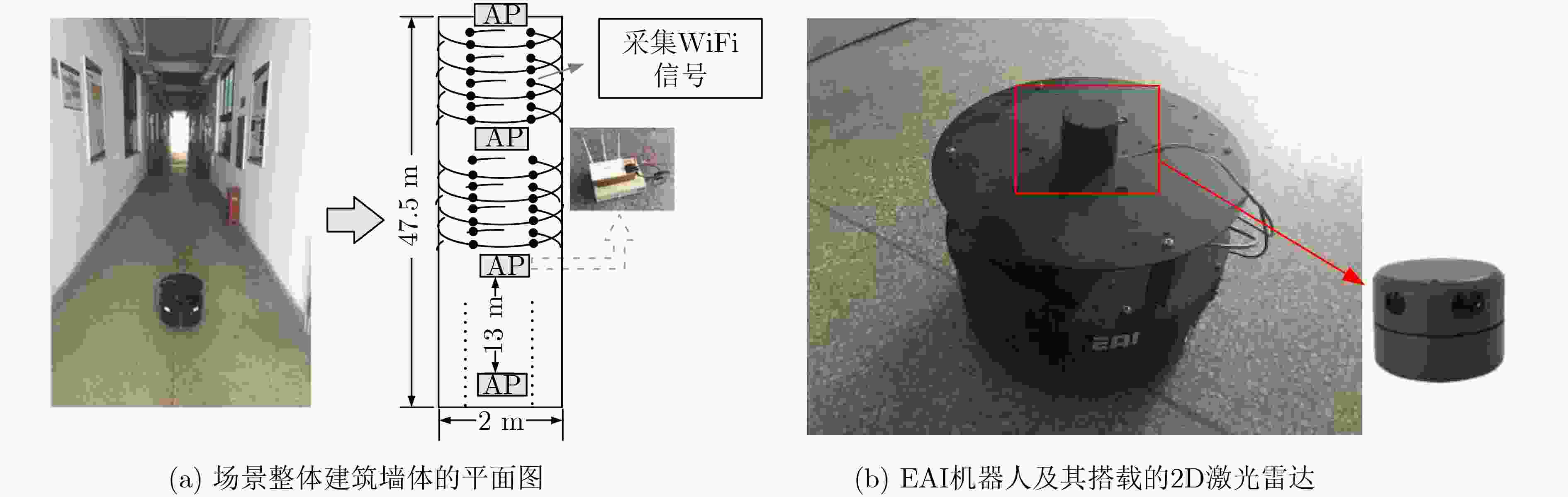
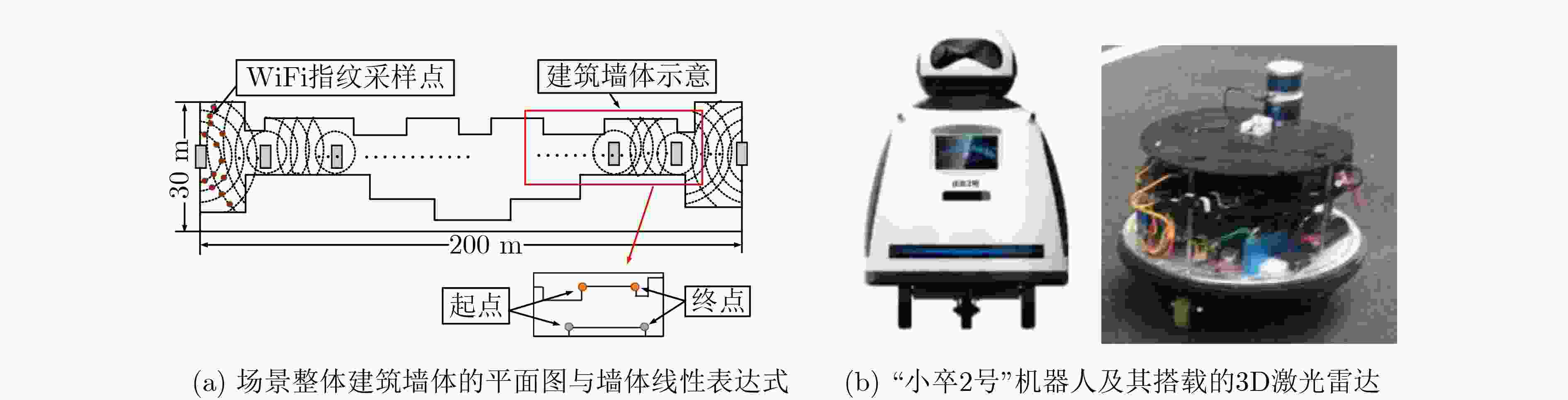
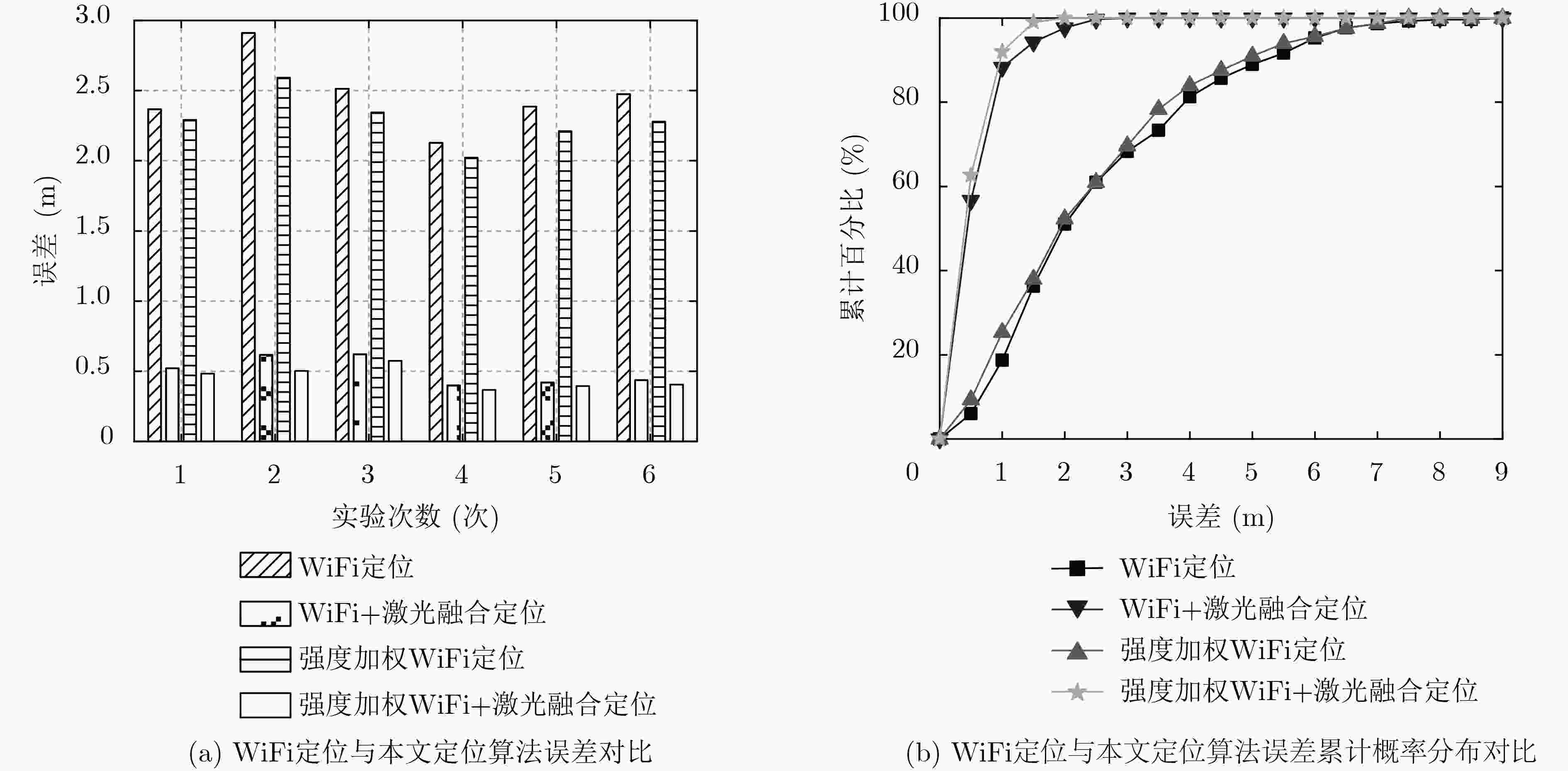
摘要: 由于室内环境受多径效应影响,单一WiFi定位效果不佳;激光雷达(LiDAR)虽然测距定位精度高,但在室内存在大量单一、重复的场景结构(如走廊)时,往往会由于无法提取有效特征进行匹配而造成大量错误定位。因此,该文提出基于卡尔曼滤波框架的WiFi、激光雷达与地图的融合定位新方法。其中,滤波器的状态定义为机器人当前与历史时刻的位置序列。滤波器的观测值由两部分组成,一部分为该文所提基于多环路分割地图下信号强度加权匹配的WiFi指纹定位结果;另一部分来自激光雷达在单一重复场景中计算出来的高精度相对定位结果(如横向定位)。利用场景地图中的先验参考位置,可将该横向定位结果转变为机器人位置的线性约束。最后,利用卡尔曼滤波器实现机器人高精度的融合定位结果。实验中,针对两种典型的单一、重复的室内场景,分别采用2维与3维激光雷达对该文算法进行验证。实验结果表明,由于激光横向定位精度可达厘米级,结合厘米级地图可以极大提高机器人定位精度。与单一WiFi定位算法相比,利用激光雷达计算出来的相对定位结果结合场景地图,平均定位误差可降低70%~80%,在满足机器人实时定位需求情况下,实现定位精度与稳定性的显著提升。Abstract: WiFi-based localization methods suffer from multipath problem in indoor environments, which leads to poor accuracy. Light Detection And Ranging(LiDAR)-based localization methods can have good accuracy. However, they are not feasible in simple and repetitive scenarios as it is difficult for scene feature extraction and matching. Therefore, a novel localization method to fuse WiFi, LiDAR and Map by integrating them into a Kalman filter framework is proposed. In this framework, the state of the filter is defined as the current and historical position sequence of the robot. The observation consists of two parts. The first is the WiFi fingerprint localization results based on the proposed distance-weighted WiFi fingerprint matching method on multi-loop segmentation map; The second part comes from the high-precision relative localization results (such as lateral localization) by LiDAR in a single repeated scene. By utilizing the priori reference position in the scene map, such lateral positioning result can be integrated with the map to formulate linear constraints on the robot position. Finally, the Kalman filter is applied to accurate localization of the robot. The proposed algorithm is verified in two scenarios, where 2D and 3D LiDAR are applied. Experimental results show the average localization error of the proposed algorithm can be reduced by 70%~80%, which demonstrate that proposed method can improve the localization accuracy and stability.
-
Key words:
- Map-based localization /
- Robot /
- Kalman filter /
- Light Detection And Ranging(LiDAR) /
- WiFi fingerprint
-
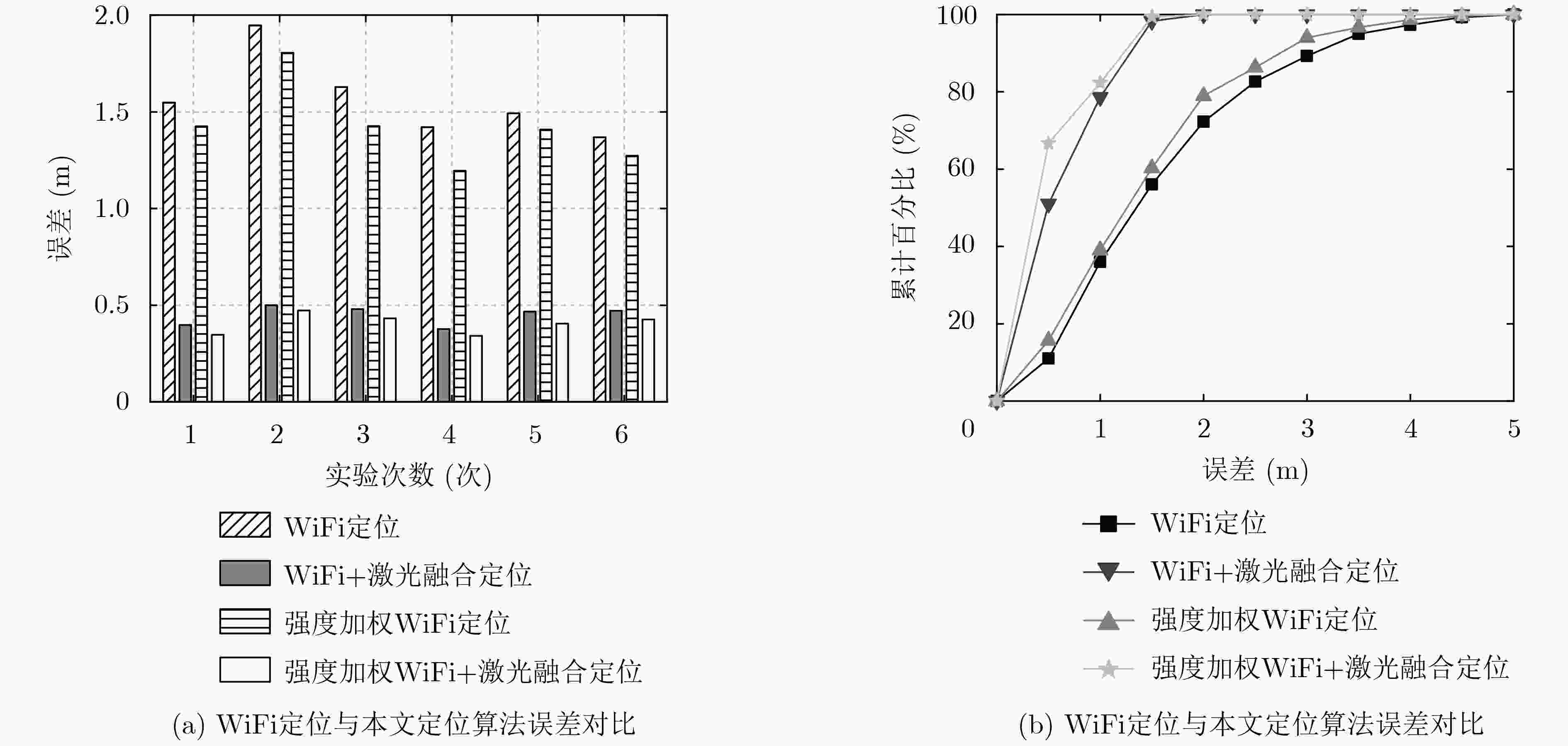
表 1 单一WiFi指纹结合卡尔曼滤波前后定位结果对比
算法 最大误差(m) 平均误差(m) WiFi定位 4.97 1.57 WiFi+卡尔曼定位 4.26 1.32 强度加权WiFi定位 4.29 1.42 强度加权WiFi+卡尔曼定位 3.85 1.18 表 2 单一WiFi指纹结合卡尔曼滤波前后结果对比
算法 最大误差(m) 平均误差(m) WiFi定位 9.37 2.46 WiFi+卡尔曼定位 8.61 2.10 强度加权WiFi定位 8.14 2.28 强度加权WiFi+卡尔曼定位 7.38 1.92 -
[1] 胡久松, 刘宏立, 肖郭璇, 等. 应用于WiFi室内定位的自适应仿射传播聚类算法[J]. 电子与信息学报, 2018, 40(12): 2889–2895. doi: 10.11999/JEIT180186HU Jiusong, LIU Hongli, XIAO Guoxuan, et al. Adaptive affine propagation clustering algorithm for WiFi indoor positioning[J]. Journal of Electronics &Information Technology, 2018, 40(12): 2889–2895. doi: 10.11999/JEIT180186 [2] 刘国忠, 胡钊政. 基于SURF和ORB全局特征的快速闭环检测[J]. 机器人, 2017, 39(1): 36–45. doi: 10.13973/j.cnki.robot.2017.0036LIU Guozhong and HU Zhaozheng. Fast loop closure detection based on holistic features from SURF and ORB[J]. Robot, 2017, 39(1): 36–45. doi: 10.13973/j.cnki.robot.2017.0036 [3] WANG Yunting, PENG Chaochung, RAVANKAR A A, et al. A single LiDAR-based feature fusion indoor localization algorithm[J]. Sensors (Basel) , 2018, 18(4): 1294. doi: 10.3390/s18041294 [4] 刘文远, 刘慧香, 温丽云, 等. 轻量扩展的射频指纹地图构造方法[J]. 电子与信息学报, 2018, 40(2): 306–313. doi: 10.11999/JEIT170338LIU Wenyuan, LIU Huixiang, WEN Liyun, et al. A scalable lightweight radio fingerprint map construction method[J]. Journal of Electronics &Information Technology, 2018, 40(2): 306–313. doi: 10.11999/JEIT170338 [5] LUO Juan, YIN Xixi, ZHENG Yanliu, et al. Secure indoor localization based on extracting trusted fingerprint[J]. Sensors (Basel) , 2018, 18(2): 469. doi: 10.3390/s18020469 [6] LEU J S, YU M C, and TZENG H J. Improving indoor positioning precision by using received signal strength fingerprint and footprint based on weighted ambient Wi-Fi signals[J]. Computer Networks, 2015, 91: 329–340. doi: 10.1016/j.comnet.2015.08.032 [7] 黄刚, 胡钊政, 蔡浩, 等. 基于Wi-Vi指纹的智能手机室内定位方法[J]. 自动化学报, 2020, 46(2): 320–331. doi: 10.16383/j.aas.2018.c170189HUANG Gang, HU Zhaozheng, CAI Hao, et al. Smartphone-based accurate indoor positioning from Wi-Vi fingerprints[J]. Acta Automatica Sinica, 2020, 46(2): 320–331. doi: 10.16383/j.aas.2018.c170189 [8] CHEN Jiayu, CHEN Hainan, and LUO Xiaowei. Collecting building occupancy data of high resolution based on WiFi and BLE network[J]. Automation in Construction, 2019, 102: 183–194. doi: 10.1016/j.autcon.2019.02.016 [9] LI Zengke, ZHAO Long, QIN Changbiao, et al. WiFi/PDR integrated navigation with robustly constrained Kalman filter[J]. Measurement Science and Technology, 2020, 31(8): 084002. doi: 10.1088/1361-6501/ab87ea [10] RUSINKIEWICZ S and LEVOY M. Efficient variants of the ICP algorithm[C]. The 3rd International Conference on 3-D Digital Imaging and Modeling, Quebec, Canada, 2001: 145–152. doi: 10.1109/IM.2001.924423. [11] ZHANG Ji and SINGH S. LOAM: Lidar odometry and mapping in real-time[C]. Robotics: Science and Systems Conference, Berkeley, USA, 2014: 1–10. doi: 10.15607/RSS.2014.X.007. [12] SHAN Tixiao and ENGLOT B. LeGO-LOAM: Lightweight and ground-optimized lidar odometry and mapping on variable terrain[C]. 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 2018: 4758–4765. doi: 10.1109/IROS.2018.8594299." target="_blank"> 10.1109/IROS.2018.8594299.">doi: 10.1109/IROS.2018.8594299. [13] XUE Weixing, HUA Xianghong, LI Qingquan, et al. A new weighted algorithm based on the uneven spatial resolution of RSSI for indoor localization[J]. IEEE Access, 2018, 6: 26588–26595. doi: 10.1109/ACCESS.2018.2837018 [14] SUNDAR D, SENDIL S, SUBRAMANIAN V, et al. WALE: A weighted adaptive location estimation algorithm[J]. Journal of Ambient Intelligence and Humanized Computing, 2019, 10(7): 2621–2632. doi: 10.1007/s12652-018-0940-y [15] HE Suining and CHAN S H G. INTRI: Contour-based trilateration for indoor fingerprint-based localization[J]. IEEE Transactions on Mobile Computing, 2017, 16(6): 1676–1690. doi: 10.1109/TMC.2016.2604810 -





 下载:
下载:



 下载:
下载:
