An Improved Delay Estimation Algorithm for Underwater Acoustic OFDM Sparse Channel
-
摘要: 水声正交频分复用(OFDM)系统中,采用传统正交匹配追踪(OMP)方法估计离网格(off-grid)时延时,需要很高的过采样因子和高昂的计算开销。针对传统OMP方法估计离网格时延计算复杂度高的问题,该文借鉴多元线性拟合思想引入路径补偿的概念,提出了一种基于路径补偿的改进OMP时延估计算法,用以补偿从离网格路径向其周围网格位置泄漏的能量,并用补偿距离这一参数来解释路径补偿效果。该算法无需增加过采样因子,仅利用恰当的补偿距离即可实现较好的估计效果,且能在提高估计性能的同时降低计算复杂度。仿真分析与海试结果验证了该方法的优越性。Abstract: Traditional Orthogonal Matching Pursuit (OMP) method needs high oversampling factor and computational overhead to estimate off-grid path delays in underwater acoustic Orthogonal Frequency Division Multiplexing (OFDM) systems. In this paper, the idea of path compensation is introduced from multiple linear fitting theory, and an improved OMP path delay estimation method based on path compensation is proposed to reduce the energy leaking from off-grid paths to its surrounding grids. The compensation distance is used to evaluate compensation effect. The improved algorithm can improve the estimation performance by appropriate compensation distance without increasing the oversampling factor. Compared with the traditional OMP method, the proposed algorithm has lower computational complexity but better estimation performance. The results of simulations and sea trial data decoding show the superiority of the proposed method.
-
表 1 内积计算复杂度定性对比
实数乘法 实数加法 OMP-grid-comp $L \cdot 2\lambda {N_{\rm{P}}}{\log _2}\lambda {N_{\rm{P}}}$ $L \cdot 3\lambda {N_{\rm{P}}}{\log _2}\lambda {N_{\rm{P}}}$ OMP-normal-comp $2L \cdot 2\lambda {N_{\rm{P}}}{\log _2}\lambda {N_{\rm{P}}}$ $2L \cdot 3\lambda {N_{\rm{P}}}{\log _2}\lambda {N_{\rm{P}}}$ OMP-sin $2L \cdot 2\lambda {N_{\rm{P}}}{\log _2}\lambda {N_{\rm{P}}}$ $2L \cdot 3\lambda {N_{\rm{P}}}{\log _2}\lambda {N_{\rm{P}}}$ SdMP $L \cdot 2\lambda {N_{\rm{P}}}{\log _2}\lambda {N_{\rm{P}}}$ $L \cdot 3\lambda {N_{\rm{P}}}{\log _2}\lambda {N_{\rm{P}}}$ 表 2 内积计算复杂度定量对比
实数乘法 实数加法 OMP-grid-comp($\lambda = 4$) 102400 153600 OMP-normal-comp($\lambda = 4$) 204800 307200 OMP-sin($\lambda = 4$) 204800 307200 SdMP($\lambda = 4$) 102400 153600 表 3 不同信道估计方法的原始误码率
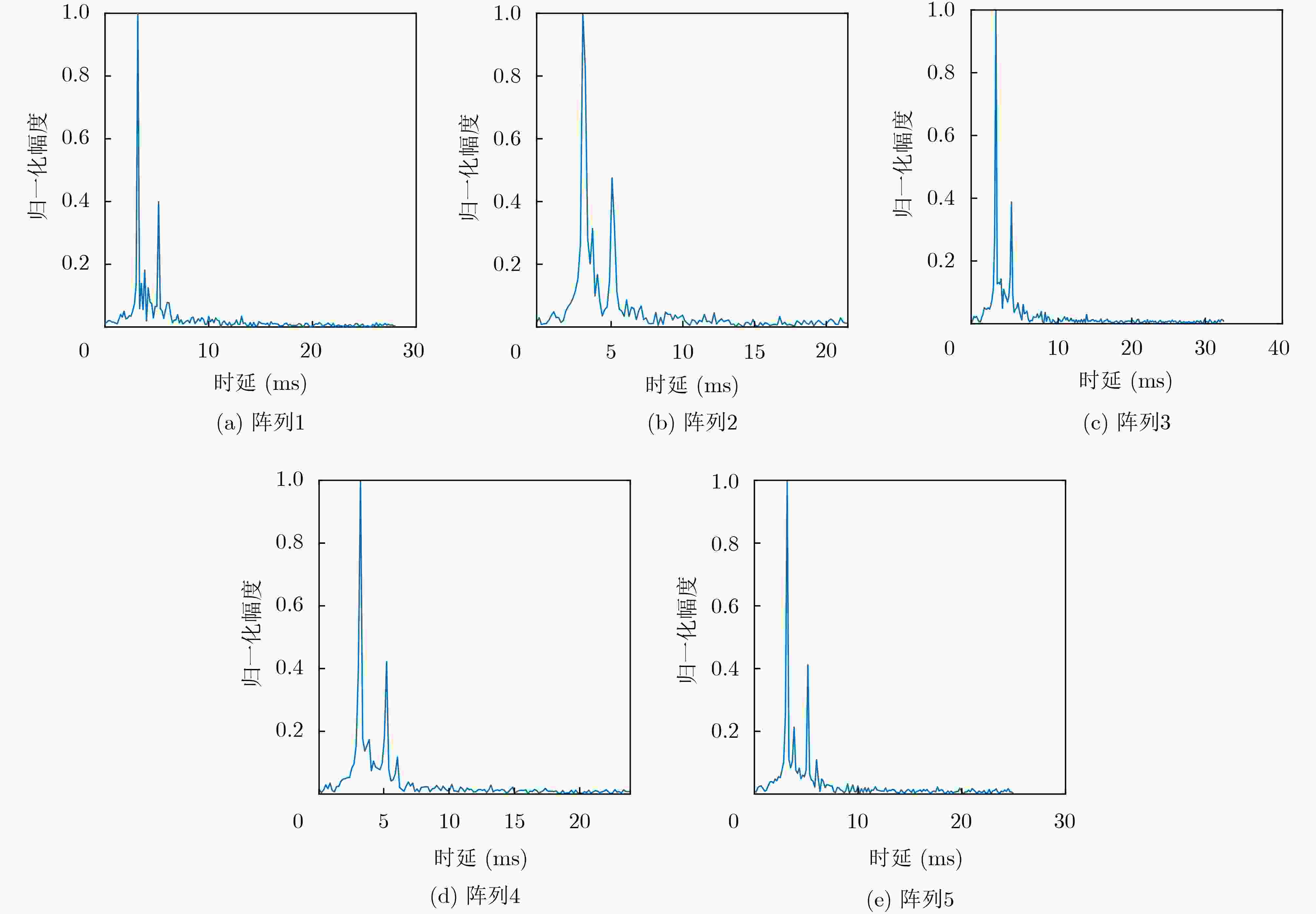
误码率 阵列1 阵列2 阵列3 阵列4 阵列5 本文方法 最大值 0.0568 0.0682 0.0483 0.0710 0.0284 平均值 0.0045 0.0120 0.0049 0.0058 0.0070 OMP-2grid-comp 最大值 0.0625 0.0682 0.0483 0.0739 0.0369 平均值 0.0057 0.0128 0.0063 0.0065 0.0079 OMP-sin 最大值 0.0597 0.0824 0.0540 0.0767 0.0313 平均值 0.0053 0.0146 0.0062 0.0077 0.0080 SdMP 最大值 0.0568 0.0710 0.0597 0.0795 0.0426 平均值 0.0053 0.0127 0.0072 0.0082 0.0079 OMP-normal-comp-8 最大值 0.0568 0.0795 0.0597 0.0824 0.0426 平均值 0.0054 0.0159 0.0067 0.0084 0.0100 -
COATELAN S and GLAVIEUX A. Design and test of a multicarrier transmission system on the shallow water acoustic channel[C]. OCEANS’94, Brest, France, 1994: 472–477. doi: 10.1109/oceans.1994.364244. ZHENG Beixiong and ZHANG Rui. Intelligent reflecting surface-enhanced OFDM: Channel estimation and reflection optimization[J]. IEEE Wireless Communications Letters, 2020, 9(4): 518–522. doi: 10.1109/LWC.2019.2961357 张颖, 姚雨丰. 基于快速贝叶斯匹配追踪优化的海上稀疏信道估计方法[J]. 电子与信息学报, 2020, 42(2): 534–540. doi: 10.11999/JEIT190102ZHANG Ying and YAO Yufeng. Channel estimation algorithm of maritime sparse channel based on fast Bayesian matching pursuit optimization[J]. Journal of Electronics &Information Technology, 2020, 42(2): 534–540. doi: 10.11999/JEIT190102 BERGER C R, ZHOU Shengli, PREISIG J C, et al. Sparse channel estimation for multicarrier underwater acoustic communication: From subspace methods to compressed sensing[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1708–1721. doi: 10.1109/tsp.2009.2038424 GÓMEZ-CUBA F and GOLDSMITH A J. Compressed sensing channel estimation for OFDM with Non-Gaussian multipath gains[J]. IEEE Transactions on Wireless Communications, 2020, 19(1): 47–61. doi: 10.1109/TWC.2019.2941192 WANG Shuche, HE Zhiqiang, NIU Kai, et al. New results on joint channel and impulsive noise estimation and tracking in underwater acoustic OFDM systems[J]. IEEE Transactions on Wireless Communications, 2020, 19(4): 2601–2612. doi: 10.1109/TWC.2020.2966622 TROPP J A and GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655–4666. doi: 10.1109/tit.2007.909108 QIAO Gang, SONG Qingjun, MA Lu, et al. A low-complexity orthogonal matching pursuit based channel estimation method for time-varying underwater acoustic OFDM systems[J]. Applied Acoustics, 2019, 148: 246–250. doi: 10.1016/j.apacoust.2018.12.026 CHI Yuejie, SCHARF L L, PEZESHKI A, et al. Sensitivity to basis mismatch in compressed sensing[J]. IEEE Transactions on Signal Processing, 2011, 59(5): 2182–2195. doi: 10.1109/TSP.2011.2112650 TAUBOCK G, HLAWATSCH F, EIWEN D, et al. Compressive estimation of doubly selective channels in multicarrier systems: Leakage effects and sparsity-enhancing processing[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 255–271. doi: 10.1109/jstsp.2010.2042410 BERGER C R, WANG Zhaohui, HUANG Jianzhong, et al. Application of compressive sensing to sparse channel estimation[J]. IEEE Communications Magazine, 2010, 48(11): 164–174. doi: 10.1109/MCOM.2010.5621984 PANAYIRCI E, ALTABBAA M T, UYSAL M, et al. Sparse channel estimation for OFDM-based underwater acoustic systems in Rician fading with a new OMP-MAP algorithm[J]. IEEE Transactions on Signal Processing, 2019, 67(6): 1550–1565. doi: 10.1109/tsp.2019.2893841 ZENG Wenjun, JIANG Xue, LI Xilin, et al. Deconvolution of sparse underwater acoustic multipath channel with a large time-delay spread[J]. The Journal of the Acoustical Society of America, 2010, 127(2): 909–919. doi: 10.1121/1.3278604 QIAO Gang, SONG Qingjun, MA Lu, et al. Sparse Bayesian learning for channel estimation in time-varying underwater acoustic OFDM communication[J]. IEEE Access, 2018, 6: 56675–56684. doi: 10.1109/access.2018.2873406 UWAECHIA A N and MAHYUDDIN N M. Stage-determined matching pursuit for sparse channel estimation in OFDM systems[J]. IEEE Systems Journal, 2019, 13(3): 2240–2251. doi: 10.1109/JSYST.2018.2837353 WAN Lei, QIANG Xizhu, MA Lu, et al. Accurate and efficient path delay estimation in OMP based sparse channel estimation for OFDM with equispaced pilots[J]. IEEE Wireless Communications Letters, 2019, 8(1): 117–120. doi: 10.1109/LWC.2018.2860996 DRAPER N R and SMITH H. Applied Regression Analysis[M]. 3rd ed. New York: John Wiley & Sons, 1998: 115–134. doi: 10.1002/9781118625590. QIAO Gang, QIANG Xizhu, WAN Lei, et al. Chirp Z-transform based sparse channel estimation for underwater acoustic OFDM in clustered channels[C]. The OCEANS 2018 MTS/IEEE Charleston, Charleston, USA, 2018: 1–6. doi: 10.1109/oceans.2018.8604692. WAN Lei, JIA Hanbo, ZHOU Feng, et al. Fine Doppler scale estimations for an underwater acoustic CP-OFDM system[J]. Signal Processing, 2020, 170: 107439. doi: 10.1016/j.sigpro.2019.107439 KALBAT F, Al-DWEIK A, SHARIF B, et al. Performance analysis of precoded wireless OFDM with carrier frequency offset[J]. IEEE Systems Journal, 2020, 14(2): 2237–2248. doi: 10.1109/JSYST.2019.2922098 -





 下载:
下载:


 下载:
下载:
