Deconvolution-based Target Echo High-resolution Time Delay Estimation Technique Using Active Sonar
-
摘要: 为提高浅海复杂海洋环境下的目标回波时延估计精度,增强主动声呐系统对目标的探测能力,该文基于稀疏表示理论和解卷积思想,提出一种高分辨目标回波时延估计技术。首先,引入Toeplitz算子,将发射信号的不同时延结果构造成时延字典矩阵,时延估计值存在于所求解的稀疏向量中。其次,利用交替方向乘子算法(ADMM)优化框架,求解全局最优解。最后,采用一种加权迭代策略设置正则化参数,进一步抑制多途信道的影响,解耦合出回波到达的时刻,获得高精度的目标回波时延估计结果。数值仿真和实验数据表明,该文提出的解卷积主动声呐目标回波高分辨时延估计技术可以在多途扩展严重的浅海声信道实现目标探测,在信道水池的实验环境下,时延估计分辨率可达0.056 ms。Abstract: In view of enhancing the time delay estimation resolution for the target echo in a complex shallow-water environment, thus improving the target detection ability of the active sonar system. A high-resolution time delay estimation technique is proposed to detect the underwater target based on sparse representation theory and deconvolution framework. Firstly, the Toeplitz operator is introduced here to construct a dictionary matrix using the various time delayed replicing of the transmitting signal. The estimated time-delay value can be found in the desired sparse vector solution. Secondly, the Alternating Direction Method of Multipliers (ADMM) is implemented to calculate the optimal solution globally. Thirdly, the reweighted iteration approach is explored to control the regularization parameter, thus suppressing the impact of the multipath channel. The arrival time of the echo can be decoupled to obtain a high-resolution time delay result. The simulated and experimental data verify that the proposed deconvolution-based time delay estimation technique can be used to detect the underwater target in shallow-water acoustic multipath channels. The resolution of the estimated time-delay result can achieve 0.056 ms.
-
表 1 解卷积时延估计方法流程
输入:接收信号$r$,主动声呐发射信号$s$,正则化系数初值${\lambda ^0}$ 输出:广义信道冲激响应的估计值${\hat{ H}}$ (1) 利用主动声呐发射信号$s$和式(10)构造字典矩阵${{T}}(s)$; (2) 令${\hat{ H}}$为零向量,利用式(23)得到首次迭代时的正则化系数${\lambda ^1}$; (3) 利用式(20)求解ADMM算法中的第1个变量${{x}}$; (4) 利用式(22)求解ADMM算法中的第2个变量${{z}}$,也就是${\hat{ H}}$; (5) 利用式(19)求解ADMM算法中的第3个变量${{u}}$; (6) 将得到的${\hat{ H}}$代入到式(23)中,得到下一次迭代时的正则化系数${\lambda ^\ell }$; (7) 重复步骤3—步骤6,直至达到ADMM算法的迭代停止条件。 表 2 发射信号为线性调频信号,时延估计分辨率(SNR=5 dB)
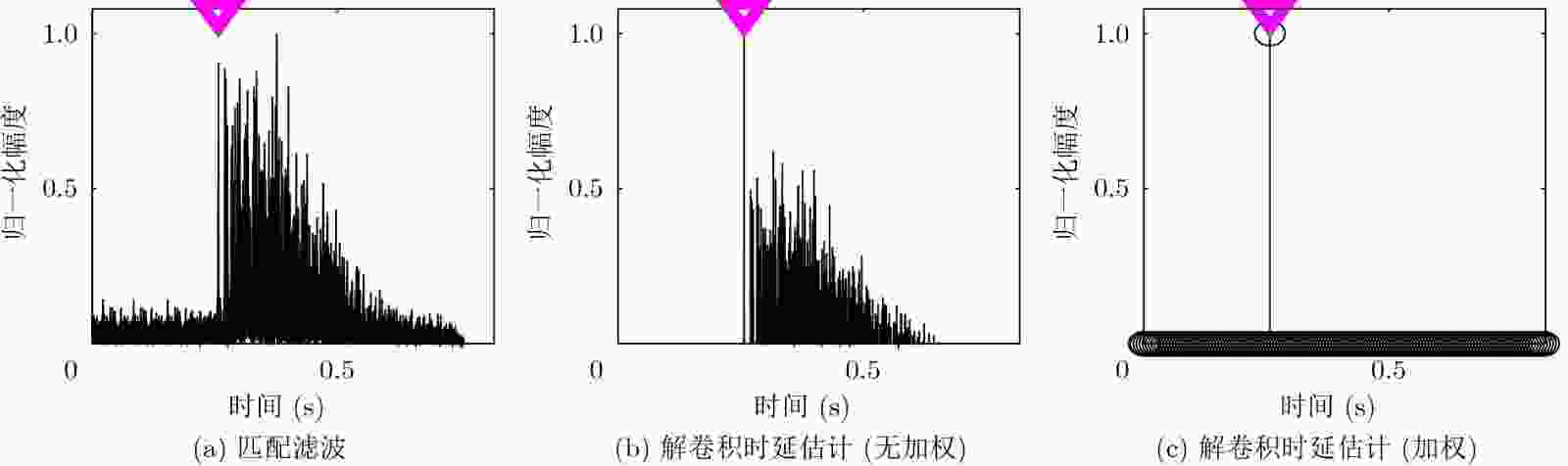
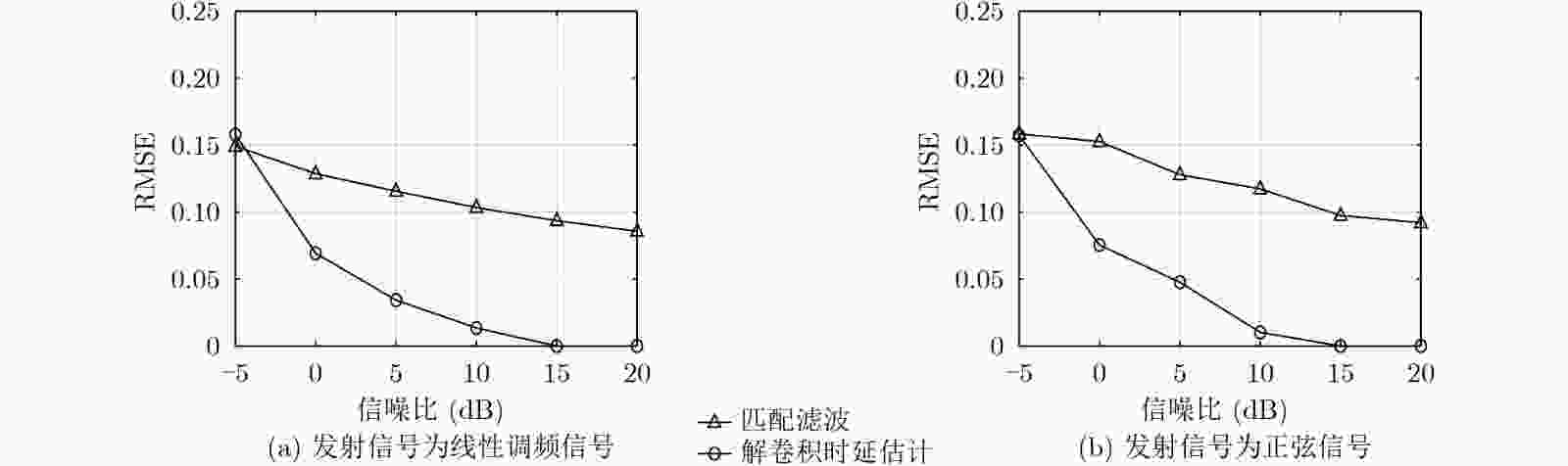
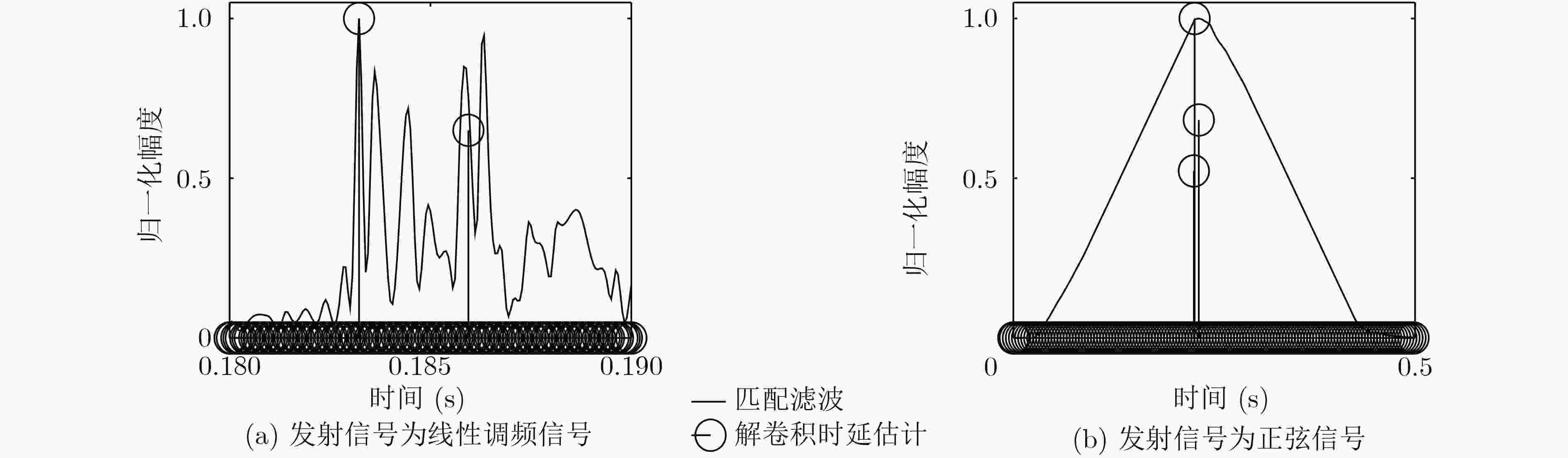
匹配滤波 解卷积时延估计 –3 dB主瓣宽度所占据的平均采样点数 8.230 1.000 时延估计分辨率(ms) 0.514 0.063 表 3 发射信号为正弦信号,时延估计分辨率(SNR=5 dB)
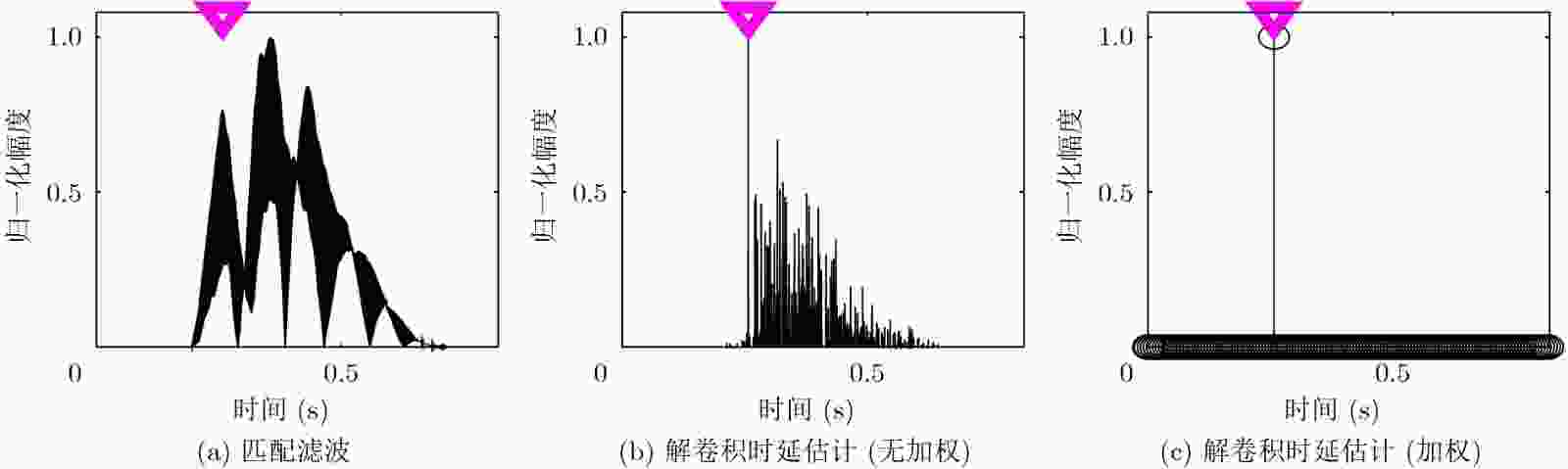
匹配滤波 解卷积时延估计 –3 dB主瓣宽度所占据的平均采样点数 589.500 1.000 时延估计分辨率(ms) 36.300 0.063 -
HAGUE D A and BUCK J R. An experimental evaluation of the generalized sinusoidal frequency modulated waveform for active sonar systems[J]. The Journal of the Acoustical Society of America, 2019, 145(6): 3741–3755. doi: 10.1121/1.5113581 YIN Jingwei, MEN Wei, HAN Xiao, et al. Integrated waveform for continuous active sonar detection and communication[J]. IET Radar, Sonar & Navigation, 2020, 14(9): 1382–1390. doi: 10.1049/iet-rsn.2020.0099 ZHANG Ting, YANG T C, and XU Wen. Bistatic localization of objects in very shallow water[J]. IEEE Access, 2019, 7: 180640–180651. doi: 10.1109/ACCESS.2019.2947851 YANG T C. Deconvolved conventional beamforming for a horizontal line array[J]. IEEE Journal of Oceanic Engineering, 2018, 43(1): 160–172. doi: 10.1109/JOE.2017.2680818 MA Lin, GULLIVER T A, ZHAO Anbang, et al. Underwater broadband source detection using an acoustic vector sensor with an adaptive passive matched filter[J]. Applied Acoustics, 2019, 148: 162–174. doi: 10.1016/j.apacoust.2018.12.023 HAMA Y and OCHIAI H. Performance analysis of matched-filter detector for MIMO spatial multiplexing over rayleigh fading channels with imperfect channel estimation[J]. IEEE Transactions on Communications, 2019, 67(5): 3220–3233. doi: 10.1109/TCOMM.2019.2892758 PADOIS T, DOUTRES O, and SGARD F. On the use of modified phase transform weighting functions for acoustic imaging with the generalized cross correlation[J]. The Journal of the Acoustical Society of America, 2019, 145(3): 1546–1555. doi: 10.1121/1.5094419 CHANDRAN V, ELGAR S, and NGUYEN A. Detection of mines in acoustic images using higher order spectral features[J]. IEEE Journal of Oceanic Engineering, 2002, 27(3): 610–618. doi: 10.1109/JOE.2002.1040943 BENESTY J, CHEN Jingdong, and HUANG Yiteng. Time-delay estimation via linear interpolation and cross correlation[J]. IEEE Transactions on Speech and Audio Processing, 2004, 12(5): 509–519. doi: 10.1109/TSA.2004.833008 SALVATI D and CANAZZA S. Adaptive time delay estimation using filter length constraints for source localization in reverberant acoustic environments[J]. IEEE Signal Processing Letters, 2013, 20(5): 507–510. doi: 10.1109/LSP.2013.2253319 SHAO Zhenfeng, WANG Lei, WANG Zhongyuan, et al. Remote sensing image super-resolution using sparse representation and coupled sparse autoencoder[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(8): 2663–2674. doi: 10.1109/JSTARS.2019.2925456 崔维嘉, 张鹏, 巴斌. 基于贝叶斯自动相关性确定的稀疏重构正交频分复用信号时延估计算法[J]. 电子与信息学报, 2019, 41(10): 2318–2324. doi: 10.11999/JEIT181181CUI Weijia, ZHANG Peng, and BA Bin. Sparse reconstruction OFDM delay estimation algorithm based on Bayesian automatic relevance determination[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2318–2324. doi: 10.11999/JEIT181181 王洪雁, 于若男. 基于稀疏和低秩恢复的稳健DOA估计方法[J]. 电子与信息学报, 2020, 42(3): 589–596. doi: 10.11999/JEIT190263WANG Hongyan and YU Ruonan. Sparse and low rank recovery based robust DOA estimation method[J]. Journal of Electronics &Information Technology, 2020, 42(3): 589–596. doi: 10.11999/JEIT190263 MENG Xiangxia, LI Xiukun, JAKOBSSON A, et al. Sparse estimation of backscattered echoes from underwater object using integrated dictionaries[J]. The Journal of the Acoustical Society of America, 2018, 144(6): 3475–3484. doi: 10.1121/1.5083830 XIA Zhi, LI Xiukun, and MENG Xiangxia. High resolution time-delay estimation of underwater target geometric scattering[J]. Applied Acoustics, 2016, 114: 111–117. doi: 10.1016/j.apacoust.2016.07.016 HAUPT J, BAJWA W U, RAZ G, et al. Toeplitz compressed sensing matrices with applications to sparse channel estimation[J]. IEEE Transactions on Information Theory, 2010, 56(11): 5862–5875. doi: 10.1109/TIT.2010.2070191 TIBSHIRANI R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society: Series B (Methodological) , 1996, 58(1): 267–288. doi: 10.1111/j.2517-6161.1996.tb02080.x GRANT M and BOYD S. CVX: Matlab software for disciplined convex programming, version 2.1[OL]. http://cvxr.com/, 2014. BOYD S, PARIKH N, CHU E, et al. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers[M]. Boston: Now Publishers Inc., 2011. doi: 10.1561/2200000016. CANDÈS E J, WAKIN M B, and BOYD S P. Enhancing sparsity by reweighted ℓ1 minimization[J]. Journal of Fourier Analysis and Applications, 2008, 14(5/6): 877–905. doi: 10.1007/s00041-008-9045-x -





 下载:
下载:


 下载:
下载:
