Radio Frequency Stealth-based Optimal Radio Frequency Resource Allocation Algorithm for Multiple-target Tracking in Radar Network
-
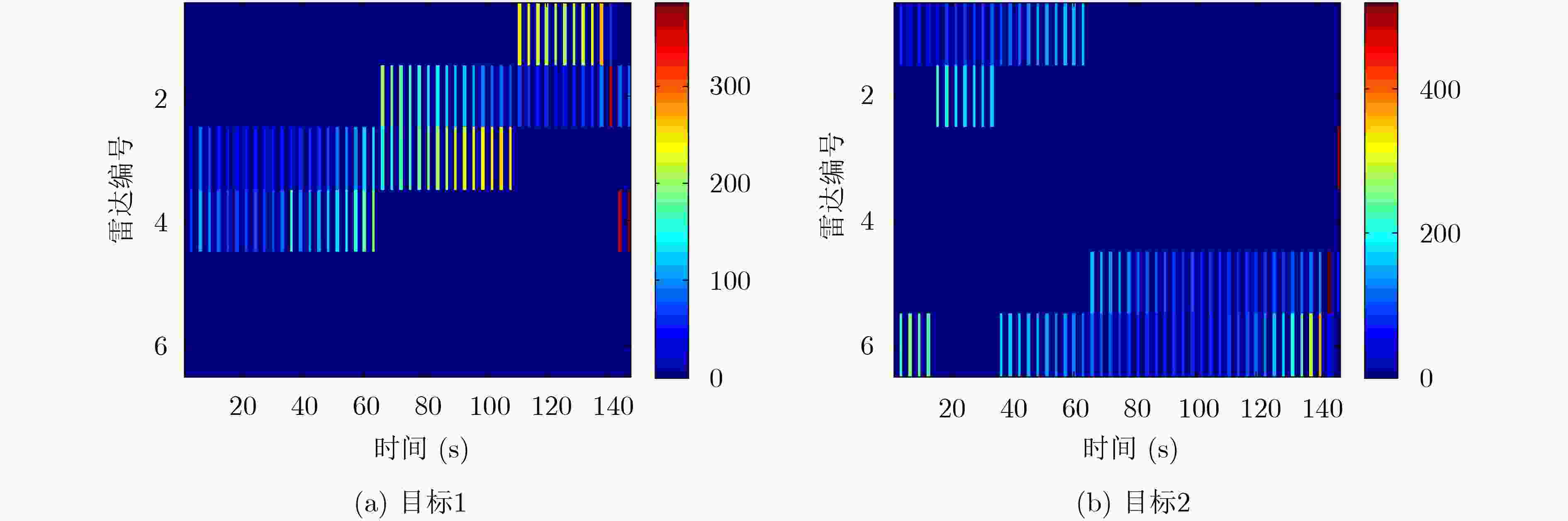
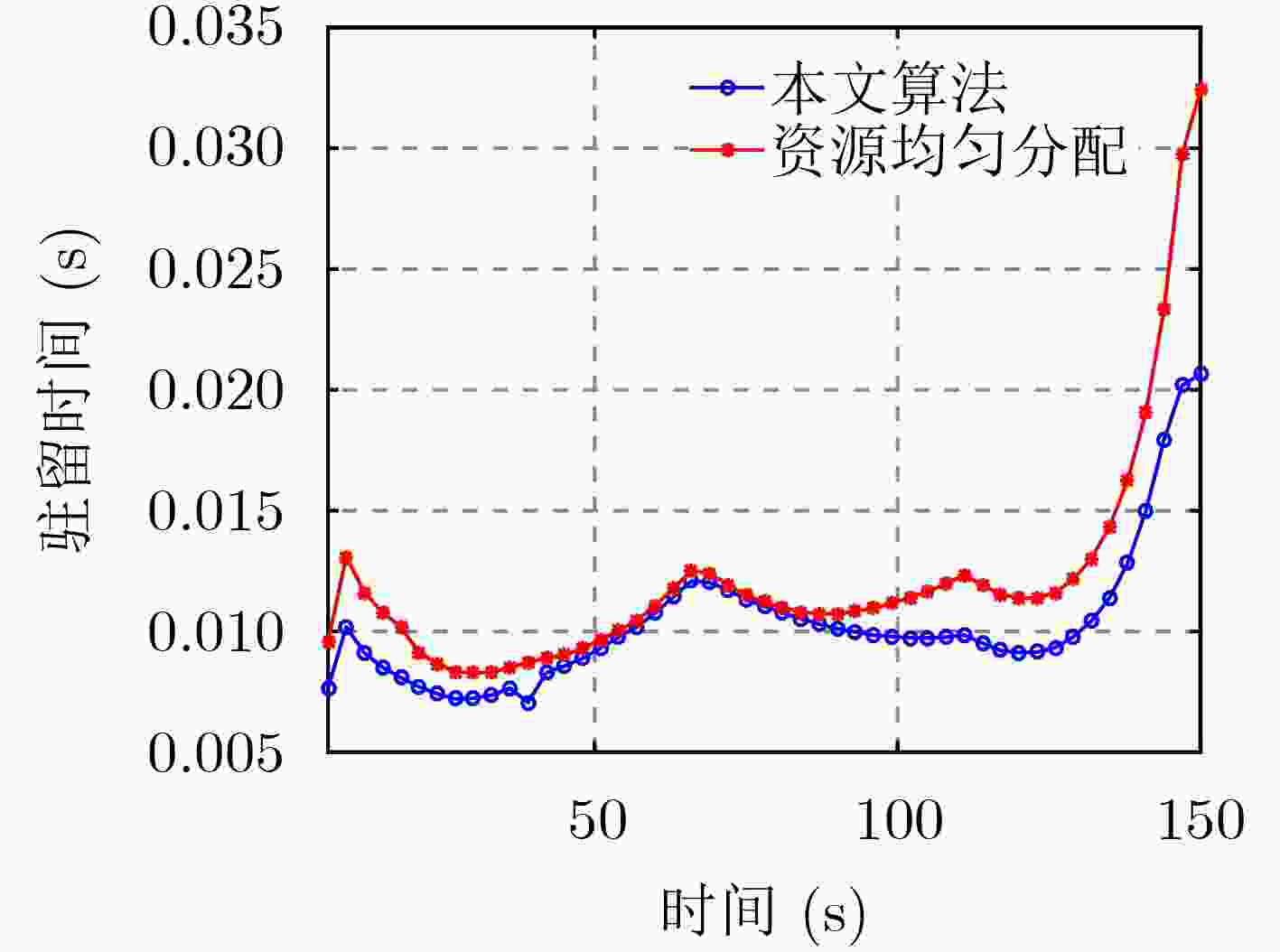
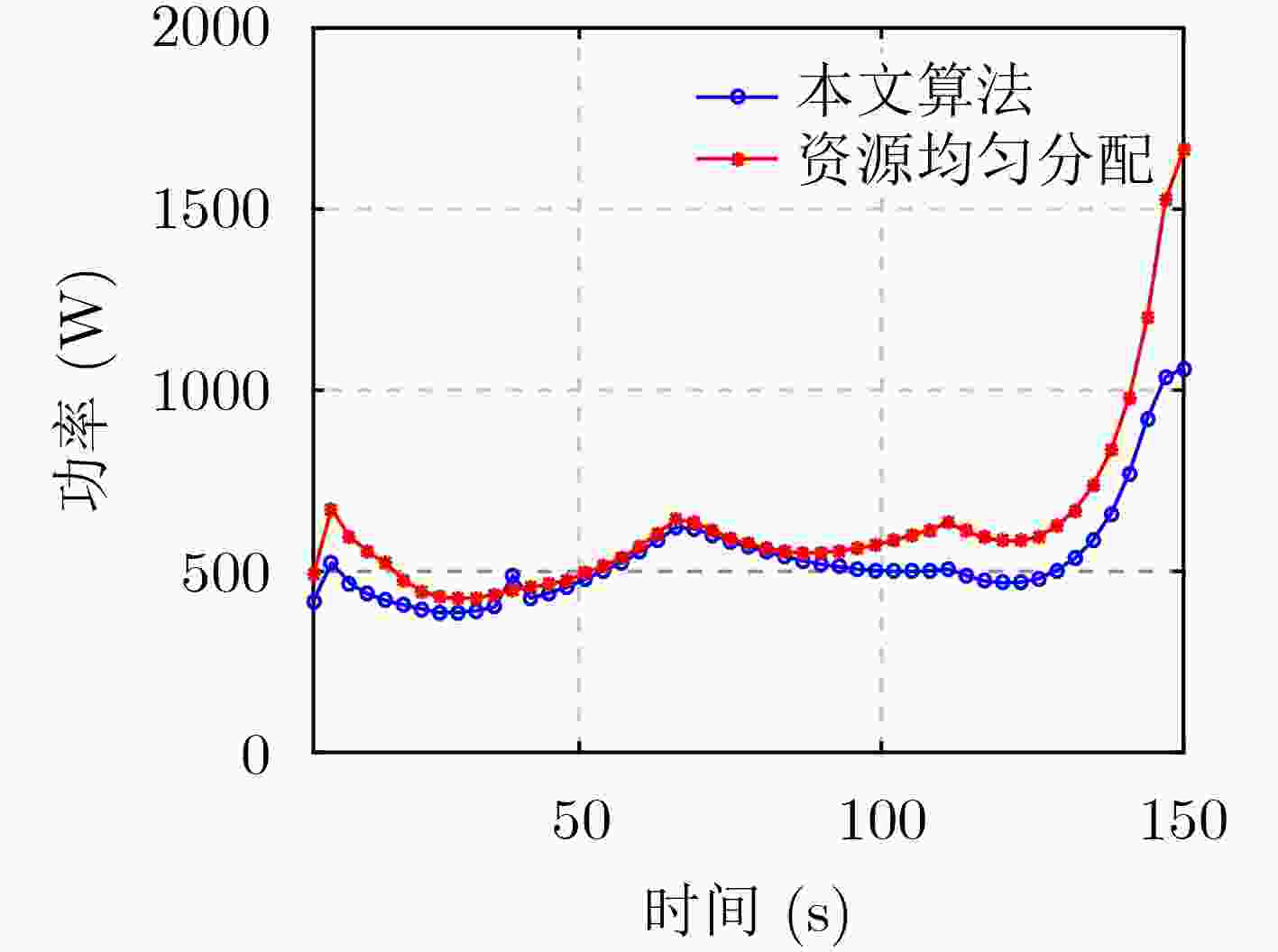
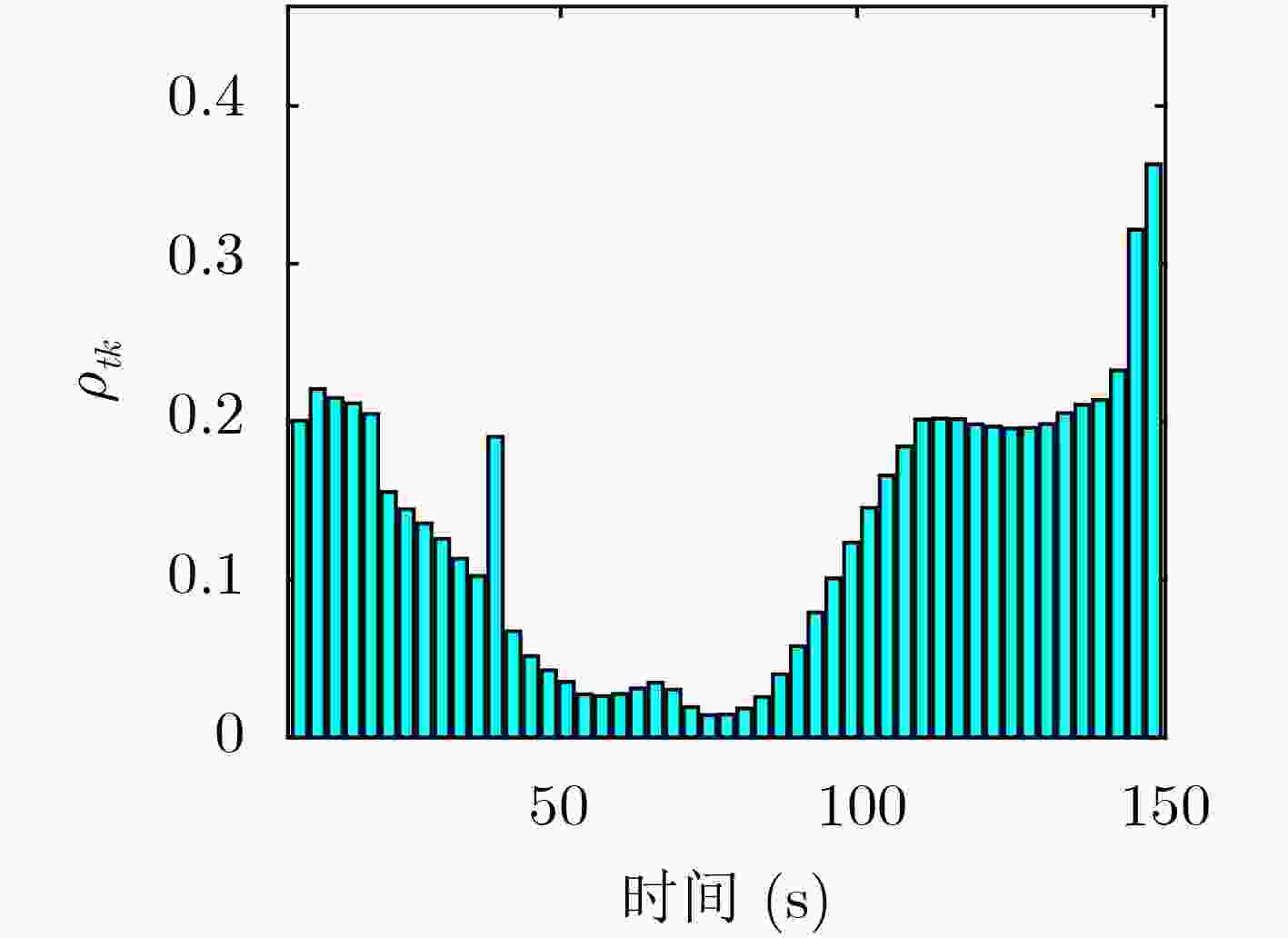
摘要: 针对组网雷达系统多目标跟踪场景,该文提出一种面向射频(RF)隐身的组网雷达射频辐射资源优化分配算法。首先,采用目标跟踪误差的贝叶斯克拉美-罗下界(BCRLB)作为目标跟踪性能指标。其次,以各雷达照射目标的驻留时间资源和辐射功率资源加权和为优化目标,以BCRLB不大于给定目标跟踪精度阈值及系统射频辐射资源作为约束条件,建立了包含雷达节点分配方式、驻留时间和辐射功率3个优化变量的优化模型。然后,采用两步分解法对上述优化模型进行了求解,即先固定雷达节点选择,利用内点法对简化后的非凸非线性优化模型进行求解,之后再通过匈牙利算法确定最佳雷达节点分配方式。仿真结果表明,相较于辐射资源均匀分配算法,所提算法可以有效降低组网雷达的射频资源消耗,提升系统射频隐身性能。Abstract: In the scenario of multi-target tracking by a radar network system, a Radio Frequency (RF) stealth-based optimal RF resource allocation algorithm in radar network is proposed. Firstly, the Bayesian Cramer-Rao Lower Bound (BCRLB) of target tracking error is used as the target tracking performance index. Secondly, the optimization model is established which includes three optimization variables: radar node selection, dwell time and radiation power. In this model, the objective function is the weighted sum of the dwell time resources and radiation power resources of each radar, the constraint condition can be conclude that the BCRLB must be less than the given threshold and the system RF radiation resources must be between the upper and lower limits. Then, the two-step decomposition method is used to solve the above optimization model. The radar node selection is fixed first, then the interior point method is used to solve the simplified non-convex nonlinear optimization model, and then the Hungarian algorithm is used to determine the best radar node selection mode. The simulation results show that compared with uniform resource allocation algorithm, the proposed algorithm can effectively reduce the RF resource consumption of the radar network and improve the RF stealth performance of the system.
-
表 1 固定雷达分配方式的辐射资源优化控制算法
步骤 1 令${g_1} = {\kern 1pt} F_{k\left| {k - 1} \right.}^s - {F_{\max }}$,${g_2} = {\kern 1pt} {T_{{\rm{d,min}}}} - T_{{\rm{d}},1,k}^s$, ${g_3} = {\kern 1pt} {T_{{\rm{d,min}}}} - T_{{\rm{d}},2,k}^s$,···, ${g_{M + 1}} = {T_{{\rm{d,min}}}} - {\kern 1pt} T_{{\rm{d}},M,k}^s$, ${g_{M + 2}} = {\kern 1pt} T_{{\rm{d}},1,k}^s - {T_{{\rm{d,max}}}}$,
${g_{M + 3}} = {\kern 1pt} T_{{\rm{d}},2,k}^s - {T_{{\rm{d,max}}}}$,···, ${g_{2M + 1}} = {\kern 1pt} T_{{\rm{d}},M,k}^s - {T_{{\rm{d,max}}}}$, ${g_{2M + 2}} = {\kern 1pt} {P_{\min }} - P_{1,k}^s$, ${g_{2M + 3}} = {\kern 1pt} {P_{\min }} - P_{2,k}^s$,···, ${g_{3M + 1}} = {\kern 1pt} {P_{\min }} - P_{M,k}^s$,
${g_{3M + 2}} = P_{1,k}^s - {P_{\max }}$,···, ${g_{4M + 1}} = P_{M,k}^s - {P_{\max }}$,设置可行域:$D = \left\{ T_{ {\rm{d} },m,k}^s,P_{m,k}^s\left| {g_a}\left( {T_{ {\rm{d} },m,k}^s,P_{m,k}^s} \right) \le 0,a = 1,2, ··· ,4M + 1,\right.\right.$
$\left.1 \le m \leq M \right\}$其中,${g_a}\left( {T_{{\rm{d}},m,k}^s,P_{m,k}^s} \right) = {g_a},a = 1,2, ··· ,4M + 1$,取${\left( {T_{{\rm{d}},m,k}^s,P_{m,k}^s} \right)^{\left( 0 \right)}} \in D\left( {1 \le m \le M} \right)$为初始点,$\varepsilon > 0$为算法终
止指标,${\xi _1} > 0$, $c \ge 2$,令$l = 1$;
步骤 2 以${\left( {T_{{\rm{d}},m,k}^s,P_{m,k}^s} \right)^{\left( {l - 1} \right)}}$为初始点求解如下子问题:$\min {\kern 1pt} {F_1} - {\xi _1}\left[ {\frac{1}{ { {g_1} } } + \frac{1}{ { {g_2} } } + ··· + \frac{1}{ { {g_{2M + 2} } } } } \right], {\rm{s} }{\rm{.t} }{\rm{.} }{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} T_{ {\rm{d} },m,k}^s,P_{m,k}^s \in D$,其中,${F_1}$表
示式(7)中的优化目标函数,令上述问题的极小值点为${\left( {T_{{\rm{d}},m,k}^s,P_{m,k}^s} \right)^{\left( l \right)}}$;步骤 3 检验终止条件,若$- {\xi _l}\left[ {\dfrac{1}{ { {g_1} } } + \dfrac{1}{ { {g_2} } } + ··· + \dfrac{1}{ { {g_{4M + 1} } } } } \right] < \varepsilon$,算法终止;否则,令${\xi _{l + 1} } \leftarrow \dfrac{ { {\xi _l} } }{c}$, $l \leftarrow l + 1$,转入步骤2。 -
时晨光, 周建江, 汪飞, 等. 机载雷达组网射频隐身技术[M]. 北京: 国防工业出版社, 2019: 3–23.SHI Chenguang, ZHOU Jianjiang, WANG Fei, et al. Radio Frequency Stealth Technology for Airborne Radar Network[M]. Beijing: National Defense Industry Press, 2019: 3–23. 严俊坤, 戴奉周, 秦童, 等. 一种针对目标三维跟踪的多基地雷达系统功率分配算法[J]. 电子与信息学报, 2013, 35(4): 901–907.YAN Junkun, DAI Fengzhou, QIN Tong, et al. A power allocation approach for 3D target tracking in multistatic radar systems[J]. Journal of Electronics &Information Technology, 2013, 35(4): 901–907. 胡捍英, 孙扬, 郑娜娥. 多目标速度估计的分布式MIMO雷达资源分配算法[J]. 电子与信息学报, 2016, 38(10): 2453–2460. doi: 10.11999/JEIT151452HU Hanying, SUN Yang, and ZHENG Nae. Resource allocation approach in distributed MIMO radar with multiple targets for velocity estimation[J]. Journal of Electronics &Information Technology, 2016, 38(10): 2453–2460. doi: 10.11999/JEIT151452 LI Jian and STOICA P. MIMO radar with colocated antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106–114. doi: 10.1109/MSP.2007.904812 FISHLER E, HAIMOVICH A, BLUM R S, et al. Spatial diversity in radars—models and detection performance[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 823–838. doi: 10.1109/TSP.2005.862813 ZHANG Haowei, XIE Junwei, SHI Junpeng, et al. Sensor scheduling and resource allocation in distributed MIMO radar for joint target tracking and detection[J]. IEEE Access, 2019, 7: 62387–62400. doi: 10.1109/ACCESS.2019.2916334 CHAVALI P and NEHORAI A. Scheduling and power allocation in a cognitive radar network for multiple-target tracking[J]. IEEE Transactions on Signal Processing, 2012, 60(2): 715–729. doi: 10.1109/TSP.2011.2174989 CHEN Haowen, TA Shiying, and SUN Bin. Cooperative game approach to power allocation for target tracking in distributed MIMO radar sensor networks[J]. IEEE Sensors Journal, 2015, 15(10): 5423–5432. doi: 10.1109/JSEN.2015.2431261 GODRICH H, PETROPULU A P, and POOR H V. Power allocation strategies for target localization in distributed multiple-radar architectures[J]. IEEE Transactions on Signal Processing, 2011, 59(7): 3226–3240. doi: 10.1109/TSP.2011.2144976 严俊坤, 纠博, 刘宏伟, 等. 一种针对多目标跟踪的多基雷达系统聚类与功率联合分配算法[J]. 电子与信息学报, 2013, 35(8): 1875–1881.YAN Junkun, JIU Bo, LIU Hongwei, et al. Joint cluster and power allocation algorithm for multiple targets tracking in multistatic radar systems[J]. Journal of Electronics &Information Technology, 2013, 35(8): 1875–1881. 李正杰, 谢军伟, 张浩为, 等. 基于集中式MIMO雷达的多目标跟踪功率分配优化算法[J]. 空军工程大学学报(自然科学版), 2019, 20(5): 76–82.LI Zhengjie, XIE Junwei, ZHANG Haowei, et al. Multiple targets tracking power allocation optimization algorithm based on collocated MIMO radar[J]. Journal of Air Force Engineering University (Natural Science Edition) , 2019, 20(5): 76–82. ZHANG Haowei, ZONG Binfeng, and XIE Junwei. Power and bandwidth allocation for multi-target tracking in collocated MIMO radar[J]. IEEE Transactions on Vehicular Technology, 2020, 69(9): 9795–9806. doi: 10.1109/TVT.2020.3002899 LI Zhengjie, XIE Junwei, ZHANG Haowei, et al. Adaptive sensor scheduling and resource allocation in netted collocated MIMO radar system for multi-target tracking[J]. IEEE Access, 2020, 8: 109976–109988. doi: 10.1109/ACCESS.2020.3001358 YAN Junkun, PU Wenqiang, ZHOU Shenghua, et al. Optimal resource allocation for asynchronous multiple targets tracking in heterogeneous radar networks[J]. IEEE Transactions on Signal Processing, 2020, 68: 4055–4068. doi: 10.1109/TSP.2020.3007313 YI Wei, YUAN Ye, HOSEINNEZHAD R, et al. Resource scheduling for distributed multi-target tracking in netted colocated MIMO radar systems[J]. IEEE Transactions on Signal Processing, 2020, 68: 1602–1617. doi: 10.1109/TSP.2020.2976587 YUAN Ye, YI Wei, KIRUBARAJAN T, et al. Scaled accuracy based power allocation for multi-target tracking with colocated MIMO radars[J]. Signal Processing, 2019, 158: 227–240. DAI Jinhui, YAN Junkun, WANG Penghui, et al. Optimal resource allocation for multiple target tracking in phased array radar network[C]. 2019 International Conference on Control, Automation and Information Sciences (ICCAIS), Chengdu, China, 2019: 1–4. doi: 10.1109/ICCAIS46528.2019.9074602. DING Lintao, SHI Chenguang, QIU Wei, et al. Joint dwell time and bandwidth optimization for multi-target tracking in radar network based on low probability of intercept[J]. Sensors, 2020, 20(5): 1269. doi: 10.3390/s20051269 SHI Chenguang, DING Lintao, WANG Fei, et al. Low probability of intercept-based collaborative power and bandwidth allocation strategy for multi-target tracking in distributed radar network system[J]. IEEE Sensors Journal, 2020, 20(12): 6367–6377. doi: 10.1109/JSEN.2020.2977328 LAWRENCE D E. Low probability of intercept antenna array beamforming[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(9): 2858–2865. doi: 10.1109/TAP.2010.2052573 SHI Chenguang, WANG Fei, SELLATHURAI M, et al. Power minimization-based robust OFDM radar waveform design for radar and communication systems in coexistence[J]. IEEE Transactions on Signal Processing, 2018, 66(5): 1316–1330. doi: 10.1109/TSP.2017.2770086 BOYD S and VANDENBERGHE L. Convex Optimization[M]. Cambridge: Cambridge University Press, 2004: 297–301. -





 下载:
下载:


 下载:
下载:
